大神也会猜错:那些错误的数学猜想
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
作者, SAMUEL ARBESMAN ,此文原载于WIRED网站。
翻译,donkeycn,哆嗒数学网翻译组成员,华东师范大学数学博士。
众所周知地,我们的直觉并不总是完美的。在日常生活中相当多的方面,可以预见的是我们理性的力量是不够强大的。当我们遇到稍微深奥一点的事情时,我们又能做什么呢?我们使用我们的理性——我们的能力来做推断和预测,最终却依然可能会失败,原因很简单:因为事情往往太复杂了。这种情况似乎体现在我最近在 Quora(译者注:一个问答SNS网站)上碰到的一个问题:有哪些猜想是因为一些“非常大的数字”的反例,从而导致它被证明是错误的?
从本质上讲,提问者感兴趣的是如下情况:有哪些数学猜想刚被提出来时看上去是对的,但是推翻它反例却远远超出人类本身的计算能力,只能用先进的应用程序来证明它是错误的。
这样的情况有很多。一个比较著名的例子是波利亚猜想。这个猜想说的是:给定一个正整数N(译者注:N≥2),所有不超过N的正整数中,有偶数个素因子(译者注:素因子数按重数计算,1的素因子数定义为0,)的数不超过有奇数个素因子的数。直到当你检验906150257这个数之前,这看起来都是对的。但是我们的感觉错了。
另一个例子来自欧拉猜想:
十七世纪瑞士数学家莱昂哈德-欧拉声称如下方程就像费马大定理中的方程一样没有正整数解:

二百年来,没有人能证明欧拉猜想,但另一方面,也没有人能找出一个反例来否定它。首先是人工搜索,然后是多年的计算机筛选都未能找到一个解。没有找到反例是这个猜想成立的强有力的证据。然而在1988年,哈佛大学的 Noam Elkies 发现以下这个解:
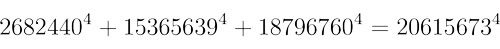
尽管二百年来都没有找到反例,但最终欧拉猜想被证明是错的。事实上,Noam Elkies 证明了这个方程有无穷多个解。
正如 Singh 所注的(译者注:此处指 Simon Singh 及其所著的《费马大定理:一个困惑了世间智者358年的谜》):“这里的教训是,你不能通过只对前一百万个数字来证明一个猜想对所有的数都成立。”
这些实例是迷人的。他们表明,再大的数字也不是无穷大,故而并不能成为证明。我们人类的大脑是强大的,但我们必须更多地与机器的合作,以帮助我们突破我们直觉的束缚。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

写的真好 祝越来越好