选出你心中最美的公式
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
原文作者:Melissa Hogenboom,此文原载于BBC地球频道的网站上。
译文作者:我是崔小白,哆嗒数学网翻译组成员,就读于中国矿业大学。
我们邀请了一组数学家和物理学家,询问他们最喜欢的公式。
现在你也可以选出你觉得最好的那个。
数理方程蕴含着诸多美妙之处,他们代表了宇宙万物的真理。
需要多年的学习才能理解这些深奥的公式,其中很多公式过于复杂以至于很难用普通的语言来表述,但这并影响我们欣赏他们的美妙之处。
英国广播公司地球频道(BBC Earth)邀请了物理学家和数学家,询问他们认为最美丽的公式。他们的回答范围包含了从反物质的解释到亚原子粒子行为的预测。
请浏览下面的12个公式,为你最喜欢的方程投上一票。
(1)狄拉克方程
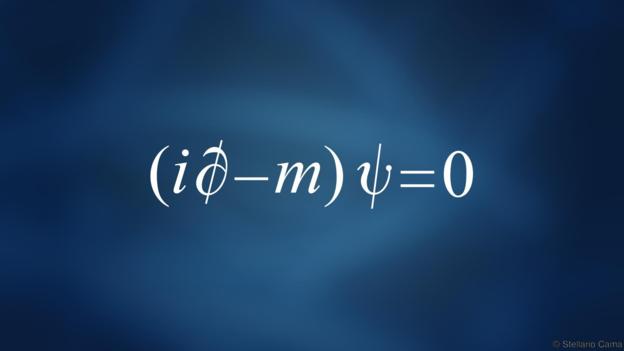
(一个方程汇集了现代物理学的两大基石:量子力学和相对论)
“它的美在于优雅和简洁”,英国吉尔福德萨里大学的吉姆•艾尔-卡利里(Jim Al-Khalili)说:“这个方程的强大之处在于它在20世纪物理学史上的意义和作用。”
该方程是在20世纪20年代末由物理学家狄拉克发现,迄今仍极具影响力。
它汇集了两个最重要的科学思想:描述微观物体特性的量子力学和描述高速运动物体特性的爱因斯坦狭义相对论。这样一来,狄拉克方程便可以描述诸如电子这样的粒子在接近光速时的特性。
卡利里说:“它是量子场论的第一步,可以给出粒子物理学的标准模型以及希格斯玻色子。”
英国伦敦大学学院的物理学家乔恩•巴特沃斯(Jon Butterworth)也选择了狄拉克方程。
“我喜爱狄拉克方程,因为它将优雅的数学与的影响力巨大的物理结合起来,”巴特沃斯说,“保罗•狄拉克决心要找出一个适合于电子运动的相对论性量子方程。他不但做到了而且影响更为深远,因为任何人都可以有梦想。”
也许最重要的是,狄拉克方程预言了反物质(所有已知粒子的镜像)的存在。随后反物质在现实世界中被发现。
“对于一个方程而言很不错”,巴特沃斯说到。
(2)黎曼公式
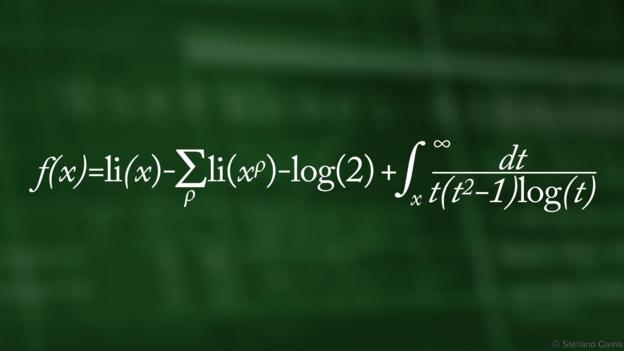
(伯恩哈德•黎曼的公式解开了素数的秘密)
“素数就像是数字的原子”,马库斯•杜•索托伊说:“他们是世界上最基本和最重要的数字。但令人惊讶的是,尽管研究了2000多年,我们仍然不能彻底理解他们。”
素数是只能被1和它本身整除的数。例如3是一个素数而8不是,因为8可以被2和4整除。
数学家伯恩哈德•黎曼在1859年发表了这个公式。它允许你计算出在给定范围内素数的个数。例如黎曼公式表明,在1和100之间有25个素数。
黎曼公式表明素数是由一种叫做ζ函数控制的,“乍一看与素数无关”,杜•索托伊说到。
“对我来说这个方程具备了一个优秀数学的重要特征:它讲述了一个故事”,他说:“从方程描述素数的一侧转换到零点控制的另一侧,就像发现了一个连接两部分数学世界的秘密通道,没有人会认为彼此有任何关系。
这个方程意味着素数存在着更深层次的规律。“数学家现在正花时间尝试理解似乎是这些零点最为核心的规律”,杜•索托伊说到。
素数具有重大的现实意义,因为大多数加密算法依赖于他们。“当今互联网所有的密码利用素数来保证信息传输的安全”,杜•索托伊说:“解开素数的奥秘就等于解开了所有密码的奥秘。”
(3)圆周率π
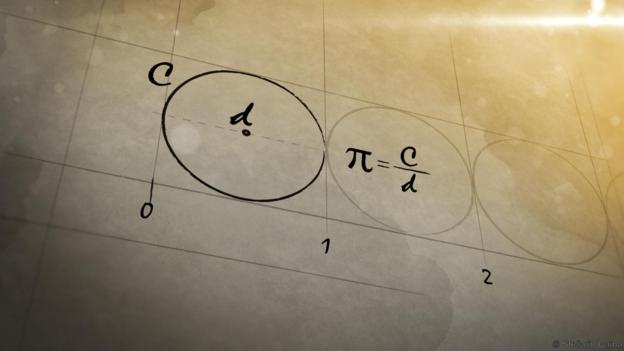
(π是宇宙中最重要的数字之一)
“我对我的学生说如果这个公式不能完全震撼到他们,只能说明他们根本就没有灵魂”,英国巴斯大学的克利斯•巴德(Chris Budd)说。
许多读者都听说过这个著名的公式。它只是描述了一个圆的周长是如何随着直径的变化而变化的。两者的比值是一个数称为π。它是大约3.14,但不精确:π是一个无理数,意味着其小数是永远不循环的。
“π是一个非常重要的数字,”巴德说。”我们在计算诸如GPS等对计算精度要求相当高的现代技术时必然会使用它…它可以用来描述世界的几何形状。
(4)欧拉-拉格朗日方程
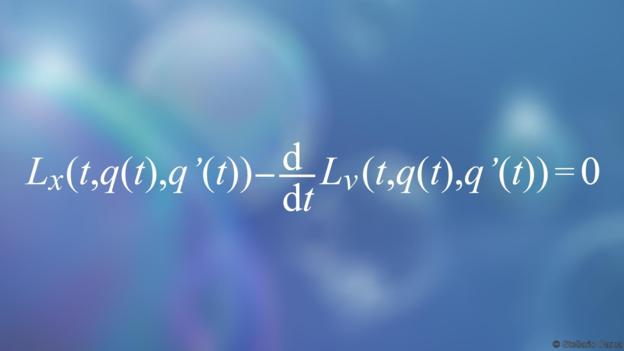
(除此之外,该方程可以描述一个火箭围绕黑洞运行的轨迹)
这个方程可以用于分析从肥皂泡的形状到火箭在黑洞周围的轨迹的所有问题。
“它不仅仅是一个方程,实际上是一个可以产生无限多种可能的物理定律”,伦敦大学学院的安德鲁•波岑(Andrew Pontzen)说。
尽管其应用广泛,但方程却“看似简短”,波岑说:“在一个单一的框架内,所有的经典物理表达和理解方式,都有助于揭示看似不同的现象之间的深层联系。”
(5)杨-巴克斯特方程
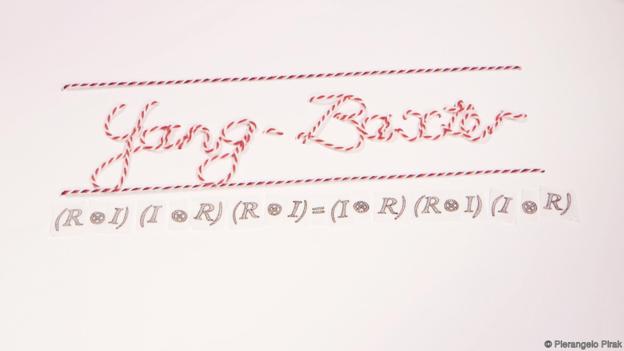
( 该方程阐述了数学中的纽结理论)
“杨-巴克斯特方程是一个简单的方程,简单到可以用一个两岁小孩画出的画来阐释”。英国爱丁堡赫瑞瓦特大学的罗伯特•韦斯顿(Robert Weston)说到。
就像欧拉-拉格朗日方程那样,虽然看似简单但是对数学和物理的许多领域有着深远的影响。其中包括浅水波的特性,亚原子粒子间的相互作用,纽结理论和弦理论。“你可以想象它是蜘蛛网的中心,”韦斯顿说,“在链路上你可以找到许多主题,而它则发挥着基础性作用。”
该方程表面上看起来和这些主题毫无联系,而这也正是吸引韦斯顿的地方。
“每天我都很惊讶,有时候甚至很困惑,具体的物理体系会被过去50年发展起来的一些非常抽象的数学结构所恰当的描述,而且我感到惊讶的是人们已经完全做到了这一点。”
(6)欧拉公式
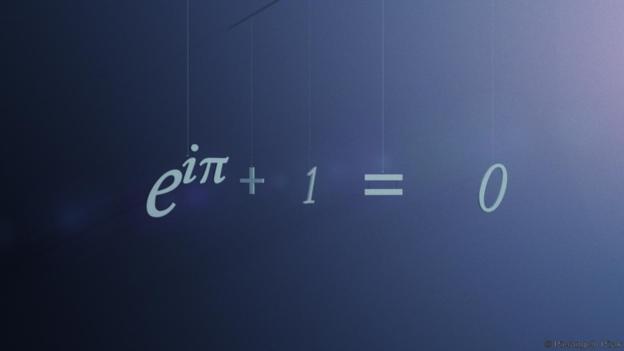
(欧拉被人称为“数学界的莫扎特”,其最著名的方程将所有最重要的数字联系在一起。)
“大多数现代数学和物理学起源于莱昂哈德•欧拉的工作,”英国开放大学的罗宾•威尔逊说,他是“最多产的数学家”和“数学的莫扎特”。但是他的成就,“许多所谓受过教育的人从来没有听说过他。”
他最著名的公式是欧拉恒等式,被称作是可以连接所有数学常数的公式。
该公式将数学中最重要的五个数字组合在一起:
他们是:
●1 – 其他数字的基础
●0 – 虚无的概念
●π – 定义圆的数字
●e – 指数增长的底数
●i – 虚构出的-1的平方根
数字都有许多实际应用,包括通讯、导航、能源、制造、金融、气象、医学。但这不是全部。欧拉公式也包含三个最基本的数学运算:加法,乘法和乘方。
“欧拉公式令人不可思议,因为它看起来简单但是内涵极为丰富。这个公式更吸引我的地方在于,它以一种非常简洁的方式将一些复杂并且看起来不相关的概念结合在一起”,英国索尔福德大学的大卫•珀西(David Percy)说到,他不能在欧拉公式和贝叶斯公式之间做出一个选择。
(7)贝叶斯公式

(这个公式可以让你计算出事件发生的概率)
这个方程由托马斯•贝叶斯牧师在18世纪首次提出。它可以计算事件B发生的情况下事件A发生的概率。
它被用于许多用途,包括检测故障,监视,军事国防,搜索和救援行动,医疗检查,甚至是垃圾邮件过滤器。
“它的美是因为它基于理性思考和决策,而不是因为任何内在的美感”,英国索尔福德大学大卫•珀西说,他不能够在贝叶斯公式和欧拉公式做出一个选择。
(8)波动方程
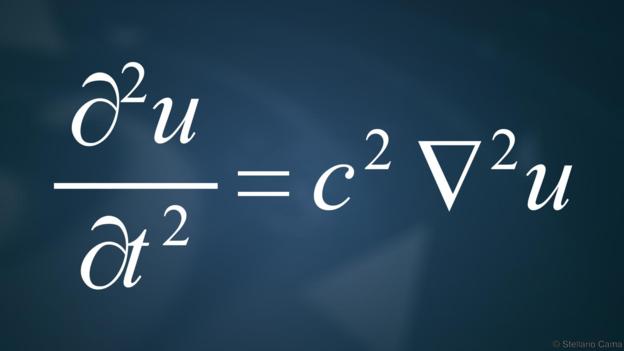
(从振动的弦到无线电波和海啸,该方程描述了波的特性)
“波动方程的美体现在几个方面,”英国华威大学的伊恩•斯图尔特说:“它具有数学的简单和优雅。它解集的区间十分有趣,并且具备优秀的数学特性。”
波动方程描述了波的传播。它适用于所有种类的波,从水波到声音和振动,甚至是光波和无线电波。
它具有非凡的历史,斯图尔特说:“它始于一个简单的振动小提琴弦的模型,并发展成用于研究各种各样的现象,从地震到石油勘探,甚至是船只的安全。它和音乐结合起来可以解释我们的耳朵听到声音,为什么有些声音组合听起来很和谐而另外一些听起来不和谐。”
“这是数学原理在某一领域拓展的典型案例,或由于自身利益在其他领域有重要的应用”,斯图尔特说:“它的美来自这些属性的组合:优雅,惊艳,深度,实用。”
(9)爱因斯坦引力场方程
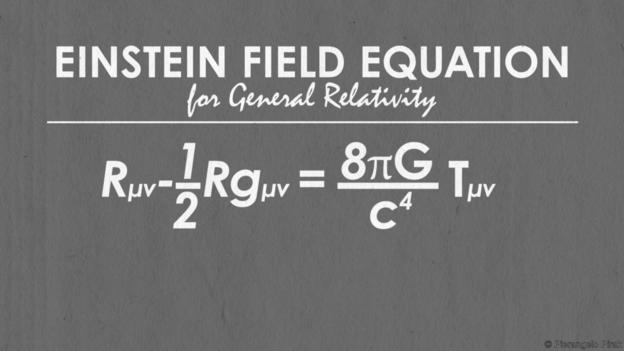
(这个方程描述了黑洞如何扭曲周围的空间,它有助于解释宇宙是如何演化的)
阿尔伯特•爱因斯坦于1915年首次提出了他的广义相对论,并在次年将其发表。它表示为一个方程,但实际上是10个方程的汇总。上面的视频解释了这一切。
该方程完全改变了我们对宇宙的本质和演化的理解,澳大利亚墨尔本大学凯蒂•麦克(Katie Mack)说: “这个新的观点是基于时空的概念,即真实世界的基本结构是可塑的。”
广义相对论提供了一种新的构想去解释引力,不是巨大的物体对其他物体施加拉力,而是扭曲了他们周围的时间和空间。
物理学家约翰•惠勒简洁地总结:“时空告诉物质如何运动;物质告诉时空如何扭曲。”
爱因斯坦的方程可以告诉我们的宇宙如何随着时间的推移而改变,并且描绘了宇宙最早期的情形。这并不奇怪,因为这正是许多科学家所喜欢的。
麦克说:“在方程所提供的视角下,我们可以获知宇宙在最基本的层面上是如何运行的。”
英国牛津大学佩德罗•费雷拉也对爱因斯坦的方程有所偏爱。
“非常认真的写在纸上,简单而又紧凑,略微有些难以辨认”, 费雷拉说,“但却是信息的宝库”。
自从爱因斯坦首次提出以来,方程一直被用于预测黑洞和引力波的存在,并推断出宇宙正在膨胀。费雷拉说:“我认为这就是为什么我认为他们美丽的,因为它们含有太多的丰富性和复杂性,因为他们看起来如此深邃又如此真实。”
(10)逻辑斯蒂映射
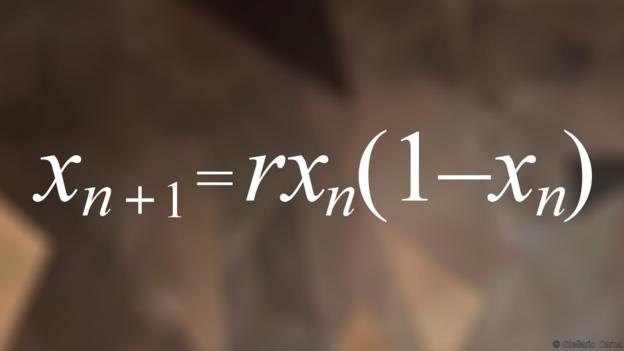
(逻辑斯蒂映射看起来简单,但它可以产生令人难以置信的复杂和混乱的结果)
逻辑斯蒂映射是混沌理论的经典例子之一。
“一句话来概括:无边的复杂源于简单的规则。” 英国伦敦城市大学的奥拉拉•卡斯特罗•奥瓦拉多(Olalla Castro Alvaredo)说到。
该方程可以用来模拟很多自然过程,例如可以模拟动物种群数量是如何随着时间的推移而增长和衰减的。
种群数量和r值的大小很敏感,如果r值介于0和1之间种群将会灭绝,如果介于1和3之间种群数量将接近一个固定值,而r值大于3.56995种群量数将会不可预测。
这些行为被数学家描述为“混沌”,他们不是我们本来期望的结果,但它们都来自于一个非常简单的数学公式。
奥瓦拉多说:“当我们惊叹于自然界的多样性和复杂性,从宇宙到微尘,我们应该铭记的是在基本层面上所有的一切都具有一些共通的简单特性。”
(11)一个“简单”的等差数列
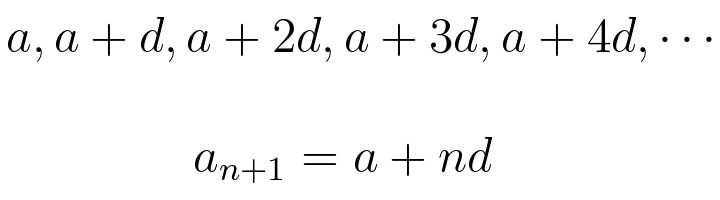
(等差数列创建了一个简单的模式,即数字永远增加一个相同常数)
等差数列是一个简单的数字序列,每次增加相同的常数。例如6, 8, 10, 12, 14, 16是一个等差数列,公差为2。很多事情我们觉得美丽是因为他们非常对称,减少我们了解他们的必要工作。英国伦敦国王学院的本杰明•多扬(Benjamin Doyon)说: “也许我们的大脑更乐于去做少量的必要工作,同时创造一种积极的美感。”
这种“算法约简”的概念渗透到所有的科学。 “我认为任何算法的约简都是美丽的。”多扬说,“当你减少必要的步骤时,你就真正的理解发生了什么。”
(12)汉密尔顿四元数方程
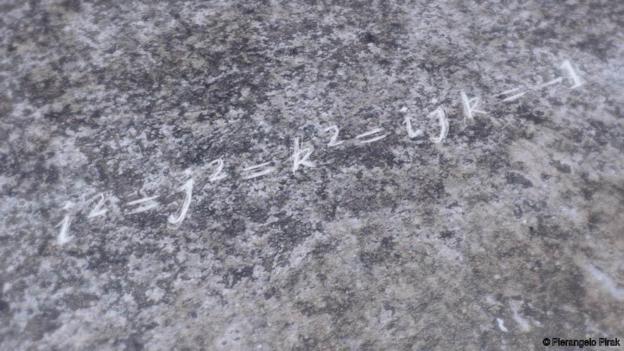
(该方程由于被爱尔兰数学家威廉•汉密尔顿刻在石桥上所被人熟知,它描述了如何计算复数,包括负数的平方根。)
威廉•汉密尔顿发现的这个方程,是一个不起眼的数学分支叫做四元数代数的核心。上面的视频阐述了它的含义。
“这个故事说的是汉密尔顿在都柏林散步的时候发现了这个方程,并炫耀地把它刻在了桥上。”英国巴斯大学的克里斯•巴德说到。
当今四元数代数是计算机图形业的核心,用于描述屏幕上对象的方向。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭