数学家发明把披萨切成异国情调形状的新方法
原文作者:雅各布·阿隆(Jacob Aron)
译文作者:333,哆嗒数学网翻译组成员,就读于中南大学数学学院。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
等你下次点外卖的时候就能用这个技能在你朋友面前炫耀了:全新而充满异国情调的切披萨方式。
大多数人切披萨都是从正中间直接切,但是要是披萨当中部分有一个食材配料呢?这是很多人宁愿避免切到的,不过这时一旁的人可能已经迫不及待地想用脆皮蘸酱开吃了。
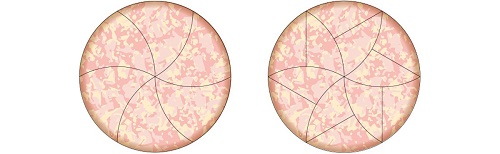
数学家之前已经想出了一种切披萨的方式——正式说法是“单面圆盘平铺”(monohedral disc tiling)——这种方法能够让你切出12块完全一样的披萨,其中的六块组成一个从中心延伸出的星形图案,另外的六块分割了边上剩下的脆皮部分。具体要怎么做呢?首先你要切三道穿过披萨中心的弧线,然后把切出的小块每个一分为二,如下图所示。
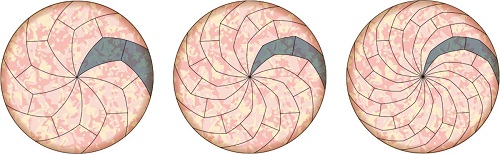
现在,英国利物浦大学的乔尔·哈德利和斯蒂芬·沃斯利推广了这个技术,创造了更多的切法。这两个人证明了利用任意有着奇数条边的“曲边披萨块”,如5边、7边等(即下面的阴影部分),能够创造出相似的的平铺方式,接着只要像之前那样把它们等分为二就可以了。“从数学上来说,这种操作可以无限进行下去。”哈德利说道,尽管你可能会发现对于超过9条边的披萨块,再要实施上述步骤已经不切实际了。
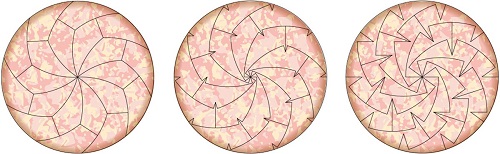
哈德利和沃斯利甚至更进一步,通过在边角上切出楔形,创造出怪异的、带尖角的披萨块,这些披萨块仍然组成一个圆(下面这张图展示了5边披萨块的这种情形)。哈德利说:“这真是令人惊奇。”
正如许多数学结果一样,它的用处并不会立刻显现。另外一个披萨定理也是如此,它表明了当一个披萨被随意的、不经过中心的切割后会发生什么变化。
“我不知道我们的成果除了用来切披萨外还会有什么用处。”哈德利说,他已经实际尝试过用这种方法去切披萨(如下图)。但这个结果“在数学上很有趣,并且你能由此制作一些漂亮的照片。”

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭