数学告诉你结婚吧,别再约了!
原文作者,Ana Swanson,Wonblog记者,原文发表于华盛顿邮报的网站上。
译文作者:小王子,哆嗒数学网翻译组成员。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
出于各种各样的原因,人们怯于对伴侣许下承诺。原因之一就是,他们无法预料未来会不会有更好的在等着他。早早地确定关系,意味着你放弃了将来会遇见更完美恋人的可能。倘若拖着不表态,那么所有美好的都将错失。人们即便不想与初恋结婚也不想拖得太久。
这个选择对于有完美主义倾向的人而言更是两难。事实上已经有一个简单的数学规律可以指导你走出困境,它能计算出你要寻找多久的伴侣才会决定安定下来。
这个数学问题有很多为人们所熟知的名字——“秘书问题”,“挑剔的求婚者问题”,“苏丹的嫁妆问题”,“见好就收问题(止步问题)”。问题的答案虽然已经由几个数学家得出了,可是直到1960年,在数学爱好者Martin Gardner将答案发表在《科学美国人》后才被普及。
这是一个你需要从一定数量的选项中做出选择的场景。假设你一生中会遇见11个可以认真约会并且决定安定下来的潜在伴侣。碰巧地,你在同一个时间遇见了他们,那么你将毫无疑虑地选出你的最佳伴侣。遗憾的是这样选择终身伴侣的方式明显是不现实的。
其中之一的问题就是追求者出现的顺序是随机的,而你又无法判断现在的追求者与将来会遇见的追求者相比谁更好。现在的同伴是否只是过客?还是说他或她已经是你的真爱了?还有一个问题是,一般情况下,被你拒绝过的追求者与你之间的关系很难再回到过去了。

那么,到底该如何寻找你的另一半呢?可以说,这就是一种赌博。并且和大多数的赌博游戏一样,它有一个非常吸引人的头奖,而且你可以知道并提高自己获得头奖——最佳伴侣的机会。确实存在这样一个可以增加你的胜算的奇妙答案。
这个奇妙的数字是百分之三十七。要想以最高的机会挑选到最佳求婚者,你应该考虑并拒绝你一生中前37%的追求者。(如果你对数学感兴趣,你就会知道0.368或者说36.8%来源于1/ e。)事实上,你只要遵循一个简单的规则:如果遇到了比任何一位前任都优秀的,那就选择他。
要想将这个规则运用到现实生活中,你必须得知道你一生中会有多少位可能拥有或希望拥有的追求者——而这是不可能明确知道的;你还必须判断出谁有资格作为备胎,谁又只是一时冲动。而这些问题的答案都不是清晰的,所以你只能去估计。在这里,我们假设你在你的人生历程中将有11位真诚的求婚者。
如果在11个追求者中随机选择,你选出最佳伴侣的概率约为9%。但如果你使用了上述的方法,挑选出最佳伴侣的概率将明显增加到37%。这虽然不是一个肯定的概率,但远胜于随机选择。
数学家汉娜·弗里曾在2014年TED上迷人的谈话中揭露过,这个策略不能保证百分百成功的,而是有风险的。比如说,你所遇见的是下面的插图中描绘的情景,你的初恋就是你最完美的另一半,按照规则,你无论如何都会拒绝他。而当你继续和其他人约会时,再没有能比你的初恋更好的人出现了,可以预料到,你会拒绝所有的追求者,决定和你的猫相依为命。(当然,也不排除有人会更喜欢让猫来当男朋友或女朋友的可能性)。
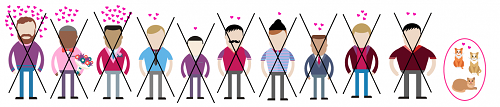
下一幅插图表现的情景或许会更现实一些:当你在你的情感世界里先遇见的是一连串不靠谱的前任。按照规则,即使你下一位约会的对象只比你的前任们好那么一点点,你也还是会嫁给他。但是他任然不是一个好的对象,而实际上未来还有更好的。

有很多方法可以证明这个策略是会出错的。但与任何其他的方案相比,不论你想考虑的对象是10位追求者还是100位追求者,它依然是你最值得期待的指导你获得真爱的方法。
这个策略是如何起到作用的呢?一旦你决定在茫茫人海中认真地寻找一位候选人的时候,它的作用就会突显出来。你既想和足够多的人约会以掌握选择权,又不想选择太久而增加错过理想情人的风险。于是,你就需要借助这样一个可以权衡是太早还是太迟安定下来的风险的准则。
这个逻辑在越小的例子里可以越清晰地解释清楚。不妨设在你的一生中你只有一位求婚者。如果你选择了那个人,那么你就永远地赢得了这场赌注,他或她就是你一生的陪伴。
如果你有两个追求者,那么现在就是有一个平分秋色的机会可以挑选到最好的追求者。这种情况下,你是用我们的策略——在选择一位候选人前考虑过另一位候选人还是用其他的方法都不重要。因为无论你用什么方法,你选到真爱的概率都是50%。
但是当追求者变多的时候,你就将注意到秘诀到底是如何帮你获得真爱的。下面的图比较了从三位追求者中随机选择到真爱的成功率。每位求婚者被置于自己的方框中,并根据他们的品质排了序(一表示是最优,三表示是最差)。如果你按照策略中指导的那样做选择,你会发现,在一群追求者中获得真爱的机会显著地增加:
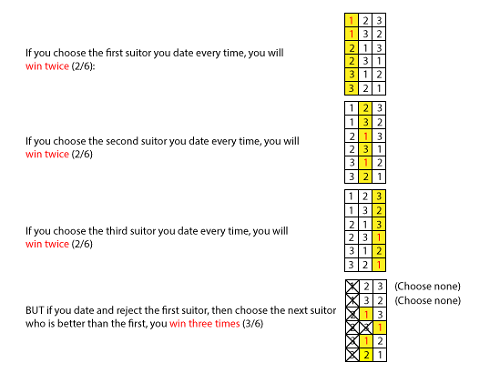
图中:如果不论什么情况都选第一位追求者,你选到真爱的次数是2次(2/6);
如果不论什么情况都选第二位追求者,你选到真爱的次数是2次(2/6);
如果不论什么情况都选第三位追求者,你选到真爱的次数是2次(2/6);
但是如果你考虑并拒绝了第一位追求者,在之后的追求者中选择比之前好的那位,你选到真爱的次数是3次(3/6)
数学家们在不断重复上述过程时发现一个有趣的规律:当“追求者”趋向无穷大时,在求得真爱之前,你需要考虑和拒绝的追求者的最佳数量是收敛于一个特殊的数字——37%的。
在数学领域中解释这个策略是如何起到作用的,又是另一个通俗易懂的数学知识,这与神奇的自然常数e有关。e是唯一一个可以在统计学中描述在只有成功和失败两个结果的统计试验中成功的机率的数字。(可以在二项分布中起独有作用的数字?)
长话短说,凭这个策略,不论你所评估的对象是追求者,还是其他重要的东西,公寓,房子,或是卫生间,你在未知序列中都有最大可能选到最合适的对象。
其他变形问题
还有一些问题的变形,根据不同的变动,结果也将稍作变化。
在上述的场景中,你的理想就是是最大限度地提高你在一群追求者中找到真爱的机会——如果你找到了真爱,你就是赢家;如果你选择的是其他任何一个人那你就是失败者。但在现实中,更多的是像数学家Matt Parker笔下的那样的情形,“如果得到的比最好的不差多少,这只会给你带来微不足道的不悦。”你并不一定要求最好的,即使选择了次好或第三好的,你也依然很满足,那么孤独终身对你而言依然遥远。
如果你的理想就是找一个很好的相伴者,而不是最好的那一位,那么这个策略也要随之改变了。在这种情况下,不妨设你一生中会遇见n个求婚者,那么,在决定接受任何人之前,你将考虑并拒绝的求婚者是根号n个。正如上面的公式,过了这个准点,错过理想伴侣的赔率就将超过早早就获得真爱的赔率。就像在上述11个追求者的模型中,30%就是那个错过理想伴侣的风险超过早早获得真爱的准点。因此,你只需考虑并拒绝一生中前30%的追求者,而不必再遵循之前的数据37%了。
总而言之,这个方法意味着你会更早地选好伴侣安定下来。并且你有很高的机率和非常好的人相伴终身,同时还降低了孤独终身的概率。根据帕克说法,在10个人之间做选择,使用这个方法你将获得的基本上是你有75%概率满意的人。在100个人的选择中,你将选到的基本上就是你有90%概率满意的人了,这已经比大多数人希望的要好多了。
1984,一位名叫Minoru Sakaguchi的日本数学家进一步升级了对这个问题的处理,因为她发现坚强独立的男性和女性会更有魅力。在sakaguchi的模型中,有这样一些人,他们虽然想找到他们的真爱,但他们更愿意过独身生活。在这种情况下,人们直到考虑了约60.7%的候选人才会寻找可以确定关系的人。你注意到,一旦人们不再在意自己是否会孤独终老,他们将很乐意考察更多的候选人,收集更多有关他们的信息,自然而然地也会有更大的机会选择最最棒的那位。
虽然说这些模型都是理论上的,但它们也支持了一些交往方面的传统观点。首先,想要选择一个人安定下来他给我们无法拒绝的理由去认真交往。如果没有约会的经历,你就没有足够的认知在约会这潭深水中理性地做出选择。最普遍的情况就是你会认为你遇见的第一或第二段情感就是你的真爱,当然也不排除例外。
其次,你什么时候安定下来和你的要求也是有关的。如果你想找一个非常好的对象来减少你最终孤独的机会,经过审查和拒绝在你一生中可能拥有的前30%的追求者之后,你就该早早地安定下来了。
但如果你确定自己的目标就是从追求者中找到最好的,那你不妨等待久一些,审查和拒绝了追求者总数的37%后再确定关系。如果你想找到你的完美配偶,并且你也不介意孤独终身,那你可以再耐心些,在考虑和拒绝60.7%的追求者后再开始寻找你的伴侣来结束单身,这些方程既让那些担心会错失真爱的人安心,也指导了那些因为不知道他们将来会失去什么而怯于对同伴许下承诺的人。这道数学题恰巧指导了你不必为了不错过真爱而大海捞针。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭