数学告诉你勒布朗•詹姆斯从来没手热过
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
作者,南梦玲,绳索技术协会理事。
数学在生活中不可或缺,这也许是老生常谈了。数学嘛,买菜总是要用到的,加价减减而已。也许很多文章介绍过数学的伟大用处,但实际上也过于脱离生活了,数学用于制造电子设备?管他呢,我自己能用就好了。数学能用于金融?对于玩不起钱的我来说,还是算下工资多少年能买房更切实际。能发射火箭去上天?上去的又不是我。你们别整这些高大上的东西,数学对于常人还真是加加减减仅此而已了。
果真如此吗?
我们先来看一个例子,请看下面这两位想要降低其成本的车主。
小明(小明终于长大了)原来的车每升汽油能跑12公里,现在他换了一辆更省油的车,每升能跑14公里。
小丽爱护环境,她把原来每升汽油跑30公里(好节约的耗油!)的车换成了每升汽油跑40公里的车。

假设这两个车主一年的行程是相同的。换了车之后,谁省油的数量更多?这问题太简单了吧,加加减减而已,小明每升提高了2公里,等于是提高了六分之一,而小丽每升多跑了10公里,提高了三分之一!肯定是小丽更加省油!这是一个小学知识就能解决的问题,大部分人直觉口算都是这么认为的。好,现在我们再来算下,假设两人都跑了10000公里,小明就从833升减少到了714升,共省了119升,而小丽从333升降到了250升,只省了83升油,实际上小明更省油!
好吧,小编我并不是想要来证明大家小学没毕业,而是想要告诉大家,做广告的最高境界就是,明明说的都是实话,却依然让观众的直觉产生偏见,从而去购买产品。我们每天都会看到各种信息,并且会对这些信息有一个主观的理解,其实我们的主观理解未必有多正确,生活中充满了偏见。这个问题之所以产生直觉错误,是因为描述的人采用了每升汽油行驶的公里数的框架。为了防止此类问题的出现,我们应该采用每公里耗油多少升的框架来描述。错误直觉很容易误导政策制定者和买车的人。以上描述的现象,心理学家查德•拉里克(Richard Larrick)和杰克•索尔(Jack Soll)研究过,他们2008年在《科学》杂志中发表了的《每加仑汽油所跑英里数的错觉》中有详细讲解。
我们再来看一个例子,2014年一项研究对中国2856个县的肾癌发病率进行了调查,调查显示2014年该病发病率最低的县差不多位于西部和西部人口稀少的乡村,对此你有何看法?
人们很容易就做出推断,认为肾癌发病率低主要是由于乡村的生活方式很健康——“没有空气污染和水污染,食品没有添加剂,保证新鲜。”这一点完全说得通。我们依赖直觉得出这一结论,并且看似很有道理,但实际上果真如此吗?如果把描述改为发病率最高的县位于西部和西部人口稀少的乡村,相信人们可以毫不费力的做出推断:“乡村生活贫困,人们无知、医疗条件差、不注重卫生、嗜烟等。”虽然这两个理由都看似很有道理,但一个地方不可能在同一时间发病率又高又低。
之所以会出现这种情况的原因,是因为我们的直觉存在偏见。问题的关键在于乡村地区人口稀少,仅此而已。稍微学过概率的人,都可以很快的反应过来:“样本数量越少,极端事件连续发生的概率就越大。”举个例子,我们仍1个 骰子,连续扔3次全是6的概率远远大于连续扔30次全是6的概率。在没有大数定律支持的情况下,一切仅仅是运气罢了。不信的话你可以尝试去计算这个题目:在一个装有两种颜色的箱子中有超多的红球和黑球,其中红球黑球一样多(这相当于在说,癌症比例为50%),小明每次拿4个球而小丽每次拿7个球,那么分别去计算两个人拿出来的全是同一种颜色的球的概率(发病率100%或发病率0%),可以发现小明的概率大概是小丽的8倍(12.5%与1.56%)。这就是真相,某县人数少,因此更容易出现极端事件,而恰好赶上了数据调查,人们就容易得出错误的结论。统计学家霍华德•维纳(Howard Wainer)曾经做过一个实验,来解释类似的现象。

“现在勒布朗连投几个都进了,手热的发烫!队友应该尽量把球都传给他多打!”这是我们看篮球的时候,经常听到解说说的话,也是我们要说的第三个例子。篮球运动员有时候会有投篮手风很顺的现象,如果一个运动员连续进了三四个球,那么人们就会不由自主做出判断:这个球员现在正处于手热状态,得分率暂时增加。两队队员都持这种判断——队员也更爱将球传给打得手热的人,对方球队则会加强对这个球员的防守。然而真实情况是,通过统计学研究表明,根本没有投篮手热这一回事,之所以会有这样的错觉,是因为人们太快做出了评判。再更多次观察之后你就会发现,球员的得分率将会回归他的正常水平,也就是回归平均值。统计学告诉了人们事实,却没多少人相信这个事实。做这项研究的是阿莫斯•特沃斯基(Amos Tversky)、汤姆•季洛维奇(Tom Gilovich)和罗伯特•瓦隆(Robert Vallone)。

我们的思维经常会对事物产生偏见,直觉也会欺骗我们,而人们往往却不肯承认自己思想的错误。这些事例里边蕴含着最基本的数学原理,并没有什么高大上的理论,不需要微积分,也不用研究群环域,只要简单应用高中以下的数学知识,就可以避免我们做出错误的判断。
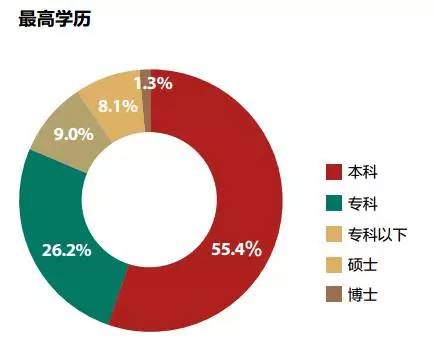
接下来我们再看第四个例子,如果你在北京地铁上看到一个人正在读知识专业性比较强的报纸,那么他学历更有可能是博士还是根本没读过大学?我们的直觉会告诉我们,应该选第一项,但实际上这样选择并不明智。因为在地铁上面是博士的人的基础比例远小于没有本科文凭的人的基础比例(1.3%和35%)。
这里我们来看一个贝叶斯定理应用的经典例题:
一辆出租车肇事逃逸,这座城市有两家出租车公司,其中一家公司的车全是绿色的,另一家全是蓝色的。
你知道这座城市85%的出租车是绿色的,15%是蓝色的。
一位目击证人辨认出那辆肇事出租车是蓝色的。当晚,警察在出事地点对证人的证词进行了测试,得出结论是:目击者在当时能够正确辨别出这两种颜色的概率是80%,错误的概率是20%。
这场事故的出租车是蓝色而不是绿色的概率是多少?根据贝叶斯定理,目击证人得出正确答案的概率为41%。
当人们面对这样的问题的时候,往往会忽略基础比率,只考虑目击者因素,因此大部分人会认为是80%。
在这里,我们需要用贝叶斯定理来约束我们的直觉,才更有可能得到正确的答案。生活中我们的直觉往往忽略事件的基础比率,所以我们会产生偏见与错误。
现在,你还敢说数学仅仅是加加减减,和生活无关吗?这四个事例,都是我们生活中常见的事情,但我们很容易就被我们的直觉所欺骗,对其产生偏见。数学可以给我们的生活我们的判断带来指导性建议,直觉往往欺骗自我,善用数学思维,而不是仅仅依赖直觉,能够让我们减少偏见。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭