一个关于开普勒方程的的实用解法

原文作者：Marc A. Murison，美国海军天文台，华盛顿特区。

译文作者：

radium，哆嗒数学网翻译组成员,就读数学专业

donkeycn，哆嗒数学网翻译组成员,华东师范大学数学博士

校对：小米

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

摘要

我们呈现了一个开普勒方程的数值解法。这个方法实用又快捷，同时对CPU的运行时间进行了优化。

关键词：天体力学二体问题开普勒方程

1、引言

开普勒方程联系了线性流逝的时间与非线性的两个天体m1和m2相对于它们的质心做开普勒运动时的相对角位置。即：

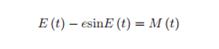(1)

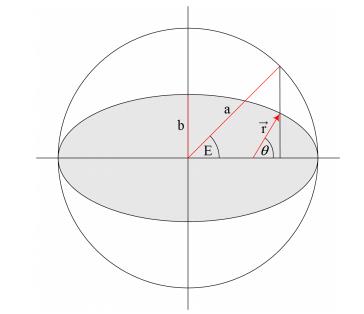
其中E是偏近点角，e是轨道离心率（或轨道偏心率），M (t) = n (t − τ )是平近点角，n是该二体运动的平均角速度，τ是行星经过近日点(注：此时可认为是行星绕恒星运动，近日点即行星与恒星距离最短处)的时刻，a是椭圆轨道的半长轴，a与n满足n²=G(m1+m2)/a³。参见下图。

我们将在这里概述如何推导一个开普勒方程的数值解法。理想情况下，一个方法是否实用，应该看它是否同时具备以下两种特质：（1）计算E的CPU时间是否最小化（2）程序的复杂度是否最小化。这两个需求往往是互相制约的，但幸运的是我们可以找到一个折中的方法来解决这个矛盾。一个更详细和完整的方法会在另一篇文章中讨论，这里我们主要强调实用性。

开普勒方程是超越方程，故它的解只能通过迭代法得到。因此，任何一个数值设计的过程都有两个任务。第一个任务是设计迭代循环中的逼近算法；这个逼近算法需要重复直到结果达到令人满意的精度。一般说来迭代公式所用的阶数越高，迭代所需的次数就越少。然而，更高阶的迭代公式将使得公式的表达式变得十分复杂，这将极大地耗费CPU的运行时间。因此，无论我们选择何种算法，一个适当（通常是比较低）的阶数会使得CPU的时间耗费最短。第二个任务是选择一个迭代循环的初始值，初始值选的越精确，循环将收敛的越快。选择初始值的方法不需要和迭代方法一样，哪怕极其相近。类似于迭代算法，对于一个给定的确定初值的算法，将有一个理想的阶数能够最大限度地减少CPU的时间耗费。

接下来我们将给出一个特别简单的确定初值的方法，在那之后会给出一个快速迭代法。而第五部分，我们列举的其他研究成果表明，这里总结出的对于每种方法的阶数的选法都是理想的。紧接着是一个使用这些方法的快速和傻瓜式的程序。幸运的是，你将吃惊地发现它十分简单，而且很容易移植到各种数值计算语言。

2、初值法

由于我们必须用迭代法求解开普勒方程，我们给循环迭代的初始值越精确，效果就越理想，至少在迭代表达式的复杂性变得令人反感之前应该是如此。我们有开普勒方程

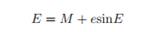（2）

在离心率为0的这个极限情况下，我们有E = M；这是最简单的初始值近似。因此方程（2）暗示了如下改进此近似的简单迭代公式：

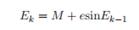（3）

其中初始条件E0 = M。我们可以对迭代递归表达式（3）进行反复迭代，直到得到我们希望达到的E的任意高的阶数。例如三阶近似公式：

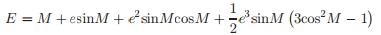（4）

公式（4）对应的计算时间最优化的三阶伪代码如下：

KeplerStart3 := proc(e,M)
local t33, t35, t34;
t34 := eˆ2;
t35 := e*t34;
t33 := cos(M);
return M+(-1/2*t35+e+(t34+3/2*t33*t35)*t33)*sin(M);
end proc;

3、迭代法

因为（1）是超越方程，无论是数值求解还是解析求解，我们都必须使用迭代法。所以当给定一个具有一定误差E的时候，我们必须找到一个迭代公式，使其返回一个误差更小的近似值。同时它也必须是收敛的。基于这种情况，我们按如下方式改写方程（1）：

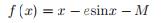（5）

式(5)中，f(x)= 0的解是x = E 。设ε=x-E是用x近似E时所引起的误差。将f(x)在x = E处进行泰勒展开，我们得到

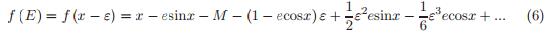（假设 ε 充分小）

只考虑式(6)到ε的1阶项，求解可得

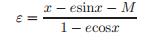（7）

我们可以把这个作为一阶迭代公式的核心部分。假设我们一开始的猜测是x = x_0，那么x_1 = x_0 + ε比x0更接近于E。我们得到如下一阶迭代程序：

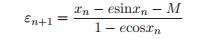（8）

其中初始值x0的取值将在后面讨论。由(8) 我们可以得到一个单步一阶迭代方法来估计E_{n_1}=E_n – ε_n 。式(8)对应的伪代码程序是

eps1 := proc(e,M,x)
return (x-e*sin(x)-M)/(1-e*cos(x));
end proc;

现在把ε的二阶项考虑进去，方程（6）的霍纳形式是

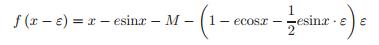（9）

在方程（9）中令f (x − ε) = 0，整理得到如下形式：

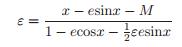（10）

我们可以通过分析方程（8）来创建一个二阶迭代形式：

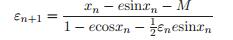（11）

我们还可以创建一个两步迭代过程，具体过程如下：首先计算方程（8）给出的ε_n ，然后计算方程（11）给出的ε_{n-1}。我们也可以直接跳过中间步骤，直接把方程(7)给出的ε_n代入方程（11），得到单步迭代为

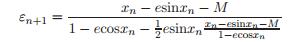（12）

关于方程（12）的一个优化后的伪代码为

eps2 := proc(e,M,x)
local t1, t2, t3;
t1 := -1+e*cos(x);
t2 := e*sin(x);
t3 := -x+t2+M;
return t3/(1/2*t3*t2/t1+t1);
end proc;

关于函数f(E) = f(x − ε)的三阶近似的霍纳形式为

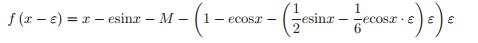（13）

令方程(13)为0，解出“最外层”ε，放在右边，我们有方程：

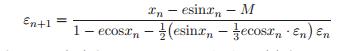（14）

（在方程（14）中我们或许可以用方程（12）代替ε_n使其变为二步迭代方法，或在方程（11）中用方程（8）代替ε_n变为三步迭代方法。又或者，我们可以在（14）中直接用（12）代替ε_n，从而得到一个单步三阶方法，后者优化后的伪代码为

eps3 := proc(e,M,x)
local t1, t2, t3, t4, t5, t6;
t1 := cos(x);
t2 := -1+e*t1;
t3 := sin(x);
t4 := e*t3;
t5 := -x+t4+M;
t6 := t5/(1/2*t5*t4/t2+t2);
return t5/((1/2*t3 - 1/6*t1*t6)*e*t6+t2);
end proc;

我们可以继续利用这种方式到更高阶的形式。

4、真近点角与偏近点角之间的互相推导

如果有人需要使用真近点角θ 而不是偏近点角E，我们可以参考前面的图对它们进行转换。由图可知，位置向量的大小可以写为：

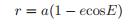（15）

观察图1，我们有

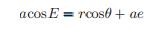（16）

从方程（16）我们可以推导出

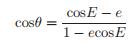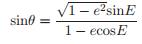和（17）

从方程（17）用θ反解出E，我们得到

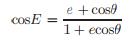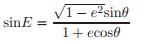和（18）

因此，在必要的情况下，我们可以使用迭代程序去求解我们开普勒方程中的E，然后使用方程（17）解出θ。

5、总结：一个有用的数值方法

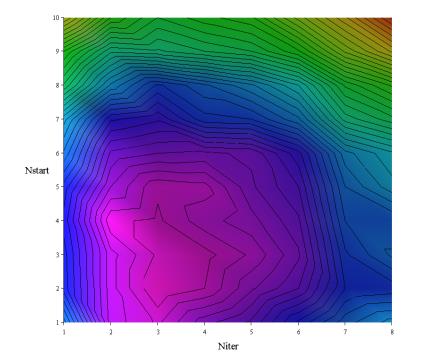
（作为初始值精度 (Nstart)和迭代阶数(Niter)的二元函数，等高线表示在每一个(Niter, Nstart) 点上求解160000个开普勒方程花费的CPU总时间。这160000个方程的e和M从{ R×R:e∈(0,1),M∈(0,π)}的一个等间隔400×400网格域中选取。从上图看，每个方法的三阶算法都接近最优）