数学家是怎么玩连线游戏的?
原文作者:Kevin Knudson,佛罗里达大学数学系教授。
译文作者:Y. W.,哆嗒数学网翻译组成员,就读于北京四中。
校对:donkeycn
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
我们都玩过连线游戏。一张图上有一组标好号的点,我们从数字1开始一个个连线段,一直连到最后就能看到一个图案。

上面这个连线游戏的图案是太阳。
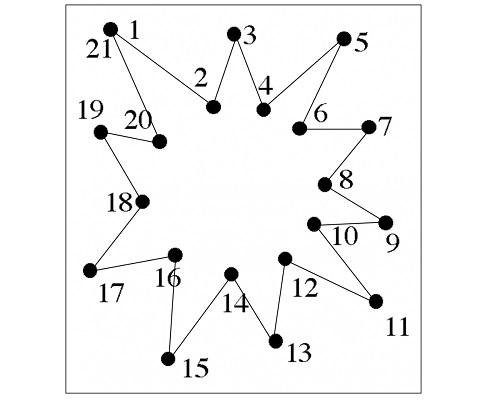
这简单的连一个小孩儿都能做,更别说一个数学家了。
因为我们的点是有顺序的,而且我们知道要按顺序连点,所以我们可以玩这个游戏。但是,在实际生活中,我们经常遇到没有标号的点。那怎么连点才能连出一个有意义的图片呢?
我们可能不想把离的太远的点连到一起,比如我们不太可能想到把上图中在整张纸的两侧的1和13连到一起。那么到这里就需要一个标准了,到底怎样算远?怎样算近?这里可以参考沃罗诺伊图。
给定平面上的一些点,平面被划分为相应的区域(每个平面上给定的点对应于一个区域),使得每个区域中任意一点距对应的给定点比距其它任何给定的点都近,每一个区域被称为一个沃罗诺伊胞腔,这样就得到了沃罗诺伊图。下面是一个例子(一张平面上有八个点的沃罗诺伊图):

画一张沃罗诺伊图并不难:首先作出任意两点的垂直平分线, 这些垂直平分线形成了沃罗诺伊胞腔的边界。举个例子,在上面的分割中,中间的红色胞腔包含了距离中央的给定点距离比距离其他给定点近的点。虽然这个红色胞腔是一个有界的区域,但是其他的胞腔可以是无界的(比如右上角紫色的胞腔 )
当我们完成了这一步,就可以开始德劳内三角剖分了。德劳内三角剖分就是按照一个特定的规则连点。形式上,德劳内三角剖分是沃罗诺伊图的对偶图。但是如果你不知道上面这句话的意思,也没关系,因为这个过程很容易描述,只要对应点的沃罗诺伊单元胞腔有一公共边,我们就把它们用一条边连接起来。这保证了我们只连接“近”的点,而非 分别位于给定点集两侧的2个点。
那么,我们刚刚连出太阳的图会变成什么样子呢?来看看下面的沃罗诺伊图(给定点集的沃罗诺伊胞腔)。
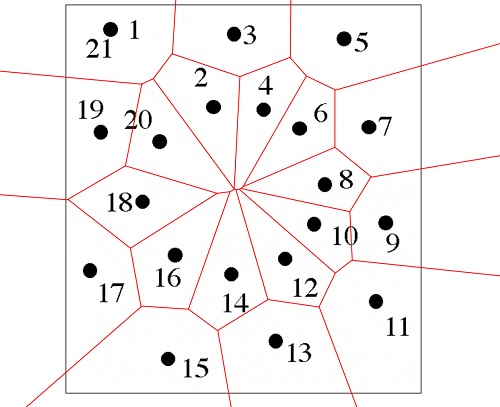
好像和数字没有什么关系……不过没关系,现在来看看在沃罗诺伊图上建立的德劳内三角剖分(黑线为德劳内边)
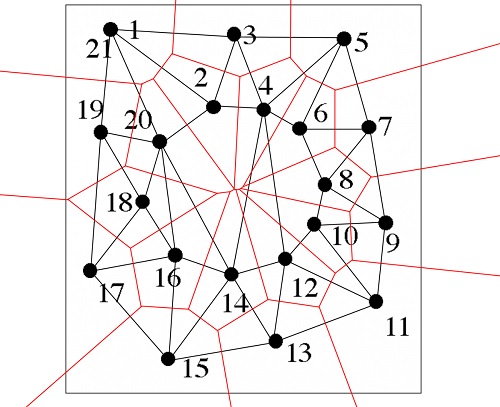
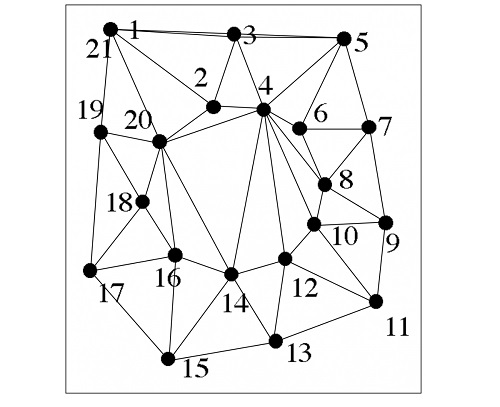
现在我们可以看到一个暗藏的太阳了。但是,我们不仅连上了相邻的点,还意外连上了几个在圈 上的点。总的来说还是不错的,而且这个方法也很简单。 虽然这样,还是有一些问题的。这个方法可以在更高维的空间中运用,但计算会变得繁琐。 给定d维空间中的n个点,对应的沃罗诺伊图具有n^(d/2)(n的d/2次方) 个点。也就是说,如果d比2大很多的时候,要得到相应的沃罗诺伊图,将会不胜其烦。
沃罗诺伊图有一段广为流传的历史,包括在解决1854年伦敦霍乱爆发事件中著名的应用。医师约翰•斯诺通过不同的井分割城市,从而排查致病的水源。德劳内三角剖分还应用在在国土建模和其他曲面的可视化中。随着新计算技术的到来, 寻找能更好应用德劳内三角剖分(“应用德劳内三角剖分”改为“得到沃罗诺伊图”)的算法已经变得非常重要。
麦克•波斯多克使用机场的位置作为给定点划分的美国地图,我个人最喜欢的沃罗诺伊图。
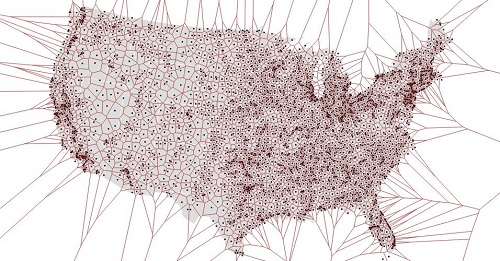
詹森•戴维斯制作了一张世界机场沃罗诺伊图。这张沃罗诺伊图可以让你旋转地球表面。(传送门:https://www.jasondavies.com/maps/voronoi/airports/)建议你看看这个,挺好玩的。
现在你知道数学家是怎么连线的了,这可不仅仅是一个小孩玩的游戏哦。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭