烧脑:乒乓球、无穷与幻术超能力
原文作者:Ken Wessen,理论物理与人类生物学博士。
译文作者:333,哆嗒数学网翻译组成员,就读于中南大学数学专业。
校对:小米
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
在这篇文章中,我打算用三个幻术让你惊奇不已。它们真的非常美妙。在这三个幻术中,正是无穷的概念让你的大脑一团乱麻。我想在意识到它是一个多么疯狂、令人激动的概念这一过程中,你会享受很多乐趣。
首先,我想让你思考一下由无穷多个物体组成的一个整体,或者说无穷集合,它的大小是什么。一个集合的大小简单来说就是它所包含的元素的个数。两个集合被认为是一样大的,如果至少存在一种方式能够将一个集合中的每个元素精确对应到另一个集合中的一个元素,并且每个集合里面都没有元素没被对应。

这个定义是有它的道理的。集合{1,2,3}与集合{A,B,C}是同样大的,因为我们可以这样作一个对应:1 ↔A,2 ↔B,和3 ↔C(当然,还有别的方式让它们一一对应起来,不过我们只需找到一个就行。)然而,当我们处理无穷集合的时候,事情就变得更有趣了。举个例子,考虑由所有正整数组成的集合{1,2,3,4,……}它和所有偶数组成的集合{2,4,6,8,……}是一样大的!这听起来很疯狂,扔掉第一个集合的奇数部分却仍然给我们留下了一个大小没变的集合,因为我们可以让它们的元素这样对应:1↔2,2↔4,3↔6,……第一个集合中的任意一个元素在第二个集合中都有唯一的元素与之对应,也就是它与它自身的两倍一一对应;同样,第二个集合中任一元素都可以和自身的一半建立对应。没有元素被漏掉,也没没被对应到的数;所以,奇怪的事情发生了,两个集合是一样大的。其它和正整数集大小相同的集合还有奇数集、由10的倍数组成的集合,甚至是由所有分数组成的集合。(这样的集合我们称之为可数无穷。)
现在我即将描述一个思想实验,用来展示基于这一事实的一些出人意料的结果。
打包乒乓球
让我介绍一下克拉克。他有一项超能力,能够让他完成一个数学家们口中的超级任务——在有限的时间内完成无限多的步骤。在这里,我们限定时间为一个小时,11:00开始,12:00结束。
有无穷多个乒乓球可供克拉克使用,并从1开始标号;还有一个袋子,克拉克可以用它来装乒乓球。
在11:00时,他拿起了第一批10个球,标号1,2,3,…10,并把它们放进了袋子里。接着,他从袋子里拿出了标号为10的球,其他的九个被留下。到现在为止,这些都小菜一碟,还没用到什么超能力。这时克拉克也应该休息一会,喝杯茶,因为接下来事情就不容易了。
等了30分钟,11:30,克拉克把标号11,12, …20的球放进了袋子里,又从中取走了标号为20的球。
又等了15分钟(11:45)他把标号21到30的球放进了袋子里,并取走了标号为30的球。
克拉克一直这么操作,总是先放进去10个球,又拿走第十个,但是每次等待的时间都变成了前一次的一半。
显然克拉克将要这样操作无数次才能把无穷多的乒乓球放进袋子里。所以,他能完成任务吗?
答案是肯定的。如果我们把克拉克在将下一批球放入袋子之前所等待的时间间隔加起来,就得到了和式(以小时为单位的分数形式):
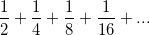
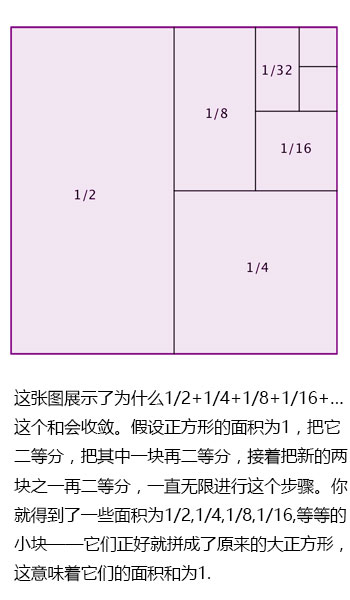
12:00时,当这个过程完成了,克拉克的袋子里装了多少球呢?
每一步,克拉克放入了9个球,这样操作了无穷多步,所以袋子里将会有无穷多个球。事实上,在所有正整数中,只有那些标号为10的倍数的球不在袋子里。这些真的都很显然。还没出现令人感到迷惑的事情——只需要集中一点点精神去仔细想一下这个无穷的过程。
但是,下面的事情就开始令人困惑了。

第一个幻术
假设,当克拉克在做这个实验的时候,他的朋友布鲁斯也在把无穷多的乒乓球放进一个袋子里。但是,他稍稍用了点不同的策略。
在11:00,布鲁斯拿起了第一批10个球,标号1, 2, 3, … 10,把它们放进了袋子里,但是他把标号为1的球从袋子里取走了。接着,在11:30,他把下一批10个球放了进去,标号为11, 12, … 20,又从袋子里取走了标号为2的球。15分钟后,在11:45,他把21到30号球放进了袋子,又从中取出了标号为3的球。一直这么操作,每一步放入10个球,但是又从袋子中取出标号最小的那个球。
布鲁斯的方法和克拉克的在本质上是否一样呢?嗯,每次他放进去10个球又取走1个,所以,看上去当然是一样的。
在12:00,当克拉克和布鲁斯比较他们各自袋子中乒乓球的个数时,他们会看到什么情景?
我们知道克拉克的袋子里含有无穷多个乒乓球,但是,令人难以置信的是,布鲁斯的袋子里一个球都没有!是的——0个。每个球都会被取出袋子。
思考一下:什么号码的球能留在袋中呢?这些球被标号为1,2,3…直到无穷,但是每个数字都一一对应这无穷多次放入-取出步骤中的一个,所以每个球都会被取出。举个例子,20号球在第20步时被取出,1529号球在第1529步时被取出,1327821号球在第1327821步时被取出。它们都消失了!
哇哦!太疯狂了。克拉克有无穷多个乒乓球,布鲁斯却一无所有。(作为一个有趣的转折,假想一下,这个实验不是用的乒乓球,而是用英镑的硬币,你被允许保留到了12:00时袋子里剩下的所有硬币。)
但是,当你想知道如果他们在时间结束前检查会发生些什么时,这甚至更为荒诞。
第二个幻术
假设布鲁斯和克拉克每一步都检查一下袋子而不是只在12:00检查那一次。他们会看到什么情景?
在12:00之前的每一次检查,他们都将会看到有相同数量的乒乓球。这是真的——每一次他们检查,乒乓球的数目都将严格相等。只有在精确的12:00那一刻,当无穷多的操作步骤被完成,才会出现差异——多么巨大的差异!那看起来就像是布鲁斯所有的球都在一瞬间消失无踪。
第三个幻术
理解并计算克拉克与布鲁斯的结果依赖于球的标号,所以现在让我们设想第三个超级英雄,戴安娜,也在那里做着相同的事情——每步放进去10个球,取出1个球。但是,戴安娜的乒乓球没有被标号并且是完完全全的不可区分。
在12:00时,戴安娜的袋子里将会有多少乒乓球呢?
抱歉——这时没有答案。这种情况下,我们已经从数学穿越到了哲学领域,所以这个问题留给你去思考、辩论。
讨论
也许你会觉得这些都太不现实,因为超级任务事实上并不可能?唔,在数学中这并不重要。我们对它们的思考、推理和研究都是可能的,数学中的许多东西都是如此。

举个例子,你相信三角形吗?它们是真实的吗?并不是。在现实世界中并没有如三角形的物体。它们只存在于我们的数学头脑中,就像无穷和超级任务以及很多其他的数学概念。我们看到的每一个“三角形”都只是一种近似——边并不完全是直的;角加起来也并不完全等于180度,等等。但这并不有损于作为一个数学实体来研究三角形和它们所有性质的重要性和必要性。
所以我们的乒乓球问题怎么跟无穷和无穷集合的数学产生联系呢?
在每种情景下,我们都在相加无穷多个球,并减去无穷多个球,但是∞-∞是无意义的:它可以有很多不同的答案,这已经为我们所证实。
乒乓球问题也阐明了两种方法之间的区别。把正整数集合和10的倍数集合分别排好并作一一对应可以表明它们是一样大的(这是布鲁斯的策略):
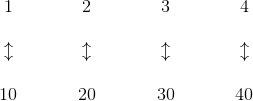
与之相对的是,从正整数集合中直接去掉所有10的倍数,留下一个无穷集合(这是克拉克的策略):
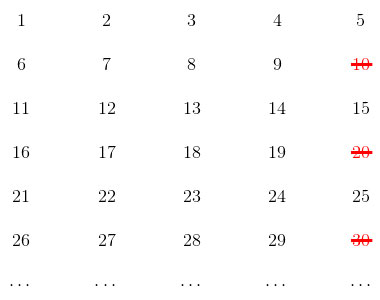
一些进一步的思考
1、 你可以尝试构造一个过程,通过在合适的时间,把克拉克的策略转变为布鲁斯的策略来使得袋子里最终留下的球数可以是任意一个指定的正整数。试试看,设计一个能够留下5个球的策略。
2、 戴安娜在参与实验的时候,球是不可区分的。考虑她的第k步放入/取出。
2.1 在这一步之后,一个随机的球还留在袋子里概率是多少?
2.2 在这一步和下一步之后,一个随机的球还留在袋子里概率又是多少?
2.3 你能用这些结果计算出在无限多步后一个随机的球留在袋子里的概率吗?
2.4 这个计算结果是否提供了一种方式,能够回答在无限多步后戴安娜的袋子里有多少个球?
2.5 在布鲁斯的情形中,他总是在取出球之前立刻放入10个球,那么最后一个球是怎么被取出以至于袋子里一个不剩?
3、 想象一下,在克拉克的袋子中有一个小妖精。当他试图取出10号球时,小妖精把数字0擦掉了,使得这个球变成了1号球;又给袋子里原本的1号球后面加了个数字0,使它变成了10号球。当克拉克取出20号球时,这个小妖精又这么做了——把20号球变成了2号,把原本的2号变成了20号。对于30、40号等等,它都如此进行。小妖精的重新标号是否意味着最终克拉克袋子里球的数量为0(就像布鲁斯一样)?
3.1 如果是,那么说清楚这是怎么回事?他取走的仍然是完全相同的那个球!
3.2 如果不是,那么最后袋子里剩下的那些球标号是什么?
4、 显然,超级任务是不可能实际做到的。那么你是否认为这些悖论表明了超级任务甚至在逻辑上都是不可能实现的?
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭