代数拓扑的数学方法正在变革脑科学

此文原载于《麻省理工科技评论》网站。

译文作者：芝城柿子芝士，哆嗒数学网翻译组成员，就读于芝加哥大学。

关注微信: DuoDaaMath 每天获得更多数学趣文

没有人彻底了解大脑各部分间的连接图全貌，但是代数拓扑的工具正逐渐帮助人们管中窥豹。

人的连接体指的是大脑中不同部分间的网络连接。这些连接表现为大脑中的白质：轴突束。轴突是神经细胞上的突起物，它们连接了组成灰质的神经细胞体。

脑科学的传统观点认为，灰质主要负责信息处理和认知，而白质负责大脑中不同部分间的信息传递。所以白质，也就是连接体，就是大脑的连接图。

人们对这个结构所知甚少，但有几个引人注目的项目正在对它进行研究。研究表明连接体比人们原来认为的还要复杂。人的大脑里有大约10的10次方个神经元，它们之间有10的14次方个突触连接。找出它们连接的方式是个极富挑战的工作，特别是因为连接体的结构取决于观察的大小尺度。

研究还发现了证据，表明白质在学习和协调大脑活动方面发挥的作用比人们所想的重要。但是这作用和连接体的结构的具体关系仍处于未知。

所以说在跨度巨大的不同尺度上了解连接体的结构是神经科学最大的挑战之一，但人们并没有合适的数学工具来研究这个课题。

如今，由于代数拓扑这个数学领域的发展，局面开始改变。这门传统上只是关于分类空间和图形的晦涩学科，现在也逐渐开始为神经科学家们所用。宾夕法尼亚大学的Ann Sizemore和她的同僚向人们展示了它如何革命性地推进了我们对连接体的了解。

代数拓扑学家的目标非常具有挑战性：他们致力于研究拓扑空间在不同尺度下的对称性。

在数学领域内，对称性指的是任何从不同的视角下看起来不变的东西。比如说正方形旋转90度后看起来没有任何变化，这就是一种对称性。

还有一些数学结构，它们在不同大小尺度下保持不变。它们被称作稳定同调(persistent homology)。寻找它们成了研究连接体的关键步骤。

神经科学家早就知道某些认知功能需要调动分散在大脑各处的许多神经节点。这些节点如何被白质连接起来的是整个连接体项目的中心问题之一。

神经科学家们通过观察水在其中的扩散来研究白质纤维。扩散核磁造影技术可以显现出水扩散的路径，从而显现出白质的结构。

为了进一步研究，Sizemore和她的同事们测量了八个健康成年人的大脑，这样他们就可以寻找在每个人大脑中都相同的结构。他们专门研究了已知在认知系统中有作用的83个区域之间的连接，这些区域包括听觉系统，视觉系统，和触觉、压力、痛感有关的体感系统等等。

这样得到了一个连接图以后，Sizemore和她的同事们运用了代数拓扑的技巧来研究它。这个新方法让他们得到了一些重要的新认识。

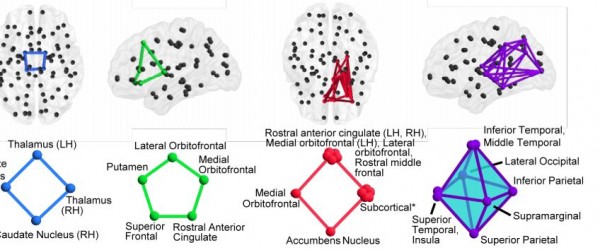
首先，它揭示了某些神经节群之间是“完全连接”的——意思是节群里的每个节点都和其他所有节点相连，整个节群组成一个叫做团的结构。所有和认知有关的系统都是由包括不同数量的节点的团组成的。

但是，研究还揭示了另一组重要的拓扑结构。这个结构叫做圈，就是闭合的环。它指的是一个节点连接着另一个节点，第二个又连着第三个，等等，直到最后一个节点连接上了第一个节点，就是一个完整的圈。

圈在大脑中产生了一个神经回路，不仅可以在大脑各处传递信息，还可以帮助反馈环作用。这些作用大概是记忆的产生或行为的控制。Sizemore和她的同事们说他们的研究发现了许许多多不同大小的圈。

不像团的范围主要局限在大脑中的特定部位比如皮质，圈的延伸范围很广。它们连接起这些功能非常不同的区域。“这些圈用一个长环连接了进化上早期和晚期出现的区域，使两者在控制脑功能上发挥的独特作用都有所降低。”Sizemore和她的同事们说。

团和圈的另一个区别体现在他们的密度。团代表了完全连接的节点，所以它们是密集的结构；环状的圈则相对比较分散。事实上，看和它们有关的大脑各部分间的所缺失的连接数量，是描述它们特点的一个方法。

圈实质上描述了连接体中的洞。Sizemore和同事们的工作表明了这些洞的作用很重要。“这些结果第一次向大家展示，代数拓扑的技巧给连接体结构的研究提供了全新的视角。这个视角把环状回路作为大脑建筑结构的关键特点。”研究团队说。

这个引人入胜的工作使代数拓扑在更好地研究连接体方面的贡献初露端倪。正如所有好的科学研究一样，这项工作不仅回答了问题，更提出了许多新问题。既然发现了圈可以比其他任何网络结构提供更多认知上的计算，那就可以问：这是些什么样子的计算呢？

另一个研究新方向是：现在的人工智能系统所依赖的神经网络是从大脑的结构中取得的灵感。既然分析发现了大脑中新的结构，人工智能领域将如何吸收这些结果，又如何在他们的工作中引入代数拓扑呢？

无疑这是一个代数拓扑学家的激动时刻。

参考: arxiv.org/abs/1608.03520 : Closures and Cavities in the Human Connectome

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文