小试牛刀:概率论击穿街头高端骗术
作者:清华大学数学系 @李逍遥易水寒
(本文由作者授权哆嗒数学网发布)
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
先来说说事情的起因。前不久,@江宁公安在线 收到微博求助,求助人在街上发现一个小摊玩掷骰子的游戏,规则如下。
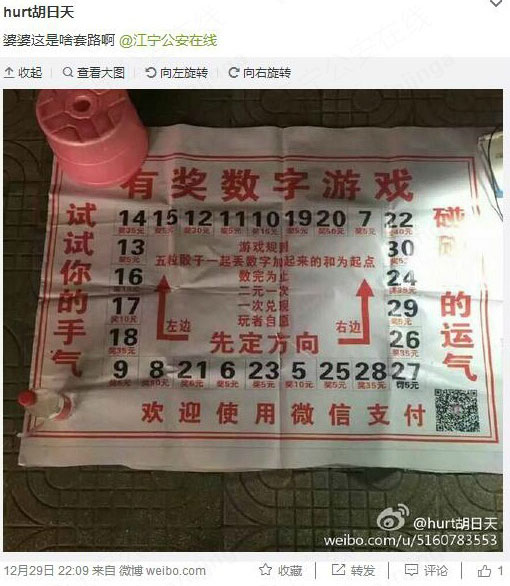
如果看不清,我们把局部放大了看。

是的,貌似只有一个是罚钱的,其他的都赚钱。好的,从经验来看这一定是个骗术,但是他骗人的机制是怎么样的呢?
我们的公安蜀黍当然不能让人民群众失望,一定要给求助者一个完整的分析。于是,做了如下分析:
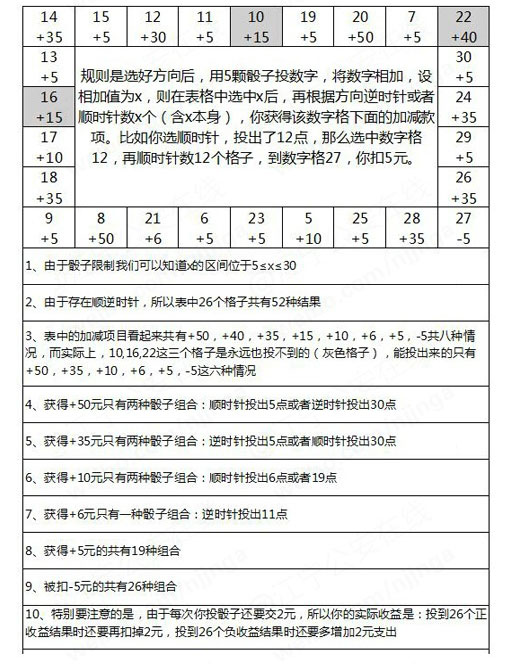
然后,蜀黍发现,他分析不下去了,貌似这并不是辣么简单的骗术,似乎骗人的手法还有点高端。于是向广大网友求助。
最后,来自清华大学数学系的 @李逍遥易水寒 给出了完整解答。 虽然,从专业数学的眼光上看,是一个简单的概率和数学期望的分析,但是解决的过程缺需要十分细心的操作。其间,还借助了软件辅助解决问题,为广大网友解惑。我们为他的这份工作点赞!
@李逍遥易水寒 的解答如下:
该游戏的26个数字布局是经过精心设计的,从而保证了利益的最大化。同时这种离散型分布而且是不具备统一的函数表达式的离散型分布,所以我们只能采用穷举加编程的方式来解决这个问题。下面的概率结果涉及到了很多细节,如果其中一个细节出错,那么最终的结果也一定会南辕北辙。第一个细节是“先交2元,然后选定方向,然后再掷骰子”。所有参与的玩家都是不清楚选顺时针和逆时针的差别,所以他们玩这个游戏的时候选方向是随机的,因此二种方向的概率都是1/2。5个骰子一共会出现6×6×6×6×6 = 7776个结果,其中有重复的情况。为了使具备高中数学水平的同学都能够看懂,本文主要采用最基础的数理方法来求解这个问题。虽然从我的角度来说很繁琐,但是从大家的角度来说将会方差便于理解整个问题,既明白结论,更重要的是能够明白问题推导的过程。
1.“中+50元”的概率:
(1)顺时针掷出5点的概率: 首先选出顺时针方向,概率为1/2;然后5个骰子都必须掷出1点,总和为5 的时候,仅存在一个情况。因此概率为1/2 × 1/7776 = 1/15552
(2)逆时针掷出30点的概率:首先选出逆时针方向,概率为1/2;然后5个骰子都必须掷出6点,总和为30 的时候,仅存在一个情况。因此概率也是1/2 × 1/7776 = 1/15552
(3)综上所述, “中50元”的概率为:1/2 × 1/7776 × 2= 1/7776 ≈ 0.000128601
2“中+35元”的概率:
与“中+50元”的情况一模一样,只是需要把顺、逆时针方向颠倒一下就可以得到这种情况。因此概率与“中+50元”一样,1/2 × 1/7776 × 2= 1/7776 ≈ 0.000128601
3.“中+10元”的概率:
(1)顺时针掷出6点的概率:首先选择顺时针方向,概率为1/2;然后掷出6点,这种情况必须要5个骰子其中一个掷出2点,剩下4个掷出1点,总共有C(5,1) = 5(C(n,m)表示n元集中选取m个元素的组合数)个情况。因此概率为1/2 × 5/7776 = 5/7776 ≈ 0.0003215
(2)顺时针掷出19点的概率:首先选择顺时针方向,概率为1/2;然后5个骰子点数相加之和等于19的可能情况的约束条件是:
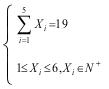 ,
,
需要通过编程来完成,结果是735种,因此概率为:1/2 × 735/7776 = 735/7776 ≈ 0.047325
(3)综上所述,“中+10元”的概率为:5/7776 + 735/7776 = 740/7776 ≈ 0.047582
4.“中+6元”的概率:
先选择逆时针方向,概率为1/2;然后掷出11点,方法同上,约束条件是: ,
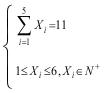
也是需要通过编程来完成,得到的结果是205种,所以“中+6元”的概率为:1/2 × 205/7776 = 205/15552 ≈ 0.013181
5.“中+5元”的概率和“中-5元”的概率:
这二种情况非常非常复杂。首先它们分别有19种和26种组合,第一步就需要先列举出来这45种组合,因为要根据每一种情况来设定约束条件,而且该游戏的设计没有按照一定的次序来进行,导致无法构造显示函数,毫无疑问又进一步加大了问题的难度。这45种组合全部计算出来之后编写程序,其中的这样才能得到“中+5元”的概率和“中-5元”的概率的准确解,没有误差的那种。下图给出的就是所有结果的概率分布,如果想要准确计算“中+5元”的概率和“中-5元”的概率,只需要将对应的情况列举出来然后累加求和即可。
|
5个骰子之和 |
对应的概率(准确值以及近似值) |
|
5 |
1/7776≈0.000128601 |
|
6 |
5/7776≈0.000643004 |
|
7 |
15/7776≈0.001929012 |
|
8 |
35/7776≈0.004501029 |
|
9 |
70/7776≈0.009002058 |
|
10 |
126/7776≈0.016203704 |
|
11 |
205/7776≈0.026363169 |
|
12 |
305/7776≈0.039223251 |
|
13 |
420/7776≈0.054012346 |
|
14 |
540/7776≈0.069444444 |
|
15 |
651/7776≈0.083719136 |
|
16 |
735/7776≈0.094521605 |
|
17 |
780/7776≈0.100308642 |
|
18 |
780/7776≈0.100308642 |
|
19 |
735/7776≈0.094521605 |
|
20 |
651/7776≈0.083719136 |
|
21 |
540/7776≈0.069444444 |
|
22 |
420/7776≈0.054012346 |
|
23 |
305/7776≈0.039223251 |
|
24 |
205/7776≈0.026363169 |
|
25 |
126/7776≈0.016203704 |
|
26 |
70/7776≈0.009002058 |
|
27 |
35/7776≈0.004501029 |
|
28 |
15/7776≈0.001929012 |
|
29 |
5/7776≈0.000643004 |
|
30 |
1/7776≈0.000128601 |
“中+5元”的概率:
共有19种组合,分别是“逆7、顺8、顺9、··· 、顺28、逆29”,其概率为1/2 × ( 15 + 35 + 70 + 126 + 305 + 420 + 651 + 735 + 780 ×2 + 651 + 540 + 420 + 305 + 205 + 126 + 70 + 15 + 5 )/7776 = 6254/15552 ≈ 0.402135
“中-5元”的概率:
总概率减去以上的所有概率得到1 – 7203/15552 = 8349/15552 ≈ 0.536844
同时我们也可以考虑采用蒙特卡洛模拟,需要编写模拟这个游戏程序去仿造这个游戏的过程(代码工作量依然不小,但是只需要将代码调试好,之后就不需要人工了),然后设定Xi = 5, 6, …, 30 , Xi的取值共有26种,这26个取值并不是均匀分布,而是呈“离散正态分布”,需要精确地算出来这26个取值的对应概率(上图已经给出了)。利用设计的蒙特卡洛算法进行模拟,比如说令i为10的9次方,也就是一亿次,虽然运算时间有点长,但是这样可以保证得到的概率值能足够精确到到你想要的任意小数点位数,结果与上述方法得到的精确值非常接近。
最后,我们给出顾客每参加一次这样的游戏所获得的期望收益值:
EX = 48 × 2/15552 + 33 × 2/15552 + 8 × 740/15552 + 4 × 205/15552 + 3× 6254/15552 + (-7) × 8349/15552 = - 32779/15552 ≈ -2.107703
意思就是当参与这个游戏顾客的数量足够多的时候,每做成一笔生意,这个老板都是净赚2.1元,次数越多,他每一笔生意的平均收入值无限接近于2.1元,同样的,顾客参与次数越多,每次都是亏损2.1元,次数愈多,每次游戏亏损的平均值无限接近于2.1元。
总结:
1、如果你想以2块钱来博取50块钱的奖金,那么要提醒你的是你梦想成真的概率只有0.0001,也就是万分之一的概率。
2、如果你不灰心,不想拿50块钱的奖金,只想拿35块钱的奖金,很遗憾,你此刻梦想成真的概率依然是万分之一。
3、如果你还不灰心,只想博取5块钱的奖金,然后去买个烤串,你的想法变为现实的概率是0.4,听起来还不错对吧。对不起,还有下面一种情况。
4、在这个游戏里面还有罚款的选项。你付2块钱有高达0.54的概率转到“-5块钱”这个选项。因此你有超过一半的概率每参与一次游戏都会输7块钱(2块钱的参与费加5块钱的罚金)的可能性。
5、综上所述,各种情况下既有赢钱也有输钱,那么通过求数学期望得到你每参加一次游戏在数学概率上都会输2.1元,参与的次数越多,你每次输钱的平均值也就无限接近于2.1元。
所以,还是老实去搬砖别想这些旁门左道了。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭