欧拉最牛的五个数学成果
原文作者: Günter M. Ziegler,柏林自由大学数学教授
翻译作者:donkeycn,哆嗒数学网翻译组成员,华东师范大学博士。
投稿可发至邮箱1178853280@qq.com,详情参见征稿说明。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
莱昂哈德·欧拉可能是史上最多产的数学家。欧拉1707年出生于瑞士的巴塞尔,但他一生中的大部分时间都是在柏林度过的。柏林的数学家们都为这一文化遗产而感到自豪。也正因为此,上个月(注:指2016年7月)在这个美丽的城市所举办的第7届欧洲数学大会有欧拉特色也不足为奇了。会上Günter M. Ziegler,一位来自于柏林自由大学的数学家以及公众参与数学的倡导者,作了一个与欧拉有关的五个著名问题的讲座。
这“五个天才的发现”之美,如Ziegler所述,在于,你不必是一个数学家就能去欣赏它们:或许要解决它们是困难的,但问题本身是容易理解且充满乐趣的。这就是为什么我们决定在这里重温它们的原因。

在这里我们不准备过多地谈论欧拉的生平(你可以在“MacTutor数学史档案”(注:原文“MacTutor History of Maths archive”)这个网站以及各种各样关于欧拉的书中找到许多有趣的信息)。值得说的是,欧拉也在俄国的圣彼得堡度过了很多时光。在那里,他育有13个孩子,在失明后完成了毕生大半的工作,并于1783年去世。欧拉曾声称“他作出一些最伟大的数学发现的时候,同时会抱着一个婴儿在他的怀里且其他孩子会围在他的脚边玩”。可悲的是,其中只有五个孩子活到成年。
现在让我们把欧拉的生平放在一边,回到那五个著名的问题上来。(这里没有注明问题的详情,有兴趣的可以百度之)
哥尼斯堡七桥问题
是否可以在该市的地图上找到一条路线,使得穿过每一座桥恰好一次?欧拉对这个问题的解答导致了图论的起源。

骑士遍历问题
是否可以连续移动一个骑士(注:骑士指国际象棋中的“马”),使得它经过棋盘上每个格子恰好一次,最后回到初始格子?欧拉是第一批系统地分析这个问题的人,但仍有一些相关问题至今还是开放的。

36军官问题
欧拉可能没有完全解决这个问题,但它导致了许多重要的工作,包括我们今天知道的数独。(编者注:36军官问题是问,从不同的6个军团各选6种不同军阶的6名军官共36人,排成一个6行6列的方队,使得各行各列的6名军官恰好来自不同的军团而且军阶各不相同,应如何排这个方队?)
欧拉多面体公式
这个关于三维物体的令人惊讶的结果告诉我们一些关于空间本质的东西。(编者注:欧拉多面体公式是指,任何简单多面体的顶点数V、棱数E及面数F间有关系V - E + F = 2)
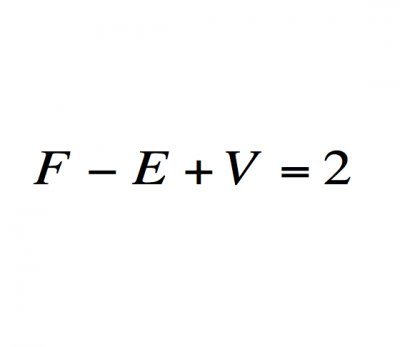
巴塞尔问题
这是一个无穷和,困惑了不少著名数学家,直到欧拉找到了令人惊讶的答案。
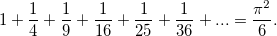
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

评论已关闭