拆解一个极限的前世今生

 

作者： 季真俊，就读于华东师范大学。

 

投稿可发至邮箱1178853280@qq.com，详情参见征稿说明（截止日期延期至4月28日）。

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 在同学刚刚步入微积分时，相信有很多人都会在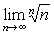这一个极限上摸不着头脑：这是一个的“∞的0次方”形式的未定式，因此常规的四则运算都对其无济于事。

在华东师范编写的第四版数学分析上，给出了两边夹的做法：

 

 

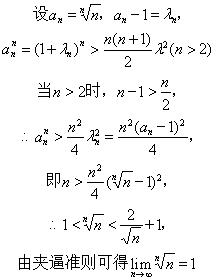
可这个证明有些让人有点摸不着头脑，下面我们就来介绍这一个极限的由来：

引理1：

 

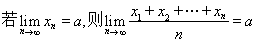
证：

 

 

令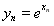，则可以得到以下结论：

 

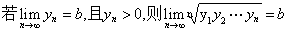
引理2：

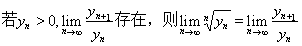
再令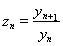，则又可以得到以下结论：

引理3：

 

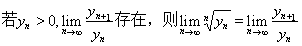
再来看我们一开始提出的那个问题：求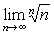，由引理3可直接得到

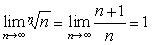
而且还可以得到这个极限的加强形式：

 

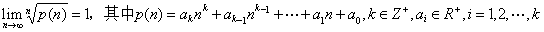
当然，有些了解stolz定理的同学也会说，这个极限完全不需要这么麻烦，取对数之后使用stolz定理，也可以直接得到答案。

不错，但是如果我们认真研究一下引理1和stolz定理的关系，则不难发现引理1的逆命题便是stolz定理的一个特殊情况，而在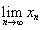与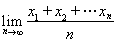均存在的情况下，引理1及其逆命题是互相等价的。因此我们并不需要用上stolz这把“牛刀”去宰一只鸡，而仅仅使用其一个特殊情况就够了。

除此以外，也可以先对其取对数后利用归结原则将数列极限转化为函数极限以后洛必达求解。

下面我们考察这个极限的一个变型：
 

 

例：求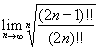，其中，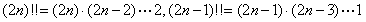

方法一：

 
方法二：

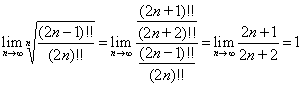
以上两种方法虽然本质相同，但由于处理原式的技巧不同，其繁简度亦有很大差异，因此我们在思考问题时同样要注意：是否有更快的捷径？

 

 

微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa