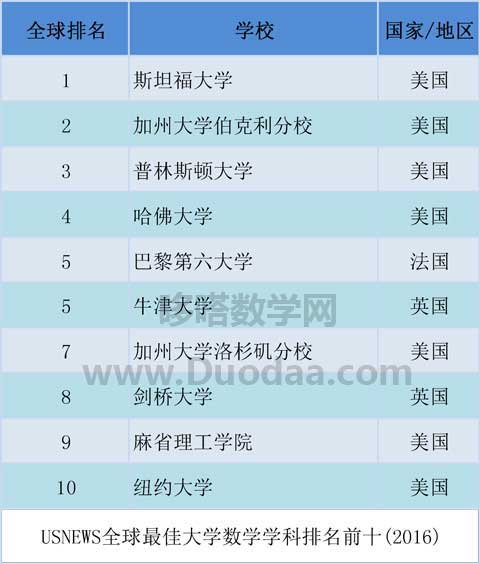
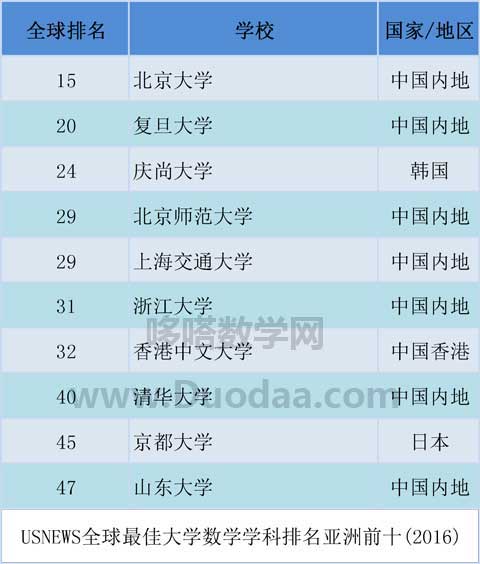
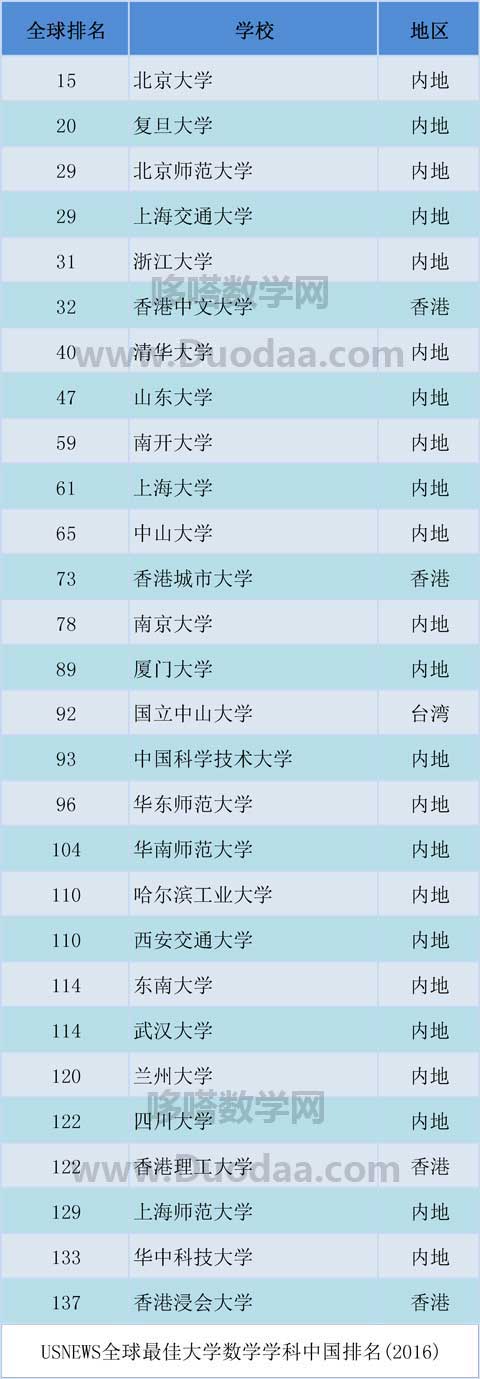
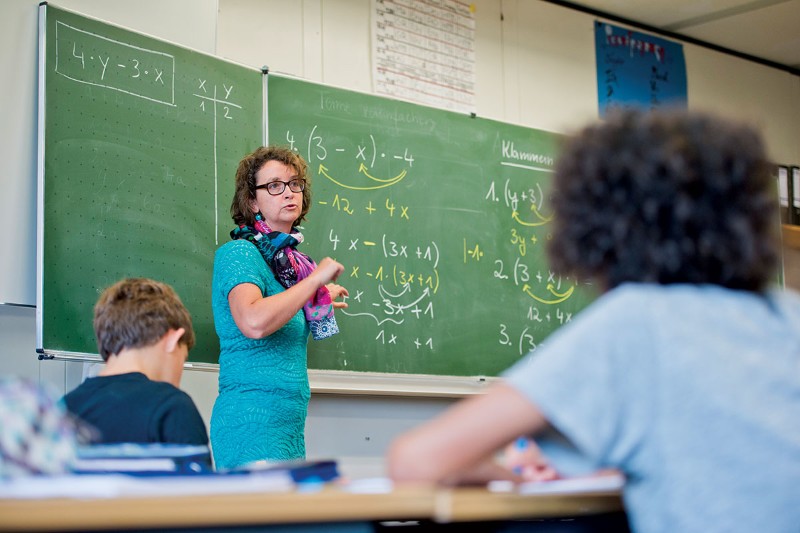为什么要学数学? ——《给年青数学人的信》第一封
作者:伊恩·斯图尔特,英国沃里克大学数学教授,因其大量优秀的数学科普作品而响誉世界。
《给年青数学人的信》是作者伊恩·斯图尔特尝试部分更新《一个数学家的辩白》,也就是说,更新那些或许会影响一个年轻人的决定,如考虑取得数学学位和可能的数学专业生涯。这些给“梅格”的信件大致遵照时间先后,从她高中一直写到在大学获得永久教职为止。书中讨论许多的议题,包括最初关于职业生涯的决策到职业数学家的工作哲学,以及数学家研究题材的本质,不只有一些实在建议,还提供来自数学圈子内的见解,并且解释数学家到底在做什么。
关注微信:DuoDaaMath 每天获得更多数学趣文
第一封信 为何学数学?
亲爱的梅格!
或许如你所预期,得知你考虑攻读数学时,我非常高兴。不只是因为数个夏天前,你用数星期反复阅读《时间的皱纹》(A Wrinkle in Time)的时间并未白费,同时也不枉我费心对你解释超立方体和高维空间。我不依顺序回答你的问题,先回答其中最实际的问题:除了我以外,有谁真的靠数学维生?
这个问题的答案和许多人所想的不一样。我所服务的大学在几年前对校友进行调查,发现在种种学位之中,有数学学位的人平均收入最高。需要提醒你的是,虽然这是在他们成立医学院之前的事,但至少驳倒一项谬论:学数学的人无法拥有高收入的工作。
事实是我们每天到处都可遇到数学家,只是很难察觉而已。我过去的学生有的管理酿酒厂、创立他们自己的电子公司、设计汽车、编写计算机程序和在股票市场交易期货,我们几乎从未认识到银行经理或许拥有数学学位,发明和制造DVD和MP3播放器的人们中有很多是数学家,或是将木星卫星令人惊异的照片传输至地球的技术里也包含大量的数学。我们知道医生有医学学位,律师有法律学位,因为那些是特殊和明确定义的专业,要求同等专业的训练。但人们不可能在建筑物的铜制铭牌上发现有证照的数学家的名字,替该数学家打广告:这位数学家在获得一大笔费用后,可以帮忙解决想要解决的任何数学问题。
我们的社会消费了大量的数学,但一切只在幕后进行,原因相当直接:数学属于幕后。当驾驶一辆汽车,你绝对不想考虑所有那些复杂的机械方面的东西,只想钻进车子里将它开走。了解车子机械的基本状况,当然对你成为好的驾驶员有所帮助,但绝不是一定要这样才行的。同样地,数学也是如此。你希望车子的导航系统引导方向,而不需自己来计算所涉及的数学。此外,你希望即使不了解信号处理和误差修正码,你的电话仍可以运作。然而,我们其中的一些人需要知道如何运算数学,否则上述的汽车和电话将无法运作。如果其他人能够了解我们日常生活是如何必须依靠数学,那将是一件好事。为何将数学远远放在幕后,这是因为许多人完全不知道数学藏身在幕后。
我有时觉得,要改变人们对于数学的态度,最好的方式是,在任何用到数学的东西上贴上写着“内含数学”的红色标签。当然在每一部计算机上都会贴上一张,又如果照字面的解释,我们也应该在每一位数学老师身上贴上一张。我们也应该将红色数学标签贴在每一架飞机、每一部电话、每一辆车、每一个交通标志、每一种蔬菜……
蔬菜?
是的。农夫只是照着他们父亲和祖先流传下来的模式耕种,这种日子早已过去。几乎所有你能买到的蔬菜,都是长期和复杂商业培植计划的结果。“实验设计”数学意义上的整个主题,在二十世纪早期被发展出来,用来提供一个系统的方式去评估新种的植物,遑论基因修改的较新方法。
等等,这不是生物学吗?
当然是生物学,但也是数学。基因学在生物学里最早使用数学,人类基因组计划之所以成功,不只是因为生物学家做了许多明智的工作,也因为发展出强大的数学方法,用以分析实验结果,并且从非常破碎的数据里重建准确的基因序列。
所以,蔬菜得到一个红色标签。如同蔬菜,其他东西也应贴上一个红色标签。
你看电影吗?你喜欢特效吗?《星球大战》(Star Wars)和《魔戒》(Lord of the Rings)里面有数学? 最早的完全计算机动画电影《玩具总动员》(Tory Story),促成了大约二十篇数学论文的发表。“计算机绘画”不只是使用计算机来做画,也是让图画看起来更真实的数学方法。为了做出这些效果,需要立体几何的知识、光的数学,以及在起始和完成的影像间内插一连串平滑的动作,等等。“内插”是一个数学的想法,如果没有许多聪明的数学,内插将不会产生作用——又一个红色标签!

当然还包括因特网,完全是数学运作。目前最主要的搜索引擎Google使用数学方法,根据矩阵代数、概率理论和网络的组合数学,去寻找最可能包含用户所需信息的网页。
但因特网的数学较这些更为基本。电话网络依赖数学,它不像旧时,当时接线生必须手动将电话线路插入总机,而今天这些电话线必须同时传输数百万个信息。有太多人想要和朋友谈话、传真或上网,以致我们必须分享电话线、海底光缆和卫星中继器,否则网络无法承受那么繁忙的交通。所以每一段谈话都被分解成数千个小段,只有约1%的小片段被实际传输,其余的99%借着填补间隙的方式尽可能地被复原(之所以行得通,是因为取样虽短但频率非常高,以致你声音的改变比取样的间距来得慢很多)。噢!整个信号被编码,以致任何的传输错误不仅可被检测出来,也可重新放到正确的接收位置。
如果没有大量的数学,现代通信系统将无法运作。编码理论、傅立叶分析(Fourier analysis)、信号处理……
总之,你上网购买机票、订位、前往机场、坐上飞机后飞往他处。飞机之所以能够飞行,是因为工程师使用流体流动和空气动力学的数学进行设计,确保飞机可以飞在天上。飞机使用全球定位系统(简称GPS,定位系统由一组卫星构成)来导航,卫星信号经由数学分析,可以在数英尺的误差内告诉你飞机的位置。每一个航班都必须列入时间表,才能让每一架飞机处于正确的位置,这需要其他领域的数学。
亲爱的梅格,这是数学运作的方式。你问我数学家是否都隔绝在大学里,或是否有部分数学家的工作和实际生活有关。其实你实际生活的全部,就如同一艘在数学海洋里徜徉的小船,上下摆动。
但很少有人注意到这一点。逃避数学会让我们感到自在,但却贬损了数学。这真可耻,这样一来,人们认为数学没有用处、不必在意,数学只是智力游戏而已,没有真正的重要性。因此,我才想要看见那些红色标签。事实上,不用红色标签的最佳理由,是大部分的地球都将被红色标签所覆盖。
你的第三个问题最为重要,也最令人哀伤。你问我是否必须放弃对美的感受以研读数学,是否所有事情将变得只剩下数字、方程式、定理和公式。梅格,敬请宽心,我不会怪你问这个问题。可惜这是个非常普遍却错得离谱的想法,和真相恰好相反。
数学对我而言如下:它让我以全新的方式知觉这个我所居住的世界,让我对自然的定律和模式开了眼界,并提供全新的关于美的经验。例如,当我看见彩虹,我不仅是看到一道光亮多彩的圆弧,也不仅是看到雨滴对阳光的影响,雨滴将白色日光还原为构成日光的色彩成分。我发现彩虹既美丽又启发灵感,对彩虹不仅只是光线的折射而心存感激,这些颜色就像红色(还有绿色和蓝色)的鲱鱼。彩虹的形状和亮度需要解释:为何是圆弧状? 为何光线如此之亮?
或许你尚未想过这些问题。你已经知道,当阳光受到雨滴的折射时会出现彩虹,因为阳光的每一种颜色会朝稍微不同的角度转向,并从雨滴反射进入我们的双眼。但事情不是如此简单,为何数以万计雨滴折射产生的数以万计有色光线,不会重叠并模糊掉呢?
答案在于彩虹的几何学。当光线在雨滴内部进行反射,雨滴的球状形体导致光线聚焦于某一特定方向,每一滴雨滴发射出明亮的圆锥形光线,或是说每一种颜色的光形成自己的圆锥体,而每一种颜色形成之圆锥体的角度稍有不同。当我们望向彩虹,我们的眼睛只能侦测到位于特定方向的圆锥体,每一种颜色的方向在天空形成一个圆弧。所以我们看到许多同心圆,每一种颜色形成一个同心圆。你所见到的彩虹和我所见到的,是由不同的雨滴所形成。我们的眼睛位于不同的位置,所以我们侦测到由不同的雨滴所产生的不同圆锥体。
彩虹是个人经验。
某些人认为这样的理解会“破坏”情感的体验,因为它会产生对美感满足的某种压抑,但我认为这是无聊的想法。做这样声明的人通常喜欢假装自己充满诗意,对世界奇妙事物抱持开放的态度,但事实上他们严重缺乏好奇心:拒绝承认世界比他们自身的有限想象来得更奇妙。自然永远比你所想的更深邃、更丰富、更有趣,数学提供你一个非常有用的方式去欣赏自然的美。理解的能力是人类和其他动物最大的不同,我们应该珍视。许多动物都有情绪,但只有人类能理性思考。我必须要说,我对彩虹几何学的理解,为它的美增加了新的光彩,而情感的体验却一点也不会因此变少。
彩虹只是一个例子。我观察动物也和常人的角度不同,因为我注意到动物移动时对应的数学模式。当我注视一块水晶,我留意到原子晶格和外在色彩的美丽。在波浪、沙丘、太阳起落、雨滴落在水坑溅起涟漪,甚至停在电话线上的鸟,我也都能看到数学。此外,如同望向弥漫大雾的海洋,我模糊了解到,这些日常奇妙的事物充满无限的未知。
数学的内在美丽也不应该被轻视、被忽略,数学研究本身就已非常美丽优雅。数学的内在美并不是我们在学校里使用的“加法”。虽然加法背后的一般原则自有其美丽之处,但它们大多难看又无定形。数学的内在美丽存在于:想法、普遍性、突然一闪而过的灵感,以及使用直尺和圆规尝试三等分某个角度就等同于去证明3是一个偶数;我们无法建构一个等边七边形,但可建构一个等边十七边形;没有方法可以解开单结;为何某些无限大比其他还大,而某些应该较大的无限大结果却相等;等于连续平方之和(1+4+9…)的唯一平方数为4900(1除外)。
梅格,因为你有一个合乎逻辑和追根究底的心灵,你有成为优秀数学家的潜力。你不会满意于模糊的论点,你想要看到细节并亲自检查,你不只是想知道如何让事物运作,而且也想知道为何事物能够运作。此外,你的来信让我企盼,将来你能和我目前一样,能够看到数学的有趣和美丽——以一种独特的看待世界的方式。
我希望,这为你研读数学建立了所需要的背景。
关注微信:DuoDaaMath 每天获得更多数学趣文