从一到无穷大:对应与计数
作者: 桃夭灼灼。
投稿可发至邮箱1178853280@qq.com。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文
一、伽利略的疑惑
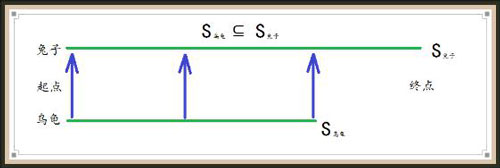
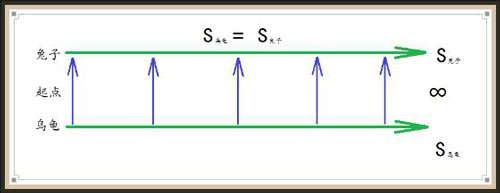
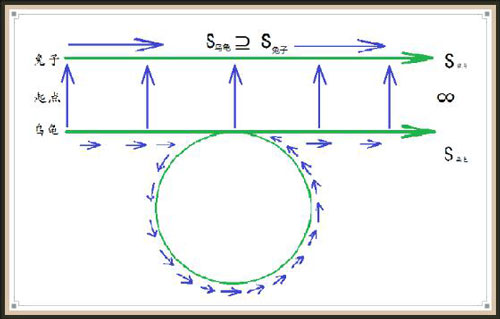
物理学家伽利略曾提出这么一个问题。我们知道任何一个偶数都可以写成2n(n为自然数)的形式,因此对于任何一个自然数n,都可以将它乘以数字2而得到一个偶数2n。此外,如果有两个不同的自然数n和m,按照上面的方式可以得到两个不同的偶数2n和2m,换句话说,不可能有两个不同的自然数对应着同一个偶数。现在的问题是,按照这个方式,可以将自然数和偶数作一对一的对应,同时表明自然数似乎和偶数是一样多的。但是直觉告诉我们,偶数只是自然数的一部分,或者仅占自然数的一半,因为还有另一半是奇数。
伽利略对于这个问题思考很久,但无法给出令人满意的结果。在此之后的两百年间,数学家对于涉及到无穷大的问题,总是以“比任何数都大”的方式处理。
二、康托的解答
19世纪,数学家康托作出这么一个设想:如果我们承认自然数的确是和偶数一样多,那会带来什么样的影响?
要承认这个事实,首先从有限多个事物开始说起。比如有五个苹果装在篮子里,有五本书放在书架上,我们的第一反应是它们的数量都是5,但我们忽略了一个过程,我们是用阿拉伯数字5来表达这个结论。可是,一旦停止使用任何一种计数方式(如阿拉伯数字,罗马数字等),我们的想法仍然认同它们一样多,因为可以给这五个苹果和五本书贴上不同的标签,比如用大写字母ABCDE表示五个苹果,用小写字母abcde表示五本书,然后让每一个大写字母与相应的小写字母对应,这样五个苹果和五本书是一样多的。
此外,对于五个苹果和七本书,可以肯定它们是不一样多的。更进一步,只要所研究的问题中事物数量是某个自然数,类似于上面贴标签的方法,总能得出谁多谁少的结论。但是语言文字中使用的字母、符号总是有限(例如英语有26个字母,俄语有33个字母,日语有71个假名),而对于事物数量稍多一些的整体,却无能为力,因此数字起到了一个非常重要的作用,其中自然数的引入帮助我们自动完成了这么一个一对一的贴标签过程。
接下来考虑这么一个事实。如果事先有100个人,旁边还有一堆书,但不知有多少,现在让每个人都拿一本书,最终正好拿完,并且没有一个人会拿走两本书,也没有一个人没有书,那么一定有100本书,自然不需要一本一本地去数。
如果实现的人数也不知道,当然我们还是不知道有多少本书,但仍然可以肯定,人数和书本的书目是一样多的,尽管我们对于其中的数量一无所知。这个事实表明:由人所构成的集体与由书本所构成的整体之间的个数相同。
总之,只要所研究的问题中事物数量是有限,那么一定可以建立一个一对一的对应来确定谁多谁少,而无需知道有多少和是多少。这个结论给予我们一个启发:对于涉及到无穷多个事物的两个整体,能否用类似的方式来区别这两个整体所含有事物数量是否有差别?但是要注意,在无穷多个事物组成的整体中,已经不能用“数量”或“个数”的概念。
康托对此给出了一个令人满意的结果。他认为凡是有无穷多个事物的一个整体,可以用“势”(“基数”)来描述这个整体中所含有事物的多少。当然,对于一个数量有限的整体,势就是它所含有事物的个数。其次,对于两个整体A和B,只要能在A和B之间建立起一个一对一对应,而不管A和B究竟有多少(即使有无穷多个),我们就认为他们有相同的势。例如,取A为全体自然数,而B是全体偶数,根据开始给出的对应方式,A和B有相同的势。这样自然就解决了伽利略提出的问题,但它打破了我们的常识性认识,即欧几里德在《几何原本》一开始就提出的规定:整体比部分多。
对于集合中元素的“个数”,如果可以用一个具体的数字来表达,则称这个集合是有限集,反之,如果找不到一个具体的数字来表达“个数”,或者说集合中元素的“个数”比任何一个自然数都大,则称这个集合是无限集。对于有限集,在组合数学中有广泛研究。对于无限集,根据康托的思想,将无限集中元素的“个数”称为“势”。两个无限集A和B之间如果有一个一一映射(既是单射又是满射),则这两个集合有相同的势,称为对等的。
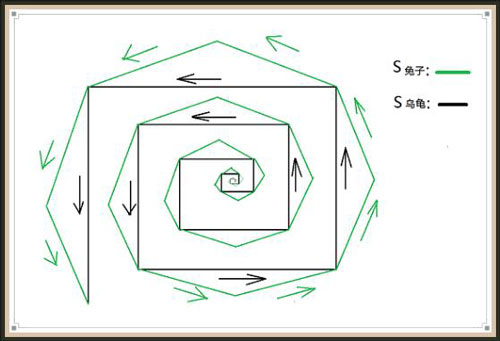
对于全体偶数组成的集合,显然和全体自然数组成的集合有相同的势,当然还有很多集合与全体自然数组成的集合有相同的势,例如分数和自然数一样多,有理数和自然数一样多。为此,规定全体自然数组成的集合的势为“阿列夫零”。这个称呼来自于希伯莱字母“阿列夫”,其原因或许在于数学家康托是犹太人。如果一个无限集的势为阿列夫零,称为可数集,反之一个无限集的势不是阿列夫零,称为不可数集。除了阿列夫零以外,康托还为我们规定了阿列夫一、阿列夫二、阿列夫三……等无穷多种势,同时他得出了一个重要的结论:任何一个集合的幂集(即它的一切子集构成的集合)的势都大于这个集合的势。这就说明没有最大势。
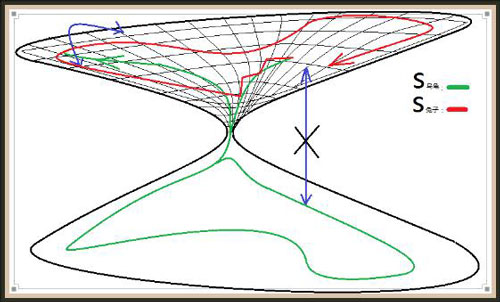
此外,康托首先看到了一个自然而重要的问题:在阿列夫零和阿列夫一之间是否存在一个中间势?他并没有解决这个问题,但他相信没有这个中间势。这就是著名的康托连续统假设。这个假设现在终于被人们搞清楚了,它可以作为一条公理,并且与集合论中其它一些公理是独立的。
三、希尔伯特旅馆
在1900年第二届国际数学家大会上,希尔伯特把康托的连续统假设列入20世纪有待解决的23个重要数学问题之首,他本人则提出了一个有趣的故事。
有一个旅馆,我们称它为希尔伯特旅馆。第一天来了一位客人要求入住,但老板表示已经客满,不过老板想出了一个方法。首先,他让一号客房中的客人搬出,让外面等待的客人入住一号客房。然后让二号客房中客人搬出,让原先一号客房中的客人入住二号客房,再让三号客房中的客人搬出,让原先二号客房中的客人入住三号客房。依此方式,最终让每个客人都有自己的客房(包括新来的客人)。
第二天,又来了一些游客,人数大约在100人左右,旅馆老板表示已经客满,不过聪明的老板又想出了一个方法。首先安排第一个游客入住,所作的安排与第一天入住的客人所作的安排一样。待第一个游客住下,又安排第二个游客入住,所作的安排与第一个游客所作的安排一样。最后,依次安排第三个、第四个游客直至最后一个游客入住。第三天,又有很多游客要求入住,人数无法确定,总是有无穷多人,老板表示已经客满,但他有方法可以让每个客人有自己的客房。
我们暂时不去关心老板最后的安排,这个故事被数学家们称为希尔伯特旅馆,借此他引出数学上的“可数无穷大”概念。与现代图论结合,又产生了网络枢纽无堵塞观点。
四、尾言
自康托提出连续统假设以来,数学家一直致力于解决这个问题。但不久人们就在康托的集合论中发现了悖论,为了消除这些悖论,就开始对集合论进行公理化处理,并先后尝试建立了几个集合论公理系统。人们通常使用的是策梅洛和弗兰克尔建立的ZFC公理系统。进行公理化后,基本上都能消除悖论。1938年哥德尔证明了连续统假设和ZFC公理系统不矛盾,两者是协调的。1963年美国数学家科恩又证明了连续统假设和ZFC公理系统是彼此独立的,是不可能判定真假的。这样在ZFC公理系统中,连续统假设是不可能判定真假的,这是60年代集合论的最大进展之一。正如帕斯卡比喻的那样:人只是漂浮在无限和虚无这两个无底深渊之间的一叶扁舟,我们总想要追求某种确定性,但却永远也抓不住,一不小心我们的整个基础就会分崩离析,而下面就是那无底深渊。在数学上,人永远只是探索者,没有“终结者”。
微信、手机QQ搜索关注 DuoDaaMath 每获得更多数学趣文

作者: 桃夭灼灼。
投稿可发至邮箱1178853280@qq.com。
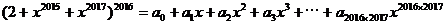 ,那么
,那么 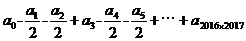 的值是多少?
的值是多少?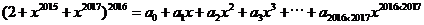 ,所以常数项容易求,在等式两边令x=0,则有a_0 = 2^2016。但是右边会出现一次项二次项吗?笔者感觉x的最小指数应该是2015,貌似a_1, a_2, ……, a_2014应该为0。
,所以常数项容易求,在等式两边令x=0,则有a_0 = 2^2016。但是右边会出现一次项二次项吗?笔者感觉x的最小指数应该是2015,貌似a_1, a_2, ……, a_2014应该为0。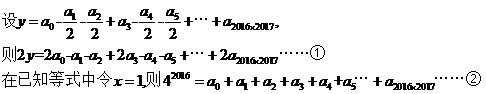
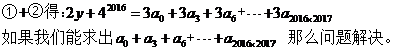
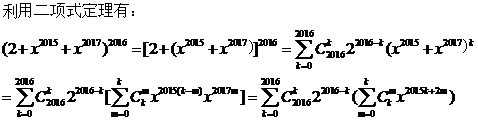
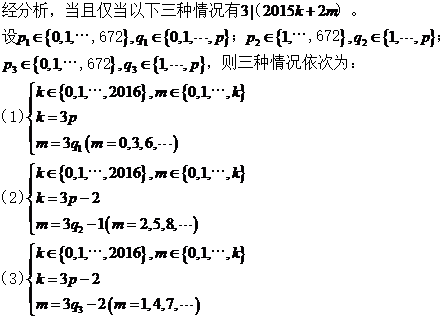
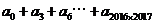 ,所以
,所以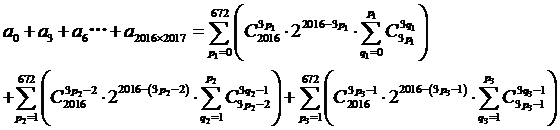
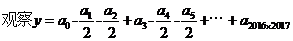 ,三个一组三个一组,每组中连续出现两个-1/2 ,太奇怪了。由【疑问一】、【疑问二】可知,用常规的实数0,1赋值不可能有这种效果出现。想想我们所见过的成千上万不计其数的数,实数也好虚数也罢,哪一个数的整数次幂会以3为周期,并且同时含有系数 ?
,三个一组三个一组,每组中连续出现两个-1/2 ,太奇怪了。由【疑问一】、【疑问二】可知,用常规的实数0,1赋值不可能有这种效果出现。想想我们所见过的成千上万不计其数的数,实数也好虚数也罢,哪一个数的整数次幂会以3为周期,并且同时含有系数 ?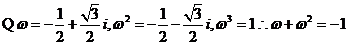
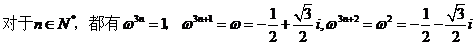
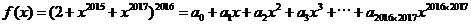
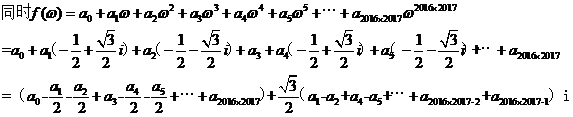
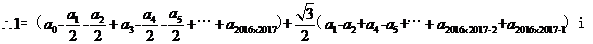
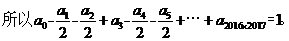
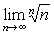 这一个极限上摸不着头脑:这是一个的“∞的0次方”形式的未定式,因此常规的四则运算都对其无济于事。
这一个极限上摸不着头脑:这是一个的“∞的0次方”形式的未定式,因此常规的四则运算都对其无济于事。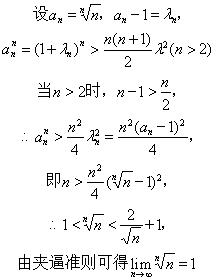
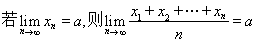

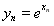 ,则可以得到以下结论:
,则可以得到以下结论: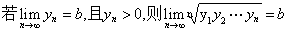
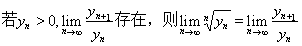
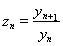 ,则又可以得到以下结论:
,则又可以得到以下结论: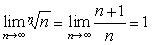
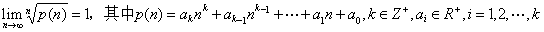
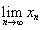 与
与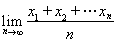 均存在的情况下,引理1及其逆命题是互相等价的。因此我们并不需要用上stolz这把“牛刀”去宰一只鸡,而仅仅使用其一个特殊情况就够了。
均存在的情况下,引理1及其逆命题是互相等价的。因此我们并不需要用上stolz这把“牛刀”去宰一只鸡,而仅仅使用其一个特殊情况就够了。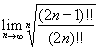 ,其中
,其中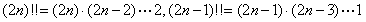 ,
,