微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

数学世界里有很多著名的难题，比如歌德巴赫猜想。歌德巴赫猜想作为一个世界难题之所以著名，是因为问题本身太容易表达了，表达出来后，一个小学生都能看懂。如果，把这个样的问题放在教材课后的习题部分，不知道能坑掉多少脑细胞。

然而，数学就是这么神奇，一些数学问题的表述非常简单，简单得就像课后的习题一样。但要解决他们非常困难。就像他们故意伪装成课后习题似的。下面的10个问题大概就是这样的问题。他们的表述非常简单，普通大二的理工科学生都能看懂，但至今无人能解决。

 

第十名  数一数，素数和合数到底有多少的问题

习题伪装指数：☆

 

如果学过初等数论，我们由素数定理可以简单的认为素数在自然数中的密度为零。那么我乱扔一个其他形式的一堆自然数，其中素数的密度也是零吗？

 

问题：形如2^n+5的自然数几乎都是合数。( 2^n表示2的n次方，几乎的意思是指密度为1 )

 

好吧，看懂这个似乎要至少学过初等数论。但是不是所有理工科的朋友都学过这门课。但这个问题真的很难，至今不知道怎么解决。

 

第九名  看上去是线性代数中找几组基的问题

习题伪装指数：★

 

线性代数相信大多数理工科的朋友都会学习。我相信，对线性空间这个名词并不陌生。对于n维线性空间，任意n个线性无关的向量都能组成该空间的一个基。现在，我们有B1,B2,...,Bi,...,Bn这n个向量组（wiki上要求两两不交，其实不要求也可以），每个向量组有n个向量，这些向量组都构成n维线性空间的一个基。于是这里，有n×n个向量。现在，把这个n×n个向量排成一个n×n矩阵，矩阵的第i行的n个元素，正好是Bi中的n个元素（这一行的顺序无所谓）。

 

问题：对任意给定的n个基，有没有一种排列办法，满足上述条件，而且矩阵中的每一列的n个向量都构成线性空间的一个基。

 

这个叫做罗塔基猜想，由罗塔在1989年提出。这其实是一个披着线性代数外衣的组合问题。这里只是提到它的线性代数版本，还有别的版本，比如流形版本。

 

 

第八名  一个忧伤故事引发的数学难题

习题伪装指数：★☆

 

一个忧伤的故事，有n个人(n>1)在半径为1千米的圆形跑道上匀速的跑圈，没有人静止不动（即速度大于0）。他们出发点相同，行走的方向相同，但没有任何两个人速度是相同的（就是说，n个人的速度两两不同）。跑道上的人感情很脆弱，当一个人和其他每个人的距离都大于等于1/n千米的时候，这个人会觉得自己很孤独。

 

问题：请证明对任意n，跑道上的人每一个人，都有孤独的时候！

 

这叫做孤独的跑者问题。这个问题非常难，目前的情况是，有人证明了n≤7的时候，命题成立。另外，陶哲轩证明了，对任意的n，只需要验证有限多种情况就可以判定命题是否成立。但就仅n=8的时候，那个分类的带来的计算量，已经不是地球上的计算机能处理的了。

 

第七名  集合求并集，找元素的“小问题”

习题伪装指数：★★

 

关于集合的知识，我们在高中就学了不少了。一个集合也可以是另外一个集合的元素，比如集合{{2,3,4},{1,4,6,9},{1,2,3,4,6,9}},{2,3,4}就是它的一个元素。一个由集合为元素组成的集合我们称为集族。如果一个集族里面任意两个元素并起来，还是这个集族里的元素，我们就说这个集族对并集运算封闭(因为集族里的元素都是集合，于是可以做并集运算)。

 

问题：一个有限的集族，集族的每个元素也都是有限集合。如果它对并集运算封闭，且不是{∅}，那么是否一定有个元素，这个元素属于集族里至少一半的集合。比如，前面举的集合例子，它是一个3个集合组成的集族，而元素2是第一个和第三个集合的元素，超过3的一半。

 

此问题由彼得·弗兰克尔在1979年提出，叫做并集封闭集族猜想。快40年了，没人解决。目前的情况是，人们解决了集合数量不超过46个的集族的情况，以及集族中最少元素不超过两个的情况，这些时候答案都是肯定的。

 

第六名   一个求极限的问题，判定出来的极限值是什么

习题伪装指数：★★☆

我们的很多读者一定做过这样的习题，就是证明 1 + 1/2 + 1/3 + 1/4 + ...+ 1/n - ln(n) 在n→∞的时候，极限是存在的。用的办法是单调有界原理。我们把这个极限用符号γ表示，称作欧拉常数。

 

问题：判断欧拉常数γ是有理数还是无理数。

 

我们知道他的近似值，0.57721566490153... ，2003年有人用从对它的连分数研究中得到结果是：如果欧拉常数是有理数，那么它的分母将超过10的242080次方。但是依然离判断出结果很远。

 

第五名  貌似小学生都“知道”的有理数无理数问题

习题伪装指数：★★★

 

自然对数底e，圆周率π都是我们在中学里最常见的无理数。上了大学学习了高等数学或者数学分析后，我们有能力证明他们是无理数这件事情当然可能需要一些课外阅读)。但是我们对这两个数做四则运算后的结果，是有理数还是无理数却并不知道。

 

问题：判断e＋π和eπ是有理数还是无理数。

 

这个问题似乎没看到希望。不过，你可以用韦达定理和e、π是超越数的事实，轻易的判断e＋π和eπ不可能都是有理数。

 

第四名   好“简单”的级数敛散性判断“作业题”

习题伪装指数：★★★☆

 

我们在高等数学里学了很多种级数敛散性的方法。给一个看上去形式简单的级数，判断它收敛怎么看都是课后习题级别难度的问题。那么我们看看下面一个级数。

 

 

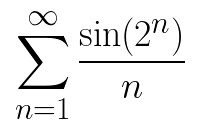
问题：上面的级数是否收敛？

 

这个问题其实是一个和π有关的数论问题。实际上很多看上去带sin的极限问题都是伪装成高等数学的超越数论问题，都和π有关系。

 

第三名   关于正整数乘乘除除的游戏

习题伪装指数：★★★★

 

我们来做一个游戏。给你一个正整数，如果它是偶数，我们把它除以2得到一个新的自然数，如果新的自然数还是偶数，继续除以2。这样一直除到他是奇数为止。对于这个奇数，我们把它乘以3再加上1，这样又得到一个偶数。我们再继续前面的操作——只要是偶数就除以2，奇数就乘以3加上1。这样一直操作下去，我们会得到一个无穷长度的正整数序列。

 

问题： 对任意给定的初始正整数，按上面操作的得到序列最终会归于4,2,1,4,2,1,4,2,1,... 的循环？

 

这叫做考拉兹猜想，也叫3n+1猜想。有人把这个问题作出了推广，有了这个猜想的推广版本。已经证明推广版本的猜想是一个算法不可判定问题——简单的说，不可能用计算机程序来证明推广版本的猜想。

 

第二名   把分数拆成分数单位的“小学奥数”题目

习题伪装指数：★★★★☆

 

我们小学就学习分数了。记得小学的奥数题目里，经常干一件事情，就是把一个分数拆成几个分数单位的和。下面的问题也和这个有关系。

 

问题：问题：对任意大于1的正整数n， 关于x,y,z的方程 4/n = 1/x + 1/y + 1/z , 是否都有正整数解？即4/n都能正好拆成三个分数单位的和。 

 

这个问题叫做埃尔德什-施特劳斯猜想，1948年提出，已经快70年了。注意到 4/5 = 1/2 + 1/4 + 1/20 = 1/2 + 1/5 + 1/10，有两种写法。于是有人转而研究满足方程解的个数的规律（注意，如果有个n对应的解的个数是0，就否定了这个猜想）。2013年的结果是，解的个数相对于n的增长速度是不超过关于ln(n)的多项式级别的。

 

第一名 “非常简单”的不等式，但结果令人意外

习题伪装指数：★★★★★

 

诉说这个问题前，我们来看看这样两个函数。对于一个正整数n，我们把它所有的约数加起来，得到的正整数记为σ(n)。比如24的约数为1,2,3,4,6,8,12,24，那么σ(24) = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60。 同样是正整数n，我们把不大于它的所有正整数的倒数加起来，记为H(n), 就是说H(n)=1 + 1/2 + 1/3 + ... + 1/n . 比如H(3)= 1 + 1/2 + 1/3 = 11/6 。 通过σ(n)和H(n)我们构建如下的不等式：

 

 

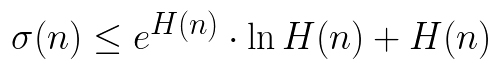
问题：对所有正整数n，是否都有上面的不等式成立。

 

如果我告诉你这个不等式问题是很多数学家心目中在整个数学界最重要的猜想，你信吗？2002年，一位数学家证明了此不等式与大名鼎鼎的黎曼猜想等价。也就是说，证明了这个不等式，也就证明了黎曼猜想。而黎曼猜想在数学界的地位，大家自行百度吧，至今还有人悬赏100万美元征解。黎曼猜想的原始版本，需要有复变函数的学习背景才能看懂，但这个版本，估计中学生都能看懂了。

 

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

原文作者：Rebecca Hills-Duty。 

译文作者：Jessie仪，哆嗒数学网翻译组成员，就读于布里斯托大学。

 

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

俄克拉荷马州立大学和佐治亚理工学院的数学家们正在尝试为生活带来一个不同的世界：通过创造一个虚拟现实空间来探索那些我们所熟知的规则无法实现的“另类几何学”

 

在我们平时所学的一般几何学中， 两条平行线永远以相同的距离延续，从来不可能靠近或者远离对方。然而在非欧几里得几何中，同样的平行线最终会相交，或者改变方向渐渐远离。

 

 

佐治亚理工学院的Eilsabetta Matsumato与俄克拉荷马州立大学的Henry Segerman日前正在研究一个叫做“双曲VR”的项目，该项目旨在共同努力来向大众科普双曲几何学——一种两条平行线可以渐渐发散的非欧空间。Elisabetta Matsumato说：“你当然可以想象出这种现象，但是你很难切身感知它，直到你真正体验到了这种情况。”

 

在现在已经创造出的双曲世界中，使用者们除了四处走动以外，并没有太多可做的事。但是该团队正在计划在虚拟现实世界中创造双曲房屋以及街道，甚至建造一个非欧几里得版本的篮球。

 

 

在非欧空间中做体育运动并非一个新生事物，先前已经有一位伊利诺伊大学芝加哥分校的拓扑学家David Dumas在学生的帮助下制造了一个虚拟现实(VR) 壁球游戏。在此游戏中，在撞向不同的方向后球可以返回起始点。

Dumas说：“解决如何使用虚拟现实(VR) 作为一种研究工具现在才刚刚起步。”运用数学原理的可视化一直帮助良多，比如使用分形的视觉实现使人更好地理解潜在的数学世界。

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：Rebecca Hills-Duty。 

译文作者：Jessie仪，哆嗒数学网翻译组成员，就读于布里斯托大学。

 

原文作者：Atheeta Ching，伦敦大学学院数理生态学博士。 

译文作者：radium，哆嗒数学网翻译组成员。

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

编者按： 有一个故事，说下雨天，大家都拼命的在雨中跑。有一个人却慢慢的走，别人问他为何不跑，他说，你没看见前面也在下雨吗，跑有用吗？很多人都是把这人当笑话来看的，但是这篇文章告诉你，问题没那么简单！

 

 

很多事情都影响着我们的生活，其中一件事便是天气，特别是下雨天未带伞（或者我们懒于将伞从包里拿出来）时的窘迫。凭直觉就知道似乎奔跑就是最好的选择，或者至少我们走快一点，就可以少淋一些雨。但是这也意味着雨点会以更快的频率从正面打在我们身上。

 
所以，如何才能让雨点在我们衣服上画的地图的面积少一点呢？这个问题实际上在过去的几十年里被众多的专家或爱好者们讨论过，无论是数学杂志还是像《流言终结者》这样的科普电视节目（事实上他们关于这个问题做了两期节目，第二期是对它的更正）。

 

让我们从最简单的模型开始，想象雨点匀速竖直落下。在图中，你就是那个灰色的长方形（因为下雨让你的心情不好，灰色可以表达这点心情）。

 

 

同时我们也要假设雨点均匀降落，其次第二个假设是假设雨点只从人的头上落下，而不考虑打在身上的情况。在这种情况下，无论雨点下落的速度有多快，你最好的选择便是“跑”。跑的越快你在雨中所淋到的雨越少。
 

好了，现在我们考虑，如果雨点因为风的缘故以一个角度降落在你身上又会如何呢？对于这个问题我们将会介绍一些真正的数学。和前面一样，我们将假设雨速度为定值Vr均匀下落。

 

雨域是这个问题的一个很重要的概念。这个区域包含了所有将会淋到你身上的雨点的初始位置。假设你以s的速度运动，因此在二维图上你的速度可以表示为向量Vu=(s,0)，这使得你在雨中花费的时间为1/s。

 

在你身上取一个点P，在雨域取一点Q，在t时刻后在这一点上的雨点会淋到你身上。然后我们就可以得出出雨点会在Q + Vr·t这一点上淋在你身上。而你的原始位置P可以表示成为 P=Q + Vr·t − Vt·t。从而对于每一个你暴露在外可以淋到雨的位置P,对任意时间t∈[0,1/s]，点P+(Vr−Vt)·t在雨域内. 

 

 

完整的下雨的区域由这些斜线勾勒出来了。每一条斜线的长度为 ||Vr−Vt||/s。这样就十分清晰了：如果雨以一定的角度下落，你应该跑的越快越好，缩短雨域的水平长度（下雨区域内的“宽”是定值，而和人的身高成比例）。

 

要是雨从你背后方来，又会怎样呢？这样一来，事情变得有一点复杂。雨点速度的分解为Vr=(V1,V2)，因为雨点有向前方的速度，因此 V1>0。于是一些不同事情将会发生（假设雨以一定的速度均匀下落）。之前我们提到，你以速度s移动。如果s>V1你就不会被你背后的雨淋到，但是你的头部和你身体的正前方会被淋到。

 

如果 s=V1，也就是说，你的速度和雨在你前进方向的速度一样，那么仅仅只有你的头部会被淋到雨。最后，如果s<V1显然你的背部和头部会被淋到雨，但是你的身体的正面会保持干燥。令Af为你身体正面或背面的暴露在雨中的面积，而At为你头部暴露在雨中的面积。

 

在我们之前的二维案例中，这些只是表示你所代表的长方形的高度和宽度。雨点淋湿的这些部分的总量分别正比于Rf =|V1−s|·Af  以及 Rt=|V2|·At。
 

上述中在雨中的时间为1/s，被雨淋湿的函数为R，正比于：

R1(s) = [(V1 - s)·Af + |V2|·At]/s 若 s≤V1

R2(s) = [(s- V1)·Af + |V2|·At]/s 若 s>V1

 

其中比例的乘子是雨的密度。注意这个函数可以被应用到之前的例子。即雨点向后方下落，V1<0。我们发现我们总会有R=R2，因此让R最小化的方法便是尽可能地增加s。

 

雨点向前落下的例子中我们有V1>0. 让C = -V1·Af + |V2|·At 然后注意到R是连续的R1是一个关于s的减函数，而R2的变化依赖于C的正负。

如果C>0，R2也是关于s的减函数，要取R的最小值，那么s应该增加到最大值。

如果C=0，R2是一个常值。我们可以通过取任意的s≥V1来最小化R

 

如果 C<0，R2是一个关于s的增函数，那么我们仅仅只能通过让s=V1来最小化R。例如：你精确地于雨水平分量相同的速度奔跑。

 

C依赖于你的体格和在雨中的速度。如果雨向前方的速度很小，那么你最佳的选择任然是尽可能快的跑。但是，如果雨向前的速度很大，使得C<0，那么你最好精确地于雨水平分量相同的速度奔跑。同时也意味着雨点会打湿你的头部，但这些都是理论上讲的情况。

 

关于这个问题还有很多复杂的模型，考虑不同的形状（不是正方形的情况下）或者突然来阵一阵大风，都会影响最终的结论。最后，我们将以Matthew Wright（很遗憾不是之前Chalkdust的成员）写的五行打油诗来结束。

固执的青春

暴露在雨中的执拗

若雨从背后拥抱

我我便与雨同行

但若迎风而行

最华丽的步调

便是与雨赛跑

 

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

2011年3月11号日本发生9.0大地震发生，这次大地震震中位于日本的一个港口，它也让整个世界包括很多地震专家们感到震惊。它猛力地提醒着我们对断层以及它们突发的和灾难性的行为是多么的无知。如何找到断层清晰准确的几何描述并测绘出周围区域存在的拉紧形变区，这依然是一个悬而未决具有挑战性的问题。如果我们能克服这个挑战，我们就能进行地震活动的模拟仿真，进而更好的评估它对指定区域所带来的的风险。

 

 

我的合作者是约内斯库（他在巴黎大学），根据切向位错原理，我们已经开发出了一套行之有效的方法来定位和描述活跃的断层。这套方法是基于如下的假设：只有表面观察结果可以获取并且无牵引的情况可以应用于该表面。

我们也根据GPS的观察结果探索了探测慢滑移事件（比如无声地震或者地震成核阶段）的可能性。我们的研究依赖于对于已观察到的表面位移的渐进估计。这种估计在导出我们称之为矩重建方法的过程中被首次使用。之后它也用于寻找地表面移场必要的条件。这些条件就导致了以下两个参数的引入：活化因子和置信指标。根据表面观察结果，这两个参数可以用有效的方法计算出来。它们表明了一个标准変位场的产生是否是归因于活跃的断层。

结合最小二乘最小化和矩方法，我们之后发展了一个综合的断层轮廓重建技术。我们仔细研究者我们的重建工作是如何受到观测仪器敏感性和地表观测点坐标方格的步长的影响得。计算这样坐标方格最大的允许步长是为了应用于不同的断层深度和方向。最后我们得到了基于虚拟数据的数值重建法。

 

对于这种准静态断层滑动问题的正逆性的数学分析现在已经完备了。我们当前在应用这种理论来记录在太平洋海岸的墨西哥附近的大型区域测量的移位数据。这的确是一项很有挑战性的工作，因为我们不得不应对有噪声且有错误的数据，有时用那种花费极高的仪器一个月才解决几毫米的位移测量，这样只能得到极其稀疏的数据。在墨西哥沉没地区，一个可靠的活跃断层的重建只有通过各种数学模型的结合才能实现，这些数学模型要合理地反映压力，地壳移位以及待恢复参数的指定物理界限。幸亏有两个世纪的观察调查工作，地球物理学家们可以知道这些界限。

所以有没有那么一天地球物理学家能够预测地震事件呢？不幸的是，地震预测可能永远不会像天气预测那样靠谱。最多可能有一天我们能更好地评估一下一个地区在接下来100年内会发生地震的可能性。那就是说，知晓断层和给定区域应力剖面的精确几何形状可能会对于我们预测地震事件的强度和震波形式有所帮助。

 

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：RICHARD SANDOMIR，纽约时报记者。 

译文作者：mathyrl，哆嗒数学网翻译组成员。

校对：donkeycn

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

雷蒙德·斯穆里安(Raymond Smullyan)，他的快乐，敏捷的头脑使他成为一个音乐家，魔术师，数学家，最妙的是，他还是一个创作谜题的逻辑学家（哆嗒小编注：实际上他的头衔里还有哲学家和道教学家），2017年2月6日（星期一）在纽约州哈德逊市去世，享年97岁。

 

他的亲人黛博拉·斯穆里安（Deborah Smullyan）确认了他的死讯。

 

 

斯穆里安教授是一名正儿八经的数学家，他的出版物和博士学位证明了这一点。但他最伟大的遗产可能是他设计的极其烧脑的逻辑谜题，它们或呈现在许多书籍中，或者只是出现在休闲的谈话中。

 

 

有时他们是一次性的，有时他们被嵌入更长的叙述中来解释数学概念，例如布尔逻辑，就像2015年他在《乔治·B的魔法花园和其他逻辑谜题》（The Magic Garden of George B and Other Logic Puzzles）中所做的那样；或者回溯分析，1981年他在《阿拉伯骑士的象棋奥秘》（he Chess Mysteries of the Arabian Knights）中进行了探讨。

 

 

他也是一个有趣的人。斯穆里安教授有着长长的白头发和胡子，长得像《指环王》系列电影中伊恩·麦凯伦（Ian McKellen）饰演的法师甘道夫（Gandalf）。他身材瘦长，讨厌健身，酷爱牛排和鸡蛋。他研究东方宗教。他讲老套的笑话，对身边的人表演近距离魔术。直到90多岁他仍带着激情和才华弹钢琴。 （尽管他年轻时因肌腱炎而脱离音乐事业。）

 

 

他对他自己的哲学、谚语情有独钟，例如，“我为什么要担心死亡？这不可能在我活着的时候发生！“

 

 

纽约城市大学研究生中心（Graduate Center of the City University of New York）的数学、哲学与计算机科学退休教授梅尔文·费廷（Melvin Fitting）回忆了斯穆里安教授的风采，在20世纪60年代，斯穆里安教授在叶史瓦大学（Yeshiva University）是费廷的老师，而费廷当时正在攻读博士学位。

 

教授在一次采访中说道：“他会微笑着期待他将要展示的许多美丽的东西。”

 

 

几十年来，斯穆里安教授似乎不停地创作的谜题，从中看到数学之美，并将其视为传播数学福音的工具。在他1982年的书《‘女士还是老虎？’以及其他逻辑谜题》（The Lady or the Tiger? And Other Logic Puzzles）中，他写道，如果希腊数学家将其作为一本谜题书，欧几里德的《几何原本》将会获得更大的普及。

 

 

他写道：“问题：给定一个等腰三角形，对应的两个角是否必然相等？为什么相等或者为什么不相等？”

 

 

他的谜题几乎是他本身的一部分，他与后来成为的妻子布兰奇（Blanche de Grab）第一次约会的时候就提出了一个谜题。

 

 

他向她提出的命题，就像他所描述的那样，一定能得到她的吻。回想起这件事，他写道，这是一个“赢得一个吻的相当狡猾的方式，不是吗？”

 

哆嗒小编插播：这是一个在数学圈流传很广的美谈。斯穆里安第一次见到女神时，达成一个约定——斯穆里安说一句话，如果这句话是对的，女神要给斯穆里安一张女神的照片，如果是错的则不给照片。斯穆里安说的话是：“你既不会给我你的照片，也不会亲我一下”。于是斯穆里安成功的获得女神的一个吻。

 

 

詹姆斯·麦迪逊大学（James Madison University）的数学教授杰森·罗森豪斯（Jason Rosenhouse），他在2015年编辑了一本书，书中赞美斯穆里安先生，对于那些以前不了解数学的人，他的谜题可以清晰地揭示数学之美。

 

 

“就像哄小孩子吃蔬菜，” 罗森豪斯教授在接受电话采访时补充说：“雷蒙德用一串逻辑谜题作为工具来展现诸如哥德尔不完备定理。“

 

 

马丁·加德纳（Martin Gardner），一位著名的数学谜题作者，把斯穆里安教授与牛津大学逻辑学家查尔斯·道奇森（Charles Dodgson）相提并论，道奇森也是以笔名路易斯·卡罗（Lewis Carroll）而更广为人知的作家。斯穆里安教授在1982年的书《爱丽丝漫游谜题王国：一个给八十岁以下儿童的卡罗式的故事》（Alice in Puzzle-Land: A Carrollian Tale for Children Under Eighty）中向卡罗致敬。

 

 

在其中一章，斯穆里安教授写道：爱丽丝心中思忖这个蛋人（Humpty Dumpty）是多么的混乱，但又相当合乎逻辑。

 

 

“我想知道，”她说，“他怎么做到既混乱又合乎逻辑的？”

 

 

在斯穆里安先生曲折的人生道路上，似乎有过一些令人困惑的逻辑。

 

 

雷蒙德·梅里尔·斯穆里安于1919年5月25日在皇后区法洛克威（Far Rockaway，Queens）出生，他的父亲伊西多尔（Isidore）是一名商人；他的母亲露西娜·弗里曼（Rosina Freeman）是一位家庭主妇。

 

 

他的求学经历是到处游学和不拘一格的。他曾就读于俄勒冈州的太平洋大学（Pacific University）和里德学院（Reed College），然后自己研究数学和逻辑。他还学习魔术。他创作了一些国际象棋谜题，这些谜题更为关注已经走出的棋步而不是将要走的棋步。

 

 

他以艺名Five-Ace Merrill在夜总会表演魔术，比如芝加哥Pump Room夜总会，他在那里工作获取报酬。他继续攻读并取得芝加哥大学的数学学士学位和普林斯顿大学的博士学位。他分别在普林斯顿大学、叶史瓦大学、纽约市立大学莱曼学院和印第安纳大学任教。

 

 

他的教学理念有点令人困惑。“我的原则是教给学生尽可能多的东西，并尽可能少地要求他们”，他对2008年的《Mathematical People: Profiles and Interviews》一书的作者Donald Albers和Gerald Alexanderson如是说。

 

 

但是，他补充说，明显的宽容所造成的影响是许多学生在他的课程中比在任何其他课程更努力。

 

 

斯穆里安教授身后遗下了继子杰克·科蒂克（Jack Kotik）、六位继孙子女和16位继曾孙子女。他的妻子布兰奇，比利时出生的钢琴家和音乐教育家，2006年去世。他的第一次婚姻以离婚结束。

 

 

科蒂克先生回忆说，他和妻子在纽约Elka Park的斯穆里安的房子里，听了有关职业运动员高薪的广播报道。他的母亲布兰奇说，他们的薪水过多了。

 

 

斯穆里安教授说，拿这么高薪水是不公平的。

 

 

 

“我说，‘雷蒙德，你比大多数人更聪明，不是吗？’”科蒂克先生在接受电话采访时说。 “‘是的，’他说。所以我说，'我认为这是不公平的。我们应该把你的大脑分出一部分分发给可以使用它的人。’”

 

 

 

“他沉默了一分钟，最后他说，‘我无法给出任何理由，但我不会这样做。’”

 

 

谜题是斯穆里安先生的一个重要组成部分 —— 逻辑学家打招呼和考验他人的方式。

 

 

当他遇到他最近的编辑罗歇尔·克伦泽克（Rochelle Kronzek）时，他要求她解答一些问题。

 

 

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

新浪微博：http://weibo.com/duodaa

“一开始吓到我了，但我想出了创造性的答案，”世界科学出版社执行编辑克伦泽克女士在接受采访时说，“他不止一次地笑了，因为他喜欢我的思考方式。看到别人如何思考，他从中得到很大的乐趣。”