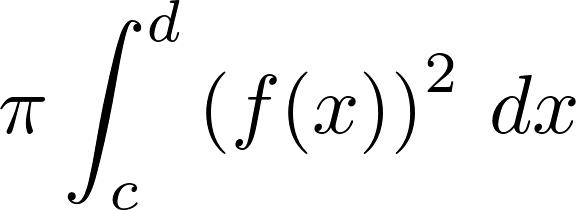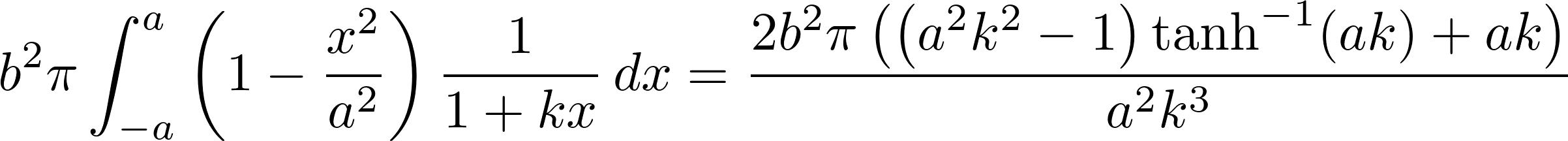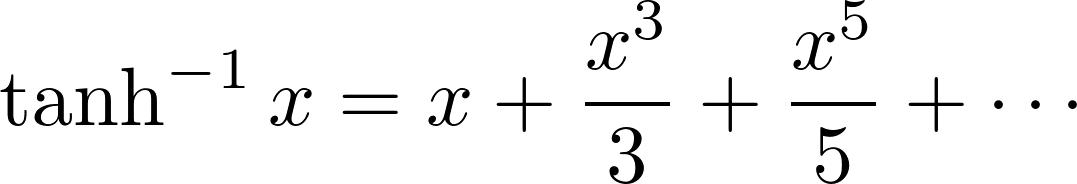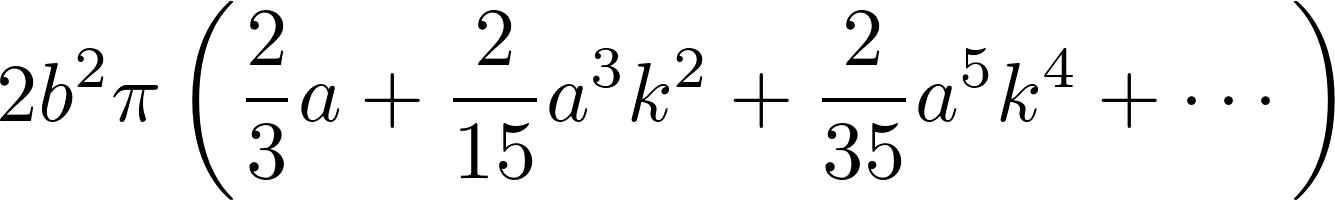关注 哆嗒数学网 每天获得更多数学趣文

本文原载于2019年2月27日《环球时报》上，原文标题《奥数不能功利也不能不给力》。由于篇幅受限，《环球时报》上刊出的内容有所删改，现将全文完整版发出。

第11届罗马尼亚数学大师赛（RMM）于25日于闭幕。美国代表队获得三块金牌，俄罗斯代表队获得两块金牌。而参加本次比赛的六位中国选手中最好成绩为15名，并获得了银牌。而中国队的团体成绩为第六位。

罗马尼亚数学大师赛被认为是中学生数学奥林匹克竞赛中难度最高的一项赛事，也是我国以国家队名义组队参赛的 3 项中学生数学国际赛事（IMO、RMO、RMM）之一。我国自第二届开始组队参加，由每年数学冬令营（CMO ) 中团体第一、第二的省份组队参赛，今年由上海组织队员参赛。

而据笔者了解，这次美国在RMM中派出的是二队上游选手，其他国家派出的选手大多是一线选手。中国本次是由上海的学习组织参赛。相当于中国队用省队于别人的国家队比拼，自然有些劣势。而且中国历年参加RMM的成绩都不是很突出。2016年的成绩更差，仅有1枚银牌，排名12位。

这算是的小众比赛，本来只有圈内的人关注。而且还有更差的2106年垫底，2016年也没这样引起如此大的关注。怎么会有这么热烈的讨论呢？笔者认为，之所以此次RMM的成绩在国内引起很大关注，很长程度上也是因为中国代表队已经连续4年没有拿到号称“数学世界杯”的国际中学生数学奥林匹克竞赛（IMO）冠军，自1985年首次参赛以来，中国从未经历如此长时间的冠军空窗期。再加上这四年当中，有三年的IMO冠军由美国获得，此次RMM又是美国压过了中国。在近来中美科技竞争的大背景下，这自然刺激了国人的神经。

过去30年，中国之所以能够在奥数竞赛上披荆斩棘、所向披靡，一个很大的秘诀是采用国家集训队这种方式，依靠一套完善的选拔体制选出数学技能较好的学生集训，提前准备比赛，让学生在比赛中能够有较好发挥。和很多人认知不同的是，美国在2000年之后也是IMO的传统强队，在比赛中经常能进前三，但始终无法撼动中国的霸主地位，所以普通大众没有关注他们。后来，他们吸取了中国的经验，强化集训队，聘请中国教练去辅导，甚至吸引国内比较优秀的学生去美国上高中。2015年，美国在IMO上刷新20多年未得总分第一的空白，外界当时以为是偶然，这几年来看，美国的实力的确已经整体变强了。

客观地说，只要IMO成绩没有掉出前三，中国队依然是奥数强队。个别奥数竞赛不能得到冠军，天也塌不下来。但笔者真正担心的是某些人对奥数学习赶尽杀绝的林林总总的手段，可能误导社会大众，导致包括数学在内的基础学科人才培养热度的降低。

奥数对教育的负面影响，各方面的论述不少。在曾经的加分与保送的诱惑下，很多学生学奥数可能不是因为真正对数学感兴趣，而是把奥数当做名校敲门砖，不少曾在奥数比赛上取得好成绩的学生，后来并没有走上学术路，而是走上了华尔街，让学奥数丧失了其初衷。

一种观点认为，奥数与一个国家的数学水平没有必然联系。而据笔者观察，以数学界的最高奖四年一届菲尔兹奖为例，近20年几乎每届都有一两位获奖者有IMO获奖经历，呈现正相关关系。很多对数学感兴趣的人，会以奥数为试金石，选择数学作为自己的终身职业。2006年菲尔兹奖得主陶哲轩就在公开场合表示对IMO的支持，他认为IMO的竞赛一方面给了青少年切磋数学的机会，另一方面也能促进交流。

现在国内的奥数成绩之所以没有没有体现在菲尔兹奖上，很大程度与中国数学整体底子较薄有关，毕竟诺贝尔的自然科学科方面的奖我们也才得了一个。这些都说明在基础学科方面，之前我们差的很远，现在仍然在追赶。然而，要成为数学或者科学强国，我们还需要积累，依然在路上。

一个好的现象是，从最近几年的趋势看，已经有越来越多奥数高手留在数学界。比如，奥数届内的巨星级人物“韦神”韦东奕、“恽神”恽之玮等。就是说，这些人会以学术上的成就为自己的毕生追求，这是中国社会整体向前发展的结果。

数学是自然科学之母，数学的发展与培养不仅在学科内部影响巨大，任何一项科技的运用和实践都与数学有关。现在，但凡时髦点科技词汇，诸如人工智能、大数据、5G通讯、无人驾驶……，背后都有一套高深的数学支持其运转。

国家建设初期，整体国力较弱，大学和社会中需要的是能马上转化并应用的成果，基础学科没有应用学科受到的重视大，这可以理解。而到了当下这个阶段，当所有可以引进和转化的资源慢慢转化殆尽的时候，薄弱的基础科学就可能成为创新的瓶颈。中国要发展，就必须培养一批甘坐基础科学冷板凳的人，而奥数就应当成为培养孩子对基础科学兴趣的阵地。

对“减负”和奥数的关系，社会上以往有很多讨论，但并没有讨论出一个很好的结果。而我们应该看到的是：首先，奥数之所以在过去呈现出一些功利性，是因为很多家庭有通过某种竞争关系实现阶层流动的需求，而普通学习和竞赛等途径对他们来说性价比最高。的确随着社会分层的加剧，形成了有钱人接受辅导班培训，没钱人学不到就吃亏的现实，甚至一些“天价辅导班”的出现影响了这种教育公平，但奥数本身不应背这种“破坏公平”的“黑锅”，也背不起。

另外，网上有人拿着个别题目抨击奥数摧残下一代。但这些题目很多都不是奥数题目，甚至根本不是数学题目，而是脑筋急转弯题目。它们被一些不良商人或者水平低劣的老师编进了奥数教材，这个“锅”也不应该奥数来背。相反，我们更应该普及数学，提高大众数学素养来帮助大众以及部分教师识别这种“伪奥数”。而奥数中有很多有趣味的问题，执行这种功能反而非常合适。

我们再来看，实际上取消了奥数加分以后，很多学生依然在学奥数，奥数的热度并没有实质上降低多少。这是因为奥数中的确有很多实实在在的数学技能，能够学到很多在课堂中学不到的东西。这些技能就会反映在学校学习当中。实际上高考中难度高一点的题目，或者高校自主招生中的题目，就有奥数的影子。况且学校也不傻，奥数比较好的学生，学习能力一般也比较突出，这也是学校愿意选择奥数好的学生的原因。所以，只要人类社会对数学的需求在，只要选拔制度在，对奥数之类的课堂外的数学学习需求就永远在。

以往学奥数有很强功利性，这种功利性应该被挤掉。我们应该考虑的是如调整、改良奥数，让奥数健康发展。但调整和改良并不意味着，从“全民奥数”那个极端，走向全民把奥数当“洪水猛兽”这个极端。

国际顶尖的奥数比赛一来是国际交流活动，二来也是顶尖人才切磋试金的机会，是选拔培养优秀人才的途径。现在有些地方将传统奥数竞赛叫停或整改。过去从小学直到高中的一整套比赛体制慢慢被瓦解，只保留几个最核心的赛事。这样“一刀切”，对数学人才的培养并不是好事。

关注 哆嗒数学网 每天获得更多数学趣文

关注 哆嗒数学网 每天获得更多数学趣文

昨天晚上，我们哆嗒小编发了一条消息，内容如下：

刚刚的2019年罗马尼亚大师赛(RMM)惨败，该赛事被称为中学生数学奥林匹克竞赛中难度最高的一项赛事，也是我国以国家队名义组队参赛的 3 项中学生数学国际赛事IMO、RMO、RMM之一。这一次中国居然下滑到第六，一块金牌都没有得到！美国队五个人当中有三枚金牌，差距已经明显拉开！

应该说，这条微博的措辞还是可能欠妥的，这里澄清一下。

第一，单论成绩本身，说惨败和下滑有点过于严厉。因为这不是中国代表对参加此项赛事的最差成绩。2016年，中国代表队参加此项赛事，同样没有金牌，最好成绩仅一枚银牌，团体成绩第12名。这回中国队4枚银牌，总成绩第6，不算最差。

第二，有人说中国派6人，美国5人，美国让一人，中国的总分依然落后。这个是不对的，RMM总分计算规则比较“奇怪”：首先参赛选手编号1-6，然后在编号1-5里取成绩最好的前三计入团体成绩。这回，中国对前三名都是35分，但是有一位选手的编号是6所以不计入总成绩，而把第四好的31分计入，总分101分。美国队总分117分。

第三，还是有人认为是惨败，原因是以往中国队都是派某个省队参加RMM，参赛选手水准参差不齐。这回虽然也是省队——上海队，但是上海一直是中国顶端奥数最强的地区之一，这回派的选手至少5个是国家队成员，堪称历次最强阵容，但成绩不理想。

但消息发出后，引发的讨论很有意思，大概分为几类：

1、 认为现在推行的快乐教育造成教育水平降低。
2、 认为是好事， 不能为几十个精英让几亿人陪着玩。
3、 认为学数学应该是兴趣，金牌不要太看重。
4、 认为无所谓，没见奥数好的工作后为国家贡献多少。

亲爱的哆嗒数学网的读者们，你们怎么看呢？

关注 哆嗒数学网 每天获得更多数学趣文

$p(x)=a_0+a_1x+\cdots+a_{m-1}x^{m-1}+x^m$

$q(x)=b_0+b_1x+\cdots+b_{m-1}x^{m-1}+x^n$

其中每个$a_i,b_i$是有理数，$a,b$分别是$p(x),q(x)$的根。

如何证明$a+b,ab,a-b,b/a$(分母始终不为零)是某个有理系数多项式方程的根？

就$a+b,ab$比较麻烦。

提纲:

1、 抽象代数证明

因为 $Q(a,b)$是有限扩张，所以是代数扩张，所以$a+b,ab$都在这个扩域内，所以是代数数。

缺点：对大部分人来讲，抽象代数的概念过于高端。而且是存在性证明。没法指出$a+b,ab$是哪个方程的根。

2、 一般高等代数数的初等证明

设$\alpha_1,\alpha_2\cdots,\alpha_m$和$\beta_1,\beta_2\cdots,\beta_n$是分别是$p(t),q(t)$全部根。

于是$r(x) = \prod\limits_{i}^m\prod\limits_{j}^n(x-\alpha_i-\beta_j)$。 ，所以$r(x)$展开后每个$x^k$次方的系数也是对称多项式。把这些对称多项式用$\alpha_i$,$\beta_j$初等对称多项式表示，得到系数是有理数。而$a+b$为$r(x)$中的一个根。

$ab$把$-\alpha_i-\beta_j$换成$\alpha_i\beta_j$同理。

缺点：过于暴力。如果要找具体的方程，过程似乎不太优雅。

方法3 推荐的优雅做法。

设$A,B$的特征多项式相应为$p(t),q(t)$。比如用相伴矩阵

$A = \left(\begin{matrix}0&0&\dots &0&-a_{0}\\1&0&\dots&0&-a_{1}\\0&1&\dots &0&-a_{2}\\\vdots &\vdots &\ddots &\vdots &\vdots \\0&0&\dots &1&-a_{{n-1}}\end{matrix}\right)$

定义运算$\otimes$,对于矩阵$C=(c_{ij})_{m\times n}$,$D=(d_{ij})_{p\times q}$

$C\otimes D = \left(\begin{matrix}c_{11}D&c_{12}D&\dots &c_{1n}D\\c_{21}D&c_{22}D&\dots&c_{2n}D\\\vdots &\vdots &\ddots  &\vdots \\c_{n1}D&c_{n2}D&\dots &c_{nn}D&\end{matrix}\right)$

就是把矩阵按$C$中数字倍数放大$D$然后拍成一个更大的$mp\times nq$矩阵。这实际上是张量积，可以不强调这一点，看成一个矩阵拼图游戏。

那么可以证明$A\otimes B$的特征值有$ab$，$I_m\otimes A + B\otimes I_n$的特征值有$a+b$

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，Math001，哆嗒数学网翻译组成员。

校对，donkeycn。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

菲利普·吉布斯并不是一位专业的数学家。因此每当他希望深入探究一个问题时，他便会去找那些即便是一个业余的数学家也能有所作为的题目。他的发现非常具有挑战性，甚至可以让那些思维最严谨的人为之疯狂。吉布斯在今年年初完成的一篇论文里，对一个将面积的测量精确到原子尺度的百年难题取得了重大突破。

法国数学家亨利·勒贝格在1914年寄给好友朱利叶斯帕尔的信中首次提出这一问题。信中提到：能够完全覆盖大量其他形状（它们的直径都是1个单位长度）且面积最小的图形是什么？

在那以后的一个世纪里，勒贝格的“万有覆盖”问题便诱发出一波思潮：自从它被提出后，对于这个问题的探究呈现出令人惊讶的进步。吉布斯的改善相比之下更为可观，尽管我们仍需仔细研究才能发现。

想象一下：在你的地板上放上一打大小形状各不相同的剪纸，现在你被要求设计出另一个大小刚好，并且能够完全覆盖那些剪纸的一个形状。通过叠加和旋转这些形状，你完全可以凭感觉找到你的解决方法。但是当你找到了这个“通用”的覆盖，你如何知道他就是最小的那个呢？你可以想象出：一整天都面对着你构造出的形状，在这里或那里发现一点可以修剪的地方。

这就是勒贝格“万有覆盖空间”问题的灵魂所在，它所考虑是其内部任何两点相距都不会超过一个单位长度的形状。单位圆是最明显符合这一条件的；当然也有许多其他符合条件的形状，对于初学者来说，可以举出：等边三角形、正五边形、正六边形以及由三段弧所组成的曲边三角形（勒洛三角形）等例子。这种形状的多样性使得我们很难找到它们的最小覆盖空间。

收到勒贝格的来信后不久，帕尔意识到正六边形是一个万有覆盖（边长为1/sqrt(3)，其中sqrt表示开根号）。之后他又做了一些改进，他发现当他从六边形上切下两个不连续的角所得到的形状面积更小，但仍是一个万有覆盖。

“取一个新的六边形，把它放在原来的六边形上面，将新的六边形旋转30°，这样你就能切下两个角；这就是帕尔的方案。”吉布斯说道。

在接下来的80年里，另外两位数学家在帕尔的万有覆盖上做了进一步改进：1936年罗兰·斯普拉格去掉了某个角附近的一部分；1992年汉森从右下角和左下角去掉了两个小的微乎其微的部分。汉森的面积节约方案示意图可以让我们知道它节约了哪部分，但是这难免会让我们对其节省的面积大小产生误会：他所截去的部分是0.00000000004单位面积大小。

.
“你不可能真的把这些碎片画出来，因为他们都是原子大小的。”约翰·贝兹，一位来自加州大学河滨分校的数学家这样说道。

2013年，贝兹在他颇受欢迎的数学博客上写了一篇关于勒贝格万有覆盖问题的文章，并在文中把这个晦涩难懂的问题表述地使人通俗易懂。他承认自己被这个问题所深深吸引，就像人们饶有兴趣地看着昆虫在水里扑腾一样。

“我对这个问题的兴趣甚至有些病态，”贝兹写到。“我不知道这个问题为何重要，我也看不出它与其他那些美妙的数学有任何联系。只是，可能和你一开始所想的相比，它似乎难得令人惊讶。我很佩服探究这一问题的人，就像我很钦佩那些决定滑雪横穿南极洲的人。”

菲利普·吉布斯从没滑雪穿越南极洲，但他读过贝兹的博客。当他看到勒贝格万有覆盖问题的帖子时，他想：“那正是我苦苦搜寻的东西。”

原子剪刀

小时候吉布斯就梦想着成为一名科学家。他在剑桥大学获得数学学士学位，并在格拉斯哥大学荣获理论物理学博士学位。然而在此后不久他便失去了学术研究的热情，转而成为了一名软件工程师。他曾从事船舶设计系统、飞机控制系统以及金融系统等，直到2006年退休。

吉布斯仍保留着对学术问题的兴趣，但作为一名非专业研究人员，他能做的屈指可数。“作为一名独立科研人员，我很难跟上当今科学发展的进度，”他说道。“但如果你找到了合适的问题，那么你就可以进行一些探究，并得出一些有用的结论。”

勒贝格的万有覆盖问题正是这样的问题，它从未引起数学家的太多关注，所以吉布斯觉得他可以在这个问题上有所作为。他也意识到可以运用自己的编程基础来增加自己的优势。“我经常寻找那些可以运用计算机来进行数学实验的问题，”他这样说道。

2004年，吉布斯对200个随机生成的直径为1的形状进行了计算机模拟，模拟的结果表明了他也许能在之前的最小覆盖面基础上再去掉顶角附近的一些区域。随后他将这个想法展开，并证明了新的覆盖对所有可能的直径为一的形状都适用。吉布斯把他的证明寄给贝兹，后者则与他的一名本科生卡琳·巴格达萨恩一起帮助吉布斯将他的论证进一步修改成更正式的数学形式。

他们三人于2015年2月将他们的论文发表在网上。文中，他们把最小万有覆盖面从0.8441377减少到0.8441153单位面积。尽管减少的部分只有0.0000224单位面积，但这却几乎是汉森在1992年减少的面积的100万倍！

吉布斯确信他可以做得更好。在十月份发布在网上的一篇论文中，他又从原有的覆盖面上剪掉了相对较大的一部分，从而把整体面积减小到0.84409359单位。

他的策略是将所有直径为1的形状移到他早些年发现的万有覆盖的某一角，然后把对角部分剩下的任何区域都去掉；然而从节省面积测量的角度来说，却是非常精确的。吉布斯所运用的技术都源于欧式几何，但为了让每个高中都能看懂，他需要确保每一步都十分精确。

“从数学角度来说，这只是高中几何难度，但是它几乎让人为之疯狂。”贝兹这样写到。

如今，吉布斯仍保有“发现最小万有覆盖”的殊荣，但是他的位置并不牢固，他相信任然有更小的万有覆盖以待我们发现。对贝兹来说，他则希望吉布斯所带来的对勒贝格这一问题的新关注能够激发其他数学家的兴趣，从而进一步完善并丰富现代数学技术。

“解决这个问题可能会涉及到非常不同的想法，”贝兹说道。“尽管我不知道这些想法具体是哪些。”

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

最近某演员的“学历门”事件火了。这位演员晒出其博士后录用函后，广大硕士、博士网友门没有查到该演员的相关论文。于是，所有人都开始质疑其学历的含金量以及获得学位的程序是否公正的问题。

平心而论，这位演员在各个影视作品的表现还算小有所成，有没有这个博士学位根本不会影响他在娱乐圈内的发展。自己发个博士学历的微博无非就是吹吹牛X，得瑟得瑟，满足一下自己被捧为学霸的快感而已——这种事情很多人做过吧。但他忘了，这些做学术的博士们其实是非常较真儿的人，他们用学术上的严谨态度和求证方法把这位演员搞得狼狈不堪。

其实，娱乐圈内用“学习好”标榜一些东西是屡见不鲜的。其中，因为数学学科难度大，学科知名度高，所以用数学来装X获得的更多的“膜拜式”关注，于是不少艺人、节目就利用数学来装X了。但俗话说，没有金刚钻，不揽瓷器活。这些利用数学装X的活动，也有玩脱靶的时候——装X未成，吐槽遍地。

以下便是哆嗒数学网小编为你整理的五个著名的数学装X失败事件！

No.5 《奔跑吧，兄弟》：关晓彤因会解二元一次方程被封学霸。

《奔跑吧，兄弟》是一款竞技真人秀节目。参加节目的明星们会被要求解出一些谜题通关。其中有不少是数学题。第一季，因为“0”是不是自然数的问题，而引发讨论。不过情有可原，因为只是不同时期的规定而已。

而第六季，因为关晓彤解出一道简单二元一次方程，而被其他人用膜拜的眼光看着，字幕还不断暗示关晓彤的数学有多好，第二天“学霸关晓彤”还上了热搜。这个的吐槽显然超过了上一个……

哆嗒君点评：这个事情关晓彤本人也许有点无辜，毕竟这个“学霸”不是她自己封的。就公开的资料显示，关晓彤的数学高考能上130+，应该说能到这个分数的人，数学水平已经超过绝大多数普通人了。槽点在于，因为解出每个初中生都会的题目，就被其他人捧为学霸，——本来是想秀某人有多好，却变成了秀其他一大票人是有多缺智……

No.4 电影《少年班》：用占卜算卦解出数学题目。

《少年班》是一部青春片。这部由孙红雷、周冬雨参演的电影在豆瓣的评分在5+左右，应该说是一个不好评分。

电影中有个剧情是，主角们需要现场在黑板上解出一道题目，才能有资格参加一项国际大学生的数学竞赛。而所有主角都在题目卡住了，参加竞赛的前景突然暗淡了下来。仔细辨认题目，题目差不多是要证明卡莱曼不等式，的确是有竞赛考过，这个X装的不错。

但是，解决这个问题的过程是：其中一位主角拿出他的“文王金钱卜”，在教室里算了一卦，根据卦中指示解出了题目，少年班的主角们瞬间翻盘！

哆嗒君点评：可以理解编导组设置这个剧情的初衷。一些高智商人总有一些让人无法理解觉得神奇的行为方式。但无论科学还是数学世界里，这种迷信的神神叨叨的东西干扰工作是最被人反感的——最后没人觉得这个人神奇，剧情过于无厘头。

No.3 《非诚勿扰》：证明了哥德巴赫猜想

《非诚勿扰》是国内最著名的相亲节目了，节目引发的大讨论不少。

有一期，有一位36岁的男嘉宾自称从七岁开始迷恋数学，自认为是一个数学奇才，并且声称证明了哥德巴赫猜想。而自己最大的愿望是当一名数学老师，这样能把数学的优雅和美丽传播给下一代。节目组说无法判断男嘉宾证明的对错，呼吁专业人士或机构帮助其核验。

哆嗒君点评：失败点主要在于如果经常了解数学新闻，这为男嘉宾的路数是典型“民科”路数，却没有人指出——之前没有论文成果，一上来就说解决大问题。在现场还没人挑明这一点，反而在讨论“兴趣能不能成为工作”的问题。难以想象，如果这位男嘉宾成为数学老师，将传播什么样的数学给下一代。

No.2 电视剧《历史转折中的邓小平》：穿越的数学教材

《历史转折中的邓小平》是一部主旋律电视剧，讲述邓小平1976年至1984年的事迹。电视剧的第九集是讲教材改革的，里面出现的小Bug让人忍俊不禁。

剧情是说当时中国教材严重落后，需要重新编写。这时，需要从国外采购一批外国教材做参考。于是，就出现了下面的场景——主角拿着一本英国作者马修斯的《向量微积分》，感慨外国教育的先进。——等等，这本由斯普林格出版社的教材是其“斯普林格大学本科数学系列”中的一本，是怎么也是2000年左右出版的，难道穿越了？

这还不是最过分的，后面还有一个剧情。剧中一角色拿着黄澄澄的GTM的数学书（仔细辨认，可以辨认出是GTM73，《代数》(Algebra)），硬要说这本书是英国高中生物教材。

哆嗒君点评：把历史剧拍成穿越剧就罢了，可以忍。你把研究生的数学的GTM教材硬说成高中生的生物教材，你让那些还在数学专业里摸爬滚打的同学们情何以堪？

No.1 靳东：看了一些诺贝尔 数学奖得主写的小文章

应该说靳东还是有很多成功的影视作品。2017年，红的发烫电视剧《我的前半生》的主角贺涵的扮演者正是靳东。如果好好拍戏，在演艺圈内也是一位非常优秀的演员。

但是，靳东总喜欢标榜他有多喜欢读书，而且是读有文化、有内涵、有难度的书。在一次接受采访的时候，靳东如是说道：“因为要扮演外科教授，所以要了解很多比如肋骨和切口的位置，神经系统如何工作之类的学术问题，而牵涉的数学知识就会去翻阅‘诺贝尔数学奖’得主的小文章。”

这下，好玩了。无论你是了解诺贝尔奖，还是了解数学的各大奖项，都应该知道——诺贝尔奖里没有设置数学奖。数学的最高奖项也应该是菲尔兹奖、阿贝尔奖、沃尔夫奖之类。靳东的这一番发言，引发各路知识圈内的网友吐槽。于是有媒体评价到，靳东的“精英人设”就此崩塌。

哆嗒君点评：就用某网友的一句话——咱别装了行吗？

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者：John D Cook。

翻译作者，独行者，哆嗒数学网翻译组成员。

校对，333。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

之前的一篇文章，我们已经知道如何用方程来拟合鸡蛋的形状。在平面上，我们有下列公式(1)

这篇文章的主要内容是为了求出鸡蛋的体积。通过将函数绕x轴旋转，我们可以由此求出体积。并且，我们还会把它和椭球的体积进行比较。

首先，将函数f(x)在区间[c, d]上的图像绕x轴旋转一周，于是我们便得到体积公式(2)

即使被积函数是关于函数f的平方，我们也能轻松地用积分求出来。因为在这个例子当中，如果我们将曲线的方程显式地表示为y关于x的函数时，函数表达式中会有开平方，从而消去了式子的中的平方运算符。因此，我们的体积可以求得（3）

接下来，我们将鸡蛋的体积和椭球进行比较。为了更容易看出两者之间的差异，我们现在将式子中反双曲正切函数用幂级数展开（4）。

那么，体积的表达式便如下所示（5）

我们会注意到，如果a=b=r，k=0，那么式子便会简化成一个球。该球半径为r，体积为4πr³。如果a、b不一定相等，但是如果k=0，那么，便是椭球的体积4πab²/3。

定律一：k对体积影响甚微。在上述级数中，k只出现在2次及更高次的项中。这表明在一阶近似时，鸡蛋的体积（假定形状遵循我们所给的公式,注意到|k|很小）便约等于一个拥有相同长轴和短轴的椭球的体积。另外，我们也注意到k只出现在偶次幂的项中。这一点与我们之前的直观判断一致。在前文中，我们认为改变k的符号仅仅表示将鸡蛋翻个身，并不会改变鸡蛋的体积。

定律二：如果展开到2次项，鸡蛋的体积和椭球的体积之间相差了一个k的二次函数。为了将一个椭圆变成一个鸡蛋的形状，你需要将一端变得平整，而另一端则要变得更尖。但同时还要保持长度和宽度不变，那么你还再要增加体积。你要在平整的一端增加出来的体积会比尖的一端失去的要多一些。

之后的文章将会讲解如何求鸡蛋的表面积。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

1956年，中央新闻纪录电影制片厂推出了一部纪录电影《春节大联欢》，这个可是现在“春晚”的前身。各界著名人士：老舍、巴金、周立波、杜鹏程、孙谦、陈其通、袁雪芬、梅兰芳、侯宝林、钱学森、华罗庚、郭沫若、荣毅仁、乐松生、郭兰英、张瑞芳、白杨、赵丹等参加了大联欢。

那个时候不是直播，实际上《春节大联欢》是一部记录电影，是录播。按现在的眼光，录播的晚会都被”剧透“得一干二净，应该没什么看头了。但你要知道，在那个年代你就算找遍十条街都找不到一台电视机，更别说什么利用移动app、网络新闻获知信息了。没有电视机，大部分都是通过社区、工厂、村委会等组织的电影观看活动看到的这部《春节大联欢》。所谓看电影，也不是现在那样，2d、3d影院随便挑，美美拿着爆米花和可乐，享受着最好的视听设备带来的娱乐体验。——而是，组织者找个平坦的露天坝子扯一块大幕布，用最简陋的电影机器关注投影上幕布。观众自带小板凳，端上一盅茶水，提前到场。先来后到，自选位置。所以，有的地方，这种电影又叫”坝坝电影“。大部分人，都是过完年，在坝坝电影看这部春节大联欢的。

我们是数学网不是？当然关注数学家。在这部剪辑过的90秒的视频里。钱学森被介绍时，介绍的头衔还是大家熟知的”空气动力学家“，实际上，鲜为人知的是，钱学森有着数学博士的学位，还写过一本《工程控制论》，控制论一般认为是应用数学的分支之一，所以说钱学森是应用数学家也不为过。

在郭沫若出场时，隆重介绍了华罗庚。华罗庚那个时候其实已经46岁了，但是在影片里看着非常年轻帅气。和网上看到的那位白发苍苍的慈祥老人完全是两种感觉。也许，用帅气的形象宣传华先生，能为数学招揽更多的粉丝呢。

视频中，无论什么人出场，介绍的头衔都非常简单。郭沫若也就称呼一句”先生“，巴金的头衔就是一位”老作家“，钱学森介绍的时候，就说他是”1955年回祖国怀抱的专家“。现在一些搞营销的，还不知做了什么，就一堆宇宙级头衔蹦出来，这些介绍不知道比他们朴素了多少倍。

在网上能搜索到这个《春节大联欢》的完整版，时常1个多小时。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa