关注 哆嗒数学网 每天获得更多数学趣文

这段时间，有一堆数论男孩玩的很疯。他们在疯狂的把一堆整数拆成3个整数的立方和。

我们知道，9n±4型的整数是不可能写成3个整数立方和的。但是除了这些整数，其他的整数是否能写成三个整数的立方和还没有研究出一个理论上的统一结果。于是人们就开始一个一个的试，看看能不能找到什么规律。

今年，这样的问题突然在社交圈热闹了起来。

先是3月，有人第一次把33写成3个整数的立方和，33 = 8866128975287528³ + (-8778405442862239)³ + (-2736111468807040)³。使得人们在100以内的没有写成整数三立方和的仅有42了(9n±4型的整数除外)。

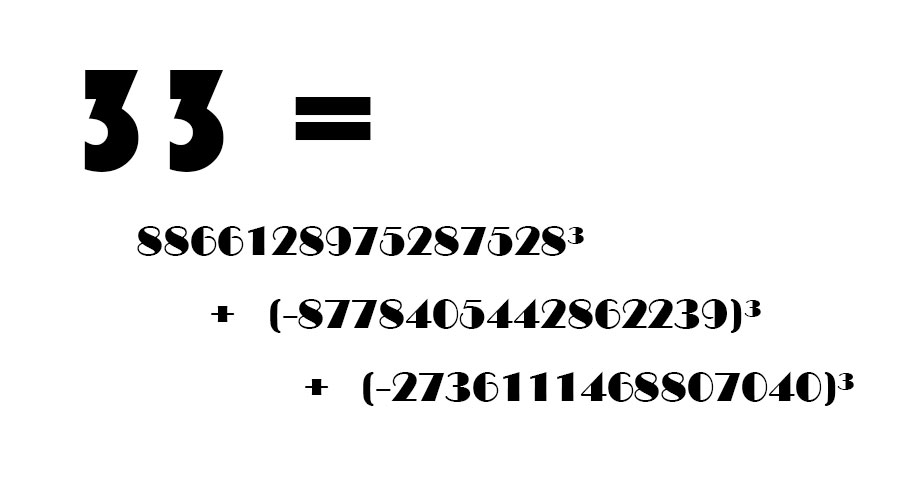
然后9月，100以内最后一个42也被解决了，于是100以内立方和全部收集完成。42 = (-80538738812075974)³ + 80435758145817515³ + 12602123297335631³

——于是有人说，这说明宇宙的终极奥义不是42。

于是，下个目标，就是收集1000以内的。实际上，1000以内的剩下没解决的并不多，9月初还剩下114, 165, 390, 579, 627, 633, 732, 906,921, 和975。几天前906解决：906 = (−74924259395610397)³ + 72054089679353378³ + 35961979615356503³ 。

为了收集可能的更多规律，很多人开始研究同一个数，不同写法之间的联系。对于同一个数，他的写法是唯一的、有限多种还是无限多种成为一些数学家的兴趣点。

1953年，数论大师，大名鼎鼎的莫德尔在他的论文《关于方程x²+y²+z²+2xyz=n的整数解》(ON THE INTEGER SOLUTIONS OF THE EQUATION x²+y²+z²+2xyz=n)中讨论了一个问题。他说他自己对x³+y³+z³=3这个方程了解甚少，除了知道1³ + 1³ + 1³ = 3和4³ + 4³ + (-5)³ =3这两组解。他提到他觉得那篇找到这个方程的第三组解都是非常困难的。

于是有人试图去找这个方程的第三组解。66年过去了，还真找到了。果然数字大的惊人：3 = 569936821221962380720³+(-569936821113563493509)³+(-472715493453327032)³ 。

找到的办法当然还是用椭圆曲线的相关知识缩小范围，再用集群网络计算机计算。这回算了7个多小时。著名数学普及节目Numberphile做了这个结果的一个专题。

之所以在朋友圈，这样的问题那么火，是因为难得有那种既有难度，大家又看的懂，还能玩的起来的问题。而且每个人都可以试试。甚至可以当成小学奥数题发给自己班里的数学学霸整蛊他们。

总之，能在朋友圈玩数学，还是比较高端的玩法。我们哆嗒数学网的小编至少认为比传播无脑鸡汤文好多了……

关注 哆嗒数学网 每天获得更多数学趣文

关注 哆嗒数学网 每天获得更多数学趣文

腾讯科技讯 9月20日消息，经过四个多月的评审，2019年“科学探索奖”获奖名单今日正式向社会公布。50位获奖人经过层层选拔，最终从千余名申报人中脱颖而出，每位获奖人将在未来5年获得由腾讯基金会资助的300万元人民币奖金。

“科学探索奖”设有数学物理奖，此次有5位学者获得此奖。来自北京大学的刘若川是这五位学者中，唯一一位以数学为主要研究方向的学者。

刘若川于1999年至2004年在北京大学数学科学学院学习，获学士、硕士学位，2008年获美国麻省理工学院博士学位，2012年回到北大，在北京国际数学研究中心任职。刘若川的主要研究领域是算术几何与代数数论，他在p进霍奇理论、p进自守形式与p进朗兰兹纲领等方向取得了一系列重要成果，特别是与人合作在几何相对p进霍奇理论方面做了奠基性的工作。

“科学探索奖”探索奖的发起人包括众多学科大牛，其中包括著名数学家张益唐。

按“科学探索奖”规定，该奖只授予45岁以下全职在中国大陆工作的学者。“科学探索奖”管理委员会表示，希望“科学探索奖”能成为青年科技工作者潜心探索未知世界的精神激励，吸引更多青年人投入到基础科学和前沿技术的研究之中。 腾讯基金会将长期运营“科学探索奖”，今后每年“科学探索奖”将评出50位获奖人。

有人认为，民间资本对基础学科加大投入是件好事。一方面，机制比传统体制灵活，资源配置更加有效率。另一方面，有利于这些高升学科在普通大众的普及。

据悉，2019年“科学探索奖”颁奖典礼将于11月2日在北京举行。

附全部获奖名单：

关注 哆嗒数学网 每天获得更多数学趣文

关注 哆嗒数学网 每天获得更多数学趣文

9月8日和9月10日，著名华人数学家，菲尔兹奖得主陶哲轩分别在ArXiv和其博客上发表他关于考兰兹猜想的一个结果(9月13日ArXiv上的论文有修改)，引发数学社交圈的讨论。

考兰兹猜想，俗称3x+1，说的是这样一个猜想：

对于一个初始的正整数，如果它是偶数我们就把它除以2，如果是奇数就把这个数乘以3再加上1。这样将得到一个新的数字，再把这个新得到的数做之前重复的操作——如果它是偶数我们就把它除以2，如果是奇数就把这个数乘以3再加上1，然后又继续得到一个数。这样的操作一直重复下去，我得到一串正整数的数列。3x+1说，无论最早的初始正整数是多少，这一串数列最终都会进入4,2,1,4,2,1,....这样的循环。

比如，我们用10作为初始正整数：

因为10是偶数，所以除以2，得到5。

因为5是奇数，所以乘以3加上1，得到16。

因为16是偶数，所以除以2，得到8。

因为8是偶数，所以除以2，得到4。

因为4是偶数，所以除以2，得到2。

因为2是偶数，所以除以2，得到1。

因为1是奇数，所以乘以3加上1，得到4。

因为4是偶数，所以除以2，得到2。

因为2是偶数，所以除以2，得到1。

……

我们可以把3x+1猜想的表述改变一下，设初始正整数是n，上述操作得到的数列中一定有个最小值S(n)。那么3x+1猜想就是说S(n)=1。

于是，很多数学家开始研究S(n)的性质，比如去寻找S(n)可能的上界f(n)，即S(n)≤f(n)。

1976年，Terras证明了,几乎对所有的正整数n(在自然密度意义下)，有S(n)<n。

1979年，Allouche证明了，对任意a>0.869，几乎对所有的正整数n(在自然密度意义下)，有S(n)<n^a(x^a表示x的a次方，下同)。

1994年，Korec证明了，对任意a>ln3/ln4≈0.7924，几乎对所有的正整数n(在自然密度意义下)，有S(n)<n^a。

这一次，陶哲轩发表的结果是对上述一些成果的改进，他试图证明，只要{f(n)}是一个趋于正无穷的实数列，那么几乎对所有的正整数n(在对数密度意义下).有S(n)<f(n)。

陶哲轩还特别指出，这个结论中的f(n)可以是增长非常慢的的数列，比如f(n) = lnlnlnln(n)。

陶哲轩的文章引起了社交圈的讨论，比如著名的网红橄榄球球员数学家Urschel转发了陶哲轩的博文，并感慨自己虽然同样是做数学的却做不到这种深度。

在众多讨论中，一位来自美国新泽西州立罗格斯大学数论教授Kontorovich唱起了“反调”。他的观点是，应该想办法去证明3x+1猜想是错的。

注意到，就算按这个思路把右边的f(n)改进成了f(n)=2也不能说3x+1被证明了。因为结论有“几乎”的表述，比如自然密度意义下，几乎所有的正整数都是合数，但谁都知道素数(质数)有无穷多个。陶哲轩自己也在博客评论区发言说，把“几乎所有”变成“所有”似乎还有巨大的鸿沟要跨越。

按Kontorovich的想法，这些“几乎”不存在的反例可能真正存在。并引用了自己之前的一些研究结论，以及Conway对3x+1猜想推广的一些结论来佐证自己的直觉。

Kontorovich说多年来他一直试图通过构造一些“奇怪”性质初始值来推翻3x+1猜想，未果。并呼吁包括博学者计划(PolyMath)在内的数学组织来一起找反例。英国数学家，同样是菲尔兹奖得主的高尔斯也参与了Kontorovich教授的讨论。

由于陶哲轩的论文题目和论文结论都多次用到“几乎”(almost)字样，于是网上出现了“陶哲轩几乎证明了考兰兹猜想”为标题的文章。高尔斯认为如果这样表述陶哲轩的结果，就是假新闻。

关注 哆嗒数学网 每天获得更多数学趣文

9月8日和9月10日，著名华人数学家，菲尔兹奖得主陶哲轩分别在ArXiv和其博客上发表他关于考兰兹猜想的一个结果(9月13日ArXiv上的论文有修改)，引发数学社交圈的讨论。

关注 哆嗒数学网 每天获得更多数学趣文

还记得2018年随着法国总统马克龙访华的这位怪叔叔吗？他穿着诡异，胸前总是扎着大大的领结，领口总是别着一个夸张的蜘蛛胸针。别人都轻装上阵，他去了哪里都背着满满的背包，感觉不是来做“国家级”的访问，倒向是来自由行旅游的。

这人是谁？说来，此人在数学界可大名鼎鼎！他的名字叫维拉尼，2010年菲尔兹奖得主。——大家知道诺贝尔奖没有设立数学奖，而菲尔兹奖在数学界有着“数学诺贝尔奖”的别称。菲尔兹奖只颁给40岁以下的数学家，而且还是四年颁发一次。从这个意义来讲，得菲尔兹奖比得到一年一度的诺贝尔奖的难度要大得多。

由于穿着时尚夸张，同时喜欢参加各自社会活动。维拉尼在数学界有着“数学界的Lady Gaga”的别称。在街上的回头率也极高，他那种复古打扮让不少人回头。

维拉尼在2017年当选议员后，正式从政，后来成为总统马克龙“前进运动”团队的一员随马克龙访华。很多人也许好奇，一两年过去了，这位数学怪咖现在在做什么？

答案是：维拉尼前不久宣布，他要竞选巴黎市市长！

不过这回马克龙对维拉尼的决定可能要郁闷一阵子了。因为马克龙个人希望自己的最亲密盟友，前政府发言人本杰明·格里沃代表自己的“前进运动”阵营参选法国首都的市长。

有民调显示维拉尼和格里沃的支持度相差无几，几乎是齐头并进。如果两人只有一人参选，那么将获有巨大优势。但如果两人都参加市长的角逐，那么这个优势将被分割。而如果真是两人同时参选，将对现任市长社会党人安娜·伊达尔戈寻求连任有利。

维拉尼说：“巴黎有很多复杂的问题需要解决，而这些问题我们可以一起通过发挥自身的优势来解决。”维拉尼说，“再从政之前我一直在和各种复杂的问题做斗争。”他最后还说，他将成为首位“真正的环保主义市长”。——现任市长就是因为交通拥堵和空气污染问题被巴黎市民诟病，而支持率降低。

“前进运动”的一些大佬认为，维拉尼的政治抱负注定要失败，甚至有人提醒：“作为数学家应该把这个算清楚：分裂意味着失败，团结就是胜利。”

不过，维拉尼团队正在非常谨慎的处理这些问题，尽量不让竞选行为变成对马克龙总统权威的挑战。“维拉尼已经告诉总统马克龙和总理菲利普，可能的选情更替并不是对他们的故意冒犯。”一位来自维拉尼身边的消息人士说。

值得一提的是，法国知名数学家从政似乎本身不算什么新鲜事。大家熟悉的法国大数学家拉格朗日、拉普拉斯就是拿破仑时代的官员。另外，著名数学家，因“潘维勒超越函数论”而闻名的数学教授保罗·潘勒韦甚至在第一次世界大战关键时刻和1925年金融危机时两次出任法国总理。

关注 哆嗒数学网 每天获得更多数学趣文

关注 哆嗒数学网 每天获得更多数学趣文

每个人都有自己的数学老师，在数学课堂上一定发生过不是让人啼笑皆非的囧事。今天教师节，和大家一起分享一下这些数学家讲课的囧事，开开心心的和老师们一起过节。

牛顿(Newton)最伟大的数学家、物理学家之一。他的贡献不再赘述。

当时在剑桥，牛顿讲课是出了名的烂，大家都听不懂他讲的东西。之所以听不懂还不全因为他课程的难度，而是因为他口齿不太清晰。

牛顿的课经常只有稀稀拉拉的一两个或者两三个人在下面听——有人觉得就算面对空空的讲堂，他也能将课授完。

林德曼(Lindemann)，就是证明了圆周率π是超越数的数学家。

林德曼的课堂上的大部分时间，台下的听众都听不清他说的什么，偶尔有时候听清了，也是一些艰深难懂的内容。

有一次林德曼上课，所有有人都听清且听懂了林德曼的话，还和台下的人产生了互动交流——所有人都告诉他：“老师，你讲错了！”

哥德尔(Gödel)，伟大的数学家、逻辑学家、哲学家。以"哥德尔不完备定理"闻名于世。

哥德尔长期在普林斯顿高等研究院工作。他性格孤僻，不喜欢与人交流，单偏偏和爱因斯坦关系不错。

一次，哥德尔被安排到普林斯顿高等研究院的法恩楼(Fine Hall)演讲。所有听众大家都记住了这次演讲——不是演讲内容，而是演讲风格。哥德尔居然全程面向黑板而背对观众——你没看错，是全程！

于是，所有人都记住了哥德尔的背影。

美国数学家莱夫谢茨(Lefschetz)是代数拓扑领域的大牛，据说他讲课非常跳跃，以至于几乎很难有人懂他在讲什么。

他讲课的风格大概是这样的：

“一个黎曼曲面一定是个豪斯多夫空间……”

“——你们都知道什么是豪斯多夫空间吧？……”

“——它也是紧的……”

“——我想，他还是一个流形……”

“——流形，嗯，你们都懂……”

“——所以我要讲的是一个复杂的定理——黎曼-洛赫定理。”

兰道(Landau)是数论和函数论方面的专家，他还讲过傅里叶分析相关的课。

兰道是德国人，讲英文的时候有严重的德式口音。有一次讲到吉布斯现象的时候，他声音洪亮的说：“这个现象是英国Jail的数学家Jibbs发现的。”

这时候，下面有人提醒兰道老师：

“第一，这位数学家是美国的而不是英国的。”

“第二，他叫Gibbs，而不是Jibbs。”

“第三——这一点一定要说清楚——他是在Yale(耶鲁)而不是Jail(监狱)。”

闵可夫斯基(Minkowski)是擅长数论、代数以及数学物理的顶级大神。

一次他上课，向学生们自负的宣称:“四色猜想之所以还没证明，是因为只有一些三流的数学家在做破解它的工作。下面我就来证明它！”于是闵可夫斯基拿起粉笔在黑板上奋笔疾书，但一直到下课都没证明出来。

于是他的课一直这样的状态，一连几周过去了……

一个一个阴霾的早上，闵可夫斯基走进教室，突然一道霹雳闪过，雷声隆隆。

闵可夫斯基严肃的说:“上天被我的骄傲激怒了，我的证明是不对......”

——这就是装X遭雷劈，四色定理版。

库默尔(Kummer)是德国的顶级数论专家。他在研究费马大定理的时候，创立了理想数理论——这个理论甚至比费马大定理本身还重要。

然而，作为一个顶级数论大家，他在上课的时候竟然忘了九九乘法表……

一次上课，他需要在黑白上计算7×9……

“七乘以九，啊，七乘以九，……到底等于多少？”

“老师！”，一个学生举手回答道，“等于61。”

“老师不对！”，另外一个学生提出异议，“应该是67。”

“好了，好了”，库默尔说到，“肯定不可能两个都对，但那不重要了！——现在我们知道，两个里有一个是对的。”

古尔萨(Goursat)是法国著名的分析学家，复变函数里有柯西-古尔萨定理：解析函数在简单闭曲线上积分是零。

古尔萨对人很热情，但是讲课确实不咋地。他上课总是讲几十年前陈旧的东西，而且照本宣科，连说话的语气都不变。有一位波兰的学生，来到法国巴黎学数学，很不幸地选了古尔萨的课，感觉很不好。

由于和自己预期差距太大，这位学生感到自己精神受到巨大打击。想到自己大老远的跑到梦想的数学圣地巴黎来学数学，却只是听着这样的课程，这位学生竟然大哭起来……

这位学生叫做曼德博(Mandelbrot),著名的分形曼德博集合就是他的名字，后来他创立了分形几何学，人称”分形之父“。

武丁(Woodin)是美国院士，是当今集合论方向的领军人物，曾经在国际数学家大会上发表一小时演讲。

一次上课，他讲到一个东西需要一个引理，他说那个引理是显然的，因为A、B、C的条件。

“教授，A、B、C条件推不出那个引理，我能找到反例”，听课者举手说道。

“那这里还有D条件，有了D条件就可以了吧！”武丁教授说。

“依然不行！仍然又反例！”另外一个听众说。

“让我想想”，武丁说，“再让我想想……”

“——啊，我想起来了，这个引理本来是我留给大家的课后作业的！”

彭联刚是四川大学数学学院代数方向的教授。这个故事在川大广为流传，甚至还上过当地报纸《华西都市报》。

一次彭教授上课，突然有学生举手提出一个问题，大概是说如果修改一下某个问题的证明顺序，能让解决过程更简洁之类。

彭教授一听，严肃的收起了表情，说：“哦，还可以这样？让我想想。”

于是彭教授站在黑板面前紧锁眉头，开始思考。教室一片寂静……

五分钟过去了……

彭教授抬起头来，敲了敲黑板，说：“嗯，真的可以这样！让我再想想，再想想……”

又五分钟过去了……

下课铃响。

看见了吧，当数学老师多么不容易。如果你们身边有好老师，好好珍惜吧，要把数学教好实在太难了。

祝每一位老师节日快乐！

关注 哆嗒数学网 每天获得更多数学趣文

关注 哆嗒数学网 每天获得更多数学趣文

根据科学突破奖官网消息。被誉为“科学界的奥斯卡奖”的2020科学突破奖获奖者揭晓，其中数学方面由芝加哥大学的阿莱克斯·埃斯金(Alex Eskin)教授获得，将获得300万美元的奖金。

埃斯金教授与已故的伊朗裔女数学家、菲尔兹奖得主米尔扎哈妮合作，在阿贝尔微分的模空间的动力学和几何方面做出了革命性发现，包括证明了所谓的“魔杖定理（magic wand theorem）”。

另外，美国加州理工学院的朱歆文教授因其“在算术代数几何中做出重要工作”获得新视野数学奖，奖金10万美元。

朱歆文是北大数学科学学院2000级本科生，这是北大本科体系培养的数学家连续三年获得此奖项。在今年早些时候，朱歆文教授还获得有着“华人菲尔兹奖”的2019年度ICCM数学奖(前晨兴数学奖)。

科学突破奖为世界上奖金最高的学术奖项。值得注意的是早期此奖的赞助者有阿里巴巴创始人马云(Jack Ma)，而现在赞助名单中没了马云的踪影，而有了中国另外一位中国互联网巨头，腾讯公司创始人马化腾(Ma Huateng)。现在官网公布的赞助者是：由谷歌公司联合创始人谢尔盖·布林，Facebook创立者普莉希拉·陈、扎克伯格夫妇、腾讯创始人马化腾、俄罗斯互联网巨头茱莉亚·米纳尔、尤里·米尔纳夫妇与23andMe公司联合创始人安妮·沃西基。

此奖项共设立生命科学、基础物理、数学三大奖项。每个获奖席位300万美元奖金。另外，还为物理和数学的“学术新人”设立了科学突破新视野奖，每个获奖席位10万美金。按官网介绍，2020年的科学突破奖会有2160万美元的奖金发出。

关注 哆嗒数学网 每天获得更多数学趣文

关注 哆嗒数学网 每天获得更多数学趣文

还记得哆嗒小编发布的文章吗《人类第一次将33写成了3个整数的立方和》，描述了33被写成三个整数立方和的过程以及三立方和的问题背景。当时提到，100以内还没有写成3个整数立方和的数只有42了。——当然，严谨的说9n±4的这些自然数除外，因为它们不可能写成这样的等式。

而昨天有人在了麻省理工学院数学系的网页上贴上了一个等式，网页同样很简单，但没给出结果：
​

(-80538738812075974)^3 + 80435758145817515^3 + 12602123297335631^3

等于多少自己算？——他居然等于——等于42！

在推特上，菲尔兹奖得主高尔斯也转发了这个结果。

于是下面这句话成为定理：

除了9n±4型自然数外，所有100以内的自然数都能写成三个整数的立方和。

据悉发现此等式的数学家是来自布里斯托大小的Andrew Booker和来自麻省理工学院的Andrew Sutherland 。

如果有人要问，此结果有什么用？数学家们负责发现数学规律，有没有用之类的问题不是数学家必须回答的——但是搞这个本身很好玩不是吗？

这意味着，最小的没被写成三个整数立方和的自然数为114。

附上100以内三立方和的非零解全表（多种写法选取其中一个）

1 = (-1)³ + 1³ + 1³
2 = 7³ + (-5)³ + (-6)³
3 = 1³ + 1³ + 1³
4不可能
5不可能
6 = (-1)³ + (-1)³ + 2³
7 = 104³ + 32³ + (-105)³
8 = (-1)³ + 1³ + 2³
9 = 217³ + (-52)³ + (-216)³
10 = 1³ + 1³ + 2³
11 = (-2)³ + (-2)³ + 3³
12 = 7³ + 10³ + (-11)³
13不可能
14不可能
15 = (-1)³ + 2³ + 2³
16 = (-511)³ + (-1609)³ + 1626³
17 = 1³ + 2³ + 2³
18 = (-1)³ + (-2)³ + 3³
19 = 19³ + (-14)³ + (-16)³
20 = 1³ + (-2)³ + 3³
21 = (-11)³ + (-14)³ + 16³
22不可能
23不可能
24 = (-2901096694)³ + (-15550555555)³ + 15584139827³
25 = (-1)³ + (-1)³ + 3³
26 = 297³ + 161³ + (-312)³
27 = (-1)³ + 1³ + 3³
28 = 14³ + 13³ + (-17)³
29 = 1³ + 1³ + 3³
30 = (-283059965)³ + (-2218888517)³ + 2220422932³
31不可能
32不可能
33 = 8866128975287528³ + (-8778405442862239)³ + (-2736111468807040)³
34 = (-1)³ + 2³ + 3³
35 = 14³ + (-8)³ + (-13)³
36 = 1³ + 2³ + 3³
37 = 50³ + 37³ + (-56)³
38 = 1³ + (-3)³ + 4³
39 = 117367³ + 134476³ + (-159380)³
40不可能
41不可能
42 = (-80538738812075974)³ + 80435758145817515³ + 12602123297335631³
43 = 2³ + 2³ + 3³
44 = (-5)³ + (-7)³ + 8³
45 = 2³ + (-3)³ + 4³
46 = (-2)³ + 3³ + 3³
47 = 6³ + 7³ + (-8)³
48 = (-23)³ + (-26)³ + 31³
49不可能
50不可能
51 = 602³ + 659³ + (-796)³
52 = 23961292454³ + 60702901317³ + (-61922712865)³
53 = (-1)³ + 3³ + 3³
54 = (-7)³ + (-11)³ + 12³
55 = 1³ + 3³ + 3³
56 = (-11)³ + (-21)³ + 22³
57 = 1³ + (-2)³ + 4³
58不可能
59不可能
60 = (-1)³ + (-4)³ + 5³
61 = 845³ + 668³ + (-966)³
62 = 3³ + 3³ + 2³
63 = 7³ + (-4)³ + (-6)³
64 = (-1)³ + 1³ + 4³
65 = 91³ + 85³ + (-111)³
66 = 1³ + 1³ + 4³
67不可能
68不可能
69 = 2³ + (-4)³ + 5³
70 = 11³ + 20³ + (-21)³
71 = (-1)³ + 2³ + 4³
72 = 7³ + 9³ + (-10)³
73 = 1³ + 2³ + 4³
74 = (-284650292555885)³ + (66229832190556)³ + (283450105697727)³
75 = 4381159³ + 435203083³ + (-435203231)³
76不可能
77不可能
78 = 26³ + 53³ + (-55)³
79 = (-19)³ + (-33)³ + 35³
80 = 69241³ + 103532³ + (-112969)³
81 = 10³ + 17³ + (-18)³
82 = (-11)³ + (-11)³ + 14³
83 = (-2)³ + 3³ + 4³
84 = (-8241191)³ + (-41531726)³ + 41639611³
85不可能
86不可能
87 = (-1972)³ + (-4126)³ + 4271³
88 = 3³ + (-4)³ + 5³
89 = 6³ + 6³ + (-7)³
90 = (-1)³ + 3³ + 4³
91 = 364³ + 192³ + (-381)³
92 = 1³ + 3³ + 4³
93 = (-5)³ + (-5)³ + 7³
94不可能
95不可能
96 = 10853³ + 13139³ + (-15250)³
97 = (-1)³ + (-3)³ + 5³
98 = 14³ + 9³ + (-15)³
99 = 2³ + 3³ + 4³
100 = 7³ + (-3)³ + (-6)³

关注 哆嗒数学网 每天获得更多数学趣文