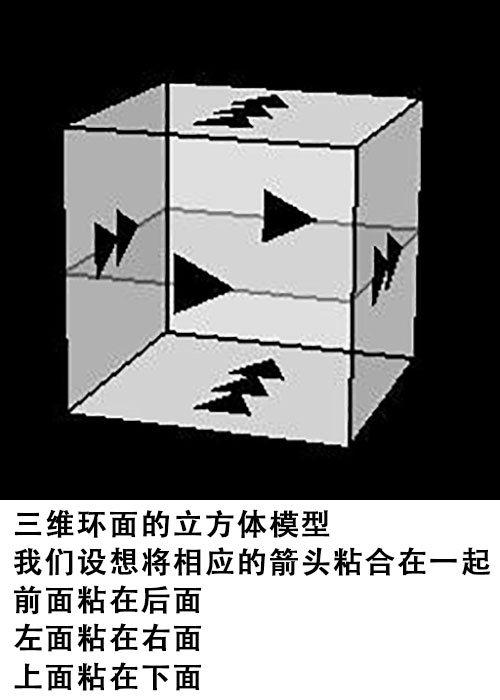
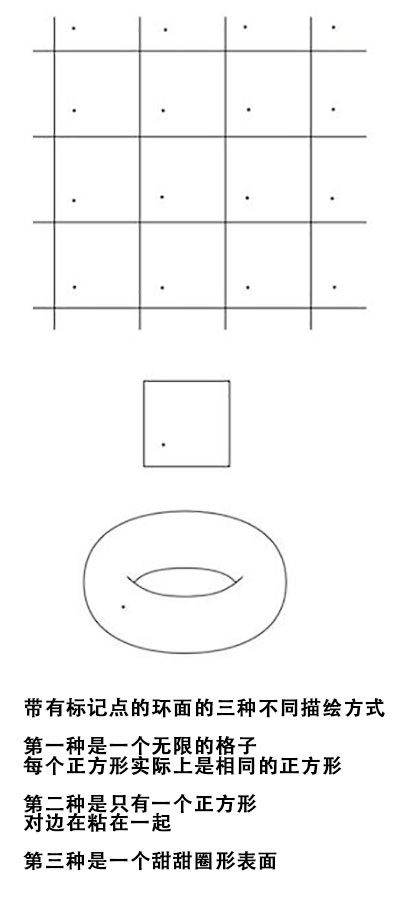
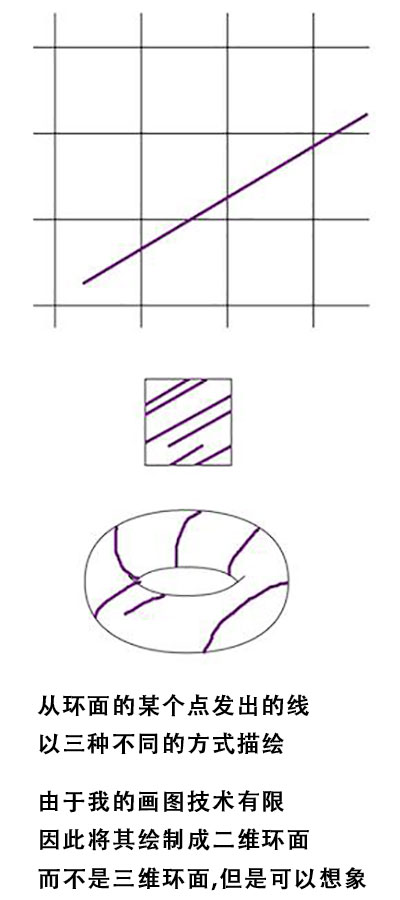
计算小错误,人间大灾难:六个数学“小”错误导致的人间惨案
关注 哆嗒数学网 每天获得更多数学趣文
如果有小朋友在阅读这篇文章,那么一定要记得一件重要的事情:在大人的世界里,哪怕一点点微小的计算错误,都将可能导致严重的后果,甚至会闹出人命!
如果你不相信,那么下面我们会分享几个真实案例给你。在这些案例里,无一不是如此。
案例6: 方形窗引发航班坠毁

在20世纪50年代,很多公司首次进军喷气式客机,领先的是德哈维兰公司。该公司制造的“彗星”号喷气式客机运用了很多先进技术,从而使飞机拥有很多前所未有的特性,比如增压舱的加入可以促使飞机比别的非得更高更远等等。

或许是因为“彗星”实在不是个好名字吧,在1954年,两架“彗星”飞机在空中莫名解体。这场事故共夺去了56人的性命。
事后查明,事故原因令人惊讶的简单:飞机采用了方形窗设计!
在众多明显而又容易被忽略的因素中,方形窗的设计就是其中之一。当时的飞机设计师就是忽略了这一点。观察下面的奇巧巧克力的条图片,你看出了什么?是不是觉得稍微用点力这些巧克力就会从中破开?

飞机残骸上那些方形窗锋利的斷口清楚的表明了事故原因:这些巧克力式的方形窗带来的结构缺陷没能及时被发现。
如果要在墙体上安装方形窗,需要造出四个90°的角,这会导致四个弱支撑点的出现。如果你的房子由砖块或者灰泥来建造,无需任何复杂计算,只需走到房子外面看看就会发现,沿着每个90°角的顶部会出现清晰的裂缝。

在工程学中,类似奇巧巧克力条间的沟槽会用一个专业术语——“应力集中”来描述,意思是,在压力下更可能断裂的地方。
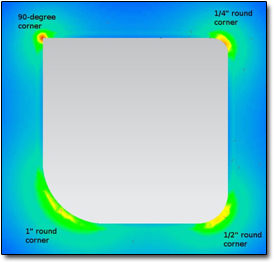
如果你是飞机制造商,怎么解决这个问题呢?
在你乘机出行的过程中,你是否注意过飞机上的窗口其实都是圆角的?这些弧形曲线几乎是能够防止飞机发生空中解体最完美的形式了,就像搏击台上的圆形绳索护栏一样,它将应力分布到沿圆形曲线的所有各个点,而不是在一个尖锐的拐角上,这样就可以有效防止其随着时间的推移而分裂并形成裂缝。
相信我,这其实并不是一个容易说清楚的问题,专家们也是在对机舱结构重复进行了很多次压力测试后才得出这个结论的。试验结果证明,如果采用方形窗的机舱,裂缝就会从窗户的拐角处产生并逐渐扩大,最终会导致窗户像冒牌避孕套一样爆裂。
波音公司和道格拉斯公司的代表们都表示,他们的工程师们也未预料到该类事件的发生。如果不是彗星飞机第一个发生坠毁,那么他们的公司或许就会成为因采用方形窗设计而发生该类事故第一家。从那时候起,飞机的窗户都被设计为圆角。

案例5: 跑道角度引发的战斗机坠毁事故

由于航空母舰(以下简称航母)船体随着海浪上下摆动,航母上众多飞机又拥挤在一起,给在航母上能够降落的飞机留出的空间异常狭小。所以即便不是飞行员,你也能够想象到在航空母舰上降落实在是一件非常困难的事情。但请放心,航母上拥有众多辅助设备、计算机和各类指示信号来引导飞机降落。然而,早期的飞机可没有这样的待遇,它们遇到的是另外的问题。
可笑的小瑕疵:这里有张图会告诉你早期的航母是什么样子的。你是不是觉得简单的不像话?它上面只有一条直直的跑道。设计这条跑道的人不知道怎么想的?

这种设计简直无异于让飞行员去自杀。如图所见,起飞的飞机正好占用了准备要降落的跑道一端的位置!如果不及时刹车停止,双方的飞机只能变成一团火球。然而及时让降落的飞机停下来可不是小事一桩,光是勾住拦阻索(一种能够使飞机快速停下的装置)就是很高难度了。经过了血与火的教训后,航母设计最终采用了当时看来似乎有些不合常规的方案,并加装防护网,确保飞机即便没能抓住所有拦阻索,也能及时减速停止。对于飞机来说,类似装置只是确保飞机能够利用障碍物及时停止的众多非凡措施之一。

那么,问题来了,为了确保飞机在航母上安全降落的最棒的革新是什么?答案是:把跑道旋转了9°重新设计。如下图:

好笑吗?其实一点也不,这可是花了很多年时间在研究出来的。在历史的长河中,很多伟大的技术进步,包括像航天器和原子结构等研究,都是在二战中诞生的。直到1952年,人们才想到要更改飞行甲板的角度。在此之前,任何一次降落,简直就是飞行员末日折磨。

调整飞行跑道的角度可以让飞机的降落和检修工作得以同步进行。然而在二战中,如果一架飞机正在降落,那么另一架飞机就不得不推迟起飞,反之亦然。如果10年甚至更早以前有人能想到这个解决方案,不知道会拯救多少人的生命啊!
案例4: 意外改动引起的走廊坍塌事故

凯悦酒店集团在对建在堪萨斯城的最新酒店设计单位提出要求,希望将所有的警铃及口哨包含在内。负责进行设计的建筑公司给出了一系列的空中走廊方案。这些走廊悬挂在顶部,以便于为客人提供最佳的观赏角度。总之,这个设计为酒店带来异常吸引人的特色,直到它有一天发生了突然坍塌,使100多人当场送命。

事故原因异常的简单:一条长承重梁被两条短的代替了。
在日常活动中,人们总是倾向于选择阻力最少的那条路。(换言之,如果能够从杂乱无序的工作中摆脱出来,人们一般就会选择这样做)。在最初的设计图中,两条空中走廊一条在另一条的上面,两条空中走廊都被一条长长的承重梁支撑着,这个承重梁用螺钉紧紧固定在顶部。就像下图(a)所示:
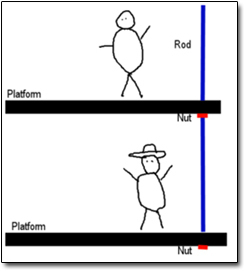
看起来相当简单明了,对吧?走廊悬挂在长长的承重梁上,这既能使它更坚固,也能使它受力较为均匀,承重梁穿过两条走廊后,一直延伸到顶部的天花板。
一般来说,大部件使用起来要费事一些。这很容易理解,如果要搬一把椅子到房间里,整体搬总要比搬一箱配件更费事些。这些长长的承重梁需要穿过很长的空间才能到达顶部固定它们的平台。
这样的承重梁制造起来可是比较困难,那就选更容易的方式,对不?所以,负责生产这些承重梁的钢铁公司作出了一个小小的改变,用两条短承重梁替代一条长承重梁,如下图中(b)所示。
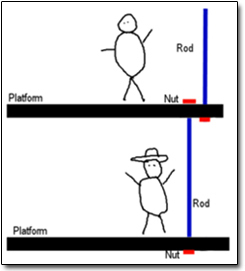
这样便于加工,便于安装,看起来是一样牢靠,对吧?但这个小小的改变产生的待见是牺牲了114人的性命,216人受伤,外带高达1亿4千万美金的诉讼索赔。
一条承重梁,两只螺钉。每个螺钉只需要承载自身所在平台的重量。这是个好方法,因为每个螺钉(以及与螺钉连接的焊接梁)只需要承载一个平台的重量。现在再来上图中(b)。怎么样?看到这样脑残设计,你想不想爆粗口?
现在可以清晰的看到,每个螺钉都必须承受两个平台的重量,并且是在那些劫数难逃的参观者们站在上面的情况下!看起来是不是非常明显?祝贺你们看出了这点,可当时任何一家公司里都没有一个专业人士意识到这一点。
接下来的某晚,在一场舞蹈比赛活动中,承受不住压力的螺钉从焊接梁上彻底断裂,空中走廊发生了坍塌。如下图:

然而在接踵而来的诉讼过程中,人们发现,无论是钢铁制造公司还是负责结构设计的工程公司都没有做哪怕一丁点粗略的计算,而这些计算会清楚的显示出这个显而易见的缺陷。
案例3: 向内开门方式引发的夜总会惨案

如果你曾置身在上世纪三四十年代的波士顿,并且你不是个古板无趣的家伙的话,那你一定去过“椰林夜总会”。它可是那个年代最炙手可热的城市夜总会,任何一个去过的人无不这样认为。OK,所以嘛,有时候那儿就会显得狭窄些,会有尽可能多的客人涌入,如果碰上节假日,人数甚至会是正常情况下460人容量的两倍还不止。热闹之后,客人玩够了就会独自离开回家去了,那时波士顿所有地方都没有任何像警示牌一类的安全措施。
1942年,一场突发的大火夺去了492人的生命。事后调查发现很多人并不是死于大火,他们的死因竟然是因为门是向内开的!这样的解释简直简单到难以置信。

事情起因是一个勤杂工在黑暗中摸索着寻找电源插线板,他想看看他摸到了什么东西,于是他划燃了一枚火柴,这根火柴意外引燃了华丽的热带风格装饰品,而这些装饰品又非常易燃,结果很快俱乐部内到处都是浓雾和火苗。这场大火燃烧的非常迅猛,以致于事后发现一些人来不及放下手中的酒瓶就被火焰瞬间吞没了。
关于夜总会的安全隐患,你能想到严重超员和易燃物装饰,你或许没有想到过的另外一个可能都存在的严重缺陷:就是,逃生门是向内旋转开启方式。
主出入口因为安装的是旋转门,结果很快被想要出逃的人群给堵的结结实实。于是人群蜂拥至另一个出入口,结果前面的人被后面的人推搡着狠狠压在门上,导致门无法打开。据事后估算,如果在这场大火中的出入口的门是在外向锁闭的,那么至少会有300人能够逃出生天。

不幸的是,这不是第一次(也不是最后一次)因为向内开启的门引起的恶性事件。易洛魁剧院大火、湖景文法学校火灾、纽约三角内衣工厂火灾、贝弗利山庄大火和杜邦广场酒店纵火案等等因为火灾导致人员重大伤亡事故中,无一例外的发现出口的门都是向内开启方式。如果你认为看了则事故后,你会近乎于偏执的检查最近的逃生门的开启方式,那么别担心,我跟你也一样。
案例2: 密不透风的塔科马海峡大桥崩塌事件

塔科马海峡大桥曾被誉为工程学一个靓丽的范本,直到它崩塌落入塔科马海峡,并夺走了一条狗的性命。这条狗是因为感受到主人的恐慌情绪而离开轿车的,但它的主人明显并不是很慌张,他还有时间拿出相机记录下了这一不幸事件。

在工程人员和物理专业学生眼里,塔科马海峡大桥毫无疑问是一个教会他们做什么和如何做的教科书般的例子。如果你想把一件足够大事物固定好,那么没有人会忘记这个事件的教训。说了这么多后,你可能在想这座大桥究竟什么地方出了错?

原因依然很简单:桥上没有孔洞。
薄薄的大桥看起来会是怎样的?下面,通过这个事件你会清清楚楚的看到。
你或许想说桥的倒塌是因为廉价和少用了钢材,但事实上的原因很清楚:不透风!
无论建筑如何坚固,它依然会随风轻轻摆动。著名的迪拜哈利法塔(就是汤姆·克鲁斯在电影谍中谍里曾经摇晃着走过的建筑)在大风天里摆动幅度会达到6英尺。你可以自己算算。
塔科马海峡大桥压根就没有孔洞使风能够通过,那么为此它吃尽苦头注定无法避免。

其实在事件最初,人们就知道会有什么事情要发生。只要有风,风就会紧紧压迫桥面,像摇油漆罐似得摇晃它。桥面上下摆动的幅度达到好几英尺,就像随时要掉入河床似得。桥面随风扭动的非常厉害,以至于当地人戏称它为“飞驰盖地”。
更糟糕的是,风导致的摇摆频率接近桥本身的固有频率,这可是异常危险的状况。意识到情况的严重性后,州政府聘请工程专家想要修正这个错误。专家给出的方案包括在“桥面上钻多个孔洞用来通风,从而防止桥体的扭曲。非常简单的修复方式,我敢打赌他们一定为自己没能早些想到这些而憎恨自己的愚蠢。然而,在还没来得及付诸实施任何修复措施之前,桥塌了。

他们不得不在十年后重建了这座桥。下面看看,你是否能够找到设计中这些简单的不同点。

案例1: 泰坦尼克号的沉没

关于如何防止泰坦尼克号的沉没事件,有很多种说法。其中有人认为应该让船体直接撞向冰山上而不是试图绕过它,还有人认为原因在于首航前没有认真向上帝祷告,说什么的都有。人们对该事件的指责大多落在了缺乏足够的安全措施这一点上,这是非常错误的,真正的原因时是存在一个被刻意设计出来的潜在缺陷。

这个缺陷就是:中央推进器无法反转。
泰坦尼克号拥有三个蒸汽推进器,外侧两个以活塞引擎驱动,中央一个以蒸汽涡轮驱动。蒸汽涡轮相较于活塞结构具有体积小和更高效率的优势,但它的缺点是单向工作,也就是说,蒸汽涡轮只能向前转动,带动的传动杆也只能向一个方向运动。

所以,当危险来临是,当默克多大副想要操作船体全力后退以避免撞向冰山的时候,外侧的活塞引擎开始反向转动,而中央推进器却停止工作了(就像电影里的情节一样)。从常识上来说,如果你需要船体后退,你肯定不希望船体任何一个引擎把船体往前推。
不妙的是,中央推进器正好位于船舵的正前方,它的关停会使船舵少量进水,导致对任何操作的响应被拖慢。
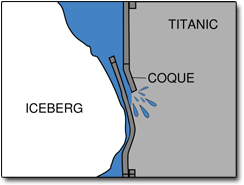
如果当初能够对中央推进器进行更合理的设计,就完全可以避免它反转时会停止的情况,那么泰坦尼克号就有可能逃过冰山的撞击,从而挽救1514人和8条狗的生命。
关注 哆嗒数学网 每天获得更多数学趣文