数学家证明了低维度空间的一些对称性质不存在

 

原文作者，Kevin Hartnett，《量子》杂志高级编辑。

翻译作者，独行者，哆嗒数学网翻译组成员。

校对：Math001

 

关注 哆嗒数学网 每天获得更多数学趣文

 

罗伯特·齐默(Robert Zimme)先生被人另眼相看了。自2006年担任芝加哥大学校长开始，他因为获得九位数字的捐款以及发表很多关于保护校园言论自由的文章而登上各大报纸的头条。但在担任芝加哥大学校长之前，齐默先生是一位数学家。在他将学术研究放到一边很久以后，齐默先生曾经推动的研究终于产出了成果。

 

 

2017年，一个三位数学家组成的团队解决了名为齐默猜想的问题，这个问题主要是研究在某些情形下几何空间会显示出某种特定的对称性。他们的证明是近几年来最大的数学成就之一。这个问题是齐默在20世纪70年代后期到20世纪80年代前期学术活跃期间提出的，现如今这个问题得到了解决。

 

齐默说，“我想说的是，在这五年期间，我对这个问题日思夜想，它每一天都在困扰着我。所以，这个问题让我辗转反侧。现如今，我很高兴地看到这个问题得到解决。”

 

一般而言，我们通常认为几何空间的维度越多，对称性特征也就越多。比如，你可以去比较二维平面上的圆和三维空间中的球：旋转球的方法就比旋转圆的方法要多得多。这就是因为球的额外维度使得球有了更多的对称性。

 

齐默猜想关注点主要是在某种特定类型的对称性，这通常被称之为高阶格(higher-rank lattice)。这个猜想关注了以下问题：一个几何空间的维度是否会限制对这些类型对称性产生。芝加哥大学的阿伦·布朗教授(Aaron Brown)和赛巴斯提安·乌尔塔多·萨拉查教授(Sebastian Hurtado-Salazar)和印第安纳大学的大卫·费希尔教授(David Fisher)的最新研究表明，只要低于某一维度，某些特殊的对称性就不可能存在。这也就证明了齐默猜想是正确的。

 

 

他们的研究解决了一个长期以来困扰数学界的问题，同时也开辟了新的研究方向。它揭示了几何空间中的内在特性。对称性是了解这些空间最基本的特征之一。这项新研究可以用比较准确的话来讲：这些对称特征能存在某一种空间中，但对于其它空间是不存在的。齐默猜想长达数十年间都没有取得突破，现在解决以后，数学家们便有了新的发现和成就。

 

在今年年初组织的一场关于新证明的会议上，芝加哥大学数学教授艾米·威尔金森(mie Wilkinson)表示：“这个猜想还能够让数学界研究和分析上很长一段时间。他们就这个问题提出了一个较为简单的方法。”

 

对称性的满足

 

对称性是人们从孩提时期的数学中便接触到的几何学概念。通过动手分析，孩子们便知道由于对称性，图形可以旋转、翻转和平移，最后得到的图形和最开始是一致的。图形的这种在变化中保持不变的特性满足了某种内在特点——它揭示了宇宙法则中的某种深刻涵义。

 

在数学中，数学家们用自己特定的规范性语言来研究对称性。这种语言为他们提供了非常准确的方法来描述在给定的几何空间中所有不同的对称性。

 

比如说，正方形有八个对称变换——也就是说有八种方法可以将正方形翻转、旋转成原来的图形。而对于圆来说，圆按任意角度旋转之后仍然是圆；它有无数个对称变换。数学家把特定几何对象或空间所具有的对称性全部归类在一起，称之为“群”。

 

群原本就是非常有价值的研究对象。群通常会出现在特定几何空间的研究中，但是他们也会出现在非几何领域中。比如，数的集合也可以组成群。（比如说：考虑如下的对称性,例如给一个数+5或-5。）

齐默说：“理论上，各类事物的对称性都可以用群来表达。”

现在我们讨论的对称性和我们在小学时所学到的相差甚远。比如，参考格的对称性。最简单的格就是一个二维网格。在平面上，你可以将这块网格往上、下、左、右的方向平移任意方块的距离， 然后得到一个它完全一样大小的网格。你还可以对网格内任何单独的正方形进行对称变换。这种有类似格的空间，一般而言会有无穷个多种多样的对称变换。

 

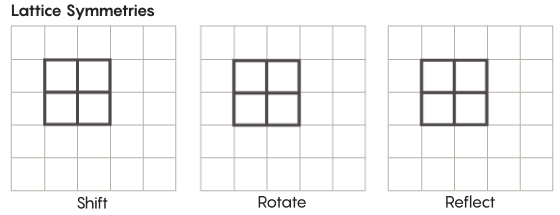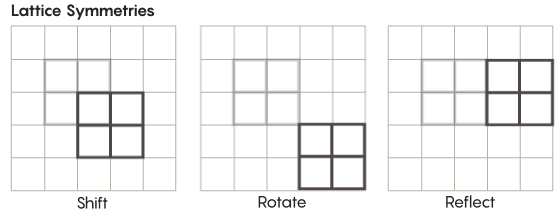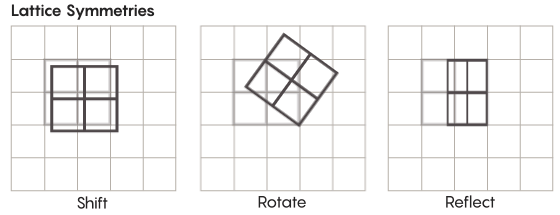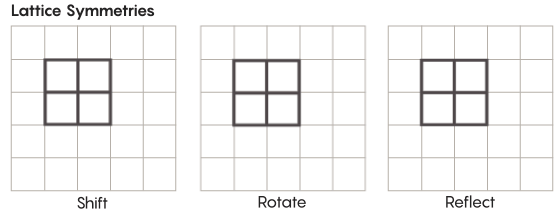
这种可以存在任何维度的空间里。在三维空间里，格就是一个个正方体，而不是正方形。在四维或更高维度的空间里，我们就无法画出这种格了，但是性质是一样的。数学家可以用自己的语言进行准确描述。齐默猜想的关注对象主要就是这些特定维度的。“如果你可以看到这些网格，这些奇怪的格会特别美丽。尽管我看不到。”乌尔塔多-萨拉查教授说，“我猜想如果它们能展现在我们眼前，他们的形状一定特别好看。”

 

早在二十世纪，数学家们便在许多的领域中发现对称性质，不仅在几何学，还有数论领域，逻辑学和计算机科学。当新的一个新群被发现以后，我们就自然而然地会问到——一个怎样的空间会对应这个群描述的对称？

有时候是非常明显的，一些群不能应用到特定的空间中去。比如，我们就很快知道圆的对称群不能应用到正方形中。就比如说，如果将正方形旋转10°，你就不能得到原来的那个正方形了。但是如果在一个有无数个对称轴的群中和一个有多重维度的空间里进行研究，我们很难确定哪些群的元素对应着空间的变换，而哪一些则不是。

齐默说：“由于在高维度的情况下，你由此得到的群会愈发复杂，问题的解决也就变得更加困难。”

松散的联系

当我们分析对称性的时候，我们所想象到的是，整个图形正在进行旋转，就像一个正方形按顺时针方向转90°。在一个比较微观的层级中去观察，对称性与点的运动有密切的联系。按对称性将空间进行变换意味着将空间上的每一个点移动到空间的另外一处。在这种视角下，将正方形顺时针旋转90°的真正意义是：考虑正方形上的每一个点，然后将它顺时针旋转90°，这样每个点就移动到了新的边上，这些点最终出现在与初始位置不同的边上。

或多或少的，我们都是用刚性的方式来进行移动。最熟悉的一些对称操作——通过对角线进行镜面变换，或者旋转90°——都非常刚性的。他们之所以刚性的是因为他们并没有对点进行扭曲。镜面变换前在顶角上的点在变换以后还是顶角上的点（只不过是不同的顶角），镜面变换前在边上的点在变换以后还是边上的点（只不过是不同的边上）。

 

但是，在实际上，还有很多更为灵活的对称变换类型，这也是齐默猜想所感兴趣的地方。在这些变换中，点会被最大限度的重组；他们在变换的过程当中不会完全遵循他们在变换前的位置关系。例如你可以将正方形的每一个点都围绕着移动三个单位——这还是满足了一个对称变换的基本要求，它将空间上的每一个点都移动到了新的位置。新证明的合作者艾伦·布朗借助球的模型来解释这种不受约束的变换方式。

 

布朗称：“你可以试着将球的南北两极向相反方向拉扯，球上的距离和点之间的距离会加大。”

 

当你在讨论一个网格时，除了平移平面中的网格，你还可以对网格进行扭曲，或者在某些地方进行扭曲，而在其他地方进行拉伸，这就使得转换后的网格不再与原来的网格完全重合。这些变换就没有那么刚性了，他们被称之为微分同胚。

 

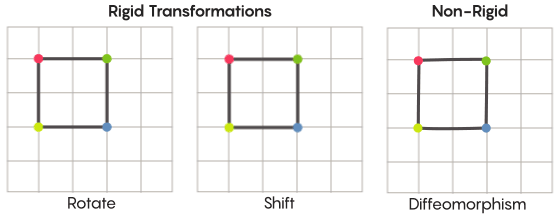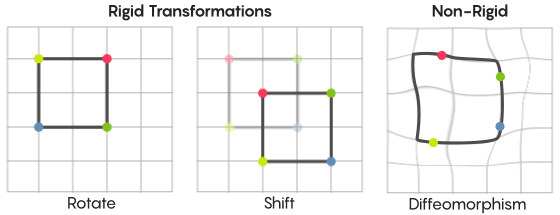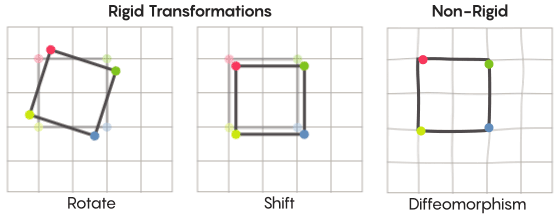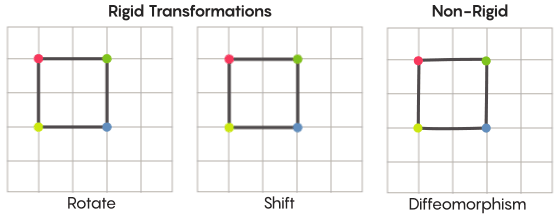
在他的猜想当中，齐默有非常好的理由认为这种更为柔性的变换是有意义的。在20世纪60年代，格里戈里·马尔古利斯(Grigory Margulis)对在齐默的猜想当中涉及的这种高维格进行了研究。马尔古利斯也因为这项工作由此获得了菲尔兹奖。当要求只进行刚性的变换时，哪些空间可以由这些高维格转换而来，马尔古利斯给出了这种空间所有满足的条件。

因此，齐默猜想是对马尔古利斯研究的自然延伸。他便是开始于高维格架构变换得以实现的空间——马尔古利斯所找到的空间——并持续深入探讨如果允许不那么刚性的变换，也就是在放宽变换的条件之后，这个集合是否会进一步扩张。

在他们新的研究当中，三位数学家们证明了当高维格的放宽对对称性的定义以后，广义的对称性特征并没有本质变化。即使格进行不规则的空间变换时——比如剪切、弯曲、拉伸——高维格仍然被限制在它们所在的空间中。

 

费希尔说：“由于在这个问题上加了那么多的灵活性之后，你就有了一种直观的感受，这些高维格群能作用于任何空间上。所以，我们很惊讶的发现，答案是不对的。在某种情况下，他们不能作用于任何空间上。”

这几位数学家们在空间的维度和能作用在其上的高维格维度（或秩）之间建立了联系。他们证明了在通常情况下格的维度越高，空间的维度也应该越高，这样才能对格的对称性产生作用。在高维空间里，即使有非常好的空间变换灵活性，高维格的变换依旧受到高维空间的限制。

威尔金森说：“这就告诉了我们，空间将物体组合在一起会有一些非常基础的特性，这种特性使得他们能够产生这些变换。”

 

齐默猜想只是解决一个大问题的第一步。通过解决这个猜想，这个问题的研究者们对这些高维格能做用的空间给出了一个粗略的限制条件。下一步是更加宏伟的计划，研究者将关注在这些空间中格是如何出现的，接着将这些格在空间中变换的方法进行分类。

 

齐默说：“这项计划最后是要分清楚所有这些方法。在你目前所看到的问题之外还有更有趣的，有一些空间中，格是不能保持对称性的。但有趣的问题则远远超出了这些内容。”

 

 

关注 哆嗒数学网 每天获得更多数学趣文