既“大”又“小”的康托尔集

 

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，金星光，哆嗒数学网翻译组成员。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

康托尔集很庞大，但它当中几乎不含有任何“内容物”。

 

上个月，我写了关于π-Base网站的一些文章，这个网站与《拓扑学中的反例》这本书起着相似的作用。碰巧这学期我教授拓扑学这门课程，因此去回顾这些有价值的反例是件有趣的事情。作为博客上的一个新系列，我将会写一些看似怪异但不乏趣味性的数学空间的文章。我们就以康托尔集开始吧，这个有用的空间一直活跃在全世界的数学领域中。

 

通常有两种主要的方式来思考和理解康托尔集，我们先以第一种比较有趣的思考方式开始吧。我们先画出一条从0到1的线段，并且包含端点，因此我们得到闭区间[0,1]。现在我们将这个区间三等分，去掉中间的开区间(1/3,2/3)，然后我们就会得到[0,1/3]和[2/3,1]这两个闭区间。接着我们分别从中间去掉[0,1/3]和[2/3,1]这两个区间中间的1/3，我们就会得到[0,1/9]、[2/9,1/3]、[2/3,7/9]和[8/9,1]这四个区间。如果我们按照以上的方式继续做下去的话，我们就会得到康托尔集。

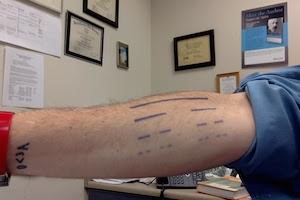
可能稍微令人惊奇的是，当你继续上述的所有步骤之后，几乎没有什么东西剩下。但是如果你进一步的思考，你将会发现0 , 1/3 , 2/3 , 1以及子区间的端点并没有被去掉。更令人惊讶的是，不仅仅是这些端点，还有非常多其他点, 因为端点数量只有可数个，但是整个康托尔集却是个不可数的集合。想要弄清楚原因，就让我们以另一方式来重新思考康托尔集吧。 

 

第二种描述康托尔集的方式虽然有些枯燥但会更加精确。我们通常以十进制来书写数字，但除了这种书写方法以外我们还可以以三进制来书写数字，这就意味着我们只需要数字0、1和2就可以了（十进制书写的1到10如果以三进制来书写就会写成1、2、10、11、12、20、21、22、100、101）。康托尔集是闭区间从0到1的数字中，那些在三进制中仅用0和2书写的数字的集合。例如，0是包含于康托尔集中的，至于1可以被写成0.22222....(就像0.9999...=1那样)。

 

用三进制的方式来思考康托尔集特别自然地符合康托尔集的构造。将闭区间[0,1]中的所有数字用三进制转换。当你去掉区间(1/3,2/3)，你就同时在去掉这个集合中三进制小数中第一个小数位为1的点。当你去掉剩下区间的1/3，你就同时在去掉三进制小数中第二位小数为1的点，以此类推。但我们确实要对端点值小心。早期的时候，我们注意到数字1可以被写成1或0.2222...类似地1/3可以被写成0.1或者0.0222222...。任何用三进制书写的数字如果以1收尾都可以用2的无限循环来代替，康托尔集是三进制中仅用0和2表示的数的集合，但这并不意味着这个集合中的所有数字一定要按照这种方式来书写，因此我们允许1、1/3以及诸如此类的数字成为这个集合中的一部分。

 

康托尔集并不仅仅是一个可以纹在身上的炫酷的事物，它也拥有许多很好的性质出现在早期的拓扑学和分析学的课堂上，你也可以用它来测试一些拓扑学和分析学中的一些新的定义。它将“大”和“小”的特性有趣的结合到一起。我在前文提到康托尔集是个不可数集。在去年夏天我写过一些有关不可数集合的文章。可数集的定义依赖于集合中的元素可列，即使我们不能写下整数集所有的元素，但是我们能够想出一种方法去列出它们，知道每个整数将会出现在数列中的哪个具体的位置上，因此整数集是可数的。令人吃惊的是，一些看似很大的集合依然是可数的。最令我吃惊的要数有理数集啦，有理数集理应要比整数集“大”，但准确来说，有理数集与整数集具有相同的元素个数。

 

实数集是不可数集。这意味着任何我们想要列出这个集合所有元素的方法都将以失败告终。康托尔的对角化论证，完美的证明了这一点，这是我最喜欢的数学证明。同样的方法可以证明康托尔集是不可数的，事实上它与实数集的元素个数相同。

 

这就是康托尔集开始成为反例开始的地方。它是不可数的，但它也没有包含任何“内容物”。它的长度是零。一种方法去注意到这一点是在于你每一步都去掉剩下某个区间长度的1/3.第一步，你去掉闭区间[0,1]这个区间长度的1/3，第二步你又去掉剩下区间长度的1/3，总共去掉了2/9.你去掉的长度总和是1/3 + 1/3 × 2/3 + 1/3 × 4/9 + 1/3×8/27 + …很容易的计算出这个几何级数的和为1。而这个区间的长度为1，我们去掉1个单位长度，最后却得到了多达整个实数数量的康托尔集。

 

如果你想要了解更多有关康托尔集的知识，π-Base列出了很多它的拓扑性质：它是紧致，完全分离，拓扑完备，非无核集(无核集定义：非空闭子集必有孤立点——编者注)。Cut-the-knot math有更丰富的有关康托尔集的知识，Robert Vallin(上述图片中有康托尔集纹身的人) 写了一本有关康托集的书。祝大家阅读愉快！

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa