它是一条连续的线却能填满空间

 

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，独行者，哆嗒数学网翻译组成员。

校对，donkeycn。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

铺满空间的曲线，一张在空间维度中具有跨越维数的谜图，他有着惊人的现实应用。

 

 

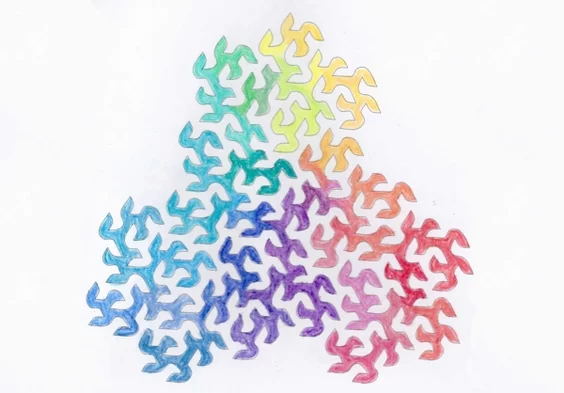
停下来看看这个独特的现象吧。想看一条能铺满空间的曲线的图像？看吧，就在下面！

 

 

啊，你一定会认为我是个逗比吧！一条可以铺满空间的曲线就好像说：一条线可以乱画，然后弯折便能铺满一个2维的区域，在这个例子中便是一个正方形。（同样地3维，4维空间的曲线也是如此，一条线可以铺满你所给的空间！）

铺满空间的曲线在他们的完整形态上并没有什么特别的特征。你可以从黑色实心正方形中学到什么？相反地，就像其他的分形，我们通常可以认为铺满空间的曲线可以是一个有限步的构造的无限版本。

 

有多种利用迭代来构造铺满空间的曲线的方法，这里是其中一种的动画版本（其实是希尔伯特曲线）。

 

 

在每一步，线中的每一段都被一个四段的折线所替换。这个过程中的每一条曲线都不能铺满整个空间，然而如果我们想象一下，这个过程要是可以一直持续下去，那么最终我们得到的那个无限版本就可以铺满整个空间了。

铺满空间的曲线挑战了我对维度的直觉。一条铺满空间的曲线就是一条直线的像，这一普通的一维对象，却可以铺满整个平面，这一普通的二维对象。这感觉就像是一个规规矩矩的函数，就不应该把一个一维的东西“映成”一个二维的东西一维便是一维，二维就是二维，两者毫不相干。不过还好，它只存在于无穷的情况，只是仍然有些让人不安。

（如果你正在学拓扑学课程，你可能会非常紧张。线和平面是拓扑上是不等价的，但是一条铺满空间的曲线却是一个连续的函数，他将线“映成”平面。这是怎么回事呢？难道，数学根基的错误被我们发现了？）

很难想象这种如此抽象化的弯曲程度近乎无限的线会在现实世界中有什么联系。但是事实上，充满空间的曲线让一维空间“映成”二维甚至多维空间的方法在数据处理中有许多现实应用。在这个非常奇妙的视频中，Grant Sanderson解释了一种能充满空间的曲线，希尔伯特曲线，是如何帮助我们寻找到一种最优的途径将一个图像的二维可视化数据转为一维声音数据。（B站传送门：https://www.bilibili.com/video/av4201747/index_2.html#page=1）

如果你想在自己的电脑里实现，这里有许多方法生成你自己铺满的空间曲线。如果你想投机取巧的话，只需要涂满一些方块。如果你对如何实现使用迭代方法来构造铺满空间的曲线，你可以遵循Vi Hart的方法来画龙形曲线，而Andrea Hawksley（她的灵感来源于Kyle Calderhead）将帮助你编织一条属于你自己的以希尔伯特曲线为图案的毛毯。

 

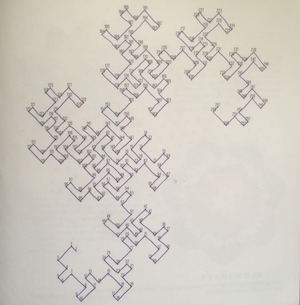
对于我而言，我在一本以数学为主题的绘本《Patterns of the Universe》中寻找到了属于我自己的铺满空间的曲线的奥妙。在他们的书里，有两页画了铺满空间的曲线。一条是在封面上显示出来的，而另一张则在下面，是用线将点连起来的图形。

在这个星期的前半部分，我一直驳斥着一些人对数学教育的错误观点，而此时给一条舞动的蛇上上色就能使我的心归于平静。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa