无限耳环

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，donkeycn，哆嗒数学网翻译组成员。

校对，小米。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

拓扑学所关注的是压缩和拉伸，而不是距离。然而无限耳环展示了拓扑学和几何学之间微妙的关系。

拓扑学有时被称为是戴上啤酒眼之后看到的几何或者是没戴眼镜看到的几何。几何学研究各种形状：它们是如何位于空间中的，它们是如何与自己以及彼此之间相互作用的。做几何通常需要用某种方式来测量距离。而另一方面，在拓扑学中，你可以毫无顾忌地拉伸或压缩；所以，在一个拓扑空间中，任意两点之间的精确距离不是本质问题。然而有时候不经意间，几何就会出现。一个数学对象的几何性质会影响其拓扑性质。

 

无限耳环，有时也被称为夏威夷耳环，是我在拓扑中最喜欢的例子之一，因为它展示了几何学和拓扑学之间精妙的关系。

 

为了构造无限耳环，你可以从一个二维欧氏平面开始：先添加一个以(1,0)为圆心，1为半径的圆；再添加一个以(1/2,0) 为圆心，1/2为半径的圆；再添加一个以(1/3,0) 为圆心，1/3为半径的圆。继续这样做下去：无限耳环由所有以(1/n,0) 为圆心，1/n为半径的圆构成，其中n取遍所有正整数。

 

 

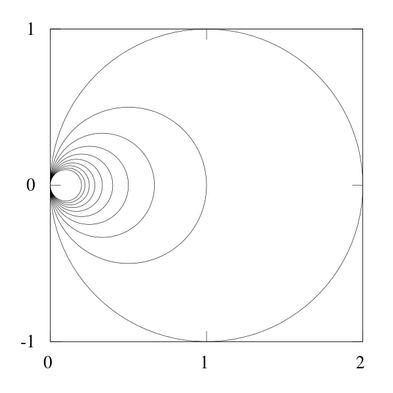
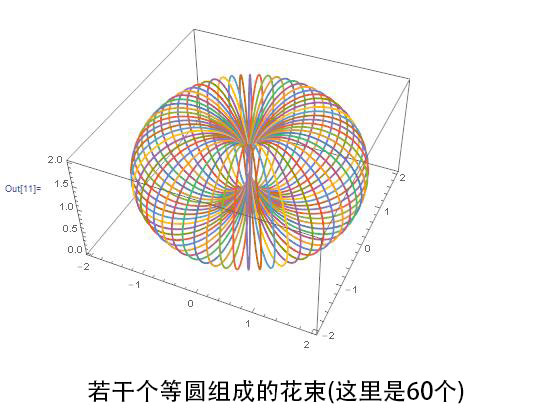
最终，你会得到一堆嵌套着的圆，并且它们恰好只有一个公共点(0,0)。当然事情并未到此结束。思考一下无限耳环它不是什么，这是很有教益的。例如，它不同于过同一个公共点的无穷可数多个相同大小的圆组合起来（我们称之为由可数多个圆构成的楔或花束）。这一事实可能会令人惊讶，因为毕竟，我们可以用不同的压缩比例来压缩那些圆，然后再把压缩后的那些圆压到同一平面内；或者也可以从另一个方向进行转换：通过吹胀无限耳环中的那些小圆至相同大小。尽管这些转换都很平淡无奇，但这两个空间并不完全是拓扑等价的。

 

圆本身也是一个拓扑空间，当我们谈论无限个圆时，我们并不要求它们位于任何特定的空间中。然而无限耳环却位于一个平面内，这就影响到了它的拓扑性质。我们无法将由可数多个相同大小的圆构成的花束形状放入一个平面内，因为这些圆将以我们不希望的方式产生重叠。

证明两个空间在拓扑意义下相同是很困难的，但只要有一个拓扑性质不同就能证明它们是不同的。证明无限耳环不同于由可数多个圆构成的花束的最简单的方法是：放大某些特殊的点的周围，然后看看你能得到什么。如果两个空间是拓扑等价的，那么当你在两者对应的点附件同时放大时，你会看到拓扑等价的东西。这两个空间最特殊的点就是所有的圆的公共点，即楔点。如果我们看一看这个点周围的一个小区域，我们就会发现我们想要找的差异。

 

在圆构成的花束中，楔点的一个小邻域由每个圆上一点的小邻域构成。它就像一把意大利面条。（“很多”根意大利面条。）

无限耳环上的点(0,0)周围的一个小的圆邻域是欧氏平面的一个小圆。它具有某个有限的半径，且该半径大于耳环内的某些圆的半径。事实上，它比其中的无数多个圆的半径都大。所以该小圆包含了耳环内无穷多个圆。也用面食来做比喻的话，它就是有限多根条状的面以及无限多根（很小的）圈状的面。

 

 

无限耳环和由圆构成的花束之间的区别还可以以其它复杂而宜人的方式表现出来，但我想我会把它们留待以后。现在，我打算再考虑另一个异于无限耳环的空间，而这个空间也是位于一个平面内的。

 

如果我们是向外构造圆，而不是向内，即它们具有整数半径1, 2, 3，等等（也许我们应该称它为更大的无限耳环）。我们得到了另一个与无限耳环完全不同的空间。有几个拓扑性质可以区分这两个空间。最容易看到的是：无限耳环是有界的而更大的无限耳环不是。

这两个无限耳环之间的另一个区别是：其中一个空间是闭的，而另一个不是。平面上的闭集有几个等价的定义。其中之一是：任何与集合中的点非常接近的点都在该集合中。更大的无限耳环不包含y轴上除(0,0)外的其它点，然而随着耳环中的圆越来越大，它们看起来越来越像一条直线，所以它们越来越接近y轴。当我们取遍整个空间的无限个圆时，y轴上的每个点都非常接近更大的无限耳环上的点，但它们每一个都不在更大的无限耳环上。

另一方面，较小的无限耳环就不存在这个问题。半径为1的圆是所有圆中最大的，所以该圆限制了y轴与所有圆接近的程度。

我花了一段时间来接受这样一个事实：无限耳环与圆构成的花束以及更大的无限耳环真的是如此不同，一个空间的几何性质真的可以对拓扑性质产生这样的影响。我想，在学习拓扑的人中，不是仅有我感觉自己只是在相信别人说过的话，却没有办法把它们真正内化。但在那种时候，我会用约翰·冯·诺依曼的一句话来安慰自己：“没人能理解数学，你只能是熟中生巧而已。”

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa