业余数学家发现最小万有覆盖

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，Math001，哆嗒数学网翻译组成员。

校对，donkeycn。

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

菲利普·吉布斯并不是一位专业的数学家。因此每当他希望深入探究一个问题时，他便会去找那些即便是一个业余的数学家也能有所作为的题目。他的发现非常具有挑战性，甚至可以让那些思维最严谨的人为之疯狂。吉布斯在今年年初完成的一篇论文里，对一个将面积的测量精确到原子尺度的百年难题取得了重大突破。

法国数学家亨利·勒贝格在1914年寄给好友朱利叶斯帕尔的信中首次提出这一问题。信中提到：能够完全覆盖大量其他形状（它们的直径都是1个单位长度）且面积最小的图形是什么？

在那以后的一个世纪里，勒贝格的“万有覆盖”问题便诱发出一波思潮：自从它被提出后，对于这个问题的探究呈现出令人惊讶的进步。吉布斯的改善相比之下更为可观，尽管我们仍需仔细研究才能发现。

想象一下：在你的地板上放上一打大小形状各不相同的剪纸，现在你被要求设计出另一个大小刚好，并且能够完全覆盖那些剪纸的一个形状。通过叠加和旋转这些形状，你完全可以凭感觉找到你的解决方法。但是当你找到了这个“通用”的覆盖，你如何知道他就是最小的那个呢？你可以想象出：一整天都面对着你构造出的形状，在这里或那里发现一点可以修剪的地方。

 

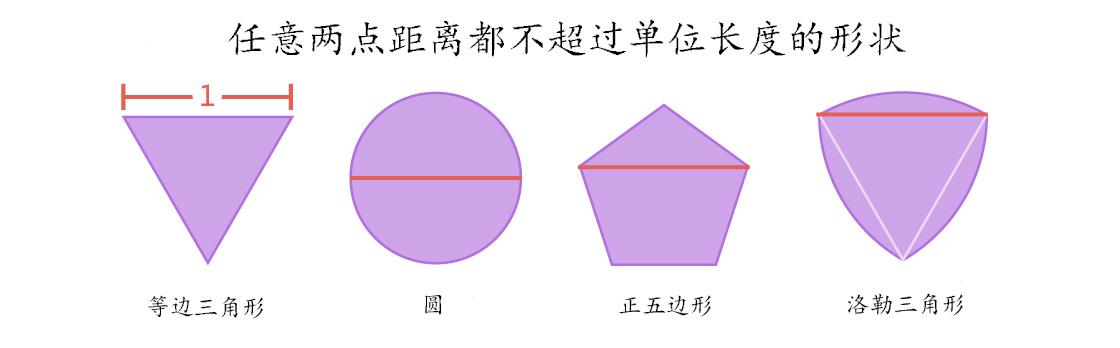
这就是勒贝格“万有覆盖空间”问题的灵魂所在，它所考虑是其内部任何两点相距都不会超过一个单位长度的形状。单位圆是最明显符合这一条件的；当然也有许多其他符合条件的形状，对于初学者来说，可以举出：等边三角形、正五边形、正六边形以及由三段弧所组成的曲边三角形（勒洛三角形）等例子。这种形状的多样性使得我们很难找到它们的最小覆盖空间。

 

 

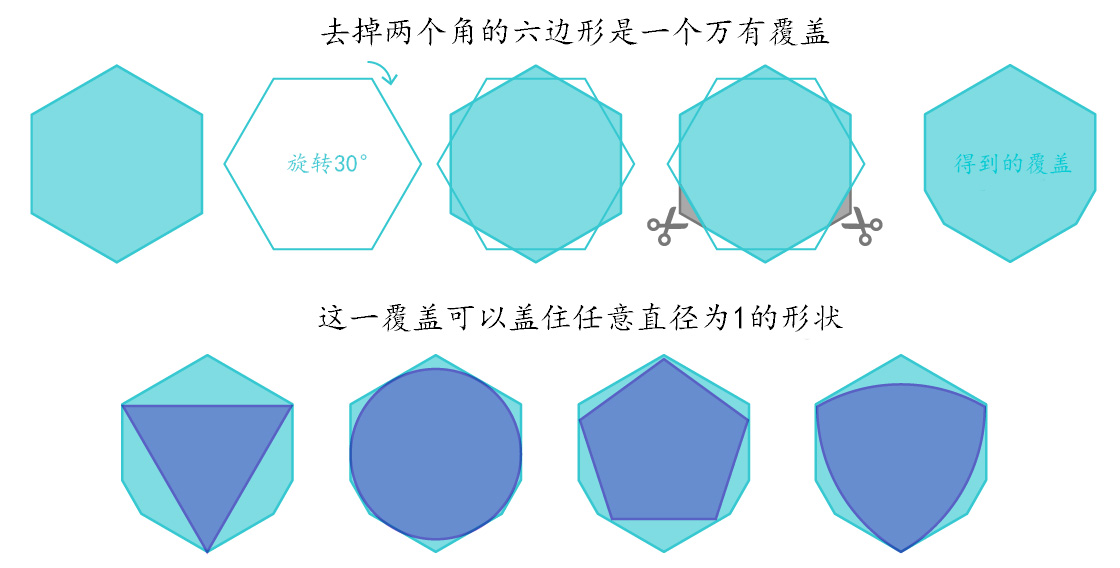
收到勒贝格的来信后不久，帕尔意识到正六边形是一个万有覆盖（边长为1/sqrt(3)，其中sqrt表示开根号）。之后他又做了一些改进，他发现当他从六边形上切下两个不连续的角所得到的形状面积更小，但仍是一个万有覆盖。

“取一个新的六边形，把它放在原来的六边形上面，将新的六边形旋转30°，这样你就能切下两个角；这就是帕尔的方案。”吉布斯说道。

在接下来的80年里，另外两位数学家在帕尔的万有覆盖上做了进一步改进：1936年罗兰·斯普拉格去掉了某个角附近的一部分；1992年汉森从右下角和左下角去掉了两个小的微乎其微的部分。汉森的面积节约方案示意图可以让我们知道它节约了哪部分，但是这难免会让我们对其节省的面积大小产生误会：他所截去的部分是0.00000000004单位面积大小。

 

.
“你不可能真的把这些碎片画出来，因为他们都是原子大小的。”约翰·贝兹，一位来自加州大学河滨分校的数学家这样说道。

2013年，贝兹在他颇受欢迎的数学博客上写了一篇关于勒贝格万有覆盖问题的文章，并在文中把这个晦涩难懂的问题表述地使人通俗易懂。他承认自己被这个问题所深深吸引，就像人们饶有兴趣地看着昆虫在水里扑腾一样。

“我对这个问题的兴趣甚至有些病态，”贝兹写到。“我不知道这个问题为何重要，我也看不出它与其他那些美妙的数学有任何联系。只是，可能和你一开始所想的相比，它似乎难得令人惊讶。我很佩服探究这一问题的人，就像我很钦佩那些决定滑雪横穿南极洲的人。”

菲利普·吉布斯从没滑雪穿越南极洲，但他读过贝兹的博客。当他看到勒贝格万有覆盖问题的帖子时，他想：“那正是我苦苦搜寻的东西。”

原子剪刀

小时候吉布斯就梦想着成为一名科学家。他在剑桥大学获得数学学士学位，并在格拉斯哥大学荣获理论物理学博士学位。然而在此后不久他便失去了学术研究的热情，转而成为了一名软件工程师。他曾从事船舶设计系统、飞机控制系统以及金融系统等，直到2006年退休。

吉布斯仍保留着对学术问题的兴趣，但作为一名非专业研究人员，他能做的屈指可数。“作为一名独立科研人员，我很难跟上当今科学发展的进度，”他说道。“但如果你找到了合适的问题，那么你就可以进行一些探究，并得出一些有用的结论。”

勒贝格的万有覆盖问题正是这样的问题，它从未引起数学家的太多关注，所以吉布斯觉得他可以在这个问题上有所作为。他也意识到可以运用自己的编程基础来增加自己的优势。“我经常寻找那些可以运用计算机来进行数学实验的问题，”他这样说道。

2004年，吉布斯对200个随机生成的直径为1的形状进行了计算机模拟，模拟的结果表明了他也许能在之前的最小覆盖面基础上再去掉顶角附近的一些区域。随后他将这个想法展开，并证明了新的覆盖对所有可能的直径为一的形状都适用。吉布斯把他的证明寄给贝兹，后者则与他的一名本科生卡琳·巴格达萨恩一起帮助吉布斯将他的论证进一步修改成更正式的数学形式。

他们三人于2015年2月将他们的论文发表在网上。文中，他们把最小万有覆盖面从0.8441377减少到0.8441153单位面积。尽管减少的部分只有0.0000224单位面积，但这却几乎是汉森在1992年减少的面积的100万倍！

吉布斯确信他可以做得更好。在十月份发布在网上的一篇论文中，他又从原有的覆盖面上剪掉了相对较大的一部分，从而把整体面积减小到0.84409359单位。

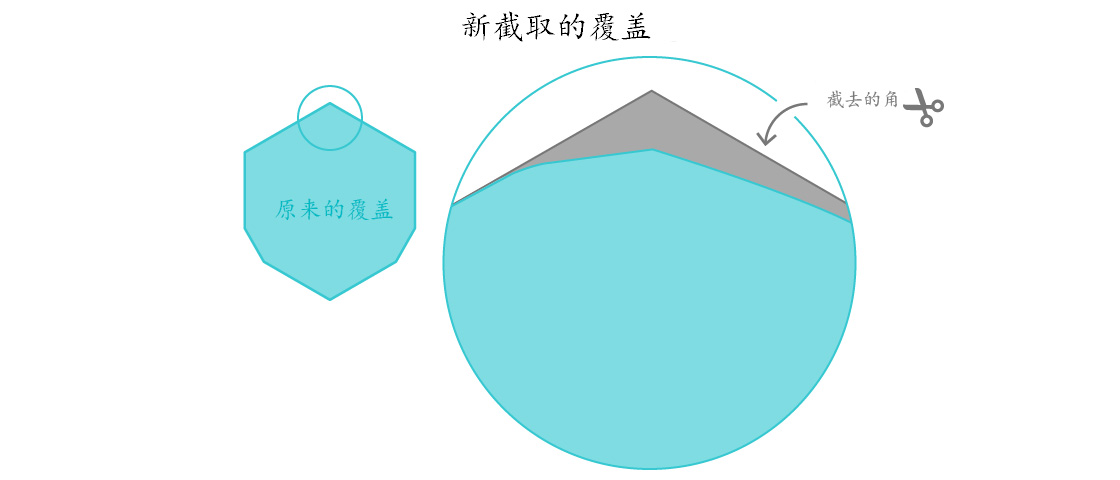
他的策略是将所有直径为1的形状移到他早些年发现的万有覆盖的某一角，然后把对角部分剩下的任何区域都去掉；然而从节省面积测量的角度来说，却是非常精确的。吉布斯所运用的技术都源于欧式几何，但为了让每个高中都能看懂，他需要确保每一步都十分精确。

“从数学角度来说，这只是高中几何难度，但是它几乎让人为之疯狂。”贝兹这样写到。

如今，吉布斯仍保有“发现最小万有覆盖”的殊荣，但是他的位置并不牢固，他相信任然有更小的万有覆盖以待我们发现。对贝兹来说，他则希望吉布斯所带来的对勒贝格这一问题的新关注能够激发其他数学家的兴趣，从而进一步完善并丰富现代数学技术。

“解决这个问题可能会涉及到非常不同的想法，”贝兹说道。“尽管我不知道这些想法具体是哪些。”

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa