你看见蝴蝶翅膀上的数学公式了吗？

 

作者，Radium，哆嗒数学网群友。

 

关注 哆嗒数学网 每天获得更多数学趣文

 

数学中最有诗意的定理莫过于蝴蝶效应了。美国气象学家洛伦兹1963年在一篇论文中分析了这个效应。最常见的阐述是“一只南美洲亚马逊河流域热带雨林中的蝴蝶，偶尔扇动几下翅膀，可以在两周以后引起美国德克萨斯州的一场龙卷风。”其原因就是蝴蝶扇动翅膀的运动，导致其身边的空气系统发生变化，并产生微弱的气流，而微弱气流的产生又会引起四周空气或其他系统产生相应的变化，由此引起一个连锁反应，最终导致其他系统的极大变化。他称混沌学。用MATLAB绘制洛伦兹模型的状态方程如下图：

 

 

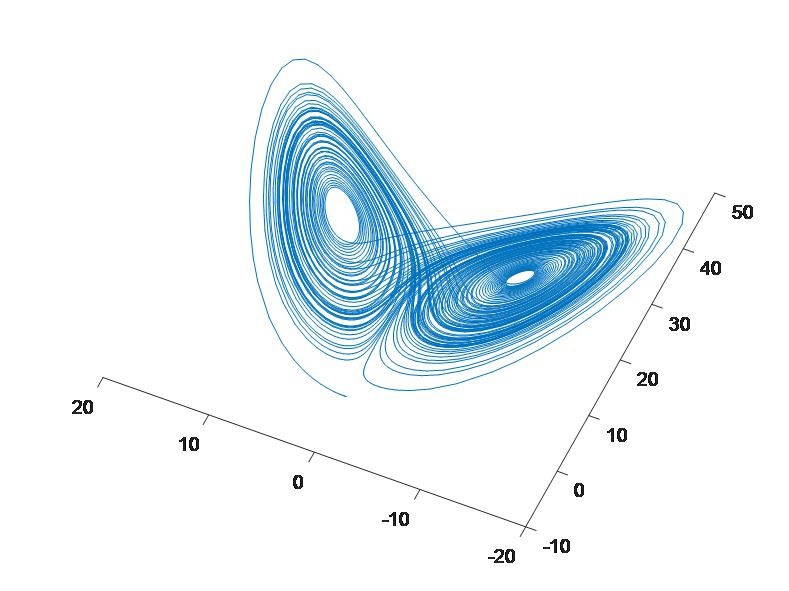
MATLAB代码：
f=@(t,x)[-8/3*x(1)+x(2)*x(3);-10*x(2)+10*x(3);-x(1)*x(2)+28*x(2)-x(3)];
t_final=100;x0=[0;0;1e-10];[t,x]=ode45(f,[0,t_final],x0);
plot3(x(:,1),x(:,2),x(:,3));
%如果欲观察相空间轨迹走行最好的方法是采用comet3()函数绘制动画式的轨迹，即将最后一条语句改为comet3(x(:,1),x(:,2),x(:,3));

可以发现图像是混沌的，而且十分像一只张开双翅的蝴蝶。因此笔者以蝴蝶为素材，从代数，分析，几何以及概率中各挑选了一个公式作为代表融合起来设计。话不多说，直接上图：

 

Cauchy-Schwarz不等式

令x,y是两个向量，则

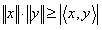
当且仅当x,y线性相关时，等式成立。

柯西不等式是由大数学家柯西(Cauchy)在研究数学分析中的“流数”问题时得到的。但从历史的角度讲，该不等式应当称为Cauchy-Buniakowsky-Schwarz不等式，因为，正是后两位数学家彼此独立地在积分学中推而广之，才将这一不等式应用到近乎完善的地步。该不等式有多种形式。

Crofton定理：

令D是平面上有界凸区域。D的两条切线通过D外每点P(x,y)。令t_1与t_2是线段长，此线段由P与切点确定，令A是各线段间的角，被看作(x,y)的函数，则

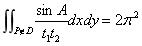
Stolz定理：

令{x_n}与{y_n}是两个实数数列，{y_n}时严格正的，递增的，无界的。若

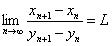
则极限

 

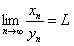
F=normcdf(x,μ,σ)

MATLAB语言，F为x各点处的正态分布的分布函数值

 

关注 哆嗒数学网 每天获得更多数学趣文