用最不专业的语言来介绍一下专业的p进数
关注 哆嗒数学网 每天获得更多数学趣文
我不是搞数论的,但我一直对p进数(p-adic numbers)有一种遥远的迷恋。我有一张关于一些我想要写一写展示在我的博客上的“简洁数学主题”的清单,p进数就在那张清单上,因此我很高兴在2008年11月的那一期的《大学数学杂志》(College Mathematics Journal)上看见了由 Andrew Rich 撰写的,标题叫做《左撇子数》的一篇有关p进数的有趣的文章。

通常的p进数的构造方法对非专业人士来说相当复杂,这里仅仅是简单地介绍它的思想。
我们从有理数开始。有理数集是能够被写成分数的数的集合。有理数的例子有4,13,2.1,22/7,0.333333…有理数中有很多的“洞”,填补这些“洞”的方法也有若干种。
从有理数走到实数——我们用通常的填补这些“洞”的思想方法创造出了实数的集合。举例来说,我们想让有理数列3,3.1,3.14,3.141,3.1415,3.14159…收敛,于是我们创造了一个叫π的新数来当做这个数列的极限点。要想理解这件事我们需要明确什么叫“逼近”,按朴素的通常理解,如果两个数数位上的数码向右数时有很长一段是一致的,那么这两个数就是“逼近”的。
如何从有理数到p进数?我们用类似的技巧来构造p进数,不同之处在于我们选择了一个新的关于“逼近”的定义。(当我们讨论p进数时,p是某个特殊的数,通常是素数,且数的数码为0,…,p-1。)现在如果两个数数位上的数码向左数时有很长一段是相同的,那么我们称这两个数是“逼近”的。于是10进数0.03,0.53,6.53,96.53,196.53,1196.53,21196.53…变得越来越靠近某个数。
通常的实数,在小数点左边只有有限位数,而在小数点右边可能有无限位数。然而,如我们所见,p进数总是可以被写成小数点右边有有有限位数,而小数点左边可能有无限多位数码的形式(这也是为什么Rich称它们为“左撇子数”)。举个例子,33.333333…不是一个10进数,但是…333333.33是。特别地,上一段落给出的数列收敛到某个10进数…21196.53。这里我们给出这种构造的一些比较酷炫的结论。
1.加法。我们可以对两个p进数相加。这里有个10进数的例子——正常相加,向左进位。(注意到加法是从右向左进行的,所以无限位p进数的加法比无限位实数的加法要容易很多。)
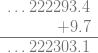
2.乘法。像加法一样,两个p进数的乘法也是可行的,而且实施起来也比实数容易很多。
3.减法。p进数里没必要为负数标记一个负号(-)。比如说,作为一个10进数,我们可以把-16写成…999984。要想证明这一点,我们只需要观察到16+(…999984)=0:
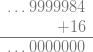
类似地,我们可以证明每个p进数都有这样一个“正相反数”,于是我们往往会把减法转化成加法来做。
4.p进有理数。每个p进有理数都可以被写成小数点右边有有限多位数码的形式。例如,我们一般会认为1/3等于0.3333…,但是在10进数中我们会把它写成…666667。要证明这一点,我们只需要观察到(…666667)*3=1:
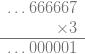
此外,Rich在文章中给了证明,一个p进数是有理数当且仅当它的小数点左边的数位上的数码向左无限循环(这与实数的情形形成一种漂亮的对称,在实数中一个数是有理数当且仅当它的小数点右边的数位上的数码向右无限循环。)
5.除法。除法会怎么样呢?Rich在文章中说明,把两个10进数相除通常可行,但不总是可以。麻烦之处在于可能有两个非零的10进数x和y满足xy=0。细节可以参见那篇文章。然而我们要重点指出,如果p是素数,那么这种情况不会发生。当p时素数时,每个非零的p进数都有一个倒数,这时我们就可以对两个这样的数做除法。
6.序关系。这是关于p进数的最后一个奇怪的事实。众所周知如果x和y是两个不相等的实数,于是要么x<y成立,要么y<x成立。但是,在p进数中没有这样的线性序关系。
7. 来点高级数学概念——数学上有更多方式来描述这些结论。如果p是素数,那么p进数形成了一个包含有理数的完备度量空间(它是有理数的完备化),且是一个域。(注意到因为除法的问题,当p不是素数时,p进数不再是域,仅仅是一个环)
要想了解更多细节,例子和证明,可以参见Andrew Rich的好文章“左撇子数”。
https://www.maa.org/publications/periodicals/college-mathematics-journal/college-mathematics-journal-november-2008
关注 哆嗒数学网 每天获得更多数学趣文

评论已关闭