“特征向量新公式”不能改变数学,但也许能改变你的解题方法
关注 哆嗒数学网 每天获得更多数学趣文
不得不说最近关于“陶哲轩的线性代数新公式”成为数学圈内最热的话题,从开始的惊诧到后面八卦娱乐,让不少人充满了欢乐。我们哆嗒数学网也发了文章,说明论文中的所谓的“新公式”并非首发。在这篇文章之前,这个公式已经不止一次出现在其他论文或者教材中了。其中目前发现最早有记载这个公式的论文在四十多年前的1968年。
这里我们希望每一个关心这件事情的人不要嘲笑当局者的任何一方,毕竟数学学科树大根深,谁也不知道从哪个犄角旮旯里出现了一个大家都不熟知的“沉睡”了许久的简单结果
。就算菲尔兹奖得主陶哲轩,也不例外,不是是什么零零碎碎的知识,他都能迅速通过肉脑搜索出来。他出现这个乌龙,一点也不奇怪。
喧嚣过后,我们哆嗒数学网的小编们突然想到,这个公式本身是真的,不是吗?再进一步思考发现,难得有菲尔兹得主发表的文章,其中的数学内容能让一个普通的大学生有可能看得懂、理解的了,说不定还能欣赏、评鉴……
——而且这还是网上热点,绝佳的一个聊聊线性代数的机会不是吗?
好了,我相信大多数关心这个新闻的人都还不知道这个公式具体是啥,因为数学家们使用的符号会让让人吓得退避三舍,不敢再深究。这篇文章将把正在读这篇文章的人看成非数学系的理工科考研党(或者相应水平),用一个简单的例子来解读这个公式到底在说啥。
首先,你都是考研党了,一定会复习线性代数这门课程的内容。知道矩阵、特征值、特征向量概念。陶哲轩的这个公式就是针对埃尔米特矩阵求特征值的公式。什么不知道什么是埃尔米特矩阵?不慌,这个类型的矩阵可能不是每一个学习线性代数的同学都会学,但是另外一个概念一定会学:实对称矩阵——矩阵里每个变量都是实数,且其转置等于本身的方阵。实对称阵是一种特殊埃尔米特矩阵,作为考研党的你,就把这个公式结果认为是针对是对称阵的,这样不会影响你品味这个公式。
好了,你理解了,这是一个可以对实对称阵求特征向量的公式。无论你大学老师还是你的考研辅导班的名师都会告诉你求方阵A特征向量的流程:
第一步:计算行列式|λI-A|=0的根,这个行列式的结果是个n阶多项式,会得到n个特征值,这里可能有重根。
第二步: 对刚才每个特征值λ,解线性方程组(λI-A)X=0,找到每个方程的线性无关的的解,得到的解就是特征值λ对应的特征向量。
这里,帮你回忆一下用到的知识点,第一步你要会求行列式、大多时候你还要分解因式来求解方程的跟。第二步,你要用到解线性方程组,有可能用到高斯消元法。
陶哲轩的那个新公式告诉你,哪怕你很菜,直到你上考场之前,都没掌握解线性方程组的方法,你一样也有可能解出特征向量,而且用到的知识点全部都在第一步当中——你只要会求特征根就行。
——少记忆一个知识点,这样讲是不是很吸引人?
这个公式会在第二步回拆成下面几个分步做:
新第二步第一分步:删掉A第1行第1列的元素,得到子矩阵,删掉A第2行第2列的元素,得到子矩阵,……,删掉A第n行第n列的元素,得到新矩阵。最后得到n个子矩阵。
新第二步第二分步:每个子矩阵计算特征值。这样每个子矩阵有n-1个特征值,这样的特征值有n组。
新第二步第三分步:通过以上不同地方计算得到的特征值,直接计算每个特征向量的分量值的绝对值。在通过线性无关的关心决定去掉绝对值的选取的符号。
陶哲轩的公式在原文里是这样的,很吓人。

于是,我们针对三阶实对称方阵来把他简化成下图这样。

我们做一道具体的题目,就算下面这道,怎么样,是不是很像你们的课后习题或者期末考试题?

这道题很容易算出x,y的值。最后就算找一个正交矩阵做对角化的问题。那个要找的矩阵P就算单位化的特征向量拼成一个矩阵而已。
特征值是,2,1,-1 ,也就是:
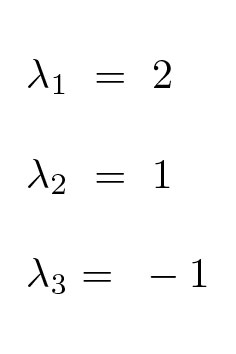
按传统做法,回去解下面的三个线性方程组,分别得到特征向量。最后得到P。

新公式的办法,会先分列子矩阵,分别计算特征值。

然后套公式解出每个分量的绝对值。
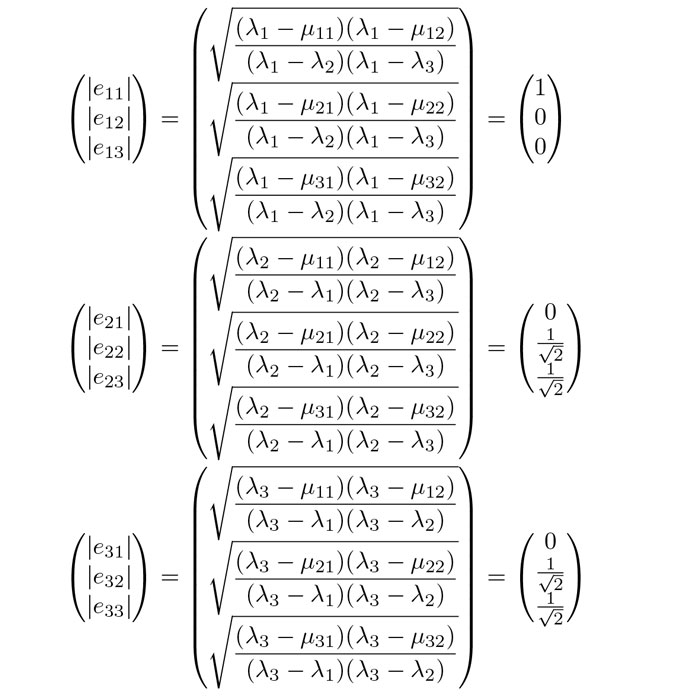
你会发现,有两个特征向量的每个分量绝对值是完全一样的,因为特征向量需要线性无关,于是很容易决定正负号的选择。另外哪个是特征值1对应的特征向量,哪个是特征值-1的特征向量还要做乘法试一试。
这样同样能得到P的结果:
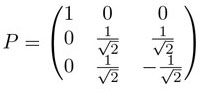
当然,我们曾经试图使用这个方法想办法解决四阶方阵的问题,一般计算量会更大,并不实用。
好了,不知道你在考试中这样做会不会得分,不过的确没有解过任何线性方程组,答案也是对的。
总之,祝你好运!
关注 哆嗒数学网 每天获得更多数学趣文

评论已关闭