三维环面：你在逃离目标，却一定回到原点

 

原文作者，Evelyn Lamb，大学数学教师

翻译作者，八，哆嗒数学网翻译组成员。

校对：Math001

 

关注 哆嗒数学网 每天获得更多数学趣文

 

在科幻剧《星际迷航：下一代》第二季剧集《沉默时刻》的剧情中，星舰企业号飞入了一个空间。为了从这个空间中出去，船员们设置了一个固定的信号标记（不用考虑这个标记在太空中静止是什么意思，或者如何将其留在太空），以便衡量他们飞了多远。当他们朝着背离信标的方向飞行的过程中，信标先是离它们越来越远，而又开始靠近，最终他们又回到了最初的地方。

 

 

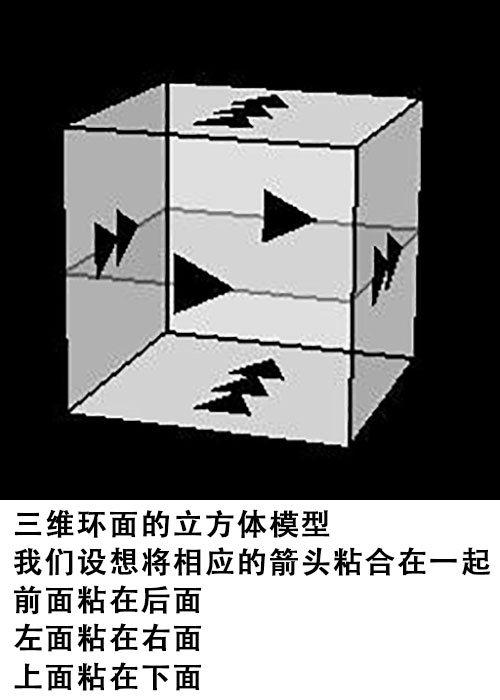
企业号并没有对这个空间做充分的探索，以至于我们无法得到确切的信息，但是他们很可能偶然间进入了三维环面（也许是纳吉卢姆那样的神族将他们了拖进去）。类似于二维环面——可以想象成一个正方形，将每一对相对的边粘合在一起——三维环面可以想象成一个立方体，将每一对相对的面粘合在一起形成的结构。想象你站在三维环面上，当你向前移动时，最终你会再次回到立方体的后方；当你向左侧移动时，最终你会再次回到立方体的右侧；当你向上移动时，最终你会再次回到立方体的底部。

 

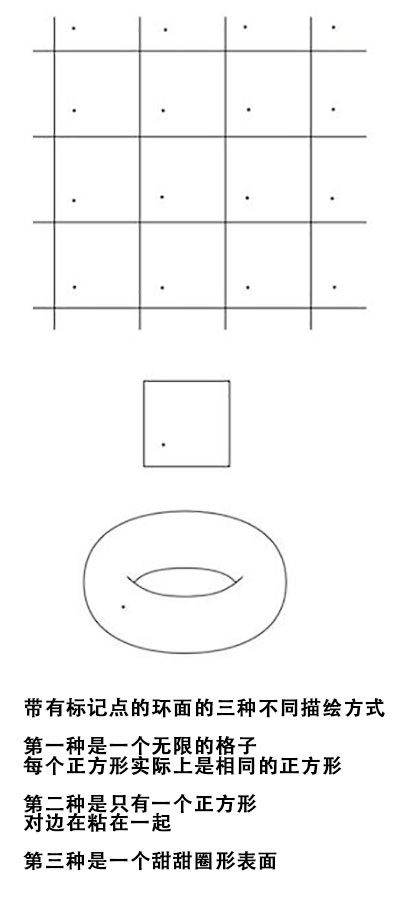
我们有很多直观的结构来想象二维环面，但很难将三维环面可视化。对于二维环面的理解，或许正方形的描述方式会有所帮助，但甜甜圈的描述方式能够让我们更加真实的体会到居住在环面上的感受。对于三维环面，我们没有足够维度来像二维环面这样来将它整体的可视化，但是我们可以尝试一下将各个面粘在一起的方式。首先，将正方体顶面粘在底面上，形成一个具有正方形横截面的实心环（大概是一个正方形的甜甜圈）；然后，我们将左侧粘到右侧，最终看起来像一个空心的甜甜圈；下一步是将内部粘合到外部，但这在三维空间不足以展示其效果。

 

 

当询问拓扑或几何学家他们的研究有什么应用时，他们往往会笼统的说用于探求宇宙的形状，然后便开始试图用庞加莱圆盘的优美图片分散别人注意力。（或者仅仅是我？）但是三维环面或许确实与宇宙的形状有关。拓扑和几何为我们提供了对所有可能的三维形状（也称为三维流形）进行分类的方法，根据宇宙已确定具有的属性，我们可以缩小宇宙可能具有的形状的选择范围。

 

我不是天体物理学家，也不了解可以帮助我们确定空间的形状的最新的测量数据，因此我也不了解当前对宇宙形状的看法。但是如果宇宙是环面呢？另一种三维环面的可视化图形向我们展示了这将是多么的怪异。

 

 

 

这种无限的支架扭曲了三维环面的一个重要特征：三维环面是有限的，而这张照片看起来是无限的。然而，这更加说明了生活在环面中会多么令人困惑。

 

 

现在，让我们收起一个维度，并考虑一下相应的二维环面。那会是平面上的无限网格，而不是仅有一个正方形。我们要记住的是，在这个平面中，任意两个位于不同正方形中处于相同相对位置的点，实际上是同一个点。

 

 

 

 

 

如果居住在环面（二维或三维）中，那么从某个角度向外看，视线可能将会环绕环面数次。

 

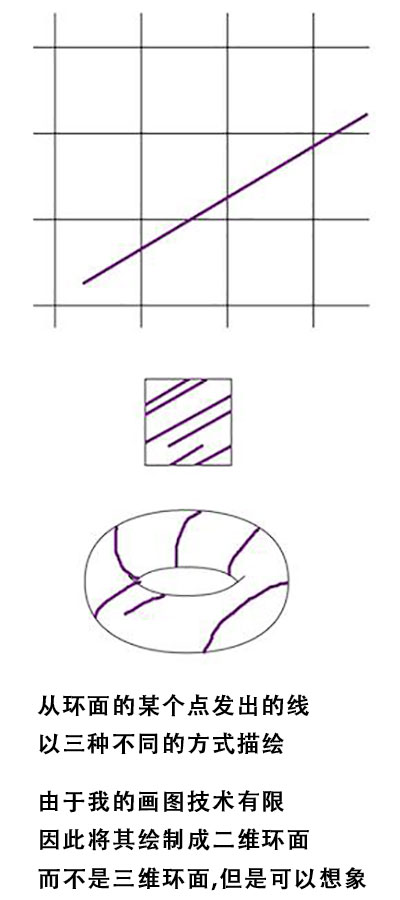
如果从三维环面中的某个点向上看，你会看到自己的脚底。只要角度和视线足够好，理论上你的视线可以无数次环绕环面。如果环顾四周，你会看到无数个自己，这一定是自恋狂的梦想。

 

 

当然，如果我们真的生活在一个三维环面中，有可能是因为空间太大才让我们看不到自己的屁股，这让我些许放心。不过，我想知道的是，我们是否能够确切的认识到我们所居住的地方到底是个什么流形。

 

 

关注 哆嗒数学网 每天获得更多数学趣文

标签: