和菲尔兹奖得主一起在微博上讨论数学作业是怎样的画风？

关注 哆嗒数学网 每天获得更多数学趣文

 

 

 

我们知道，中国人喜欢用的微博，在国外很少有人用的。他们喜欢用一个叫作推特的东西，使用方式和国内的微博差不多。

 

和国内的微博一样，大家在推特上发表的话题大部分是娱乐倾向的话题。一本正经的聊大学数学作业的就更少了 。这几天，就发生了这样有趣的一幕。

Barbara Fantechi 是意大利国际高等研究院的数学教授，其领域是代数几何。如果你百度她的名字，能搜索到她的一部著作——对格罗滕迪克名著FGA的解读。

她在推特上贴出了一个“作业题”：

假设A是一个非空集合，+是A上满足结合律和交换律的一个运算。对任意A中的元素a，A到A的映射x→x+a是双射。求证：(A,+)是一个交换群。

 

既然是大教授出的题目，看到的人即便要回复，也会给点面子吧。回答之前，都会对问题本身来个“高度评价”。 一位韩国的老师进行了回复。她首先说，这个问题对自己来说并不trivial，然后继续写出解答：

 

 

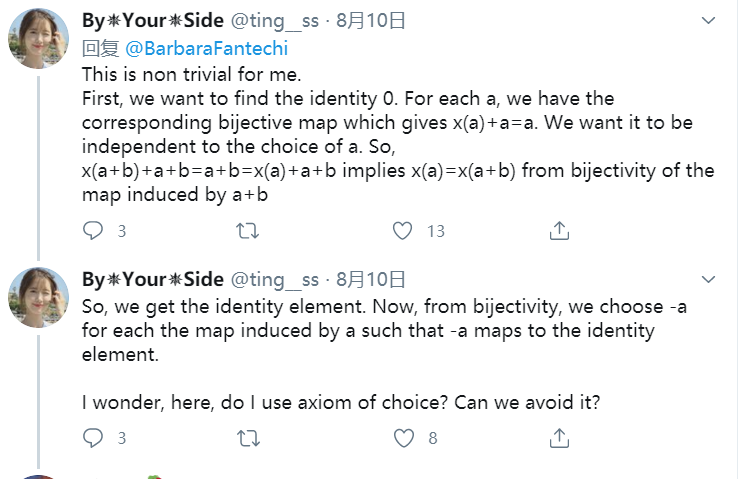
首先，我要找出单位元0。对每个a，由于双射的性质，我们能找到x(a)满足x(a)+a = a。 我想让x(a)的值和a的选取无关。用a+b诱导一个式子x(a+b)+a+b=a+b=x(a)+a+b，于是由双射的性质，则必有x(a)=x(a+b)。这样，就得到了单位元。于是，我们把-a选成由双射诱导的，与a运算后得到单位元的那个元素。最后，他还问：我想知道，我是不是用到了选择公理？能不能不用。

 

很多人回复：其实没用选择公理。

 

很多人参与的解答，方法都大同小异。连菲尔兹奖得主高尔斯也来凑热闹，在回答前，他首先说了一个“免责声明”，说自己的解答没有仔细验证过，不排除犯低级错误的可能。

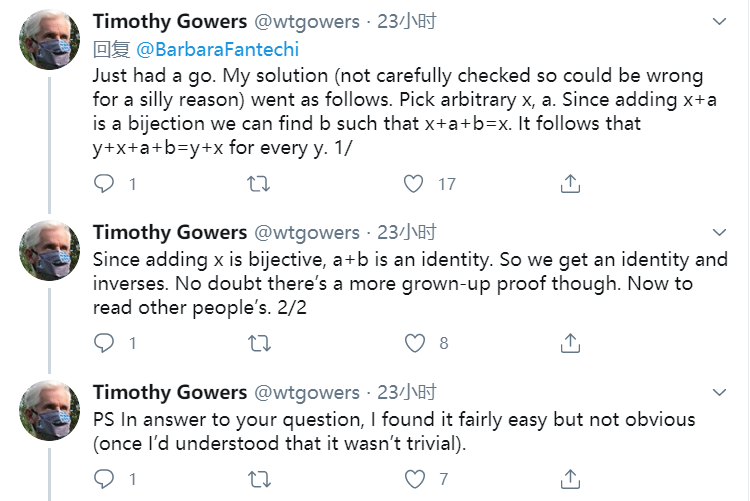
高尔斯的回答是，对任意x和a，因为加法x+a是双射，所以存在b满足 x+a+b = x。于是得到，对任意y，有 y+x+a+b =y+x。再因为双射的性质说明a+b是单位元。不排除有更高端的证明方法，我来看看别人的回复吧。——PS，这个问题非常简单，但不显然。当我明白它不平凡之后。

 

有人也玩起了花样，用上了范畴论，他这样回答的：

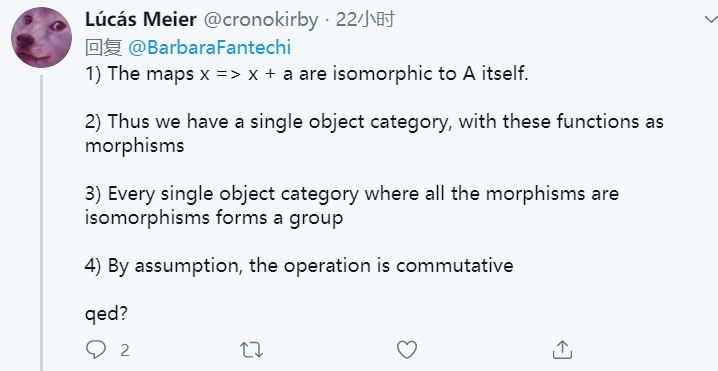
1、 映射x→x+a是集合A自身的同构

2、 因此以这些映射作为态射，构成一个单对象范畴。

3、 每个态射都是同构的单对象范畴构成一个群。

4、 根据假设，得到运算交换性。

 

回复中，有人对这个办法提出异议。说：

对于第1条，需要证明逆映射也有x+a形式。

对于第2条，需要证明恒等映射也有x+a形式。

 

还有人开始讨论，题设是否能精简。比如双射的条件能不能改成满射，而无需单射的条件。有人回复说，只是满射的话，逆的唯一性满足不了。

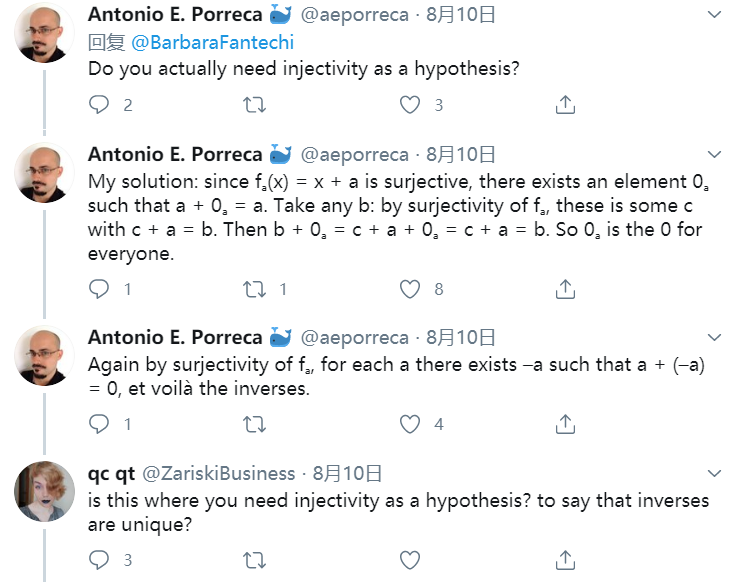
有人认为交换性的条件可以不需要。马上有人就回复了反例：如果加法定义成 x+a = x（原推应该有笔误），映射满足除了交换性的所有条件，但这个运算都不能做成一个群。

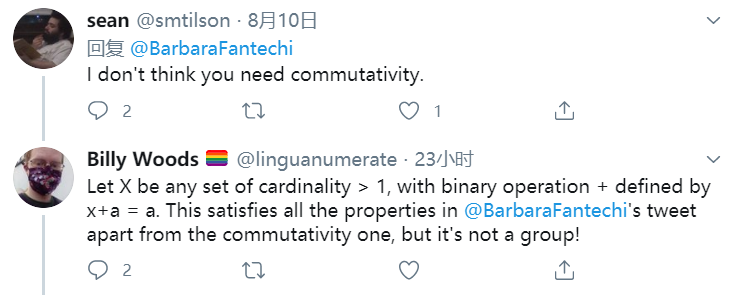
当然，还有人吐槽：你的推文让我头疼……，Fantechi教授只好回复说：Sorry。

 

关注 哆嗒数学网 每天获得更多数学趣文