希尔伯特几何公理介绍
关注微信:DuoDaaMath 每天获得更多数学趣文
作者,大漠,哆嗒数学网群友,高中生。
符号及一些说明
有三组不同的对象:点,直线,平面
点用A,B,C,D……来表示;
直线用a,b,c,d……来表示;
平面用α,β,γ,δ……来表示。
点称为直线几何的元素,点和直线称为平面几何的元素,点、直线和平面称为立体几何的元素
那么点,几何元素之间又有一定的相互关系
点A在直线a上:A∈a
点A在平面α上:A∈α
直线a在平面α上:a⊂α(直线的每一点都在平面上)
点B在点A与点C之间:B∈AC(我自己规定的符号)
线段AB与CD相等:AB=CD(原书是用≡号的,不过对于我们不常见,所以我用了=号)
∠AOB与∠COD相等:∠AOB=∠COD
等等……
(线段,角之类的能在点线面下给出定义,具体在叙述公理的时候再说)
在希尔伯特几何里面,其实点直线和平面是三个未定义的数学对象,在上面给的最基本的关系也是没有定义的,也就是说用什么来代表这些东西都是可以的,正如希尔伯特所说“我们必定可以用‘桌子、椅子、啤酒杯’来代替‘点、线、面’”。最简单的例子就是解析几何:我们定义点是实数对(x,y),定义线是{(x,y)|Ax+By+C=0},其实在这个定义下,“几何”已经失去了“直观”的形式了,因为在这个定义下的几何图形就变成了毫无几何直观的数字了,只是我们方便研究又将它画在了坐标系中而已。
我这里的关系符号∈,⊂,=并不来自于集合论,不要混淆,要再强调的是他们本身没有含义,我只是借用过来化简论述罢了。
总之,希尔伯特几何,就是将直观地几何语言(欧氏几何)抽象成了逻辑语言,我们所有的几何定理都可以用逻辑推理得到。(其实希尔伯特几何就是完备化的欧氏几何)
公理I关联公理
本组公理有八条,是前面所提的点,直线,平面这三组对象之间建立的一种联系:(为了方便论述,以后说二、三……点的,直线或平面是,都是指不同的点,直线或平面)
I1:对于两点A和B,恒有一直线a,使得A,B∈a(存在性);
I2:对于两点A和B,至多有一直线a,使得A,B∈a(唯一性);
(对于1,2,我们可以说两点确定一直线)
I3:一直线上至少有两点,至少有三点不在同一直线上;
I4:对于不在同一直线的三点A,B和C,恒有一平面α,使得A,B,C∈α;(存在性)对于任一平面α,恒有一点A,使得A∈α;
I5:对于不在同一直线的三点A,B和C,至多有一平面α,使得A,B,C∈α;(唯一性)
(对于4,5,我们可以说三点确定一平面)
I6:若A,B∈a且A,B∈α,则a⊂α;
I7:若两平面α,β有一个公共点A,则他们至少还有一个公共点B;
I8:至少有四点不在同一个平面上。
以上。
其实我想用形式语言写出来的,但是实在书上的太难翻译,而且符号难打,所以放弃了。
公理II顺序公理
本组公理有四条,规定了“在……之间”这个关系。根据这个概念,直线上的,平面上的,空间上的点才有顺序可言。
II1:对于点A,B,C,如果B∈AC,则点A,B,C是直线上不同的三点;这时,B∈CA也成立;(如图)
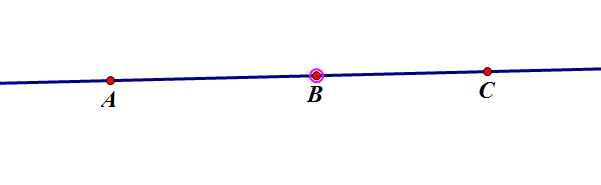
II2: 对于点A,B∈a,恒有一点C∈a,使得B∈AC;(如上图)
II3:一直线的任意三点中,至多有一点在其他两点间;
根据上面,我们就可以定义线段了:
对于直线a和直线上的两点A,B;我们把这一点对{A,B}称为线段,用AB或BA表示。在A和B之间的点叫做线段AB的点;A点和B点叫做线段AB的端点。
II4:设A,B,C是不在同一个平面的三点:对于在平面ABC且不经过点A,B,C的直线a,若a交于线段AB的一点,则它必定交于线段AC或CB的一点(如图)
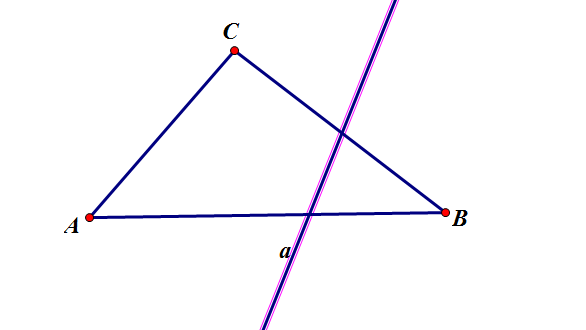
以上。
接下来定义射线

先定义同侧:设A,A’,O,B是直线a上的四点,而O在A,B之间,但不在A,A’之间,则A和A’称为在a上点O的同侧,而A,B两点称为异侧。
那么射线就定义为直线a上点O同侧的点的全体。比如与上图关于点O与B同侧的射线我们记为OB(虽然跟线段的记号一样,但注意不要混淆)
公理III合同公理
本组公理包含五条公理,主要说明几何对象“相等”的关系。
III1:对于线段AB和一点A',恒有一点B',使得线段AB与线段A'B'相等,记为 AB=A'B'
因为线段与端点的次序无关,所以一下四个等式的意义相同:
AB=A'B',AB=B'A',BA=A'B',BA=B'A'
III2:若AB=A'B'且AB=A"B",则A'B'=A"B";
(根据1,2,我们才能得到线段AB与自己相等,才能得到AB=A'B'与A^' B^'=AB等价,这并不是不证自明的事实,有了这个我们才能说两线段“互相相等”。总而言之根据1,2我们才能得到线段相等的“反身性”,“对称性”,和“传递性”,这才说明这是一个等价关系。)
III3:线段AB,BC在同一直线a上,且无公共点;线段A'B',B'C'在同一直线a'上,且也无公共点。如果AB=A'B' 且BC=B'C',则AC=A'C'
这条公理还要求线段能够相加,可以定义AB+BC=AC(其中A,B,C共线)
相当于线段一样,我们也这样来规定角相等。
我们先定义角的概念:
对于不同一直线的三点O,A,B,射线OA,和射线OB的全体我们称为角,记为∠AOB。O称为∠AOB的顶点,射线OA,和射线OB称为∠AOB的边。
同样与A,B的次序无关。
根据定义,平角,零角和凸角(大于平角的角)都不在考虑的范围内。
III4:对于∠AOB,和一条射线O'A',在射线O'A'所在的一个平面内,有且只有一条射线O'B',使得∠AOB与∠A'O'B'相等,记为∠AOB=∠A'O'B'。而且有∠AOB=∠BOA。
如同线段一样,下面四条等式的意义是一样的
∠AOB=∠A'O'B',∠AOB=∠B'O'A',∠BOA=∠A'O'B^',∠BOA=∠B'O'A'
然后先定义三角形:线段AB,BC,CA所构成的图形,记为△ABC。
III5:若△ABC与△A'B'C',有下列等式
AB=A'B',AC=A'C',∠BAC=∠B'A'C'
则有∠ABC=∠A'B'C',∠ACB=∠A'C'B'.
这条公理可以理解为三角形全等(SAS),事实上SAS这个公理的直接推论。
公理IV平行公理
这条公理显得很苍白,但在历史上很重要……
先定义平行:
对于同一平面上的两条直线线a和b,a与b无公共点,则称a与b平行,记为a∥b.
IV(欧几里得平行公理):设a是任意一条直线,A是a外的任意一点,在a和A所决定的平面上,至多有一条直线b,使得A∈b且a∥b。
根据这个公理,我们可以得到平行线内错角,同位角相等;反之也成立。
公理V连续公理
V1(阿基米德原理):对于线段AB,CD,则必定存在一个数n,使得沿着射线AB,自A作首尾相连的n个线段CD,必将越过B点。
在这里必须说下数的阿基米德原理:任意给定两个正数a,b,必存在正整数n,使na>b
V2(直线完备公理):将直线截成两段a,b(不是直线),对于任意的A∈a,B∈b,则总存在一个点C,C∈AB。
也就是说,不再存在一点不在直线上,把这点添加到直线上之后,仍满足前面的公理I~IV的
(书上的描述太笼统,我还是用我自己的话说了)
要注意的是直线完备公理是要在阿基米德原理成立下才成立的!
关注微信:DuoDaaMath 每天获得更多数学趣文

评论已关闭