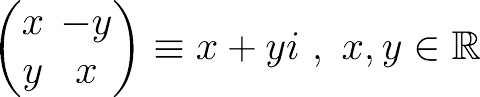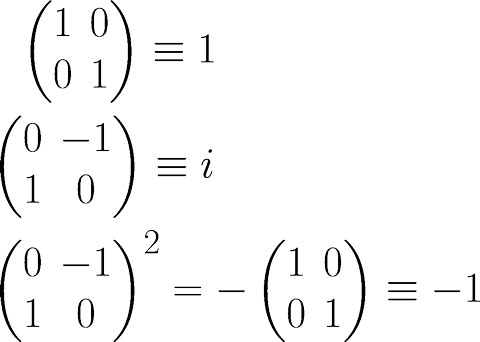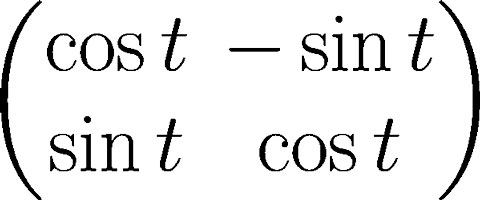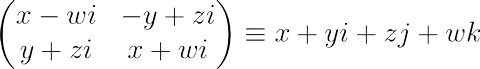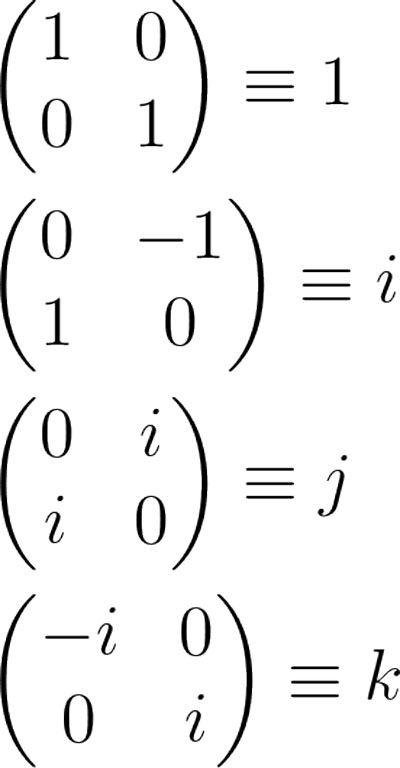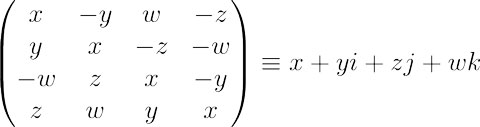关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 作者，A. R. VENKATACHALAPATHY，印度历史学家。

 译者，诗人。，哆嗒数学网翻译组成员，就读于鲁东大学数学专业。

 原文载于http://www.thehindu.com/opinion/op-ed/did-srinivasa-ramanujan-fail-in-math/article6254934.ece
 

我们的社会总离不开故事。一位数学天才竟然也有不及格的经历，这种趣事真心地让我们好奇。

拉马努金（1887-1920）是一位伟大的数学天才，但他怎么会在中期考试中不及格呢？难道是他的数学不及格嘛，还是相反考了满分？这样矛盾的观点到处都是。总有团团迷雾萦绕着天才们，让人捉摸不透，拉马努金也不例外。

有趣的是，这个谜团在这位数学家在世时就有了。1919年4月6日，正值拉马努金从剑桥回到印度之际，玛达拉斯时报发表了一篇名为“玛达拉斯的著名数学家：英国皇家学会会员，拉马努金”的人物简介。当地报纸主要从玛达拉斯港务局（拉马努金曾经在这里工作）获得关于他的一些资料，并在文中这样描写道：“在1907年12月份，拉马努金在参加他的第一文科考试（就是下文的FA）中挂掉全部科目，这显然是他的疾病拖累了他，他本人对此也只字不提。” 

斯诺是拉马努金最初赞助者，也是他的一位朋友。拉马努金的良师益友——大数学家哈代，在他精彩的回忆录《一个数学家的辩白》中评价道：“他在数学上几乎未经任何训练，拉马努金无疑是天纵之才。由于他的英语不合格，拉马努金没有成功进入玛达拉斯大学。”到这里我们就有了两个谜团：英语挂科之谜和中期考试挂科之谜。（中期课程安排在最后的大学入学考试结束之后，包括大学两年的课程，这两年结束之后，为了获得文学学士学位，还要再学习两年。中期考试又称作文科第一考试或者FA）

在同一年（1967年），阮甘纳桑，这位声名远播的“图书馆学之父”，出版了拉马努金的传记，斯诺为其作序。阮甘纳桑刚开始是一位数学教师，和拉马努金是一个时代的人。他提到在1922年，也就是拉马努金去世两年后，统计学的方法才在玛达拉斯大学作为一种光荣的数学课被首次引入。阮甘纳桑决定在一些教育问题中使用统计学方法，由于他前些年经常翻阅中期考试的书目，于是他还研究了马德里大学的标记系统。阮甘纳桑声称他在其中一卷书中发现了拉马努金的分数，“在数学考试中他真的取得了非常高的分数。他不及格完全就是因为他的其他课程太低了。这才是真实的故事。” 

罗伯特·卡尼格尔在他所著的拉马努金权威传记《知无涯者：拉马努金传》中说道，拉马努金参加了4次中期考试，统统没有通过。“除了数学，他其他的课程一塌糊涂，他参加过一个3小时的数学考试，30分钟就结束了战斗。”然格斯瓦米写了一份泰米尔语的拉马努金传记——Ragami，这本书主要参考了罗伯特·卡尼格尔对于拉马努金早年经历的记述，阮在书中说道，拉马努金参加了3次FA统统失败。另外，Ragami还添了一句，在1907年的最后一次考试中，他数学考了满分。

最近，一部基于广泛研究的文档小说《印度职员》问世，作者莱维特·戴维在这部书中强调了拉马努金的多次不及格。这个经历也被拉马努金博物馆网站反复讲述：“他悄无声息地参加FA，轻松拿到数学满分，但是在其他课程中却每次必败。”

那么对待拉马努金，我们为什么会有失败和成功这样矛盾的论断呢？正如阿希斯·南迪说道，“三人成虎，像他的数学不及格这样的流言可能会流传开来”。这两种观点都会给这位在殖民统治下成长起来的天才，蒙上一层神秘的面纱。如果他真的不及格，那么殖民主义就会饱受非议，因为它埋没了这样一位本土的天才。假如拉马努金在大学里的考试统统失败了，之后他却在国际上得到了最为崇高的认可，那么这样他的人生会显得更为戏剧与传奇。另一方面而言，拉马努金在数学考试中得到了满分，与此同时他也完败了由殖民者制定的制度。然而无论怎样，都是国家主义的造谣者占了便宜，得了好处。

虽然他远离政治，拉马努金也不得不身肩振兴忧国的重担。P.V. Seshu Iyer是当时的一位杰出的数学家，他非常欣赏拉马努金，他在1917年写道：

我们生活在一个国家巨变的时代。对于我们的力量，活力和民主，今天我们需要更多的认可。政治上我们努力争取一个团结的国家，在物质上我们渴望及早与那些发达文明国家并肩。同样在知识智力上，我们的文学和科学成就不仅没有被甩几条街，反而正在受到世界范围的认可。我们的诗人走出国门，纵声歌唱，荣耀光荣加身，骑士气质闪耀。我们的科学家们令欧美的研究院惊为天人，伟大的拉马努金先生正是在数学上，做出了这样丰功伟绩。

我们在这里发现，泰戈尔和波色（印度物理学家，物理上有玻色-爱因斯坦凝聚）曾经承担过的重担落到了拉马努金的身上。拉马努金数学挂科之谜和这种国家责任的承担有着极深的牵扯。

迷雾在或不在，问题都在那里。拉马努金真的有数学不及格吗？他到底考了多少分呢？他做的是什么试卷呢？25年前，也不知道我上辈子干了啥好事，在泰米尔纳德邦的金奈，让我三生有幸地发现了一个文件，上面有一份丢失的成绩单的备份。我将我的发现写成一篇小文章署名为“殖民教育、官僚主义与一位天才”，发表在每周政经（1988年2月13日）上。不幸的是，这个重要的发现并没有引起拉马努金研究者的关注。当时人们都爱关注拉马努金的生平和关于他的自传影片，于是我又打起精神投入研究浪潮，并把我的发现一并编入，共同呈现。

在1916年，剑桥大学正式授予拉马努金文学学士学位。天才赢得身后名，这个小小的荣誉对拉马努金来说已经显然不值一提。我们都知道在他死后，皇家协会选拉马努金为会员，剑桥大学的三一学院也认定他为成员，他也是第一个有此荣誉的印度人，那时他才年仅30岁。不过这些荣誉也引起了玛达拉斯政府的上下官员震惊，也正因如此拉马努金的成绩单才得以重见天日。

那时正是英国货物运动爆发的时期，安妮·贝赞特的家庭规则运动在印度南部兴起。短短几个月，安妮·贝赞特以监禁作为惩罚，家庭规则运动就达到了高潮。这是由一场国家主义者组织的运动，无人敢于质疑。当地日报《新印度》（1917年4月25日）以拉马努金在中期考试挂科为借口，向殖民政府发出了挑战。

“我们非常高兴地宣布：剑桥大学已经正式授予拉马努金学士学位，对此我们皆以为然，他完全配得上这个荣誉。可是假如他FA还是无法通过，那会怎么样呢（这个剑桥学位就有点说不过去了）。但那也绝不是他的错，他绝不会没有诚信。玛达拉斯大学的专家们嘲弄道，拉马努金水平就是无法通过中期考试。

这番嘲笑最终成了尖锐的讽刺。马德拉斯政府介入调查，向马德拉斯大学讯问拉马努金那份据说不及格的成绩单。弗兰西斯是那时的主管，他在他的夏季办公室里做出了回复：

办公室的记录表明，拉马努金参加了FA考试并且不及格。这是1907年的考试，也是1903年的入学考考试4年之后，经过他自己的一番学习，成绩如下：（个人信息，科目，满分，及格分数，考生分数，科目有：英语，梵语，数学，生理学，历史）

 
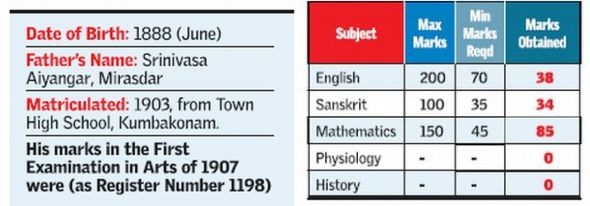
这份档案中的证据是否扫清了拉马努金挂科之谜呢？人类社会需要有趣的谜团，这样才好玩。一位数学天才在考试中挂科，可真是很赞的谈资啊！人艰不拆，说破了的人，可就输啦！

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者，大漠，哆嗒数学网群友，高中生​。

符号及一些说明

有三组不同的对象：点，直线，平面

点用A,B,C,D……来表示；

直线用a,b,c,d……来表示；

平面用α,β,γ,δ……来表示。

点称为直线几何的元素，点和直线称为平面几何的元素，点、直线和平面称为立体几何的元素

那么点，几何元素之间又有一定的相互关系

    点A在直线a上：A∈a

    点A在平面α上：A∈α

    直线a在平面α上：a⊂α（直线的每一点都在平面上）

    点B在点A与点C之间：B∈AC（我自己规定的符号）

    线段AB与CD相等：AB=CD（原书是用≡号的，不过对于我们不常见，所以我用了=号）

    ∠AOB与∠COD相等：∠AOB=∠COD

等等……

（线段，角之类的能在点线面下给出定义，具体在叙述公理的时候再说）

在希尔伯特几何里面，其实点直线和平面是三个未定义的数学对象，在上面给的最基本的关系也是没有定义的，也就是说用什么来代表这些东西都是可以的，正如希尔伯特所说“我们必定可以用‘桌子、椅子、啤酒杯’来代替‘点、线、面’”。最简单的例子就是解析几何：我们定义点是实数对(x,y)，定义线是{(x,y)|Ax+By+C=0}，其实在这个定义下，“几何”已经失去了“直观”的形式了，因为在这个定义下的几何图形就变成了毫无几何直观的数字了，只是我们方便研究又将它画在了坐标系中而已。

我这里的关系符号∈，⊂，=并不来自于集合论，不要混淆，要再强调的是他们本身没有含义，我只是借用过来化简论述罢了。

总之，希尔伯特几何，就是将直观地几何语言（欧氏几何）抽象成了逻辑语言，我们所有的几何定理都可以用逻辑推理得到。（其实希尔伯特几何就是完备化的欧氏几何）

公理I关联公理

本组公理有八条，是前面所提的点，直线，平面这三组对象之间建立的一种联系：（为了方便论述，以后说二、三……点的，直线或平面是，都是指不同的点，直线或平面）

I1：对于两点A和B，恒有一直线a，使得A,B∈a（存在性）；

I2：对于两点A和B，至多有一直线a，使得A,B∈a（唯一性）；

（对于1,2，我们可以说两点确定一直线）

I3：一直线上至少有两点，至少有三点不在同一直线上；

I4：对于不在同一直线的三点A,B和C，恒有一平面α，使得A,B,C∈α；（存在性）对于任一平面α，恒有一点A，使得A∈α；

I5：对于不在同一直线的三点A,B和C，至多有一平面α，使得A,B,C∈α；（唯一性）

（对于4,5，我们可以说三点确定一平面）

I6：若A,B∈a且A,B∈α，则a⊂α；

I7：若两平面α，β有一个公共点A，则他们至少还有一个公共点B；

I8：至少有四点不在同一个平面上。

以上。

其实我想用形式语言写出来的，但是实在书上的太难翻译，而且符号难打，所以放弃了。

公理II顺序公理

本组公理有四条，规定了“在……之间”这个关系。根据这个概念，直线上的，平面上的，空间上的点才有顺序可言。

II1：对于点A,B,C，如果B∈AC，则点A,B,C是直线上不同的三点；这时，B∈CA也成立；（如图）
 

II2: 对于点A,B∈a，恒有一点C∈a，使得B∈AC；（如上图）

II3:一直线的任意三点中，至多有一点在其他两点间；

根据上面，我们就可以定义线段了：

对于直线a和直线上的两点A,B；我们把这一点对{A,B}称为线段，用AB或BA表示。在A和B之间的点叫做线段AB的点；A点和B点叫做线段AB的端点。

II4:设A,B,C是不在同一个平面的三点：对于在平面ABC且不经过点A,B,C的直线a，若a交于线段AB的一点，则它必定交于线段AC或CB的一点（如图）

 以上。

接下来定义射线

 
先定义同侧：设A,A’,O,B是直线a上的四点，而O在A,B之间，但不在A,A’之间，则A和A’称为在a上点O的同侧，而A,B两点称为异侧。

那么射线就定义为直线a上点O同侧的点的全体。比如与上图关于点O与B同侧的射线我们记为OB（虽然跟线段的记号一样，但注意不要混淆）

公理III合同公理

本组公理包含五条公理，主要说明几何对象“相等”的关系。

III1：对于线段AB和一点A'，恒有一点B'，使得线段AB与线段A'B'相等，记为 AB=A'B'

因为线段与端点的次序无关，所以一下四个等式的意义相同：

AB=A'B'，AB=B'A'，BA=A'B'，BA=B'A'

III2：若AB=A'B'且AB=A"B"，则A'B'=A"B"；

（根据1,2，我们才能得到线段AB与自己相等，才能得到AB=A'B'与A^' B^'=AB等价，这并不是不证自明的事实，有了这个我们才能说两线段“互相相等”。总而言之根据1,2我们才能得到线段相等的“反身性”，“对称性”，和“传递性”，这才说明这是一个等价关系。）

III3：线段AB，BC在同一直线a上，且无公共点；线段A'B'，B'C'在同一直线a'上，且也无公共点。如果AB=A'B' 且BC=B'C',则AC=A'C'

这条公理还要求线段能够相加，可以定义AB+BC=AC（其中A,B,C共线）

相当于线段一样，我们也这样来规定角相等。

我们先定义角的概念：

对于不同一直线的三点O,A,B，射线OA，和射线OB的全体我们称为角，记为∠AOB。O称为∠AOB的顶点，射线OA，和射线OB称为∠AOB的边。

同样与A,B的次序无关。

根据定义，平角，零角和凸角（大于平角的角）都不在考虑的范围内。

III4：对于∠AOB，和一条射线O'A'，在射线O'A'所在的一个平面内，有且只有一条射线O'B'，使得∠AOB与∠A'O'B'相等，记为∠AOB=∠A'O'B'。而且有∠AOB=∠BOA。

如同线段一样，下面四条等式的意义是一样的

∠AOB=∠A'O'B'，∠AOB=∠B'O'A',∠BOA=∠A'O'B^',∠BOA=∠B'O'A'

然后先定义三角形：线段AB,BC,CA所构成的图形，记为△ABC。

III5：若△ABC与△A'B'C'，有下列等式

AB=A'B',AC=A'C',∠BAC=∠B'A'C'

则有∠ABC=∠A'B'C',∠ACB=∠A'C'B'.

这条公理可以理解为三角形全等（SAS），事实上SAS这个公理的直接推论。

公理IV平行公理

这条公理显得很苍白，但在历史上很重要……

先定义平行：

对于同一平面上的两条直线线a和b，a与b无公共点，则称a与b平行，记为a∥b.

IV（欧几里得平行公理）：设a是任意一条直线，A是a外的任意一点，在a和A所决定的平面上，至多有一条直线b，使得A∈b且a∥b。

根据这个公理，我们可以得到平行线内错角，同位角相等；反之也成立。

公理V连续公理

V1（阿基米德原理）：对于线段AB,CD，则必定存在一个数n，使得沿着射线AB，自A作首尾相连的n个线段CD，必将越过B点。

在这里必须说下数的阿基米德原理：任意给定两个正数a,b，必存在正整数n，使na>b

V2（直线完备公理）：将直线截成两段a,b(不是直线)，对于任意的A∈a，B∈b，则总存在一个点C，C∈AB。

也就是说，不再存在一点不在直线上，把这点添加到直线上之后，仍满足前面的公理I~IV的

（书上的描述太笼统，我还是用我自己的话说了）

要注意的是直线完备公理是要在阿基米德原理成立下才成立的！

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者,南梦玲，哆嗒数学网原创组成员，北京绳索技术协会常任理事​。

“你数学那么好，那你能证明1+1为什么等于2吗？这可是连陈景润都证明不了的！”相信各位身边有数学学霸的小伙伴们或多或少都问过其相关问题，然后就是一通争论，吵得面红耳赤最后绝招：我要和你绝交！

其实真的不需要为了这个问题就影响了好朋友的关系。好吧，我们哆嗒数学网的小编为了挽回各位小伙伴们纯洁的友谊，仔细认真的向大家介绍下1+1的故事。

陈景润老师不能证明1+1的问题，这真不是他老人家的错，这里我们不做过多介绍，只是向大家强调，我们所讨论的1加1绝不是哥德巴赫猜想，而就是讨论1+1=2的问题。

本文将从两部分介绍相关问题。

第一部分

       “上帝创造了自然数，其余的是人的工作。”——克罗内克(1823-1981)

早在远古时代，人类采集果实和打猎中产生了对计数的需求，于是使用手指、树枝、刻痕、石子等实物来进行计数。例如五个石子代表五个果实，七条划痕代表七个猎物等。这样经过较长时间，随着生产和交换的不断增多以及语言的发展，渐渐地把数从具体事物中抽象出来形成了数字，（比如古印度数字、古中亚楔形数字、古埃及数字、古玛雅数字以及现在世界通用的阿拉伯数字。（阿拉伯人是上帝？）先有数字1，以后逐次累计得到2,3,4......这样逐渐产生和形成了自然数。因此自然数也就是用来表示事物个数的存在。

而0的诞生，则代表空无一物，最初的时候，0是否为自然数颇具争议，后来国际标准ISO/IEC 80000-2规定，0属于自然数。在此我们不做讨论。

那么，很自然的，地上有1个苹果，再放上1个，就是2个苹果。这也是最早的加法的使用，纯粹的实物累计作用。这也就是为什么我们说1+1=2的最根本所在。

第一部分结束。

N年以后……

第二部分

随着时代的变迁，数学的发展，人类终于进入了新的时代不用再光着身子到处跑。我们不仅仅解决了穿衣服的问题，而且也对数的研究也有了惊人的发展，基底有了统一的规范，生活常用以十为基底的十进制计数法并且扩充数的范围到了有理数。某人被投河杀的事件也标志着无理数的诞生。公元前300年欧几里得大作《几何原本》的诞生宣告了公理化体系走进了数学领域。

​

什么是公理和定理呢？用通俗的语言说，就是人们找出一些基本的大家都认同的概念，当做不需要证明的本身就是正确的公理，（即人为规定它就是真，不服你咬我呀。有关黎曼咬欧几里得的故事请参看长篇小说《黎曼几何》）而从这一系列公理的集合，推理出的其他一些为真的命题，就是定理。

       而我们的自然数的，自然也必须将被公理化。

       1889年皮亚诺的名著《算数原理新方法》（Arithmetices principia，nova methodo exposita）出版，书中他给出了举世闻名的自然数公理。这里，我们将再次回归1+1的问题。

皮亚诺公理

         0是自然数；

         每一个确定的自然数n都有一个确定的后继，记作n'。n'也是自然数；

         如果m、n都是自然数，并且m' = n'，那么m = n；

         0不是任何自然数的后继；

         如果一些自然数的集合S具有性质：0在S中，且有，若n在S中，则n'也在S中，那么S = N。

这里我们把0当做自然数的第一个数字。（这可能和皮亚诺最开始的表述不一样。为了方便我们不去考虑0的问题）

在这里我们能看到，0是一切的开端，它不是任何自然数的后继数。那么0的后继是什么呢？总要有个符号来表示吧，那就是1；而1的后继，就是2。以此类推，我们将得到全部的自然数，用N来表示。

在这里我们再定义一下加法，也就是符号"+"的含义：

• 对于任意的自然数m有， 0+m=m  
• 对于任意的自然数m和n n'+m=(n+m)'

我们有了皮亚诺公理和+的定义，接下来就可以来证明1+1等于2了。

1+1=0'+1        (因为1是0的后续，所以第一个1用0的后续来代替)

=(0+1)'          (根据加法定义II）

=1'             (根据加法定义I)

=2              (1的后续用符号表示就是2)

到此我们便在皮亚诺公理体系之上，证明了1+1=2这个定理。

到此告一段落。不知小伙伴们纯洁的友谊是否得到了弥补？在此笔者祝愿大家永远不要忘记，争论这些本源问题时，我们所抱有的求知欲望。

其实关于自然数的皮亚诺公理还有很多故事可讲，比如Hatcher从一些基础系统，包括ZFC和范畴论推导出了皮亚诺公理。他也从弗雷格的Grundgesetze系统出发，使用现代符号和自然演绎谨慎的推导出这些公理，虽然罗素悖论曾经让其很悲剧，但George Boolos和Anderson与Zalta等人对它进行了修补，这就又是另外的传奇故事了。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文地址：http://www.eurekalert.org/pub_releases/2015-08/afps-pma081015.php

译者,智轮居士，哆嗒数学网翻译组成员。

如果你一想起数学考试就冷汗直流，你的爸爸妈妈或许应该负一定的责任。——来自《心理科学》杂志上发表的一项最新调查研究。

一个由芝加哥大学的心理学家席安·贝洛克和苏珊莱文带领的研究团队发现，如果孩子的父母有“数学焦虑症”，那么他们在校期间会花费更少的时间学数学，从而更加容易成为“数学焦虑症”患者。如果这样的父母还经常辅导孩子的数学作业的话，问题会更严重。

这篇文章的主要作者艾琳A.马洛尼是一名芝加哥大学的心理学博士后学者。杰勒德拉米雷斯和伊丽莎白·冈德森跟高级作者莱文和贝洛克共同撰写的这篇文章。

这个团队之前的一次研究已经证实了如果教师对数学有焦虑感，则学生在校期间会花费更少的精力去学数学。最新的研究则是针对数学焦虑感，将孩子与父母之间建立起某种联系。这些发现表明，成年人对待的数学的态度会对孩子的数学成绩产生重要影响。

“我们经常不去思考父母自身的态度在决定孩子的学术成就时起到多么大的作用。但是我们的实践表明，当父母漫不经心的走来走去并说诸如“哦，我不喜欢数学”或者是“这些东西让我感到压抑”，孩子们在不经意间记住这些信息，这些信息会对他们的成功构成潜移默化的影响。”心理学专家贝洛克解释道。

“数学焦虑症父母或许在给孩子们解释数学概念的时候非常没有效率，对于孩子在解决数学问题遇到的错误或者是新颖方法时反应不是很恰当。”心理学教授莱文补充道。

来自438个家庭的孩子和家长参与了这项研究，孩子都是小学一、二年级学生。学年开始时，研究者们记录了每个孩子的数学能力和“数学焦虑”程度(math anxiety)，学年结束时，又重测了一遍这些指标；此外，研究者们还记录了孩子的阅读能力，作为对照指标(父母的“数学焦虑”不影响子女阅读能力的发展)。

同时，这些孩子的父母需要完成一份问卷，这份问卷测量了父母的“数学焦虑”程度，以及父母辅导孩子数学功课的频率。（大家也来试试问卷？——哆嗒数学网注）

调查者们认为父母的数学焦虑感与孩子们数学方面的表现之间的联系，更多的归因于对待数学的态度而不是遗传基因。

“尽管在数学焦虑方面确实有基因的成分在里面,”调查者们写道，“父母的数学焦虑感只有在他们频繁的辅导孩子数学功课的时候才会把这种焦虑感传染到孩子身上。父母在辅导子女数学课业时表现出来的，对数学的畏惧态度，才是真正的元凶。未来工作不仅应该关注如何降低父母的‘数学焦虑感’，还应该关注如何提高父母辅导功课的技巧。”

马罗尼表示，这项研究说明了父母在辅导孩子功课之前，应该做更多的准备。“我们不能仅仅告诉父母--尤其是那些对数学感到焦虑的”。马罗尼解释道，“我们需要建立更好的工具去引导父母如何更加高效的辅导孩子的数学功课。”

“这些工具或许包含数学书，电脑以及传统的棋盘桌游，或者互联网应用程序，它们能够使父母与孩子在处理数学问题时进行积极地互动。”调查者们写道。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者：小米，哆嗒数学网群友，就读于纽约大学柯朗研究所。

大家打扑克牌时，洗牌一定是一项必备技能。对切法是一种常用的洗牌方法，主要流程是先将牌分成两半，以姆指扣紧牌，使牌弯曲，姆指逐渐松开内向拨牌，使兩叠牌交錯叠在一起（注1）。

今天我们就要问一个数学上的问题：用对切法要洗多少次牌才能把一副牌洗均匀呢？

回答这个问题分为两部分：第一部分是给出对切法洗牌的数学描述，第二部分是给出“洗均匀“的数学定义。为了讨论方便，我们假设一副牌有n张牌，而把我们的结果用到现实中时，n=54。

我们先把对切法洗牌过程数学化。

假设我们把一副扑克牌牌面朝下放置。

对切法洗牌分为两步：

第一步我们需要把牌分成两堆，第二步是把两堆牌按某种方式混合在一起。

现在我们在第一步中的两堆牌分别称为“上牌堆”和“下牌堆”，并把上牌堆中的牌标记为1，下牌堆中的牌标记为0。

设上牌堆里有k张牌，也就是说有k张牌被标记了1，(n-k)张牌被标记为0。这样，当我们完成一次洗牌后，从上往下观察牌堆，将会看到一个0和1组成、长度为n的序列，其中恰好有k个1和(n-k)个0。

我们可以把上面的过程逆过来，称之为一次“逆洗牌”。

一次逆洗牌对应着顺序相反的两步：

第一步，给牌堆中的每张牌标记上0或1；

第二步，把标记为1的牌从牌堆中抽出，并保持原来的相对顺序整体叠放在标记为0的牌的上方。

因此，每一种对切法洗牌（由上牌堆数目之多少，以及以何种方式混合两堆牌决定），与一个长度为n的0、1序列一一对应。

下面我们给出一个理想化的对切法洗牌，其对应的长度为n的0、1序列是随机生成的。也就是说，在逆洗牌的第一步中，对牌堆中的每张牌，我们以1/2的概率标记为1，以1/2的概率标记为0。

这种洗牌方式又称作GSR（Gilbert-Shannon-Reeds）洗牌法。一次GSR洗牌是一种特殊的对切法洗牌。

在第一步中，上牌堆的牌数为k的概率是C(n,k)/2^n（注2），这恰好是给n个数随机赋值0和1，恰好有k个1和(n-k)个0的概率。

根据概率中的中心极限定理，k大概服从N(n/2,n)，即均值为n/2，方差为根号n的正态分布；也可以说，几乎就是平均地把牌分成两堆。

在第二步的混合中，我们在牌堆的n个位置中随机选取k个位置，然后把上牌堆的牌保持原来的顺序放入这k个位置中；然后再把下牌堆的牌保持原来的顺序放入余下(n-k)个位置中。可以说，GSR洗牌既很好地模拟了实际情况，数学上又十分简单。

进一步，我们可以考虑连续m次GSR洗牌的逆过程。

我们把m次GSR洗牌前扑克牌的顺序称作“初始牌序”，把m次GSR洗牌后的顺序称为“最终牌序”。那么连续m次GSR洗牌的逆过程，就是从一个最终牌序还原出初始牌序的过程。

那么m次GSR洗牌的逆过程是怎样的呢？

经过简单的思考，我们发现我们需要对每一张牌随机指定一个长度为m的0、1数组，数组的第一个0或1表示这张牌在第一次洗牌时这张牌来自于上牌堆还是下牌堆，第二个0或1则表示第二次洗牌时这张牌来自上牌堆还是下牌堆，以此类推。

我们举一个例子，假设有5张牌，2次GSR洗牌后得到的最终牌序是DBACE，现在我们给每张牌指定一个长度为2的0、1数组如下

D: (0,1)

B: (1,0)

A: (1,1)

C: (1,0)

E: (0,0)

当然，如果指定的0、1数组不一样，还原出来的初始牌序也不同。让我们先看看对于上述的0、1数组，初始牌序是怎样的。

第1次逆洗牌我们需要看这5个数组的第2个分量，它们表征每张牌在第1次逆洗牌中（对应着第2次洗牌）被分到上牌堆还是下牌堆。由于AD的第2分量为1，BCE的第2分量为0，所以进行第一次逆洗牌后，我们得到DABCE。

第2次逆洗牌我们需要看数组的第1分量，由于ABC的第一分量为1，DE的第1分量为0，所以我们应当把ABC移到前面，得到ABCDE。（当然啦，这个例子是经过设计的，不然也不会这样巧得到ABCDE。）

当我们再仔细思考这个过程，发现m次逆洗牌可以一次性完成！

如果我们把一个长度为m的0、1数组通过二进制对应一个0~(2^m-1)整数，如下

D: (0,1)  --> 0*2 + 1 = 1

B: (1,0)  --> 1*2 + 0 = 2

A: (1,1)  --> 1*2 + 1 = 3

C: (1,0)  --> 1*2 + 0 = 2

E: (0,0)  --> 0*2 + 0 = 0

那么我们可以这样一步到位完成m次逆洗牌：先把最大的整数3对应的A称到最前面，再把整数2对应的BC紧接着A后面（这时有两个字母B和C对应着相同的整数2，必须保持B和C在最终牌序DBACE中的相对顺序），然后把整数1对应的D移到ABC后面，最后把0对应的字母E移到ABCD后面。瞧，我们又得到了ABCDE！

一般的来说，一次性完成m次逆洗牌分为两步。

第一步，“指定数字”：每张牌随机指定一个0~(2^m-1)中的整数。

第二步，“重新排序”：按每张牌被指定的数字大小，从大到小重新排列所有的牌；如果出现多张牌被指定的数字一样，那么在排列时必须保持原来的顺序。

值得指出的是，m次GSR洗牌与m次逆洗牌有一一对应关系，也和n张牌被指定0~(2^m-1)中整数的不同方式一一对应。由乘法原理，一共有2^nm种指定整数的方法，因此也有2^nm种完成m次GSR洗牌的方法，同时，这2^nm种方法都是等可能的，概率为1/2^nm。另一方面，对于同样的初始牌序和最终牌序，也有可能对应着多种洗牌方法。

完美解决了第一个问题后，接下来我们得弄清楚，究竟怎样才算是“洗均匀”呢？

我们先感性地认识一下这个问题。

在一次性完成m次逆洗牌的过程中，我们看到当有两张以上的牌被指定了同样的整数时，它们在初始牌序和最终牌序中的相对顺序会完全一样。而我们也看到，当m足够大时，为n张牌指定的n个0~(2^m-1)中的整数很可能两两不一样，这样，初始牌序和最终牌序就完全无关了。因此，一个合理的洗牌次数m，应该使得有一定的概率（例如25%）能够使n张牌被指定的整数完全不一样。

在数学上有，这样一个生日问题与此非常类似。假设一个班上有N个人（如N=30），假设每个人的生日都是独立的，问任意两个人的生日都不相同的概率有多大？

我们可以这样考虑这个问题。给N个人编号1，2，...，N。

第1个人的生日可以随便选取；第2个人的生日为了避开第1个的生日，只能从剩下的364天中选择；第3个人的生日为了避开前2个人的生日，只能从剩下的363天选择...

最终根据乘法原理，N个人的生日全部不相同的概率由(1-1/365)(1-2/365)...(1-(N-1)/365) 给出，当N不太大时，约等于(1-1/365)^N。

回到我们的洗牌问题。我们需要为n张牌中的每张牌指定一个0~(2^m-1)中的整数。那么所有被指定的整数都不一样的概率有多大呢？这时“生日”数相于2^m；而N相当于总的牌数n。根据前面的公式，n个“生日”全部不等的概率约等于(1-1/2^m)^n。

根据微积分中的重要极限 (1-1/x)^x=1/e，x→∞，我们得知，为了使(1-1/2^m)^n不是一个太小的数（在数量级的意义上，例如我们可以认为0.01是比较小的数，而0.1是相对比较大的数），必定有2^m和n差不多大。这样我们得到了第一个估计：2^m > n，也就是m>log_2 n。

在n=54时，log_2(n)大概是5.5。至少我们的感性认识给出了洗牌次数的正确的数量级！

为了更精确地给出数学上“洗均匀”的定义，我们引入两个概率分布的距离的概念。

对于两个概率p和q，对应的分布列分别是(p1,p2,...,pN)和(q1,q2,...,qN)，那么我们定义它们之前的（全变差）距离为d(p,q)=|p1-q1|+|p2-q2|+...+|pN-qN|。

这怎么应用到我们的洗牌问题上呢？

首先，不妨总是假设我们给n张牌编号为1,2,3,...,n，并且初始牌序就是1,2,...,n。最终牌序则由一个{1,2,...,n}到{1,2,...,n}的双射h给出：

对于编号为i的牌，经过m次GSR洗牌后，它的位置变成了第h(i)张牌。我们常常也以同样的字母h表示一个最终排序。

我们知道n张牌一共有N=n!种排序方式。通过m次GSR洗牌，h显然就是这N种排序方式的其中一种。事实上，h以一定的概率得到给定的一个排序方式，这其实是对应了一个分布列(p1,p2,...,pN)，表示h取每种排序方式的概率。另一方面，我们可以考虑另一个分布列(1/n!, 1/n!, ..., 1/n!)，这表示每种排序都以相同的概率1/n!出现。

显然，我们可以定义把“洗均匀”定义成两个概率分布p和q的距离d(p,q)足够小（这里的“足够小”可以理解为，如小于1/2）。

接下来，我们的问题就转化为，对于一个给定的最终牌序h，从1,2,...n的初始牌序出发，通过m次GSR洗牌，得到h作为最终牌序的概率（记为p(h)）有多大。

由于m次GSR洗牌的2^nm种洗牌方式都有相等的概率1/2^nm，我们只需要计算有多少种GSR洗牌方式，能从1,2,...n得到h。等价的，我们只需要计算有多少种逆洗牌方式，能从h得到1,2,...,n。

现在我们用f(i)表示编号为i的牌，在逆洗牌的第一步“指定数字”中，被指定的0~(2^m-1)中的整数。f可以看作一个从{1,2,...,n}到{0,1,2,...,2^m-1}的函数。

现在我们的问题是，对于给定的最终牌序h，有多少个f能把h通过m次逆洗牌变成1,2,...,n呢？

我们还是先考虑怎样从DBACE通过2次逆洗牌得到ABCDE。

为了得到ABCDE，显然我们要有f(A)>= f(B) >= f(C) >= f(D) >= f(E)，也就是说f是一个减函数。

其次，由于在最终牌序中，A在B之后，所以f(A)不能等于f(B)，因此f(A)>f(B)；同理，C在D之后，我们也必须有f(C)>f(D)。可以验证，只要f满足f(A) > f(B) >= f(C) > f(D)>= f(E)，我们都可以从DBACE通过2次逆洗牌得到ABCDE。

现在问题就转化为，求所有函数{1,2,3,4,5}到{0,1,2,3}的函数f（我们把A和1等同，B和2等同，以此类推），使得f是减函数，并且在f(1)和f(2)、f(3)和f(4)之间的严格减函数。事实上，我们可以把f稍加变形，变成一个严格减函数。

令g(1)=f(1)+2, g(2)=f(2)+2, g(3) = f(3)+1, g(4)=f(4)+1, g(5)=f(5)，那么g是一个从{1,2,3,4,5}到

{0,1,2,3,4,5}的严格减函数，并且每一个这样的g和我们要求的f一一对应。显然，这样的函数g的个数与在{0,1,2,3,4,5}中选取5个不相等的整数的方法数一样，用组合数给出就是C(6,5)=6。

我们把上面的情况推广到一般的n和最终牌序h。首先f必须是一个减函数。如果h(i)>h(i+1)，也就是说标号为i的牌在最终牌序中位于标号为i+1的牌之后，那么f(i)必须严格地大于f(i+1)，即f(i)>f(i+1)。

现在我们定义h对应的“逆序量”R=R(h)为所有满足h(i)>h(i+1)的i的个数。那么满足条件的函数f的个数，与所有从{1,2,...,n}到{0,1,..., 2^m-1+R}的严格减函数g的个数相等，进一步地，与{0,1,...,2^m-1+R}中选取n个不同整数的方法数相等。因此，满足条件的f一共有C(2^m+R, n)个。

于是，得到最终牌序h的概率为

这里我们用到了一个近似：当x1,...,xk很小时，(1+x1)...(1+xk)约等于1+x1+...+xk。

进一步我们得到全变差距离为

上面和式中的最后一项，正好是当h等概率地从n!种所有可能排序中随机选取时，其对应的逆序量与n/2偏差的期望。

更进一步的分析其实可以得出，R(h)几乎服从N(n/2,n)，即均值为n/2，方差为根号n的正态分布。因此逆序量与n/2偏差的期望约等于根号n。这样我们得到d(p,q)约等于n^(3/2)/2^m。

由n^(3/2)/2^m < 1/2我们得到m> 3/2* log_2(n) +1。当n=54时，这个数字大约是9.6。

当然啦，有一种说法是洗牌洗7次，洗7次牌也仅仅是个约数罢了，也许就是叫得比较顺口吧。通过不同的计算表明，洗牌少则5、6次，多则9、10次，就能把牌洗得很均匀了。同时我们的计算还表明，洗牌次数只取决于n的对数。也就是说洗2副牌，也只需要比洗一副牌多一两次足矣！

注1：描述来自维基百科https://zh.wikipedia.org/wiki/%E6%B4%97%E7%89%8C

注2 :C(n,k) = n!/k!(n-k)!为组合数。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者：逆蝶，哆嗒数学网群友

虚数，是数系中最伟大的发现之一，但是就像无理数的发现过程是坎坷的一样，引入虚数的路途也不是一帆风顺的。在虚数刚出现之时，曾引起数学界的一片困惑，认为虚数是没有意义的，想象的，虚无缥缈的，很多大数学家都不承认虚数。

莱布尼茨曾说：“虚数是神灵遁迹的精微而奇异的隐蔽所，它大概是存在和虚妄两界中的两栖物。”

然而虚数并不是偶然引入的一种虚无缥缈的东西。三次方程求根问题是历史上一个著名的数学问题，一直有数学家尝试给出这个问题的解。直到十六世纪，意大利数学家塔塔里亚才发现三次方程的求根公式。在这之后，虚数的引入就成了一个实际的数学问题，而不再是单纯的一个符号演算。不承认虚数的存在，就意味着无法求解三次方程的根。

虚数出现之后，法国数学家棣莫佛发现著名的棣莫佛公式，欧拉用i表示-1的平方根，将i作为虚数的单位，挪威测量学家韦塞尔试图给虚数以直观的几何解释，高斯对于复素数进行了一系列的研究。再加上柯西及阿贝尔的努力，以及复变函数论的创立，复数理论才比较完整和系统地建立起来，逐渐为数学家所接受。

复数z被定义为二元有序实数对(x,y)，记为z=x+yi，其中i是虚根单位。在复数z=x+yi中，x=Re(z)称为实部，y=Im(z)称为虚部。当虚部b=0时，z可视为实数；当虚部b≠0而实部a=0时，z称为虚数，或者纯虚数。

定义两虚数a+bi与c+di的加法：(a+bi)+(c+di)=(a+c)+(b+d)i

乘法：(a+bi)(c+di)=(ac-bd)+(bc+ad)i

根据乘法的定义可得i²=-1，容易验证复数运算和实数运算的运算法则基本相同，只不过是在运算过程中带上符号i而已。

将复数z=x+yi等同于平面上的点或者向量(x，y)，那么z有长度sqrt{x²+y²}(这里sqrt表示开根号)，称为复数z的模长，记为|z|。复数z'=x-yi，即z关于x轴的对称点，称为z的共轭复数，容易验证zz'=|z|²。另外复数的加法，就等同于向量之间的加法。

记r=|z|，t为z与x轴正方向的夹角，称为z的幅角，那么有x=rcost，y=rsint，于是有z=r(cost+isint)，称为复数z的三角表示。欧拉证明了e^(it)=cost+isint，所以也有z=re^(it)(x^y 表示x的y次方)，称为z的指数表示。

复数的乘法用三角表示或者指数表示是简单的。通过三角函数的运算可以简单证明若z=re^(it)，w=pe^(is)，那么zw=rpe^(i(t+s))。也就是说，两个复数相乘所得到的复数，其模是两个复数模的乘积，其幅角是两个复数幅角的和。因此w乘以z，即为w的长度伸缩为原来的r倍，并将w逆时针旋转角度t。

利用e^(πi/2)=cos(π/2) + i sin(π/2)=i，可得一个复数z乘以i所得复数iz可以由复数z逆时针旋转90°得到，这说明复数的确是有几何意义的。

除了以上的几种表示，复数还有矩阵表示。把复数z=x+yi等同于下面形式的矩阵。

那么容易验证复数的加法与矩阵的加法相容，复数的乘法也与矩阵的乘法相容，而且令人惊奇的是这样的矩阵在矩阵乘法下居然是可以交换的。而复数的模长即为矩阵行列式的平方根，复数的共轭就是矩阵的转置。并且还可以发现下面图片所展示的等同关系。

当r=1，即z=e^(it)时，z乘以一个复数w相当于把w逆时针旋转角度t。根据同种理由，称z所对应的矩阵（如下图）为旋转矩阵。

关于复数的减法，自然的定义为(a+bi)-(c+di)=(a-c)+(b-d)i。对于除法，由zz'=|z|²，可以得到1/z=z'/|z|²，这提醒我们可以把复数除法定义为w/z=wz'/|z|²。

这样所有的复数就够成了一个域，称为复数域，复数域是对实数域的扩充。复数域是实数域的代数闭包，也就是说任意的复系数多项式在复数域中总有根，这称为代数基本定理。n次多项式总有根的第一个正确证明是高斯在1799年的博士论文中给出的。

这里对高斯整数做一个简单介绍。每个形如m+ni的复数称为高斯整数，其中m，n是整数。类似于素数，如果m+ni=(a+bi)(c+di)可以得到a+bi或者c+di等于1，-1，i，-i中的某一个数，那么称m+ni是复素数或者高斯素数。显然的关系式5=(1+2i)(1-2i)，说明素数5不是复素数，所以素数并不一定都是复素数。确定一个复整数是不是一个复素数，比确定一个整数是不是素数更为困难。另外类似于整数的算数基本定理，复整数也可以表示成复素数的幂相乘。

从实数系到复数系扩充的成功，促使许多数学家考虑复数系的扩充，一般称之为超复数，其中最成功的人物是哈密顿。

哈密顿澄清了复数的概念，这使他能更清楚的思考超复数的问题。他先是寻找三维或三分量的数，并要求具有实数和复数的若干性质。经过若干年的努力之后，哈密顿被迫做出两个让步，一是他所作的新数包含四个分量，二是他放弃了乘法交换律。他称得到的新的数系为四元数，而三元数的不可能性到后来才被人们意识到。

四元数是简单的超复数。复数是由实数加上虚数单位i组成，其中i²=-1。哈密顿考虑复数系的扩充，另外引入两个虚根单位j，k，并有i²=j²=k²=-1。

四元数q被定义为四元有序实数组(x,y,z,w)，记为q=x+yi+zj+wk。两个四元数的加法与复数的加法类似，为对应坐标相加。若p=a+bi+cj+dk，q=x+yi+zj+wk，那么p+q=(a+x)+(b+y)i+(c+z)j+(d+w)k。

为了定义两个四元数的乘法，另外规定：ij=k，jk=i，ki=j，这与三维空间向量的外积颇有类似之处。因为ik=i(ij)=i²j=-j，所以根据之前的关系式可以类似得到：ji=-ij=-k，kj=-jk=-i，ik=-ki=-j。

因为ij≠ji，所以乘法不满足交换律。另外由于将i,j,k轮换之后，i,j,k的运算关系式不变，这说明i,j,k的位置是等价的，并没有哪个虚根单位比另一个更特殊，例如完全可以把四元数q写为q=x+zj+wk+xi，从而把z放在第二个坐标。

与复数类似，将q等同于四维空间中的点或向量(x,y,w,k)，那么q有长度sqrt{x²+y²+z²+w²}，称为四元数q的模长，记为|q|。四元数q'=x-yi-zj-wk，即q关于x轴的对称点，称为q的共轭四元数，容易验证qq'=|q|²。另外四元数的加法，就等同于四维向量之间的加法。

四元数不像复数那样有很好的三角表示，也没有好的指数表示，只有方向余弦q=r(cosα+icosβ+jcosγ+kcosθ)这种较为复杂的三角表示，其中α，β，γ，θ是q与四个坐标系的夹角，r=|q|为q的模长，但是这种表示并不能像复数的三角表示那样可以简化四元数乘法的运算。另外虚根单位i,j,k也可以理解为四维空间的旋转，但是其意义与复数旋转的意义相比较为复杂的多。

四元数有两种矩阵表示。

第一种是复矩阵表示，把q=x+yi+zj+wk等同于下面的矩阵。

那么四元数的加法与矩阵的加法相容，四元数的乘法也与矩阵的乘法相容，而四元数的模长为矩阵行列式的平方根，四元数的共轭就是矩阵的共轭转置。还有下图的对应关系。这种表示的另外一个好处就是当四元数q=x+yi+zj+wk退化为复数x+yi，即c=d=0时，与之前的复数的矩阵表示是相同的。

第二种是实矩阵表示，把q=x+yi+zj+wk等同于下面四阶实矩阵。

同样的有四元数的模长是矩阵行列式的平方根，四元数的共轭是矩阵的转置。对于退化情形q=x+yi，可见其矩阵表示是复数的矩阵表示放在两个对角块位置上的拼接。

根据k=ij，可以得到q=x+yi+zj+wij=(x+yi)+(z+wi)j，记a=x+yi，b=z+wi，那么q可以视为复数对(a，b)，但由于四元数乘法不满足交换律，所以一般的并不满足类似于复数乘法的关系式(a+bj)(c+dj)=(ac-bd)+(ad+bc)j。只有a,b,c,d为实数时，上述关系式才成立。

因为矩阵乘法一般不满足交换律，这也可以帮助理解四元数乘法为什么不满足交换律，所以四元数形成的代数结构称为四元数体，而不是四元数域。关于四元数的减法，理所应当的定义为对应坐标相减。对于除法，由qq'=|q|²，可以得到1/q=q'/|q|²，这说明与复数除法类似，可以把四元数除法p/q定义为p与q'/|q|²相乘。但是与复数不同的是四元数的乘法不满足交换律，所以左乘与右乘是不同的，也即pq'/|q|²与q'p/|q|²是不同的。那么究竟把哪一个定义成除法更合适呢？其实两种定义都是合理的，只需把p和q间除法区分为左除和右除就可以了，即把除法定义为(1/q)·p和p·(1/q)，分别称为成左除法与右除法，而不把除法写为p/q的形式。

更一般的，还有数系的关于四元数的扩充，例如Cayley八元数。但是八元数乘法既不满足交换律也不满足结合律，所以其作用与四元数相比有些相形见绌。另外也有许多其他种类的数系的扩充，有兴趣的读者可以查阅专门的文献。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

我们刚刚进入了猴年，而数学上竟然有一个与猴子有关的有趣定理：无限猴子定理。而且这还是一个非常著名的定理。

无限猴子定理是来自波莱尔一本1909年出版谈概率的书籍，当中介绍了“打字的猴子”的概念。这个定理是概率论中的柯尔莫哥洛夫的零一律的其中一个命题的例子。不过，当波莱尔在书中提出零一律的这个特例时，柯尔莫哥洛夫的一般叙述并未给出（柯尔莫哥洛夫那本概率论的著作直到1933年才出版）。

零一律是概率论中的一个定律，它是安德雷·柯尔莫哥洛夫发现的，因此有时也叫柯尔莫哥洛夫零一律。其内容是：有些事件发生的概率不是几乎一（肯定发生），就是几乎零（肯定不发生）。这样的事件被称为“尾事件”。尾事件是由无限多的随机变量的序列来定义的。比如它不是与X1的值无关。比如假如我们扔无限多次银币，则连续100次数字面向上的事件是一个尾事件。

关于此定理的叙述为：有无限只猴子用无限的时间会产生特定的文章。其实不必要出现了两件无限的事物，一只猴子打字无限次已经足够打出任何文章，而无限只猴子则能即时产生所有可能的文章。

其他取代的叙述，可能是用英国博物馆或美国国会图书馆取代法国国家图书馆；另一个常见的版本是英语使用者常用的，就是猴子会打出莎士比亚的著作。

不过，还真有人为这个定理做实验。现实的实验中，猴子在使用键盘时通常会连按某一个键或拍击键盘，最终打出的文字不可能成为一个完整的句子。我只能说，要不时间不够长，要不猴子不够多——要无限嘛！

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者：刘洪涛

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

数学在科学技术中的重要性毋庸置疑，在音乐、文学、艺术中的影响人们也并不陌生。数学，它甚至还关乎我们内心的情感。

1

每年公历年底到农历新年除了能不能抢到火车票，漂在各大城市的男男女女还有一个不变的担心是：怎么面对父母的逼婚。

去年情人节时，有一条新闻被各大媒体竞相报道：一个美国的数学家用数学方法找到灵魂伴侣。

数学家麦克金雷失恋9个月后，基本上把美国所有的相亲网站都注册了个遍，结果是偶尔收到网站推荐的人选，发信息过去，基本是石沉大海。

其中有一家名为OkCupid的网站，是四个哈佛数学专业的学生创办的，宣称“用算法来找到你的灵魂伴侣”。这个网站精心设计了若干生活态度和心理测试题，会员们需要回答十个必答问题和若干个附加题目。据统计，该网站会员平均每人会回答350个问题。回答的问题越多，匹配的精准度就越高。—根据这些问题的答案数据，OkCupid的算法引擎会自动测算两个会员之间的匹配度，100%就是数学上的灵魂伴侣。

身为数学家的麦克金雷在这算法中并没有得到什么好处。OkCupid在选择潜在匹配对象时，首先会锁定回答了同一个问题的人群，然后再筛选，最后再根据答案计算两两之间在这个问题上的分值。麦克金雷随机选择问题回答，对他回的这些问题感兴趣的女性很少。所以，在一个拥有8万女性会员的OkCupid，麦克金雷的90分以上匹配者只有不到100个。

一天凌晨，他在电脑上一边编译代码，一边在另一个窗口更新他在相亲网站的资料。突然，他意识到，应该以一个数学家的方式相亲。于是他注册了12个虚拟的OkCupid账号，以数学方法广泛的抓取并分析目标会员信息。

三星期后，他搜集了全国各地20000个姑娘的600万个问题和答案。根据她们的问题和答案，寻找她们感兴趣的东西。他在介绍里强调自己拥有的她们感兴趣的特质。他选出最受欢迎的500个问题，并如实作答，以保证他未来的恋爱和婚姻不是建立在虚假之上。

这样一番努力之后，跟他的匹配度在90%以上的女性会员有一万以上，完全扭转被动局面。最终，他在这些接近完美匹配的女性会员中找到他的灵魂伴侣。

2

从人海中把候选人选出来仅仅是第一步。而大部分单身人士并不是一直缺少约会的对象，很多是因人选太多而不知如何抉择，最后只好喟叹：“曾经有一份美好的感情摆在我的面前，我没有珍惜。”

对于怎么抉择，数学同样有好方法。

大数学家开普勒在他的笔记里留下了他曾经面对的问题。他在夫人染病过世后想再婚，“面试”了11位候选人。第一位给他的印象是卫生习惯不好，淘汰。第二位养尊处优，淘汰。第三位已经和别人订婚。第四位没觉得有什么问题，身材还挺好，不过他想看看第五位。据说介绍人说第五位不错。就在他犹豫中，第四、第五位等得不耐烦，一起走了。第六位是个大小姐。第七位很迷人，也是个急性子，在他看资料的当口，就走了。他对第八位本人没什么印象，却觉得她家庭不错。第九位体弱多病。第十位万人迷。第十一位太年轻。筛选完所有的候选人，开普勒白忙一场。

多年以后，有数学家对此问题提出优化方案。他们的策略是：先面试前36.8%的候选人，但不录用他们。在此之后，一旦遇到比前面这36.8%里更好的就立马录用。11×36.8%≈4，前4个候选人不作考虑，从第五个开始，只要比前4个好就应该求婚，这样便能省去和后面一批人的约会了。

为什么是36.8%呢？这跟概率论中一个重要的数学常数e有关，1/e≈0.368。

如果你预计在最好的年龄遇到的求爱者会有30个人，你应该怎么样抉择呢？想必你已经知道，毫不犹豫先拒绝掉前30/e 个人，静待比这些人都好的人选的出现。30/e≈30×0.368≈11。从第12个人选开始，一旦发现比前面11 个都好的人，果断接受，而不要去等与所有30个人相处过再决定。

3

相亲的过程可以转化为数学问题，相处是否也这样呢？

夫妻矛盾中很大部分的是因为“你对我没有我对你那么好”或“我为家庭贡献得比你多”。双方付出被放到天平的两端比较大小。一旦偏离水平线，关系即面临解体。

这种思维可谓其来有自。在《论语》里，我发现了它的源头：

宰我问：“三年之丧，期已久矣。君子三年不为礼，礼必坏；三年不为乐，乐必崩。旧谷既没，新谷既升，钻燧改火，期可已矣。”子曰：“食夫稻，衣夫锦，于汝安乎？”曰：“安。”“汝安则为之。夫君子之居丧，食旨不甘，闻乐不乐，居处不安，故不为也。今汝安，则为之。”宰我出，子曰：“予之不仁也。子生三年，然后免于父母之怀。夫三年之丧，天下之通丧也。予也有三年之爱于其父母乎？”

宰我说了一大通，什么礼崩乐坏的风险都是借口，核心就是一个，守孝三年时间太长了，一年还勉强。老师回答：你生下来后，父母每天抱着你，抱了三年。轮到你为他们做点什么了，你竟然说一年就够了？！

这里面就是一道比较大小的题：1﹤3。

长久以来，我们就这样看待感情。真的可以怪孔子吗？圣人的心灵是如此简单吗？我们忽略了他回答中最重要的一点，“于汝安乎？”一方的不断付出，你是否接受起来心里毫不羞愧？感情的事，完全存乎一心，常保持一份不安应该就是最好的相处之道。

4

数学被普遍认为是一种语言。在感情表达上，使用什么语言真的是一门学问。巧用数学语言会让你的表达增色不少。在纸条上写一串数字5201314，比直白的“我爱你一生一世”来得浪漫。

有一个关于大数学家笛卡尔的故事。故事说，笛卡尔与爱好数学的公主相爱，遭到国王的反对，他们之间的通信受到严密的检查。聪明的笛卡尔给公主写了一封信，上面没有一句话，只有一个函数表达式：r=a(1-sinθ)。国王和大臣们都不明所以，因而这封信顺利地到达公主手里。在相思成病的公主眼里看到的是一颗饱含深情的心（如图）。

笛卡尔发明了直角坐标系，代数与几何得以结合。把这样一个故事安到笛卡尔的头上，表达了人们对他成就的敬佩。

5

人类可以用数学来表达爱，数学本身也有爱。瞧，一群数字在互相表白心迹：

9对3说：我除了你还是你。

旁边的4听到了，伤心的哭了：我除了2还是2，我是2到家了我。

0对1说：我除了你，什么都没有。

1对0说：我除了你，一切都没有意义了。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

作者：伊恩·斯图尔特，英国沃里克大学数学教授,因其大量优秀的数学科普作品而响誉世界。

《给年青数学人的信》是作者伊恩·斯图尔特尝试部分更新《一个数学家的辩白》，也就是说，更新那些或许会影响一个年轻人的决定，如考虑取得数学学位和可能的数学专业生涯。这些给“梅格”的信件大致遵照时间先后，从她高中一直写到在大学获得永久教职为止。书中讨论许多的议题，包括最初关于职业生涯的决策到职业数学家的工作哲学，以及数学家研究题材的本质，不只有一些实在建议，还提供来自数学圈子内的见解，并且解释数学家到底在做什么。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

第一封信 为何学数学？

亲爱的梅格!

或许如你所预期，得知你考虑攻读数学时，我非常高兴。不只是因为数个夏天前，你用数星期反复阅读《时间的皱纹》（A Wrinkle in Time）的时间并未白费，同时也不枉我费心对你解释超立方体和高维空间。我不依顺序回答你的问题，先回答其中最实际的问题：除了我以外，有谁真的靠数学维生？

这个问题的答案和许多人所想的不一样。我所服务的大学在几年前对校友进行调查，发现在种种学位之中，有数学学位的人平均收入最高。需要提醒你的是，虽然这是在他们成立医学院之前的事，但至少驳倒一项谬论：学数学的人无法拥有高收入的工作。

事实是我们每天到处都可遇到数学家，只是很难察觉而已。我过去的学生有的管理酿酒厂、创立他们自己的电子公司、设计汽车、编写计算机程序和在股票市场交易期货，我们几乎从未认识到银行经理或许拥有数学学位，发明和制造DVD和MP3播放器的人们中有很多是数学家，或是将木星卫星令人惊异的照片传输至地球的技术里也包含大量的数学。我们知道医生有医学学位，律师有法律学位，因为那些是特殊和明确定义的专业，要求同等专业的训练。但人们不可能在建筑物的铜制铭牌上发现有证照的数学家的名字，替该数学家打广告：这位数学家在获得一大笔费用后，可以帮忙解决想要解决的任何数学问题。

我们的社会消费了大量的数学，但一切只在幕后进行，原因相当直接：数学属于幕后。当驾驶一辆汽车，你绝对不想考虑所有那些复杂的机械方面的东西，只想钻进车子里将它开走。了解车子机械的基本状况，当然对你成为好的驾驶员有所帮助，但绝不是一定要这样才行的。同样地，数学也是如此。你希望车子的导航系统引导方向，而不需自己来计算所涉及的数学。此外，你希望即使不了解信号处理和误差修正码，你的电话仍可以运作。然而，我们其中的一些人需要知道如何运算数学，否则上述的汽车和电话将无法运作。如果其他人能够了解我们日常生活是如何必须依靠数学，那将是一件好事。为何将数学远远放在幕后，这是因为许多人完全不知道数学藏身在幕后。

我有时觉得，要改变人们对于数学的态度，最好的方式是，在任何用到数学的东西上贴上写着“内含数学”的红色标签。当然在每一部计算机上都会贴上一张，又如果照字面的解释，我们也应该在每一位数学老师身上贴上一张。我们也应该将红色数学标签贴在每一架飞机、每一部电话、每一辆车、每一个交通标志、每一种蔬菜……

蔬菜？

是的。农夫只是照着他们父亲和祖先流传下来的模式耕种，这种日子早已过去。几乎所有你能买到的蔬菜，都是长期和复杂商业培植计划的结果。“实验设计”数学意义上的整个主题，在二十世纪早期被发展出来，用来提供一个系统的方式去评估新种的植物，遑论基因修改的较新方法。

等等，这不是生物学吗？

当然是生物学，但也是数学。基因学在生物学里最早使用数学，人类基因组计划之所以成功，不只是因为生物学家做了许多明智的工作，也因为发展出强大的数学方法，用以分析实验结果，并且从非常破碎的数据里重建准确的基因序列。

所以，蔬菜得到一个红色标签。如同蔬菜，其他东西也应贴上一个红色标签。

你看电影吗？你喜欢特效吗？《星球大战》（Star Wars）和《魔戒》（Lord of the Rings）里面有数学？ 最早的完全计算机动画电影《玩具总动员》（Tory Story），促成了大约二十篇数学论文的发表。“计算机绘画”不只是使用计算机来做画，也是让图画看起来更真实的数学方法。为了做出这些效果，需要立体几何的知识、光的数学，以及在起始和完成的影像间内插一连串平滑的动作，等等。“内插”是一个数学的想法，如果没有许多聪明的数学，内插将不会产生作用——又一个红色标签！

当然还包括因特网，完全是数学运作。目前最主要的搜索引擎Google使用数学方法，根据矩阵代数、概率理论和网络的组合数学，去寻找最可能包含用户所需信息的网页。

但因特网的数学较这些更为基本。电话网络依赖数学，它不像旧时，当时接线生必须手动将电话线路插入总机，而今天这些电话线必须同时传输数百万个信息。有太多人想要和朋友谈话、传真或上网，以致我们必须分享电话线、海底光缆和卫星中继器，否则网络无法承受那么繁忙的交通。所以每一段谈话都被分解成数千个小段，只有约1%的小片段被实际传输，其余的99%借着填补间隙的方式尽可能地被复原（之所以行得通，是因为取样虽短但频率非常高，以致你声音的改变比取样的间距来得慢很多）。噢！整个信号被编码，以致任何的传输错误不仅可被检测出来，也可重新放到正确的接收位置。

如果没有大量的数学，现代通信系统将无法运作。编码理论、傅立叶分析（Fourier analysis）、信号处理……

总之，你上网购买机票、订位、前往机场、坐上飞机后飞往他处。飞机之所以能够飞行，是因为工程师使用流体流动和空气动力学的数学进行设计，确保飞机可以飞在天上。飞机使用全球定位系统（简称GPS，定位系统由一组卫星构成）来导航，卫星信号经由数学分析，可以在数英尺的误差内告诉你飞机的位置。每一个航班都必须列入时间表，才能让每一架飞机处于正确的位置，这需要其他领域的数学。

亲爱的梅格，这是数学运作的方式。你问我数学家是否都隔绝在大学里，或是否有部分数学家的工作和实际生活有关。其实你实际生活的全部，就如同一艘在数学海洋里徜徉的小船，上下摆动。

但很少有人注意到这一点。逃避数学会让我们感到自在，但却贬损了数学。这真可耻，这样一来，人们认为数学没有用处、不必在意，数学只是智力游戏而已，没有真正的重要性。因此，我才想要看见那些红色标签。事实上，不用红色标签的最佳理由，是大部分的地球都将被红色标签所覆盖。

你的第三个问题最为重要，也最令人哀伤。你问我是否必须放弃对美的感受以研读数学，是否所有事情将变得只剩下数字、方程式、定理和公式。梅格，敬请宽心，我不会怪你问这个问题。可惜这是个非常普遍却错得离谱的想法，和真相恰好相反。

数学对我而言如下：它让我以全新的方式知觉这个我所居住的世界，让我对自然的定律和模式开了眼界，并提供全新的关于美的经验。例如，当我看见彩虹，我不仅是看到一道光亮多彩的圆弧，也不仅是看到雨滴对阳光的影响，雨滴将白色日光还原为构成日光的色彩成分。我发现彩虹既美丽又启发灵感，对彩虹不仅只是光线的折射而心存感激，这些颜色就像红色（还有绿色和蓝色）的鲱鱼。彩虹的形状和亮度需要解释：为何是圆弧状？ 为何光线如此之亮？

或许你尚未想过这些问题。你已经知道，当阳光受到雨滴的折射时会出现彩虹，因为阳光的每一种颜色会朝稍微不同的角度转向，并从雨滴反射进入我们的双眼。但事情不是如此简单，为何数以万计雨滴折射产生的数以万计有色光线，不会重叠并模糊掉呢？

答案在于彩虹的几何学。当光线在雨滴内部进行反射，雨滴的球状形体导致光线聚焦于某一特定方向，每一滴雨滴发射出明亮的圆锥形光线，或是说每一种颜色的光形成自己的圆锥体，而每一种颜色形成之圆锥体的角度稍有不同。当我们望向彩虹，我们的眼睛只能侦测到位于特定方向的圆锥体，每一种颜色的方向在天空形成一个圆弧。所以我们看到许多同心圆，每一种颜色形成一个同心圆。你所见到的彩虹和我所见到的，是由不同的雨滴所形成。我们的眼睛位于不同的位置，所以我们侦测到由不同的雨滴所产生的不同圆锥体。

彩虹是个人经验。

某些人认为这样的理解会“破坏”情感的体验，因为它会产生对美感满足的某种压抑，但我认为这是无聊的想法。做这样声明的人通常喜欢假装自己充满诗意，对世界奇妙事物抱持开放的态度，但事实上他们严重缺乏好奇心：拒绝承认世界比他们自身的有限想象来得更奇妙。自然永远比你所想的更深邃、更丰富、更有趣，数学提供你一个非常有用的方式去欣赏自然的美。理解的能力是人类和其他动物最大的不同，我们应该珍视。许多动物都有情绪，但只有人类能理性思考。我必须要说，我对彩虹几何学的理解，为它的美增加了新的光彩，而情感的体验却一点也不会因此变少。

彩虹只是一个例子。我观察动物也和常人的角度不同，因为我注意到动物移动时对应的数学模式。当我注视一块水晶，我留意到原子晶格和外在色彩的美丽。在波浪、沙丘、太阳起落、雨滴落在水坑溅起涟漪，甚至停在电话线上的鸟，我也都能看到数学。此外，如同望向弥漫大雾的海洋，我模糊了解到，这些日常奇妙的事物充满无限的未知。

数学的内在美丽也不应该被轻视、被忽略，数学研究本身就已非常美丽优雅。数学的内在美并不是我们在学校里使用的“加法”。虽然加法背后的一般原则自有其美丽之处，但它们大多难看又无定形。数学的内在美丽存在于：想法、普遍性、突然一闪而过的灵感，以及使用直尺和圆规尝试三等分某个角度就等同于去证明3是一个偶数；我们无法建构一个等边七边形，但可建构一个等边十七边形；没有方法可以解开单结；为何某些无限大比其他还大，而某些应该较大的无限大结果却相等；等于连续平方之和（1+4+9…）的唯一平方数为4900（1除外）。

梅格，因为你有一个合乎逻辑和追根究底的心灵，你有成为优秀数学家的潜力。你不会满意于模糊的论点，你想要看到细节并亲自检查，你不只是想知道如何让事物运作，而且也想知道为何事物能够运作。此外，你的来信让我企盼，将来你能和我目前一样，能够看到数学的有趣和美丽——以一种独特的看待世界的方式。

我希望，这为你研读数学建立了所需要的背景。

关注微信：DuoDaaMath 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa