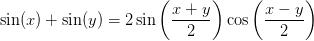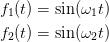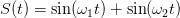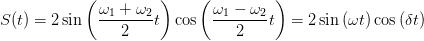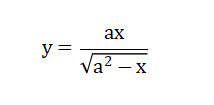2018年10月

物理学家试图用物理挑战黎曼猜想

原文作者，Natalie Wolchover，量子杂志资深作者。

翻译作者，柳北丁，哆嗒数学网翻译组成员。

校对，小米。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

物理学家们正试图将素数的分布映射到某个特定量子系统的能级上。
 
 
以实数（水平轴）和虚数（垂直轴）作为参数的黎曼zeta函数的值。黑色区域是zeta函数返回零的地方——函数的“零点”。所谓的非平凡的零点落在沿着实数部分等于1/2的垂直线上。
 
素数是算术中不可再分解的基本单位，似乎在数轴上随意散布，从2，3，5，7，11，13，17开始，并且没有模式地无限延伸下去。但是在1859年，伟大的德国数学家波恩哈德·黎曼猜测素数的间隔能从其他数字推理出来，这些数字现在称为黎曼zeta函数的“非平凡零点”。
 
 
黎曼ζ函数的输入可以是复数——意思是这样的数“实”和“虚”两种分量——并产生其他数作为输出。对于某些特定复数值输入，该函数返回零作为输出；这些输入是ζ函数的“非平凡零点”。黎曼发现了一个公式，通过对这些零点序列进行求和来计算达到任何给定截断点的素数。该公式还给出了一种方法来测量素数在其典型间距附近的波动——与预期的素数相比，给定素数的大小有多大或多小。
 
 
然而，黎曼知道，只有当ζ函数的零点满足某个特性时，他的公式才是有效的：他们的实部都必须等于1/2。否则，公式没有意义。黎曼计算了ζ函数的前几个非平凡零点，并确认它们的实部等于1/2。该计算支持了他的猜想，即所有非平凡零点都具有此性质，并且因此所有素数的间隔都能从他的函数得到。但他指出，“毫无疑问，如果这个命题有一个严格证明是一件让人满足的事情。”
 
 
一个半世纪之后，证明黎曼假设仍然是纯数学中几乎最重要的未解决的问题，而对这个问题的解答将从克雷数学研究所获得一百万美元的千禧奖。相反，正如理论家恩里科·博比耶里在他对这个问题的描述中所写的那样，“黎曼假设如果是错的会对素数分布的认知造成巨大颠覆”。
 
 
在数学家们从各个角度试图解决黎曼假设的同时，这个问题也转移到了物理学。自20世纪40年代以来，ζ函数的零点与量子力学之间的联系开始变得有迹可循。例如，研究人员发现零点的间距与原子能级的光谱具有相同的统计模式。1999年，在大卫·希尔伯特和乔治·波利亚的早期猜想基础上，两位数学物理学家迈克尔·贝里和乔纳森·基廷推测存在一个量子系统（即一个位置和动量遵从海森堡不确定性原理的系统）的能级完全对应于黎曼ζ函数的非平凡零点。这些能级中的每一个En对应于Zn=1/2+iEn的零点，就是说其实部等于1/2，虚部由En乘以虚数i得到。
 
 
如果存在这样的量子系统，黎曼假设就成为一个直接的推论。原因是量子系统的能级总是实数（与虚数相反），因为能量是一种物理上可测量的量。而且由于这些En是实数，当它们在相应的Zn的公式中乘以i时，它们变成虚数。永远不会有En的虚部与i相乘，从而抵消它的虚数性质使它变成实的的情况，这样它分配到Zn的实部会将偏离1/2。由于能级始终是实的，ζ函数零点的实部总是1/2，黎曼假设也因而是正确的。
 
 
自1999年以来，物理学家一直在寻找这样一种量子系统，其能级对应于ζ函数的零点。在一篇3月30日发表于《物理评论快报》的论文中，圣路易斯华盛顿大学的卡尔·本德、伦敦布鲁内尔大学的多吉·布罗迪和西安大略大学的马库斯·穆勒提出了这样一个候选系统。但它非常得怪异，有外部专家说，现在还不知道是否会引导出一个对黎曼假设的证明。
 
 
通常，物理学家使用高度对称的数学矩阵来描述量子系统，其解或“特征值”对应于系统的能级。这些矩阵的对称性通常保证了虚数部分相抵消，而特征值是实的，这样的话这些矩阵对物理系统的描述才是有意义的。但是20年来，本德和布罗迪研究了量子系统的矩阵描述，这些描述放宽了通常的对称性要求，满足一个叫做宇称时间（parity-time，PT）对称性的弱条件。在2015年与穆勒进行交流之后，他们发现他们可以写出一个PT对称的矩阵，其特征值对应于黎曼ζ函数的非平凡零点。“这结果真是让我们大吃一惊，”布罗迪说。然而，因为矩阵只是PT对称的，而不是遵循通常更严格的对称性，所以不能保证特征值是实的——这个性质确保相应的零点具有等于1/2的实部。
 
 
他们讲清楚了为什么其矩阵的特征值可能是实的，以及为什么在这种情况下，黎曼假设很可能是正确的，但他们没能证明它。“遗漏的证明步骤是困难还是容易，目前我们无法推测，”布罗迪说，“需要进一步的工作来更好地判断这个证明的难度。”
 
专家们表示，这个新的想法很有趣，但关于作者们能否对其不寻常的量子系统的给出严格论证，还很难讲。纽约大学数学家保罗·布尔加德(Paul Bourgade)表示：“我需要更多时间对他们的研究成果对证明黎曼假设的意义给出相关意见。”他还说，他希望更详细地探讨比较他们提出的量子系统与贝瑞(Berry )和基廷(Keating )以前提出的还没能引导出对黎曼假设证明的量子系统。
 
根据布尔加德的观点，如果物理学家真的有一天弄清楚了zeta函数零点的量子解释，那么这甚至可以比黎曼公式更精确地处理素数，因为矩阵特征值遵循非常好理解的统计分布。它还会有其他作用，贝瑞希望，能给出素数分布的量子系统可以作为一个简单的混沌模型，从而演示出与素数相关的混沌行为是如何从一个非混沌的量子系统中产生的。但我们还远没有到那一步。鉴于这么久以来都没有一个对黎曼假设的明确的证明，贝瑞敦促大家保持谨慎的态度，不要过度解读片面的进展。“这对黎曼假设的最新贡献完美体现了皮亚特·海恩(Piet Hein)的格言，”贝瑞说，“值得挑战的难题,必给你带来打击。”
 
 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

唱情歌前的调音？三角函数公式也许能帮你！

原文作者，Enrico Degiuli。

翻译作者，溦之洸茫，哆嗒数学网翻译组成员。

校对，donkeycn。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

有些时候，那些仅从理论角度看上去有意思的数学公式可以揭示与某些应用问题的意想不到的联系。
 
 
以三角学中“和差化积”公式为例
 
 
 
这个公式在解释“差拍”这个声学现象时会有直接的应用，让我们看看这到底是怎么一回事。
 
 
差拍
 
 
 
当你同时弹奏两个频率很接近的音时，合成出来的音听上去时有时无，好像某人在以一个固定的频率调大和调小音量，这种现象就叫做差拍。三角函数公式会帮助我们解释它。
 
 
弹奏的这两个音可以用具有频率ω_1，ω_2的两个三角函数表示（准确地说这两个是角频率，但简单起见，我在这里就把它们称为频率）。
 
 
 
 
作为一个非常好的近似, 我们可以认为声学现象是线性的。如此一来，同时弹奏两个音符产生的声音就等于这两个单音的叠加。
 
 
借助和差化积公式，我们可以将这个“声音”函数表示为
 
 
在最后的表达式中，我们定义了
 
 
 
如果这两个频率ω_1 ~ ω_2很接近，我们可以为认为ω（ω_1 , ω_2的平均值）和这两个频率也是很接近的。同时δ（ω_1 , ω_2的差值的一半）在与ω相比时是一个非常小的量。
 
 
当远远小于时，我们可以认为它是一个对音符sin(ωt)的周期性放缩，放缩倍数为A(t)=2cos(δt)
 
 
我们可以看出，A(t)扮演了一个周期性调节声音sin(ωt)的音量的角色。两个初始频率越接近，那么差拍频率δ就越慢（译者注：δ越小，周期就会越大）。
 
 
 
在下图中，你可以看到一个例子，上图是两个函数 f_1和f_2，下图是它们合成后的函数S。
 
 
下面是对应的声音。最初你可以听到单独的两个音，然后你会听到一起弹奏它们时的效果。
 
 
 
乐器校音
 
 
差拍现象可以用于为乐器校音，让我们看看这是怎么进行的。
 
 
假设你现在需要借助一个音叉来为吉他校音，如果吉他的弦被调到与音叉的音相近的地方时，同时弹响它们就会产生差拍。
 
 
 
通常地说，要通过提高或降低弦的张力来完美校音是很难的。通过反复试错则比较容易。
 
 
我们假设你试图提高弦的张力（也就是提高音的频率），你拨动了这根弦并敲击了音叉，于是听到差拍的频率增加了。这就说明提高弦的张力这法子是走反方向了。此时你应该慢慢减小弦的张力，直到差拍频率小到几乎不会引起注意。现在恭喜你，你的吉他弦与音叉产生的是同一个音(对于实际演奏而言,已经足够了)。
 
 
 
剩下的5根弦呢，过程是一样的，只不过你借助的不再是音叉而是你所调好的那根弦的其他音。（译者注：吉他不同弦上可能会有同一个音，以调好的弦上的音为基准，找它在另一弦同样的音，进而校准这根弦。）
 
 
 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 
当然，你可以借助电脑程序为乐器调音。但假设你现在在海滩或者路边上演奏吉他，周围是你的一群粉丝，而你正好没有电脑、手机没电。你最好知道怎么用传统的方法校准吉他，要不然你会瞬间掉粉的！

2019科学突破奖：小拉福格获数学突破奖，许晨阳获数学新视野奖

根据科学突破奖官网消息，2019年度科学突破奖发布。其中数学奖由来自法国的文森特·拉福格获得。而来自中国的许晨阳获得了科学突破新视野数学奖。该奖官方网站描述许晨阳的所在单位有两个，麻省理工学院和北京国际数学研究中心。
 
颁奖盛典将于2018年11月4日举行。
 
 
文森特·拉福格的获奖理由是：对数学多个领域的奠基性贡献，尤其是对函数域情形的朗兰兹纲领的贡献。文森特·拉福格在中学生时代就在法国数学界小有名气。1990、1991年参加国际奥数竞赛，连续两年获得满分成绩。文森特·拉福格的哥哥洛朗·拉福格也是著名数学家，在2002年北京举办的国际数学家大会上，洛朗·拉福格获得菲尔兹奖。
 
 
而科学突破新视野数学奖颁给了多位数学家。我们最关注的获奖者是来自中国的许晨阳教授，许教授的获奖理由是：对极小模型纲领研究的重大进展以及对代数簇模的应用。我们注意到，在本次“数学新视野”奖的三个获奖席位中，许晨阳是唯一一位独占一个获奖席位的得主。1999年至2004年，许晨阳在北京大学数学科学学院学习，获学士和硕士学位。再联想到去年同是北大数学科学学院毕业的恽之玮、张伟也获得过该奖，这段时期北京大学数学专业的“人才井喷”并非虚言。
 
 
科学突破奖为世界上奖金最高的学术奖项，由Facebook创立者扎克伯格夫妇、俄罗斯互联网巨头米尔纳夫妇、中国阿里巴巴集团创始人马云夫妇、谷歌创立者之一布林与23andMe公司创立者沃西基夫妇共同创立。此奖项共设立生命科学、基础物理、数学三大奖项。每个获奖席位300万美元奖金。另外，还为物理和数学的“学术新人”设立了科学突破新视野奖，每个获奖席位60万美金。所谓获奖席位，是指在学术研究中，可能有多个人做出相同成果，如果超过一个人的研究者用因为相同的获奖理由得到奖金，那么这几位研究者平分该席位的奖金。本次颁奖为此奖项的第七次颁发。按官网介绍，会有2200万美元的奖金发出。

驳网易：你凭什么让奥数滚出童年

作者，e^iπ+1=0

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 
 
6月20日网易下属浪潮工作室发表文章题为“请奥数滚出中国小孩的童年”[1]（下用“奥数童年”做简写指代此文），而笔者关注的某公众号推送此文，由于题目措辞之激烈，不由得点入阅读。笔者读罢，认为文章中的某些观点并不坚实，故作此文，提出一些不同的见解。
 
 
“奥数童年”首先梳理了国际奥林匹克数学竞赛的起源，而后是中国奥林匹克数学竞赛的发展历史，最后是中国奥林匹克数学竞赛的封禁史。
 
文章的主要观点如下：
 
一、奥数竞赛本质目的是为了选拔真正的数学天才，而中国的奥林匹克数学竞赛则是提高中国学生的整体水平。
 
二、由于没有统一标准的考试决定“小升初”，所以初中学校为选拔好学生，将奥数竞赛成绩作为选拔标准之一，导致奥数竞赛辅导过热。
 
三、奥数训练在中国不受孩子欢迎。
 
四、中央和地方对奥数从开办开始就不信任，以至于后来教育部逐渐封禁奥数加分，奥数保送资格等。（“为什么政府对奥数如此介怀？原因之一大概是，除了作为选拔机制扰乱义务教育的公平性，并给教师增加了外快渠道，奥数本身——真的没啥用。北京理工大学教育科学研究所的杨东平，直接称奥数为“社会公害”，说它“完全违反教育规律”。”）
 
五、奥数只适合极小部分人学习。（“中科院院士、数学家张景中认为只有5%的人适合学习奥数，而北京理工大学的教授杨东平甚至认为5%这个数字都期望过高，应该在3%左右。而即便对于这3-5%的人来说，奥数也并非他们人生路上的指路明灯。”）
 
六、对于参加奥数的学生，在长期回望来看，既对除数学以外的其他领域成就没有帮助，也对学生在社交与心理上没有帮助，甚至有“毒害“。
 
文章提出的观点，是十分具有代表性的观点，且全面，几乎包括了笔者在网络上看到关于奥数竞赛讨论的所有质疑观点，总结而言主要是这样三个问题：一、奥数增加了绝大部分小学生不必要的负担，因为他们不适合学习奥数。二、奥数对于人的长远发展不仅没有正向帮助，甚至有负面影响，而且对于学术界和社会的贡献不大。三、中央和地方不支持奥数教育。笔者将对这些观点，结合文献和事实，提出不同的见解。
 
1.中国奥林匹克数学竞赛的目的是选拔优秀的数学人才，并得到国家支持
 
中国最早诞生的并不是现在饱受诟病的小学奥数竞赛，而是在高中数学竞赛。早在二十世纪五十年代中期，在老一辈数学家苏步青，华罗庚等的指导下，我国就举办了第一次数学竞赛，而由于政治运动影响，这一活动时断时续直到1964年。而这段时期的成就被评价为[2]：“在数学方面才能突出的学生被集中起来并给予特殊的教育；中国的整体数学指导水平得到提升；数以千计的中国学生被鼓励参加学习小组学习课外数学知识；这对美国建立数学奥林匹克竞赛提供了经验。“其评价是正面且高度赞扬的。
 
Fig.1 中国数学奥林匹克竞赛的案例研究
 
而1979年之后，在华罗庚教授的倡导下，我国大陆上的29个省、市、自治区都举办了中学数学竞赛。1980年，在大连召开的第一届全国数学普及工作会议上确定将数学竞赛作为中国数学会及各省、市、自治区数学会的一项经常性工作，每年下半年举行“全国高中数学联赛”。所以针对文中“于是国务院批复教育部，“五年之内不再举办类似的全国竞赛活动”。 从那以后，国内的奥数比赛和政府脱离了关系，成为了民间赛事，由各省市的数学会承办。“传达的信息，笔者认为是有失偏颇的，全国性质数学竞赛并不是被禁止，而是成为中国数学会及各省、市、自治区数学会的一项经常性工作。这标志中国数学竞赛成为了一个常规性，规范性的赛事。
这里需要简单介绍一下中国数学会。中国数学会是中国数学工作者的学术性法人社会团体，是中国科学技术协会的组成部分。中国数学会的主要工作有：组织学术交流活动，编辑出版数学刊物，开展国际学术交流，举办数学竞赛，开展普及工作，组织促进数学教育改革的活动，根据国家建设和学科发展的需要举办培训班或讨论班等。[3] 而中国科学技术协会是中国科学技术工作者的群众组织，是中国共产党领导下的人民团体。其领导体制是属中直系统，由中央书记处直接领导。[4] 由此可见，中国数学会并不完全是一个“民间组织“，而”奥数童年“中的措辞是不准确的。
 
2.数学奥林匹克竞赛无论是对学术界还是人的长期发展都有帮助，并不是极少数人的狂欢
 
“奥数童年“中列举论据，包括教育专家与数学家对于奥数的观点，台湾师范大学的团队对奥赛选手的调查，2010年针对苏联奥数学生的研究以及对于”付云皓事件“的评论，认为奥数实则毒害人。由此认为，奥数对于人的长远发展不仅没有正向帮助，甚至有负面影响，而且对于学术界和社会的贡献不大。
针对这些论据，笔者查询了原文章[5]，认为可从中得出不同的结论。首先是文中提及台湾大学的团队对奥赛选手的调查，事实上这个调查的主要结论并不只有这一条。在摘要中提到，这些选手在班级中的排名很好，而他们的对于数学和科学的态度积极，有自我学习能力，有创造性解决问题的能力等特征。这些特点却被“奥数童年“忽略了，这是不客观的。
 
Fig.2 台湾团队研究报告的摘要
 
其次，罗马尼亚数学科学学会的2014年的一篇文章[6]指出，有36位获得IMO奖牌获得者，分别获得菲尔茨奖，沃尔夫奖，凯莱奖等数学界重要的奖项，而其中罗马尼亚数学家出现了四次。而文章的结论是：数学竞赛是成为数学家的重要因素，但不是唯一因素，这不是唯一的方法让人喜爱数学。
 
Fig.3 罗马尼亚数学科学学会的文章结论
 
而关于张景中院士提到的，奥数只适合5%的孩子学习，这话却是有背景的。中国新闻网2015年10月16日的新闻，文章标题为：“提倡凭兴趣学奥数“。[7] 而文章中亦提到：” 数学是门很有意思的学科，学数学可以养成科学看问题的思维方法，且目前各个行业都离不开数学，可以说，当下是数学的世纪。“；” “其实，人群中只有5%的人适合学奥数。”张景中以高考题量做比分析称，高考数学二十多道题考两个多小时，奥数只有3道题目可能需要4个小时，“奥数更多是一种思维，学习奥数不能强迫，有兴趣的学生应当给予适当引导。”“观点鲜明，并不是强调奥数不适合绝大多数人学，而是如何学，学什么的问题。笔者在初中的时候参加学校的奥数竞赛班，老师就曾推荐过张景中院士的几何新方法和新体系，属于”走进教育数学“丛书。在初中竞赛中，学习过平面几何知识的同学都知道”三点共线“的梅涅劳斯定理，以及”三线共点“的西瓦定理。这两个定理无论是证明还是应用都是十分重要的，既可以从传统的欧氏几何的角度理解，也可以从射影几何的角度了解，又可以从立体几何的角度获得启示。而此书则从”消点法“开始，利用面积消点的方法由浅入深地解决了一系列射影几何问题，其中梅涅劳斯定理的证明时至今日仍让笔者惊叹，而对数学的喜爱从那时起再未停止，一直到现在。[8]而这一观点则引出机械证明数学定理的想法并逐步展开。此等风景是在课内看不到的，但是其思想并没有艰深到只有5%的学生才能理解。所以张景中院士的话私以为绝不是让人不要学，而是教人想清楚学什么，怎么学，是一个教育学命题。
 
 
Fig.3 几何新方法和新体系
 
 
关于“付云皓事件“的讨论，在题为《奥数天才坠落之后.》的文章与知乎上付云皓回复《. 奥数天才坠落之后——在脚踏实地处 付云皓自白书.》这一来回中，已经引起广泛的讨论，笔者不着过多笔墨讨论。但是”奥数童年“写道：“事实上，付云皓才是那个真正走出了奥数毒害的人，最终过上了正常人的生活。”这一观点，笔者恕不敢苟同。并不是奥数毒害了付云皓，事实上他并未远离数学，而正在为改善中国数学基础教育质量做出贡献。（“现在的我，正稳稳当当地一步一个脚印踩在基础教育的道路上，在广东第二师范学院这所以培养中小学老师为目标的学校。” 出自付云皓在知乎的回应[9]）这一点上，他既普通，就如我国千千万万为数学教育事业做出贡献的工作者，也不普通。
 
结语
 
关于奥数教育这个话题是可以一直谈下去的，因为中国奥数教育的确给中国孩子带来很糟糕的体验，导致很多孩子还没学会欣赏数学，就已经磨灭了兴趣。这是我们的数学教育可悲的地方，但是这是因为数学吗？笔者认为不是，而是功利的教育思路，而功利的思路往小了说是由于优质教育资源的稀缺以及基础教育水平较低，往大了说是由于社会资源的不可避免的不公平配置，这并不是因为奥数的初衷所导致的。私认为奥数踢出中国孩子的童年实际上只是一个治标不治本的话，奥数被踢走可能还会有艺术学习（器乐，声乐，舞蹈，书法等），还可能是新的技能比如编程。只要有激烈的竞争存在，用什么来竞争就变得不那么重要了，而是竞争本身的属性会异化一切被用来竞争的对象，很不幸，奥数是其中之一。而对奥数的厌恶甚至成为很多学生讨厌数学的一个开口，这恐怕是最悲哀的地方了，这也是社会和家庭再数学教育上需要做出努力的地方。
最后，一个有趣的事实是，笔者此文中的参考资料或者引述文献基本来源于“奥数童年”，但是笔者却得到了和原文不同的结论，读者可以对比阅读，或者查阅这些文献，欢迎讨论。
 
附：
早在2010年就有工作室给出文章讨论这个问题，推荐：
http://www.360doc.com/content/10/1218/11/5148659_79208210.shtml 来源：本明工作室
 
 
Reference：
[1] 吴静宣 (2018) 请奥数滚出中国小孩的童年 浪潮工作室  https://mp.weixin.qq.com/s/uVLA2xzi5m_MtgCwfeChwA
[2] Swetz, F. (1972). The Chinese Mathematical Olympiads: a case study. The American Mathematical Monthly, 79(8), 899-904.
[3] 中国数学会简介 http://www.cms.org.cn/about.html
[4] 中国科学技术协会简介http://www.cast.org.cn/n200595/n201286/index.html
[5] Wu, W.-T. (1996). Growing up in Taiwan: The impact of environmental influences on the math olympians. International Journal of Educational Research, 25(6), 523–534. doi:10.1016/S0883-0355(97)86729-8
[6] Vasile Berinde, Radu Gologan (2014). Is there an impact of mathematical competitions on the development of mathematical research? The Romanian experience. Revista De Politica Ştiintei Si Scientometrie.
[7] 中国新闻网 (2015) 中科院院士张景中：“提倡凭兴趣学奥数” http://www.chinanews.com/sh/2015/10-16/7573658.shtml
[8] 张景中 (2009) 几何新方法和新体系 科学出版社
[9] 付云皓 (2018) 奥数天才坠落之后——在脚踏实地处 付云皓自白书 知乎
 
 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关于这两天黎曼猜想消息传言：还没到庆祝的时候

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

本来关于这个，在论文没有正式公布前，我们哆嗒数学网的小编本来什么都不想说，但不断有人“提醒”我们应该说一说——微信提醒、QQ提醒、各种私信提醒——于是我们还是说一说吧。

 

首先澄清，之前不在公众号发布这个消息，是因为这本来是别人小圈子的内部讨论班，该讨论班的参与和组织者并没有希望把此事在这个时候就变成公共事件。我们不报到也是因为不想影响当事人师生的正常教学授课秩序，与当事者的名气、国籍无关。这不，原定的的讨论班时间被一波莫名其妙的舆论搞得推迟了不是。

 

最新消息是，网传黎曼猜想的证明在10月13日由李忠教授在中科院数学所南楼某教室的讨论班上公布。这个消息被汤涛院士在他的微博“数学文化”上发布。我们也多方打探，这个讨论班的确存在过。

 

 

关于对定理猜想证明的态度，我们知道的有两种：

 

一是网传的郑忠国老师、彭立中老师两位北大数学教授对证明的肯定，认为李忠教授的确证明了黎曼猜想。

 

另外一种就说得比较婉转：“李教授和阿蒂亚爵士都是80多岁的人了，还在勇攀高峰，令人敬佩。他们的证明大家别讨论了，他们的健康才是我们最关心的。”

 

至于哆嗒数学网的小编们的态度？当然是“谨慎的不乐观”，之前对阿蒂亚是这样，现在对李忠教授也是一样。

 

等到论文出世，同行评议，确定结果的时候大家再“高潮”吧，现在真还不是时候。你看，我上面写了那么多文字，前面都要加个“网传”，你们现在在朋友圈兴奋啥呢？

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

我们人类能在四维空间里活下去吗？

 

原文来自AskAMathematician网站。

翻译作者，ALIMJAN，哆嗒数学网翻译组成员。

校对，小米。

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

提问：人能在四维空间里活下去吗？
 
 
回答：不能。 但要理解为什么，先得知道什么是维度。当有人说“我们生活在一个三维世界”时，他真正应该说的（若要十分精确）是 “我们居住的宇宙有三个空间维度”。 有几种方法可以说明你生活在一个三维世界中。 最简单的就是尽可能多地找出相互垂直的方向; 你能轻松地找出三个方向，但你永远找不到第四个方向。
 
 
 
 
这三个方向是相互垂直的，并且没有其它的方向能同时垂直于这三个方向。
 
 
 
如果你感觉非常聪明，你会发现很多其他能展现我们所处的宇宙的三维特性的例子（而不是两维或四维）。例如，如果你能打出一个简单的结，那么你能展示我们肯定生活在三维或更多维度（二维的情形是无结的），如果你能制作一个克莱恩瓶，那么你会是在展示我们绝对生活在四维或更多维度的世界里。
 
 
 
在两维空间中，如果你要让绳子打结，那么你就必须让绳子穿过自身。在三维空间中也同样无法生成一个克莱因瓶。这两个难题的本质是一样的。
 
 
 
维度是一个方向。 生活在一个多个维度世界是指你有多个方向可以移动。生活在多个维度会产生许多怪异的物理效应，而是第一个你会注意到是立即死亡。（我们假设你不知何故突然出现在一个四维的宇宙）
 
 
一个实际的二维生物在三维世界中会坍塌，并且我们没有办法能区别它的外部和内部。被认为是它的内部的东西，在我们这些三维的家伙看起来更像是它的表面。
 
 
如果一个“二次元娃娃”（一个二维的生物）突然被带入到一个三维空间，它的所有内脏都将会变成“外脏”。同样地，因为没有什么在第四个方向上支撑着你的身体，所以如果你发现自己处在有额外维度的空间，那么你的内部会顺着最小（或零）阻力的路径而解体。这将会超级恶心，但也就仅仅是像一层无限薄的浮油而已。任何真正的四维生物甚至都不会察觉到。
 
 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

用多项式来表示布尔逻辑

原文作者，Jeremy Kun，伊利诺伊大学数学博士，谷歌工程师。

翻译作者，donkeycn，哆嗒数学网翻译组成员。

校对，Math001。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 
 
问题：用一些多项式来表示布尔逻辑表达式。即：若每个输入变量x取值为0（对应于假）或1（对应于真）。则一般地，对应的多项式的输出值应根据表达式的真假而分别为1或0。
 
解答：只需一个多项式。
 
 
举例说明：表达式┐[(a∨b)∧(┐c∨d)]，即：非((a或b)且(非c或d))。
 
诀窍是：碰到“且”就用乘法，碰到“非”就用1去减。于是，“a且b”就对应于“x1 x2”；“非z” 就对应于“1-z”。事实上，如果你有两个二值变量x、y，那么xy为1，当x、y都是1时；为0，当x、y有一个为0时。类似地，1-x为1，如果x为0；为0，如果x为1。
 
 
再结合德·摩根律就可以得到任意表达式了。a∨b=┐(┐a∧┐b)对应为1-(1-a)(1-b)。对于我们上面的例子：
f(a , b, c, d) = 1-(1-(1-a)(1-b))(1-c(1-d)).
展开，得：
1-a-b+ab+(1-d)(ac+bc-abc)
 
 
如果你代入a=1,b=0,c=1,d=0，你就可以得到原来的表达式的值为“真”（因为“非c或d”为“假”）。同样地，对应的多项式的运算结果为
1-1-0+0+(1-0)(1+0-0)=1.
 
 
你可以用下面的列表作为参考，来验证其余的工作：
 
0, 0, 0, 0 -> 1
0, 0, 0, 1 -> 1
0, 0, 1, 0 -> 1
0, 0, 1, 1 -> 1
0, 1, 0, 0 -> 0
0, 1, 0, 1 -> 0
0, 1, 1, 0 -> 1
0, 1, 1, 1 -> 0
1, 0, 0, 0 -> 0
1, 0, 0, 1 -> 0
1, 0, 1, 0 -> 1
1, 0, 1, 1 -> 0
1, 1, 0, 0 -> 0
1, 1, 0, 1 -> 0
1, 1, 1, 0 -> 1
1, 1, 1, 1 -> 0
 
 
讨论：这一技巧被广泛应用于计算机科学理论中，将布尔逻辑嵌入到多项式中。显然，之所以称之为“布尔代数”，是因为它的确是代数的一个子集。
 
 
 
此外，由于布尔可满足性问题：“用算法来确定布尔表达式是否可满足（选择一组变量的值使表达式的值为真）”是NP难(NP-hard)的，这可以用来表明与多元多项式有关的某些问题也是非常困难的。例如，求多元多项式的根（这里甚至可以假设你对代数几何一无所知）是很困难的，因为：即使你只是简单地考虑来自布尔表达式的那些多项式也将是NP难的。
 
 
 
这里有一个更有趣的例子，涉及到在现代机器学习中出现的优化问题。现在设想一下你要优化一个在一组二次等式约束下的多项式f(x)。这也是NP难的。而下面简单解释一下原因。
 
 
 
设φ是一个布尔表达式，f_φ是对应的多项式。首先，多项式中使用的每个变量xi可以通过约束x_i(x_i - 1)=0被限制为只能取0、1二个值。
 
 
你甚至可以证明：哪怕需优化的目标函数仅仅是二次的，它依然是一个NP难的问题。作为练习，可以将子集和的问题表示为使用类似选择作为约束条件的二次规划问题。据此，你甚至把子集和表示成具有线性约束的二次规划问题。
 
 
 
最后话说回来，这篇文章的重点很简单，多元多项式可以编码任意的布尔逻辑表达式。
 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

200多年前，剑桥大学的数学考试题目

原文来自Reddit论坛的帖子。

翻译作者，Humphrey Liu，哆嗒数学网翻译组成员。

校对，Math001。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

其实这套题，前面还好。到后面各种古董装置的出现，就有点不好办了。
 
 
1、已知年利息率为5%，求360.10英镑存3个月所得利息。
 
 
2、 0.5416天 = (    )小时=（   ）分钟=（   ）秒
 
 
3、 法制圆周角是400°，则法制7.928703°=英制（    ）°（    ）′（    ）″（英国人圆周角360°）
 
 
4、 证明：任意三角形的三个内角和等于两个直角。
 
 
5、 构造一个正方形使得它的面积等于已知多边形的面积。
 
 
6、证明：半圆上的圆周角是直角；优弧上的圆周角大于直角，劣弧上的圆周角小于直角
 
 
7、证明：在一个直角三角形中，作斜边上的高，所得两个新的直角三角形与原直角三角形相似，它们也彼此相似。
 
 
 
8、 利用圆给出正切的定义，画出135°的弧对应的正切线，并用67°30′的正切值表示135°的正切值。
 
 
9、 在一个直线型三角形中，已知两条边和夹角。研究另外两个角的计算公式;借助对数,应用这个公式解决如下问题：已知三角形的两个边长为562和320,夹角128°4′，求另外两个角。
 
 
10、 通过一个例子，解释并证明关于直角球面三角形的纳皮尔法则。
 
 
11、在椭圆中，证明短轴是长轴和通径的比例中项。
 
 
12、 在椭圆中，证明共轭直径的平方和是一个常数;
即.  AC²+ CB²=CP²+CD²
 
 
13、如果一个圆柱体被一个平面相对于轴斜切，求截面的形状？
 
 
14、证明二次方程解的求根公式; 并在已知两根和与积的情况下，求出根的表达式。
 
 
15、 给出等差数列前n项和的表达式，并应用此公式计算首项是1，公差是7的等差数列前n项的和。
 
 
16、 在平衡理论中，证明力的合成基本命题。
 
 
17、 物体作匀加速度下落时，证明物体由静止开始下落的空间位移与时间的平方定律; 根据这个定律，在物体下落n秒过程中，求出最后两秒物体的位移。
 
 
18、 解释什么是钟摆的摆长; 根据摆长的变化，以及振动时间的误差，给出一个公式，可以计算出相应的引力或重力的变化。
 
 
19、 解释普通虹吸管的构造，工作原理和操作方式。
 
 
20、 解释并举例说明液体比重计的构造和使用。
 
 
21、解释哈德利象限仪的构造原理及使用方法；
 
 
22、解释常用天文望远镜的构造;并说明制约其放大倍数增大的原因。
 
 
23、 确定一个地方纬度的最佳方法是什么?
 
 
24、解释船舶在海上确定经度的方法。
 
 
25、如果两颗恒星位于二至圈,在它们北极距离不变的情况下,赤经的差为180°; 如果这种偏差是由地轴自转轴的章动引起的，那么它们在北极距离上最大偏差的比例应该是多少呢? 根据布拉德利的光行差理论，最大偏差的比率是多少?
 
 
26、解释术语：平均近点角和真近点角; 并描述开普勒问题的用途（开普勒问题提出了从平均近点角中寻找真近点角的方法）。
 
 
27、阐述牛顿提出的万有引力定律; 根据万有引力定律，解释牛顿推断的现象：木星的卫星被吸引朝向木星。
 
 
28、分点岁差是什么意思?岁差的值是如何通过观察确定的? 牛顿对其原因的解释是什么?
 
 
29、如果地球沿着椭圆轨道运动，太阳位于一个焦点，证明：万有引力与离太阳的距离平方成反比。
 
 
30、给定以下曲线画图，其中x为横坐标，a为给定的常数，并计算曲线下面积。曲线为：
 
 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa