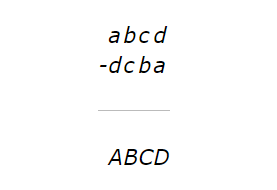2019年8月

不用加减乘除如何描述实数？

 

本文编译自 @downwardsLST 的推特账号

编译作者，Math001

 

关注 哆嗒数学网 每天获得更多数学趣文

 

 

有很多定义实数的办法，他们之中很多都是等价的。但是，如果我想放弃所有的代数结构，只是使用序结构来定义，会怎么样呢？(就是说只考虑大小关系，不考虑加减乘除之类的运算)。首先，我需要一个全序集——这样的集合里任意两个元素都可以比较大小。

 

 

自然数就是那样的集合，而且每个自然数都有一个后继。但是，我们想让自然没有端点，于是我们加入“没有最大元素和最小元素”这样的条件。好了，这样整数就诞生了。但是，这样的集合有太多的缝隙，每两个连续的整数间都有缝隙。

 

 

我们需要填补这些缝隙，于是需要打破每个整数都有前驱或后继这样的状态。于是，我们这样要求，要求任意两个不同元素之间都有另外一个元素：这个性质叫做(序)稠密性。

 

 

看吧：有理数就是稠密的。但是，有理数仍然有很多“小洞”。为了填补这些洞我们要求“完备性”：每一个有界子集都有上确界和下确界。实数就满足这样的性质，填补那些洞的数叫做无理数。

 

 

但是，我们还要现在我们得到的实数不能“太散了”，所以还需要加入条件：如果有一串开区间两两不交，那么这一串开区间至多可数。所以有个问题是这样的：以上的这些性质是不是就能刻画实数？

 

 

这就是“苏斯林假设”( Suslin Hypothesis, 简称SH)。舒斯林假设说：如果一个有序集合满足之前说的所有条件，那么他是否和实数（通常意义的实数）是同构的（这里指序同构）。

你也许已经猜到了：苏斯林假设在ZFC公理体系下不可判定。

 

关注 哆嗒数学网 每天获得更多数学趣文

中国数学家张伟获得克雷数学研究奖

关注 哆嗒数学网 每天获得更多数学趣文

 

 

根据克雷数学研究所官网消息。中国数学家，麻省理工学院教授张伟因其在算术几何、自守形式的算术方向的开创性贡献获得2019年度克雷数学研究奖。这是中国数学家首次获得该奖项。

张伟，2000至2004年就读于北京大学数学科学学院并获理学学士学位，2009年获得哥伦比亚大学博士学位。现任麻省理工学院数学系教授。在此之前，曾获2010年SASTRA 拉马努金奖、2013年斯隆研究奖、2017年西蒙斯奖，并受邀于2018年在巴西里约热内卢举办的国际数学家大会上作邀请报告。

此次奖项由克雷数学研究所(Clay Mathematics Institute)颁发。克雷数学研究所是非盈利私营机构，总部在美国麻萨诸塞州剑桥市。机构的目的在于促进和传播数学知识。它给予有潜质的数学家各种奖项和资助。而一年一度的克雷数学研究奖已经成为数学界的重要奖项。

 

 

克雷数学研究所最为人熟知是它在2000年5月24日公布的七大奖难题，俗称千禧年问题。这七道问题被研究所认为是重要的经典问题，包括黎曼猜想、P/NP问题、庞加莱猜想等数学界最关注的问题。解答任何一题的第一个人将获颁予一百万美元奖金。目前仅有庞加莱猜想被解决。

 

关注 哆嗒数学网 每天获得更多数学趣文

数据科学家会成为未来新的的大祭司吗？

 

原文作者：Conrad Wolfram，软件技术专家。

翻译作者，聂海波，哆嗒数学网翻译组成员。

校对：小米、蘇溯

 

 

 关注 哆嗒数学网 每天获得更多数学趣文

 

 

我们的民主制度今天面临着巨大的挑战。选举的成败取决于大众相信什么。一小撮精英，通过他们所独享的信息来操控我们的思想，而大多数民众则被排除在外。

 

我所谈论的是现代数据科学，以及更加普遍的计算技术在我们的社会中的压倒一切的影响。只有一撮人，学习过如何将计算思维直接应用于信息处理、论证和做必要的决策。这其中包括了关于政府、投票的事情。

 


当然，这种精英控制以前就已经发生过，事实上，这种事情在最近几个世纪才被消除。这一变化有一个关键的推动因素：阅读教育的普及。


过去，很少有人能够直接获得知识。他们必须依靠宗教领袖、贵族和其他少数人来掌握大部分信息，并根据这些少数人的意愿进行传播。他们自己没办法证实信息是否正确。


实际上，这剥夺了他们的权利——几乎无法证实任何向他们提出的问题——即使理论上他们对政治具有发言权。


这与今天的数据科学有着惊人的相似之处。由于不知道如何质疑数据科学背后的计算结果，无法通过数据科学进行推理，也无法提取信息自己验证，大多数人实际上被剥夺了对其治理做出决策的权利。


这不是一个政党或意识形态的专利。但它的普遍性正在对我们的社会造成越来越大的裂痕，因为人们对实际上控制大多数人生活的数据科学几乎没有共同的认识。计算精英在控制我们的命运方面的能力是强大的，就像几个世纪前文化精英一样。


当然，并不是所有的精英都是恶意的，事实远非如此。但情况要危险得多，因为如此多的权力实际上集中在如此少的人手里，而不诚实的人有能力滥用它。

 


在最近的政治中，我们已经遭遇了一个源于计算的银行业危机和一个由数据科学引发的信任危机。现在几乎没有人相信专家，因为对于大多数人来说，没有教育基础来区分好的和坏的计算论点。预测有着计算和量化的力量加持，却失去了逻辑或现实的基础。人们已经被一些想要通过限制别人的权力来巩固权力的精英所玩弄。

 

如果没有紧急的、重大的干预, 我们最终可能会进入一个新启蒙运动的前夕, 在这个时代, 由于决策和相关思维的关键知识——计算思维——不对称,欺骗能够战胜逻辑思维。每个人都可以获得大量的数据和计算设备, 但只有少数人知道如何从其使用中获得权力。


当普通人的理解能力已经无法支撑对少数人决策权力的约束时, 人们迟早会被误导——越来越严重地被误导。社会缺乏对计算的理解, 可能已经造成了严重的国家安全问题。


我们应该采取什么干预措施？普及计算思维教育。涵盖现代数据科学的教育——不仅包括其计算，还包括原因和相关性、风险和未来预期、如何对数据持怀疑态度、如何计算推理——集中整合的不是过去的现代纸笔技术，而是现在的计算机技术。


陷入前电脑时代的数学教育，除少数精英已经把它发展到一个更高的水平外，离实现这一目标还有很长一段路要走。然而, 它是当今唯一的在学校内能学到计算科目。


长期以来，我一直主张对核心课程进行这样的改变。直到最近我才意识到它的紧迫性。这种紧迫性不仅是为了改善工作、生活富裕, 也是为了保障民众的权益、为了社会凝聚力、为了国家安全。

 

 

关注 哆嗒数学网 每天获得更多数学趣文

原文作者：Wolfram，计算机科学家，数据科学家。

翻译作者，聂海波，哆嗒数学网翻译组成员。

校对：小米、蘇溯

 

 

 关注 哆嗒数学网 每天获得更多数学趣文

终极公理的追求——寻找遗失的真理

 

原文作者：Marianne Freiberger，+Plus网站编辑。

翻译作者，Math001，哆嗒数学网翻译组成员。

校对：小米

 

 关注 哆嗒数学网 每天获得更多数学趣文

 
 
 
 
之所以有那么多人喜欢数学是因为数学给出的答案是确定的。要么真，要么假，真相就像是从基础本源的地方推理出来的。
 
 
 
但事实却是这样的：一直以来，数学其实在一个本不牢固的哲学基础上发展。上世纪30年代，以库尔德·哥德尔为首的一批逻辑学家向大家清楚地展示了数学判定真理的能力是有局限的。他们工作显示，人们完全可以建立很多不同的数学体系。对于一个确定的语句，它们在这些体系里可能是真，可能是假。这取决于对体系的前提预设的偏好。这让数学更像一个游戏，出于我们的需要，我们可以自行选择规则。——再见吧！完美的柏拉图真理观：数学真理是永恒的、独立的。
 
 
但是，也许还有挽救柏拉图主义的余地。在2010年国际数学家大会期间，我们(Plus)采访了数学家武丁(Hugh Woodin)——尽管可能存在大量不同的“数学宇宙”，但这位数学家依然相信人们能选出大家都认为的“最对的那个”。
 
 
数——空集开始
 
武丁是做集合论的，这是数学中非常基础的领域。数学中，集合指一堆事物聚合——至于是些什么事物并不重要。他们可以是一堆数、符号、三角形，抑或我们还可以把这些数、符号、三角形混合起来组成新的集合。我们经常用花括号来表示集合，比如，如果一个集合包含1、2、3三个数，我们就用{1, 2, 3}表示。集合中的对象叫做元素。有一点很重要，一个集合可以是另外一个集合的元素。举个例子，如果你把你购物车购买所有商品的类别看成一个集合，那么你买的一袋橘子就是其中一个元素，而一袋橘子是一堆东西，故本身也是一个集合。
 
 
集合就是一堆事物的聚合。你也许会意外，这个完全无害的集合概念是数学中最本源的基础概念，但结果显示似乎所有的数学对象都能用集合语言描述出来。
 
 
比如自然是0, 1, 2, ... .如果你遇到一个外星人只知道集合，却没有数的概念。你可以一步一步的按如下步骤定义自然数。
 
 
 
0 就是空集。一个没有任何元素的集合。
 
 
 
1就是{0}， 一个只有元素0的集合。(0我们在上一步已经定义好了)
 
 
2 定义成{0, 1}， 一个集合，它的元素是之前定义好的两个对象。
 
 
3 定义成{0, 1, 2}
 
 
以此类推。
 
 
一般的，自然是n定义成集合{0, 1, 2, ..., n-1}，一个包含之前所有定义对象的新集合。
 
 
这种分层式的定义可以很容易地给这些自然数排序，就是说，一个数字我们往后加个一的结果：就是简单地进入下一层级定义的数。自然数和“加一”两个概念就能给出所有算术的定义——因为加法和乘法可以通过不断重复的加一来实现，而减法和除法分别是加法和乘法的逆运算。因此，我们可以只用集合的概念，从空集开始一步一步的建立出自然数的算术体系。而这样的操作表明，所有其他的数学对象，似乎同样都可以从集合构造出来。
 
 
通往无穷之路
 
 
 
也许，集合给予人们最重要的东西就是关于无穷的性质。19世纪末，数学家乔治·康托注意到不需要数数就有办法判断两个集合的元素个数是否相等。你所需要做的事情就是把X中每一个元素和都找一个Y中的元素做匹配，并保证X中没有元素匹配相同Y中的元素。如何你能做到X和Y中都没有剩下没匹配的元素，我们就说两个集合数量一致。或者按数学家的说法：两个集合有相同基数。
 
 
现在，我们取两个无穷集合作例子。N为所有自然数组成的集合，E是所有偶数组成的集合。我们可以做如下匹配（译者注：为了消除误解，添了一个0）：
 
 
 
N 0 1 2 3 … n …
E 0 2 4 6 … 2n …
 
 
 
所以，尽管两个集合都有无穷多元素，其中一个还包含另外一个，我们依然能说这两个集合有相同基数。
 
 
但是，康托同样证明了在自然数和实数之间找不到这样的匹配。实数比自然数“多”，因为无论你怎么找实数与自然数匹配，总有实数会剩下。
 
 
 
这说明存在两种不同的无穷，其中一个无穷大于另外一个无穷。前者，自然数的无穷叫做可数无穷。后者，实数无穷叫做连续统。有个问题是是否有一种无穷“夹在”这个两个无穷之间——这是一个相当复杂的问题，待会儿回来再说。
 
 
康托没止步于这两种无穷，实际上他对所有的无穷都分了层级( hierarchy)，一层一层地，高层的无穷大于低层的无穷。他把这种分出大小的无穷叫做基数，甚至他还设计了基数间做算术的办法。每个基数能衡量有确定性质的无穷集合的元素的多少。
 
从康托的工作开始，数学家开始扩充“无穷陈列馆”中的展品——加入大基数这样怪物。关于无穷的结构呈现出的美妙让数学家们无法抗拒。“有一点最吸引人：我们有不同的办法来描述大基数的层级，”武丁说道，“但是，无论用什么办法，这些大基数都止步于相同的层级。”有更深入的定理表明，一种办法给出的关于无穷的概念的确能被其他的办法描述。这某种程度上说明，关于无穷的层级的相关问题的确是集合论的核心基础内容。
 
 
形式化数学
 
 
从某种程度来说，由于领略到集合的抽象的能力，20世纪初的数学家们都认为他们十分接近一个古老的梦想：把所有数学都建立在一个无懈可击的逻辑基础之上，而且这个基础能被证明没有内在矛盾。这看上去似乎有点奇怪，因为数学本身就是一套最严谨的规则。但是，事实上数学里充满大量的隐藏假设和大量的信仰。就拿我们刚刚的自然数的定义来说，我们就非常隐蔽地假设了，空集是存在的。
 
 
康托意识到实数比自然数多。这只是对无穷层级研究的开始。
 
 
为了精确研究数学中类似的灰色地带，就需要把数学建成为一个形式系统。我们需要事先承认一系列清晰明确且无需证明的命题——我们把这样的命题叫做公理。你还需要明确哪些是合法的推理规则，诸如“如果x=y且y=z,那么x=z”这样。于是，如果一个命题从公理开始可以用合法的推理规则推导出来，那么你就只能认为这个命题是真命题。
 
 
 
集合论看上去就能给这样的形式系统提供完美的工具。貌似所有的数学对象都能被集合语言定义出来，而且集合的概念也足以从相对简单精确的集合公理派生出来。有数学家就适时地做了这样的工作。策梅洛和弗兰克尔把数学建立在八条公理之上，就是数学界熟知的ZF公理。这些公理包含“空集存在”，以及一些看上去非常直观的命题，比如“两个集合相等，当且仅当，两个集合有相同的元素”。现在，最常用的公理除了ZF公理之外，还要加一条更为神秘的公理——选择公理。它们一起组成了ZFC公理。
 
 
 
不完备的数学
 
 
公理化的梦想在上世纪三十年代被无情的击碎了，而完成这一击的就是数学界哥德尔证明的两个数学结果。这就是著名的哥德尔不完备定理：任何一个有能力表述自然数算术的形式系统中，总存在命题在该体系下既不能被证明的为真命题，也不能被证明为假命题。哥德尔再给策梅洛的信中写道：“每个形式系统中，都存在一个在这个系统中可以表述，但从这个系统中的公理出发无法判定真假的命题。”
 
 
于是，ZFC中无法判定真假的命题是什么样的？刚刚我们就遇见一个了。因为康托的提点，我们知道连续统基数比自然数大。那么，命题“两者之间没有别的基数”就成为一个著名猜想，叫做“连续统假设”。现在我们知道，在ZFC公理下，连续统假设是不可证的。它既不真也不假，ZFC无法对这个命题的真假做出判定。
 
 
这太让人意外了，我们曾天真的认为连续统假设应该有个确定的答案。或者说ZFC还不足够强大，需要在ZFC里加入更多的公理？我们甚至可以把连续统假设本身就看成公理——换句话说是不加证明地就把它看成一个真命题。
 
 
但这样做也有问题。首先，哥德尔的结果表明，无论新的系统你加什么样的公理，依旧有无法判定真假的问题。再者，ZFC无法判定的命题还有很多很多，把这些公理都加进去不仅会在系统里产生矛盾，还是一种自欺欺人的表现。
 
 
好了，那么这对数学真理的探索到底意味着什么？“有人提出这样的观点——其实有人已经持有这样观点了——集合论中无处不在的不可判定问题说明，集合论的结论已经超越人类的所有感知，于是这些结果没有任何意义。 那仅仅是受限于人类生理结构产生的结论,”武丁说到，“我觉得那不对，但也很难说。除非我们发现了新的外星文明，看到了他们的数学和我们的数学是否一致。”
 
 
遗失的公理
 
 
不过还有一条不用去寻找外星人的折中道路。现在被接受的集合论公理本身就是人类发明的东西。人们之所以选择这些作为公理，是因为我们“觉得”它们是自然的，它们反映出关于集合以及无穷的概念和我们的直觉一致。也许，存在这个一个公理(或者一系列公理)，能用更直观的方式将这样的直觉补充的更加完备。尽管我们加入了这些公理后，仍然有不可判定问题的存在，但是，也许之前那些在集合论中大量的不可判定问题就可以迎刃而解。“有人可能会说，这就是在玩游戏。你只是为了解决你的问题而去选择把公理加进去。”武丁说，“但也不尽然。最本源的直觉会限制集合论公理的选择。如果你发现一个问题的答案是那些公理的推论的时候，那么这件事情就不仅仅是游戏了。就是说，ZFC公理系统没有能完全反映我们的直觉。”
 
 
回到20世纪30年代，哥德尔本人就加入过这样额外的公理，叫做构造性公理。加入构造性公理的ZFC公理系统能解决包括连续统假设问题在内的一系列不可判定问题。准确地说，哥德尔设计了一种集合类，它满足ZFC体系以及一条额外的性质，后者能把这些不可判定问题变得可判定的。构造性公理保证了哥德尔构造性宇宙中的集合就是世界上所有的集合：带来麻烦的集合是不存在的。
 
 
遗失的公理是什么？
 
 
可惜，哥德尔宇宙种不包含康托设计的大部分关于无穷集合的层级。和连续统假设一样，在原始的ZFC集合论中，大基数的存在性是不可判定的。但是，一但你在ZFC中加入了构造性公理，那么这些不可判定性就消失了：你能证明，这些大基数中的大部分都不存在。很多集合论学家不能接受这个结论：一个公理使得大量的基础基数分层都消失似乎把限制得过头了。林林总总的各种理由下，哥德尔宇宙以及构造性公理的方案被否决。
 
 
但是事情并没有结束。不知从何时开始，武丁和他的同事们开始了对哥德尔宇宙的系统化修正，让修正后的哥德尔宇宙能容纳越来越大的无穷集合。这些工作引领着武丁去构建一个哥德尔集合宇宙的终极形态的概念。这个终极形态能容纳下所有已知的大基数——也许这就是人们遗失的终极公理。武丁心仪的公理能推导出一种非常大基数的存在性，这个基数叫做武丁基数。
 
 
 
 
武丁之所以乐观地认为他走在正确道路上，缘于他们之前的工作的成功。曾几何时，困扰数学家的一些特定领域的核心问题，其实在ZFC下是不可判定的。现在知道，如果所有的集合都满足“射影决定性”的性质，那么这些问题就能解决，但是先验地没人知道为什么所有集合会满足这个性质。表面上看，射影决定性和无穷层级没有什么关系，但是武丁以及他的同事们的工作表明了两者之间的联系。如果你准备接受一条能容纳下武丁基数的公理，那么射影决定性就会顺理成章的成为一条定理。他们同样能证明，如果服从一些通常的结构性的限制，他们给出的公理是能给出射影决定性的唯一公理。
 
 
 
这种看似没有关联的概念之间的却又有深刻的联系，这让用武丁的方法寻找遗失的终极公理增加了更多的可信度。“如果所有这些只是一个人为的制造物，那么我们没有任何理由去期盼这种形式的成果。我们在以我们的基本直觉为基础来寻找公理，目前也没有任何证据让人能相信这个找寻的工作一定能成功。有点像找寻独角兽。我们自认为我们知道独角兽长什么样，但并不意味者我们就能找到独角兽。”如果你的确找到了独角兽，那么你一定正在做一些正确的事情。
 
 
但是，这个工作并不能保证一定能成功。武丁的终极公理能否走通还依赖于一些没有解决问题，这些问题依旧需要有人来给出答案。“现在非常不确定。”武丁承认。“但现在有一系列的猜想在最近两年提出来，如何这些猜想是对的，那么会让集合宇宙的概念趋向统一。如果达成，将解决连续统假设[视其为真]以及其他不可解问题。我认为，现在整个学科处于一个关键的十字路口。”
 
 
 
 
在2010年世界数学家大会上，武丁作出了一个大胆而又富有争议的预言：他寻找的公理将是“一个公认的经得起考验的描述无穷的原理”。但是，他也表示，如果有新的证据诞生，他也并不排除改变自己的想法。就在几年前，他还斩钉截铁的说，根据他当时的工作结果，他笃信连续统假设应该视为假命题。现在，他改变了看法。
 
 
但是武丁能知道到底何时他的公理能正式生效吗？“这不可能说清。有可能就明年，有可能在100年后。我个人只能说，虽然一些猜想看似非常难，但在未来一两年内我们能在上面取得大量进展。现实如此：没人知道一个数学猜想是在明天解决，还是在一千年后解决。”
 
 

关注 哆嗒数学网 每天获得更多数学趣文

神秘数字6174

 

原文作者：西山豊，大阪经济大学教授。

翻译作者，Dr.夏洛克，哆嗒数学网翻译组成员。

校对：333

 

 关注 哆嗒数学网 每天获得更多数学趣文

 

6174是一个相当神秘的数字。乍一看，可能不那么明显。但是正如我们即将看到的，任何一个会做减法运算的人都能发现使得6174如此特别的秘密。

 

 

卡普雷卡运算

 

1949年来自印度的数学家卡普雷卡(D.R.Kaprekar)引入了一个今天被称为卡普雷卡运算的步骤。首先选一个各位数字不全相同四位数（也就是除了1111,2222，。。。）。然后重排各位上的数字得到这些数字能组成的最大与最小数。最后，从最大的数中减去最小的数得到一个新的数，接下来对每一个新的数重复以上运算。

 

 

这是一个简单的运算，但是卡普雷卡得出一个惊人的结果。让我们试一下，以数字2005开始，也就是去年年份的各位数。用这个数的各位数字我们得到最大数是5200，最小数是0025或者25（如果有一个或者一个以上的数字是0，把他们放在最小数的左边）。减法如下：

 

5200 - 0025 = 5175
7551 - 1557 = 5994
9954 - 4599 = 5355
5553 - 3555 = 1998
9981 - 1899 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174
7641 - 1467 = 6174

当我们得到6174时，运算开始重复，每次都得出6174.我们称6174是这个运算的一个核。那么6174是卡普雷卡运算的一个核，但是这是不是想得到6174那样特殊呢？也就是说不止这个运算只有6174一个核心，溯流而上它还有另一个惊喜。让我们用一个不同的数再试一下，比如说1789.

 

9871 - 1789 = 8082
8820 - 0288 = 8532
8532 - 2358 = 6174

 

我们又得到了6174！

 

当我们用2005开始时，7步得到了6174，然而对于1789用了3步。实际上，所有各位不全相同的的四位数你都能得到6174.太牛了，不是吗？卡普雷卡运算如此简单但是揭示出一个如此有趣的结果。当我们思考所有四位数都能得到这个神秘数字6174的原因时，这会变得更加引人遐思。

 

只有6174吗？

 

任意一个四位数通过降序排列各位数字都能得到一个最大数，通过升序排列得到最小数字。那么对于四个数字a，b，c，d，其中

9 ≥ a ≥ b ≥ c ≥ d ≥ 0

同时a，b，c，d不全相同，最大数是abcd最小数是dcba。

 

对这个问题的每一列用标准的减法运算就能算出卡普雷卡运算的结果：

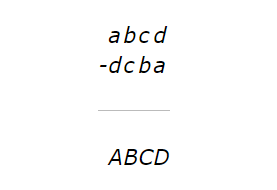
得出如下关系：

D = 10 + d - a (a > d)

C = 10 + c - 1 - b = 9 + c - b ( b > c - 1)

B = b - 1 - c ( b > c)

A = a - d
 

 

这些数字中a>b>c>d.

 

如果结果数字可以用原始的四个数a，b，c和d写出，卡普雷卡运算就会重复。那么通过考虑所有可能的组合{a，b，c，d}并检验它们是否满足上述关系，就能找到Kaprekar运算的核。对a，b，c和d的4！=24种组合的每一个组合给出一个含有四个未知数与四个等式的方程组，那么我们应该能从这个方程组中解出a,b,c,d。 

 

结果，这些组合中只有一个组合有整数解且满足9 ≥ a ≥ b ≥ c ≥ d ≥ 0。这个组合是 ABCD = bdac，此时相应的方程组的解为 a=7, b=6, c=4 and d=1。也就是 ABCD= 6174。 整数 {a,b,c,d}  中某些数相同时没有使等式同时成立的有效解。因此，6174是唯一一个不会被卡普雷卡运算改变的数——我们的神秘数字是唯一的。

 

对于三位数会出现相同的现象。比如把Kaprekar运算应用在三位数753上，产生如下结果：

753 - 357 = 396
963 - 369 = 594
954 - 459 = 495
954 - 459 = 495

数字495是三位数运算（卡普雷卡运算）的唯一核，也就是用这个运算时所有的三位数都会得到495.为什么你不自己检验一下呢？

 

得到6174要几步？

 

从我朋友那里第一次听说6174是在1975年，当时我印象很深刻。当时我认为很容易证明为什么这种现象会出现，但是事实上我没能找到原因。我曾用电脑检验是否所有的四位数在有限步运算内都能得到核6174。这个大约50行的visualbasic程序检验了从1000到9999各位不全相等的所有8891个四位数。

 

下面的表格显示了结果：每一个各位不全相等的四位数在卡普雷卡运算下都得到了6174，而且都在7步之内。如果使用卡普雷卡运算7次之后没有得到6174，那么你就在你的计算中犯了错误，要重新试一下。

 

Iteration

Frequency

0

1

1

356

2

519

3

2124

4

1124

5

1379

6

1508

7

1980
 

 

 

怎样得到6174？

 

当研究卡普雷卡运算时，我的电脑程序检验了所有的8991个数，但是在Malcolm Lines的文章中说只需要检查所有可能四位数中的30个就足够了。

 

让我们计算过程中的第一个减法。最大数是1000a+100b+10c+d 最小数是 1000d+100c+10b+a。那么减法是：

 

1000a + 100b + 10c + d - (1000d + 100c + 10b + a)
= 1000(a-d) + 100(b-c) + 10(c-b) + (d-a)
= 999(a-d) + 90(b-c)

 

 

 (a-d) 的可能值是从1到9， (b-c) 的可能值是从0到9.通过遍历所有可能，我们能看到运算过程中第一个减法运算的所有可能结果。这些结果显示在表格1中。

 

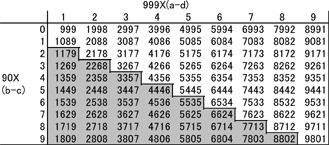
表1：Kaprekar运算的第一个减法后产生的数

 

我们只对各位数不全相等且a ≥ b ≥ c ≥ d的数有兴趣，因此我们只需要考虑那些 (a-d) ≥ (b-c)的数即可。那么我们就可以忽略表1中的灰色区域，这个区域包含(a-d) < (b-c)的数。现在我们把表中数的各位数字降序排列，得到第二个减法运算的最大数：

 

 

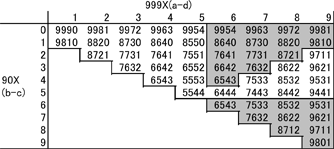
表2：第二个减法备用的最大数

 

我们可以忽略表2中的重复数字（灰色区域），于是仅剩余30个数字进行接下来的处理。下图展示了这些数字变成6174的路线。

 

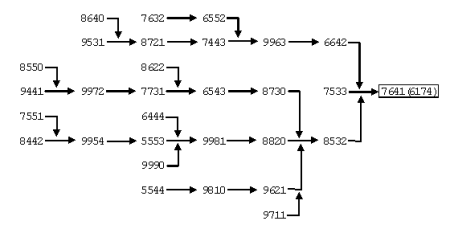
这30个数如何变成6174的

 

在这个图你能看到所有的四位数都在最多7步之后得到6174.即便如此我依然认为它很神奇。我猜发现这个数的卡普雷卡要么是极其聪明要么是有很多时间思考这个运算。

 

 

2位数，5位数6位和更多位的数……

 

 

我们已经看到四位数和三位数都得到唯一核，那么其他数呢？结果答案不那么印象深刻。让我们试一下一个2位整数，比如说28：

82 - 28 = 54
54 - 45 =   9
90 - 09 = 81
81 - 18 = 63
63 - 36 = 27
72 - 27 = 45
54 - 45 =   9

 

不难验证所有的两位数都将得到9→81→63→27→45→9的循环。不像三位数和四位数，2位数没有唯一核。

 

那么5位数呢？5位数会有一个像6174和495那样的核吗？为了回答这个问题，我们需要使用一个像之前的过程：检验 {a,b,c,d,e} 的120个组合ABCD满足

9 ≥ a ≥ b ≥ c ≥ d ≥ e ≥ 0

和

abcde - edcba = ABCDE.

 

 

万幸计算机已经完成了计算，而且众所周知5位数没有卡普雷卡运算核。但是所有的5位数确实都得到如下三个循环之一：

 

71973→83952→74943→62964→71973
75933→63954→61974→82962→75933
59994→53955→59994

 

正如Malcolm Lines在他的文章中指出的那样，检验6位或更多位数会发生什么会很费时间，而且这项工作会变得相当无聊！为了使你免于这种命运，下表展示了2位数到10位数的核。图表显示卡普雷卡运算只能把所有3位和4位数变成唯一核。

Digits

Kernel

2

None

3

495

4

6174

5

None

6

549945, 631764

7

None

8

63317664, 97508421

9

554999445, 864197532

10

  6333176664, 9753086421, 9975084201

 

 
 

 

漂亮吧，那它有那么特殊吗？

 

 

我们都看到在卡普雷卡运算下所有的三位数都得到495所有的四位数都得到6174.但是我没能解释为什么这样的数能得到唯一核。这是一个偶然现象还是发生这些的原因有更深的数学原理？（原理）就像结果一样既漂亮又神奇，这可能只是一个巧合。

 

让我们听一下看一个日本人山本幸雄的漂亮谜题。

 

如果你把两个5位数相乘能得到123456789.你能猜到这两个5位数吗？

 

 

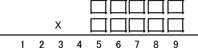
这是一个非常漂亮的谜题，那么你可能认为它背后应该藏着一个很大的数学理论。但是实际上它的美只是一个偶然，也有其他相似但是不那么漂亮的例子。比如：

 

 

 

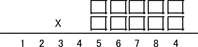
看到幸雄的谜题，你可能就跃跃欲试想要解出它，因为它是如此美丽，但是如果我给你第二个谜题你可能就一点都不感兴趣。我认为卡普雷卡问题就像幸雄的数字谜题一样。我们被他们吸引都是因为它们是如此美丽。因为它们如此美丽我们觉得它们有更多的内容，事实上他们的美丽很可能是偶然的。过去这样的误解也导致了数学和科学的进步。

 

 

只知道卡普雷卡运算下所有的四位数都得到6174但是不知道原因够吗？至今为止，没有人能说所有的3位和4位数得到一个唯一核是一个偶然现象。这种属性看起来这么惊人使得我们期待着它背后隐藏着数论定理。如果我们能回答这个问题，我们可能发现这只是一个美丽的误会，但是我们希望不是。

 

 

参考书目：

 

Kaprekar, D. R., "Another Solitaire Game", Scripta Mathematica, vol 15, pp 244-245 (1949)

Gardner, Martin, "The Magic Numbers of Doctor Matrix", Japanese version, Tokyo: Kinokuniya (1978)

Lines, Malcolm E., A number for your thoughts: facts and speculations about numbers..., Bristol: Hilger (1986)

Nishiyama, Yutaka, Kurashi no Algorithm, Kyoto: Nakanishiya (1993) 

 

 

关注 哆嗒数学网 每天获得更多数学趣文