为什么R² = 0.99不一定是好消息?
原文作者:Gary Ernest Davis
译文作者:我是崔小白,哆嗒数学网翻译组成员。
校对:333
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
在经济、政治科学和心理学等社会科学领域中,人们普遍认为R = 0.7在线性回归的结果中是值得庆贺的。
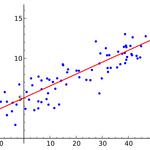
R2 反映了因变量的全部变化能通过回归关系被自变量充分解释的比例,然而对于R = 0.7,这个比例大约是50%。
在物理学中,因变量和自变量需要更高的线性拟合度,所以在物理学期刊中,如果R2的值如果小于0.95则认为研究结果是十分不可靠的。
如果我们线性回归中的r2 =0.99说明总体结果良好,对吗?我们可以确定一定以及肯定,因为在因变量的变化中只有1%不能由自变量的变化来解释的。
其实那可不一定,可以用如下简单的例子来解释。
生物学的一个案例
支原体细菌有一个包含580076个核苷酸的基因组。在该基因组中,起始密码子ATG出现了9,020次,并且这些ATG密码子开始和结束的位置为214, 263, 355, 452, 467, 547, 568, 686, 734, 822, 831, 850, 930, 1023, … , 579349, 579358, 579437, 579508, 579579, 579717, 579804, 579846, 579889, 579892, 579927, 579961, 580026, 580042。我们可能会问的一个问题是:这些ATG密码子的位置是否均匀分布在基因组上?
解决这个问题的一个非常简单的方法是,在1到580,076的范围内,产生9020个均匀分布的随机整数,并以这些随机整数为自变量绘制出ATG密码子位置的散点图。换句话说,通过线性回归,我们来看ATG位置的变化有多少是可以由均匀随机整数变量的变化来解释的。
(熟悉线性回归的读者可能会认为这并不是一个好主意,因为这里的自变量是服从均匀分布的,而不是正态分布——这是线性回归的基本假设之一。)
下面这幅图描绘的是ATG密码子的位置比照从小到大排列的9020个均匀分布随机整数的散点图:
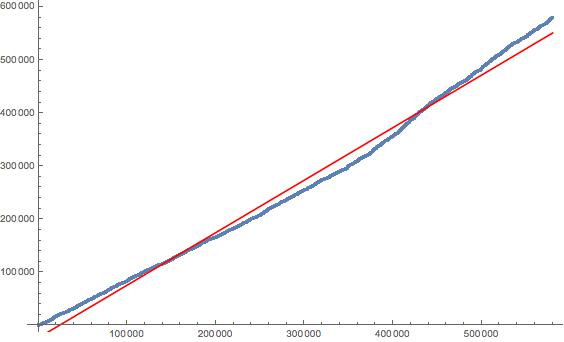
数据点的位置––ATG比照有序的随机整数–是蓝色的线表示,而回归线由红色的线表示。
对于这个回归得到r2 = 0.9912,这表明ATG密码子位置的变化只有小于1%的比例不能由自变量,即这里的随机整数的变化所反映。
然而,这幅图还告诉了我们一些别的东西:数据点先是在回归线的上方,然后落到回归线以下,接着又回到了回归线上方。
更为仔细的观察
我们可以更清楚地了解数据点和回归线之间的差异–残差–通过观察残差图:
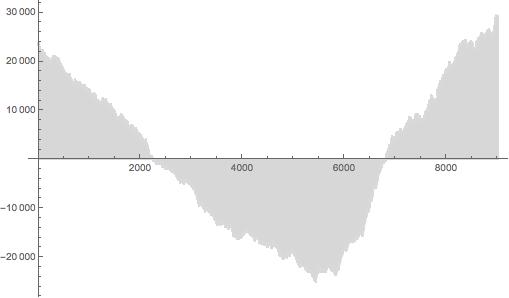
也许这只是一个从1到9020的特定随机选择的产物?
为了测试这个问题,我们可以多次重复我们的随机选择。当我们这样做的时候,发现这种模式仍然存在:在支原体基因组中,ATG密码子的位置和1至9020的有序随机整数之间存在很小但真实存在的差异。
基因组中的ATG密码子位置和随机位置是一个很小的但也可能很显著的差异。
作为一个生物学家,你不想深入研究一下吗?
得到的启示?
警惕“高”的R2 值:仔细地观察回归中的残差图,并试图理解这个图背后的含义。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

评论已关闭