有图有真相：以为了解JPG图，你太天真！

 

原文作者，David Austin，大峡谷州立大学。

翻译作者，小涟猫，哆嗒数学网翻译组成员。

校对，333。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

下面这张图片以矩阵形式包含了3871488个像素。每个像素的颜色由红绿蓝分量决定，每种颜色占一字节内存，我们可能想当然地认为，这个图片会占11614464字节内存，但是这个JPEG 文件实际只占734268字节内存，约为原来十六分之一。下面我们将会介绍这种由联合图像专家小组（JPEG）开发的高效图像压缩算法。

 

 

相比专门使用红绿蓝三种颜色分量，用另外三种不同的分量来描述会更方便:亮度Y, 与颜色明亮程度密切相关；C_b、C_r为蓝色、红色色度分量，它们可以粗略地确定一个色彩。上述两种表示方法可以通过一个可逆的仿射变换实现相互转换。例如，为重新获得红、绿、蓝分量的值，我们可以用以下公式：

可以看出，亮度与三种基本颜色分量的作用相同。为了可视化这个变换，我们保持亮度不变并且混合各类色度值得到以下颜色

 

 

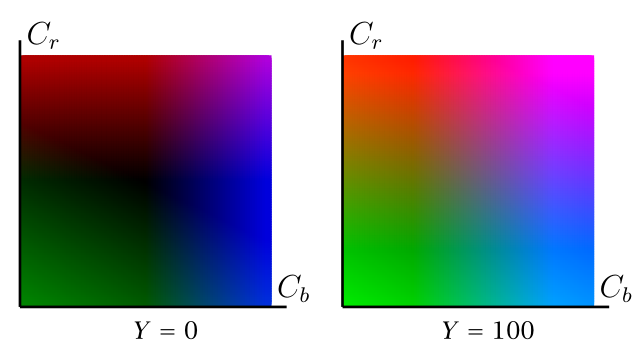
这个算法将图片分割为8*8的可单独处理的图像块，这是一个样本模块。

在我们的样本模块中，（Y，C_b，C_r）三种分量的分布情况如下，明亮的区域对应更大的数值。

可以看出亮度值Y产生的是原图的灰度图。心理可视化实验表明，人眼对亮度变化最为敏感，因此对颜色转换时可以把最重要的信息压缩到单个分量中。彩电使用相似的颜色模型，它能让黑白电视也可以有效播放貌似彩色效果的图像。

 

原因稍后解释，现在我们用一些频率越来越块的余弦函数的线性组合求表示各个分量值。例如，如果Y_ x,y 代表图像块中的第x 行，第y 列的方块处的亮度，就可以表示为

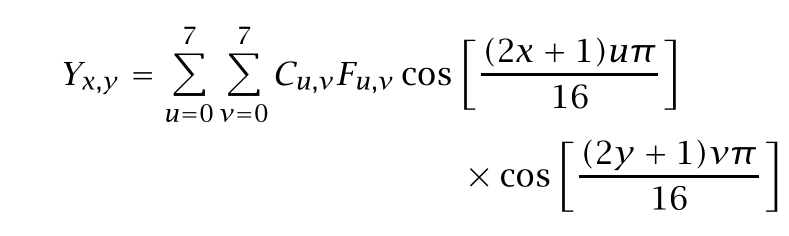
归一化常数C_u,v 不需过分关注; 系数F_u,v由二维离散余弦变换（DCT）得到，而对于它的高效计算则可以采用快速傅立叶变换（FFT）。

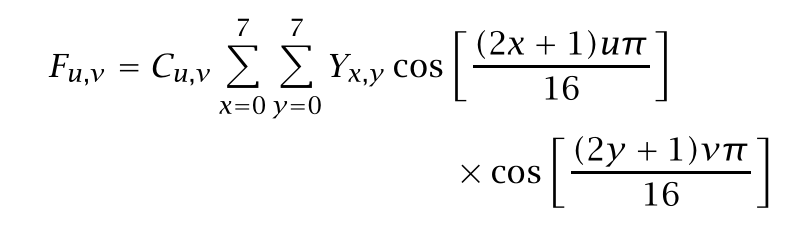
大多数图像块的分量值不会急剧改变，人眼对这些变化也不是很敏感，因此，频率较高的DCT 变换系数可能很小甚至忽略也不影响对我们对于图像的感知。这样的观察启迪了我们，也许可以以整数的形式来量化DCT的系数并加以存储。

 

量化过程涉及两个要素。第一个为参数α，它由使用者选择，用于控制压缩程度与图片质量。α值越大，文件越小，图片质量也就越差。

 

第二个因素是一个8*8的矩阵Q=[Q_u,v]，其中的系数为对F_u,v /αQ_u,v取整后的值, 依经验选取Qu,v时，为了弱化高频的影响，通常对于高频部分赋予较大的数值。例如，一个用于量化亮度离DCT系数的矩阵为

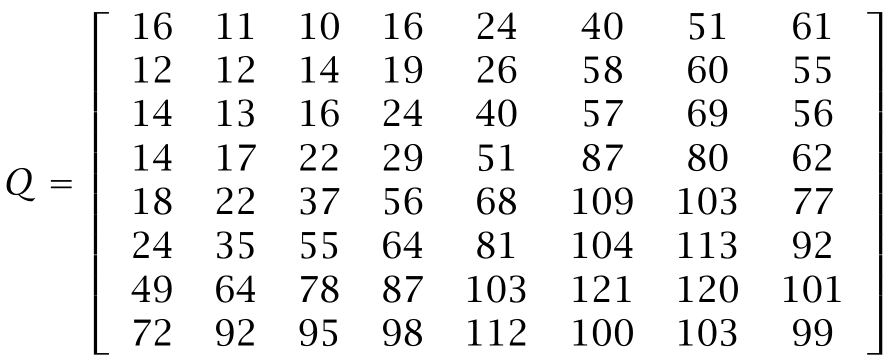
考虑到亮度携带更多重要的视觉信息，所以我们用不同的矩阵来分别量化描述亮度的系数与描述色调的系数。用中间值α处理我们的样本图像块，量化后的亮度系数如下

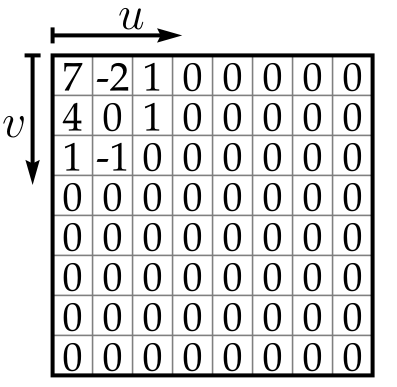
量化后的系数按照箭头指向排序，低频排在前面。

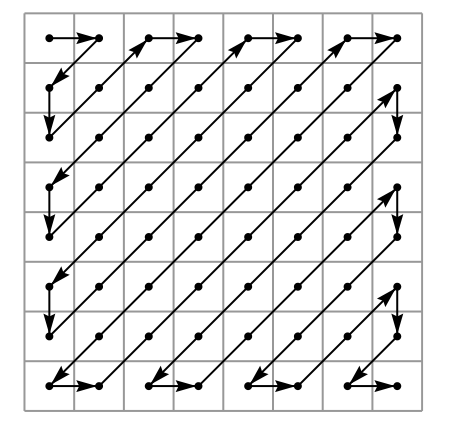
样本的亮度分量，其量化后的系数为数列 7, -2, 4, 1, 0, 1, 0, 1, -1以及55个0。相比存储这么多数字零，我们直接记录零的个数，这样极大减少了存储需求。后续的压缩要依靠哈夫曼编码来实现系数数列的高效效存储。

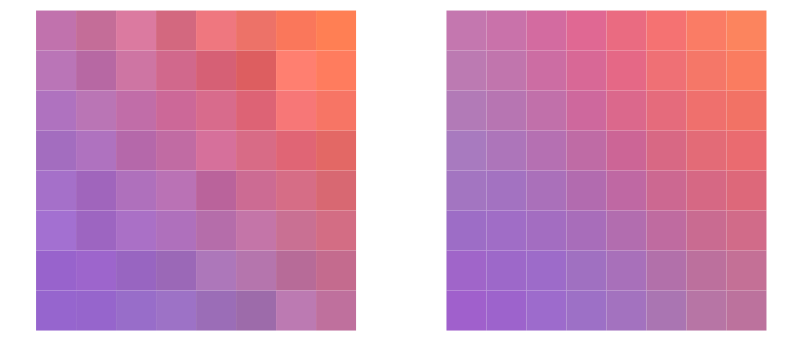
图像的重建可以通过逆过程实现。量化系数给出了F_u,v的近似值，这些反过来又给出了Y, C_b , C_r和R,G,B 分量的值。下图中左图表示原图，右边则是重建后的图。

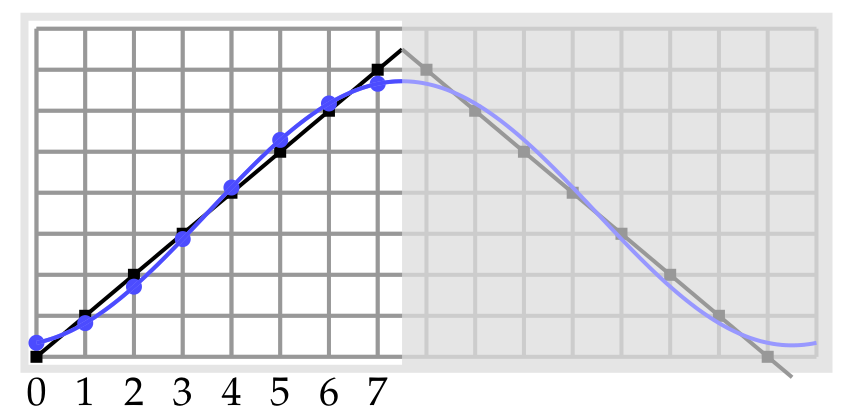
DFT似乎比DCT 更好用，因为它易于计算。但是我们却选择了DCT，这是因为我们希望把信息尽量集中到频率较低的系数上。以8*8模块中的某一行Y_x的值为例, DFT方法将Y_x表示为一些周期为8的函数的线性组合，并由此给出了Y_x的一个周期延拓。但该变换非常不必要地将 y_7 与 y_8 = y_0之间的变化也记录下来了，这就导致了高频分量的加入以及由此产生的显著影响。在下面的图中，Y_x 值用黑色表示，而由傅立叶变换的三个最低频项所给出的近似值是用红色表示的。

   
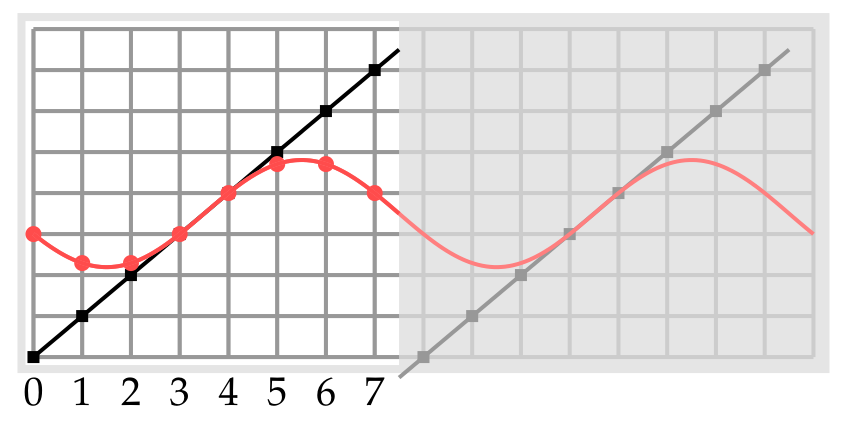
   与之相比，DCT方法将Yx表示为一些周期为16且关于x=7.5对称的函数的线性组合。这使得Y_x的近似延拓更为平滑，从而减少了对高频分量的依赖。下图是DCT所给出的近似值，注意到近似效果得到了显著改善。

因为这些8*8图像块都是被独立处理，所以这就导致了在高压缩率的情况下边缘部分的不连续性变得十分明显。除此之外，我们通常还希望用中等分辨率就能高效重建图像。这些因素以及一些其他原因，促使了JPEG2000压缩算法的产生。在诸多不同点中，JPEG2000还采用离散小波变换代替了DCT

JPEG2000算法把图像分割为尺寸更加精细的图像块，比如256*256。为了演示小波变换，取图像块中的一行像素并令y_x 代表该行中的某一个值。现在求小波系数。

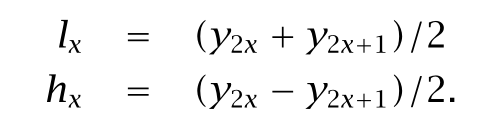
h_x为能够检测到高频变化的高通系数，l_x为低通系数。按照低通系数在前高通系数在后的顺序进行排序，对列也做相同处理后，可得小波系数的数表。

   
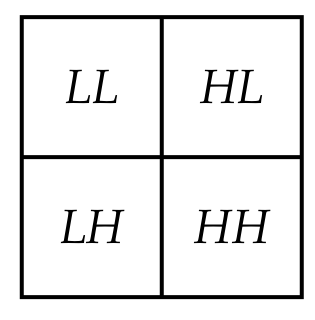
位于LL子块中的系数是通过对所有2*2的邻近像素点取平均值得到的因此代表了一个低分辨率的图像。另外三个子块描述了当重建高分辨率图像时所必要的变换。我们对LL子块重复之前的处理，从而实现以越来越低的分辨率存储图像。

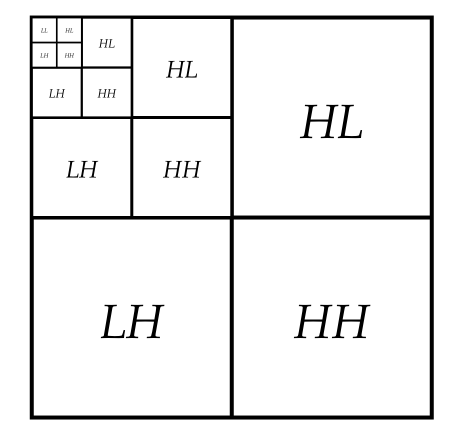
量化的过程会检测数值变化不明显的区域，从而可以安全地忽略高通系数。和之前介绍的小波变换求取两个相邻值的平均值不同的是，JPEG2000算法使用Cohen-Daubechies Feauveau (9, 7) 小波变换，它可实现取邻近九个值的平均值，这样可令图像更加平滑。

 

JPEG2000的算法复杂度比JPEG高一个数量级，而且在中、低压缩率时，图像质量并没有优化多少。但是在高压缩率情况下，JPEG算法采用的8*8图像块会导致图片质量严重下降，而JPEG2000的效果此时会明显更好。

因为JPEG2000在获取同等质量图像时更为费劲，所以它对JPEG来说并没有明显优势。事实上，目前只有少数网站支持显示JPEG2000图像。它的优势在于，当处于增加算法复杂度不再是问题的环境下，可以为图像提供灵活的格式。

例如利用小波变换能以不同分辨率有效重组图像，用户可肉眼迅速大量搜索低分辨率的图片。JPEG2000允许用户指定区域以高分辨率展示，通常是出于医学成像的需要。最后，它也使得数码图像能以JPEG2000的格式存储在相机内存卡中，这样在拍照后，图片会以低分辨率存储起来以减少内存使用。在JPEG面世约十年后，JPEG2000才出现。它还拥有一些其他的功能特性，比如事后图像加密的功能。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa