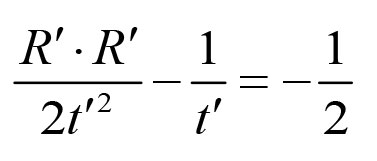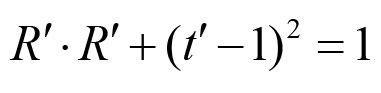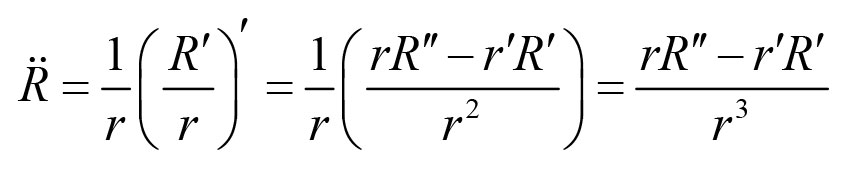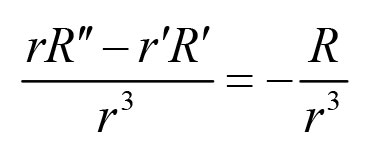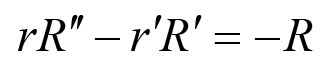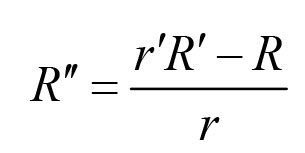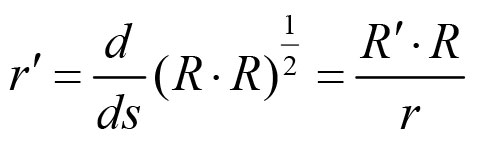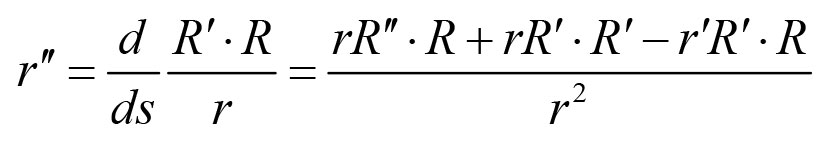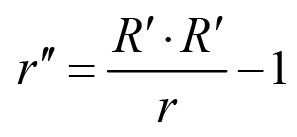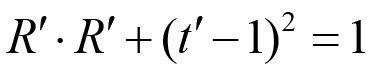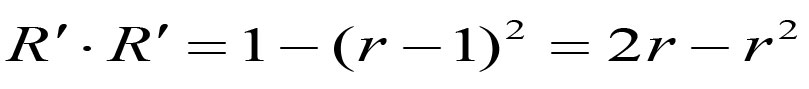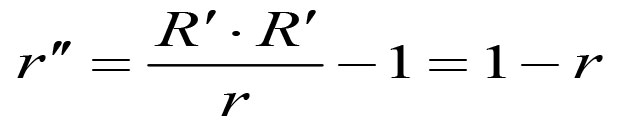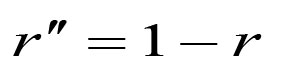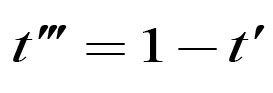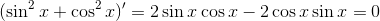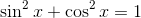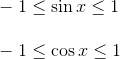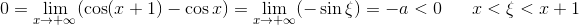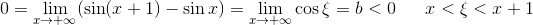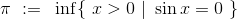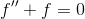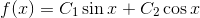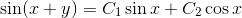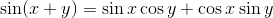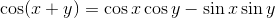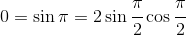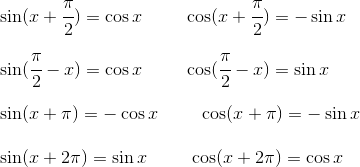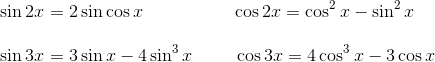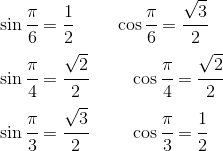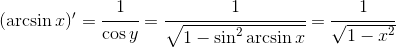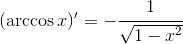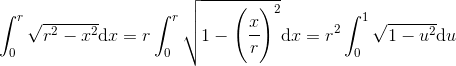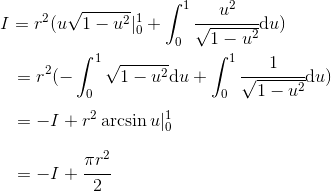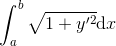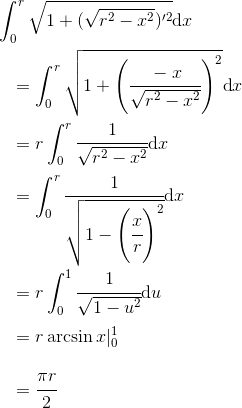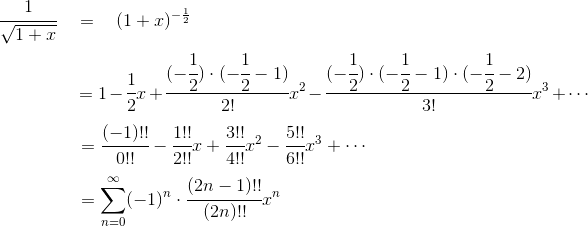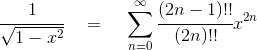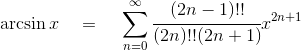作者：欧阳顺湘，本文转自其公众号和乐数学（kelemath）
关注微信：哆嗒数学网 每天获得更多数学趣文
新浪微博：http://weibo.com/duodaa
摘要：本文从2017年11月开园的深圳人才公园上π桥上的众多错误和值得商榷处谈起，分析原因，指出部分错误同样出在有影响力的作者的数学普及读物中；同时以著名作家数学作品中的不足以说明错误的普遍存在性，呼吁批评家勇于担当，作家珍惜其影响力，社会重视数学普及。
2017年11月1日是深圳市立法确认的首个“人才日”。这一天，深圳人才公园正式开放。该公园是全国首个以人才为主题的公园，体现了深圳市对人才的重视。
公园不但风景秀丽，也独具科学与数学文化精神，如园中的最美公式长廊和π桥，就是这种精神的具体体现。π桥两侧的栏杆上铺了圆周率小数点后2017位的近似数字，同时桥栏杆的众多挡板上以简短的文字介绍了圆周率的历史和相关趣闻。可以设想，π桥将与北京珠市口大街上装饰了拉格朗日公式、爱因斯坦质能方程两个著名公式的天桥南北呼应。
圆周率的历史是人类文明之境。展示π的历史，不但要介绍人类文明所取得的璀璨成就，也一定会介绍我国古代数学家取得过的杰出成就。这样可使公众了解我国古代数学家的智慧，增强民族骄傲感，坚定文化自信。
这样一座小桥，相当于一个可以寓教于游乐的科普小展馆，其设计思路值得点赞。然而，近日笔者经过参观，遗憾地发现π桥上多处事实错误和有待商榷处。
公共空间中各种翻译、拼写错误其实比比皆是，没必要小题大做。但在人才公园这样彰显理念的重要地方，出现错误，值得反思；考虑到错误产生的原因，更值得引起重视。
1 π桥上的错误和意义不明有待商榷处
我们先指出桥上的问题，供人才公园做修改参考。
1.1 明显错误
桥上至少有4处明显错误。
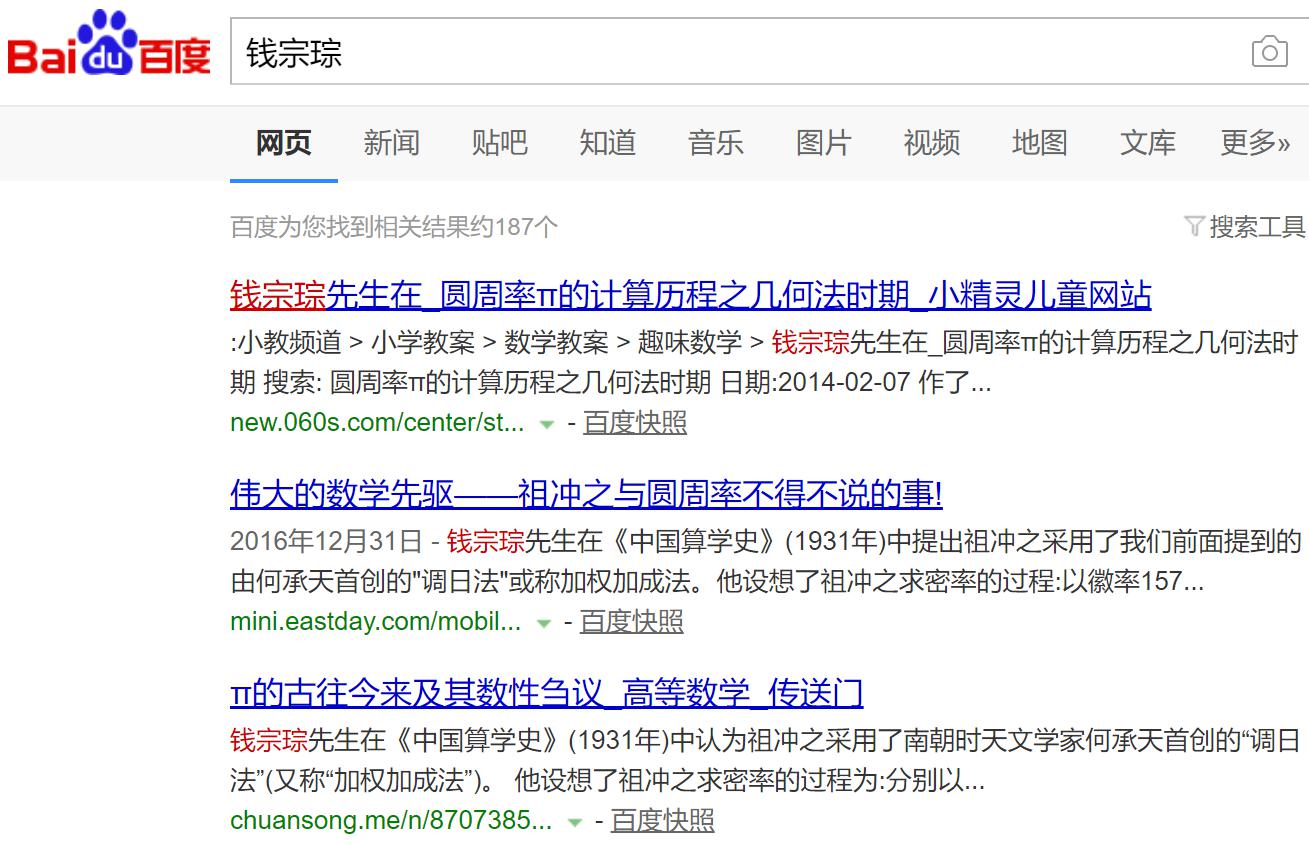
1.钱宗琮先生在《中国算学史》中提出……
这里把我国著名数学史家钱宝琮先生的名字写错了。
2.“我国魏晋时期数学家刘徽所著的《九章算术》……”
刘徽是给《九章算术》作注，即阐释、发扬并补充，并不是著。
3.1965年，英国数学家约翰·沃利斯推导出一个公式，，发现圆周率等于有规律的无穷个分数相乘的积。
这个发现实际上是1655年得到的。时间相差了近300年。
4.2015年，在“最强大脑”节目上，73岁的吕老先生成功挑战记忆π值小数点后5000位……。
实际上，这位老人姓吴，叫吴光仁。
1.2 意义不明和有待商榷处
还有些说法有误或意义不明，容易误导不明真相的读者。
1.“人才栈道巧妙地利用圆周率无穷尽的特点，以不重复的数字，铺满长约150米的桥体栏杆，栏杆上π的位数为小数点后2017位……”
这里应该将“不重复”改为“不循环”。数的十进制表示用到10个数字，要表示圆周率小数点后2017位，不得不重复。人们已经证明π是无理数，所以是无限不循环小数。全桥共有两处类似错误介绍。
2.“1596年，荷兰数学家卢道夫” “德国数学家科伊伦”
这是两条记录中的用词，实际指的同是生于德国的荷兰数学家Ludolph van Ceulen。如此叙述，容易误导游客。
3.（钱宝琮）提出祖冲之计算圆周率采用的何承天首创的“调日法”：“冲之在承天后，用其术以造密率，亦意中事耳。”
这段话不清晰，易使人以为钱宝琮也提出了“调日法”。这里的本意应为：祖冲之计算圆周率的方法已经失传，但钱宝琮提出，祖冲之可能采用了何承天的“调日法”。
4.直到19世纪初，求圆周率的值应该说是数学中的头号难题。
实际上，牛顿和莱布尼兹在17世纪后半叶创立微积分之时，各自都发现了不同的用无穷级数计算圆周率的方法，圆周率的计算已经不再神秘，也不是数学中的头号难题，甚至不是主流问题。说成头号难题是引人瞩目的噱头。
当然，如果一定要这样说，也可以，即使是现在，要轻易地算出很多位，也需要计算能力和好的算法。以此，这个说法最多算一家之言，不是共识。类似于“直到19世纪初，求圆周率的值应该说是数学中的头号难题”这样值得商榷之处，在桥上还有其他处。
5.刘歆通过做实验，在制造标准容器的过程中就用到了圆周率的值。
这段话莫名其妙。实际意思应该是说，刘歆为了制造标准容器“嘉量”，需要用到圆周率的值。他（可能）是通过实验的方法得到圆周率的值的。
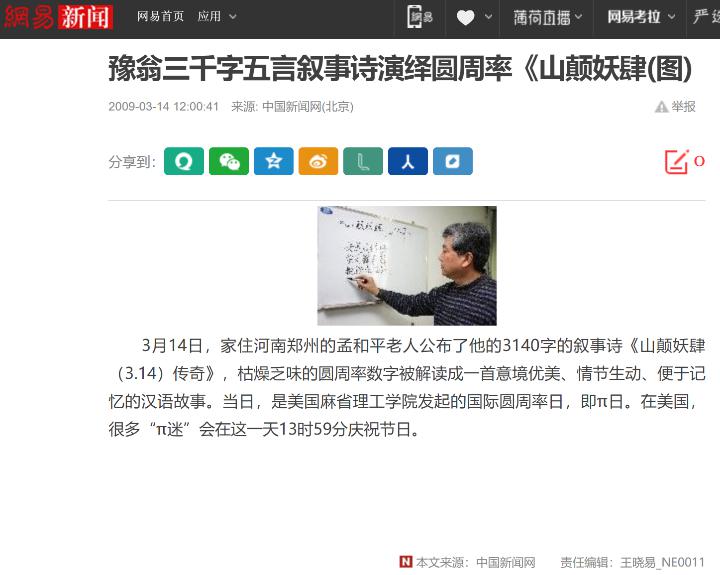
6.我国河南郑州的孟和平老人写了一首3140字的叙事诗《山巅妖肆（3.14）传奇》。一首意境优美、情节生动，便于记忆的爱情长诗。
这里所谓的长诗，是利用谐音牵强附会地编的一个故事。且不说是否有意义，内容和文字都不好：
1.内容很无聊。故事说的是山顶的酒肆里有九位相貌妖艳的舞女，她们因为一些小事不欢而散，各奔东西，后来又相聚在另一家酒肆里，最终不计前嫌，一同开怀畅饮。
2.文字算不上诗，诘屈聱牙。且看前面几句：要是要我酒（14159），尔乐舞扇舞。把酒吃酒散，尔散拔四柳。（要是想要我的酒，你得跳段扇子舞。举杯把酒喝完后，还得拔四棵柳树。）
“意境优美、情节生动，便于记忆的爱情长诗”这样的词句只能用来形容《长恨歌》《琵琶行》《春江花月夜》。
在一座不长的桥上，出现如此之多的错误和值得讨论的地方，对希望起寓教于乐之功能，并体现人才意识的这样一座桥来说，不免有煞公园优美的风景，不免有愧于公园的人才主题。
2 错误是怎样产生的呢
设计者没能认真仔细对待，没有意识到参考的资料可能有问题，需要咨询相关专家，自然难辞其咎。但设计师一定参考了数学工作者的相关作品。
通过网络搜索，不难发现，有的错误是设计者一知半解地修改一些知识导致的；有的是以讹传讹导致的。在现在自媒体旺盛，传播途径快速方便的情况下，错误跑得比光都快。
我们以前面指出的问题中的两处为例来说明。
2.1 韩雪涛的文章《圆周率π的计算历程》
钱宝琮先生的名字被写错，一开始可能原因是输入失误，或将“宝”的繁体字“寶”看成“宗”字等。但可以肯定的是，不少人都是以讹传讹。
搜索钱宝琮的名字的误写“钱宗琮”，可发现这竟然是网络上很常见的错误，百度搜索有187个结果。
例如，号称最大手机电子书平台上“掌阅”上有的一本名为《数学趣闻》的书中就有这样的错误。（http://www.ireader.com/index.php?ca=Chapter.Index&bid=10098064）
韩雪涛的一篇文章《圆周率π的计算历程》中也把钱宝琮先生的名字写成了“钱宗琮”。
韩雪涛是知名数学普及图书作者，很快可以查到他编写有7本图书：
1.从惊讶到思考 : 数学的印迹，长沙 : 湖南科学技术出版社 ,2007
2.从惊讶到思考 : 数学悖论奇景，长沙 : 湖南科学技术出版社 ,2007
3.好的数学 : “下金蛋”的数学问题，长沙 : 湖南科学技术出版社 ,2009
4.好的数学 : 数的故事，长沙 : 湖南科学技术出版社 ,2014
5.好的数学 : 方程的故事，长沙 : 湖南科学技术出版社 ,2012
6.（王元 [(1930.4-)] ;学夫子 ;韩雪涛 ;田廷彦）改变世界的科学. 数学的足迹，上海 : 上海科技教育出版社 ,2015
7.数学悖论与三次数学危机，长沙 : 湖南科学技术出版社 ,2006
韩雪涛曾参编《十万个为什么》（第六卷，数学）。他与王元院士等合编的《改变世界的科学——数学的足迹》曾获第四届“中国科普作家协会优秀科普作品奖” 金奖。
据韩雪涛先生介绍：2000年左右，他完成了《数的故事》的书稿，把书中介绍圆周率计算的部分摘出来，投给当时的《三思科学》电子杂志，发在《三思科学》电子杂志（2002年第12期·2003年第1期），之后这篇网文就在网络上广泛流传。前几年正式出版的《好的数学--数的故事》一书中也错了。（感谢韩先生的回复）
韩雪涛先生的这篇文章流传很广（可见网络媒体的力量），各处转载，如：
1.博客转载：
https://blog.csdn.net/xjwyb/article/details/322994，
2.360图书馆收藏：
http://www.360doc.com/content/11/1007/21/38416_154157472.shtml
3.道客巴巴：
http://www.doc88.com/p-909591547279.html
4.微信公众号平台转载，如曾经颇有名气和影响力的微信公众号的“赛先生”在2016年9月18日转载过此文： https://mp.weixin.qq.com/s/dK6XJ310-jB7Zx6bMNfOpw 。
我们前面提到的π桥上一个值得商讨的说法——“直到19世纪初，求圆周率的值应该说是数学中的头号难题”——在网络上也是很流行；韩雪涛作的《圆周率π的计算历程》也持这个说法。据韩先生介绍，他的第一反应是他不会写这样的一句话；虽然初稿和网文中有这样一句，但出版的书中删掉了。
2.2 科学精神的缺失与《说不尽的圆周率》
郑州老人用谐音编“诗”的 “新闻”从2006年开始，即在网络上以各种形式不断出现。我们质疑的是π桥对此“诗”的赞扬是无视事实的。
不知道设计者是怎样想到加入这样一句的，可能是觉得是一个趣闻，有如有人根据圆周率普的曲一样有趣，可惜的是设计者审美太差或没有去读。不论如何，将一则雅俗共赏都谈不上的花边新闻放到π桥上，并对一首内容恶俗的所谓的诗大加赞扬，也是没有科学精神。这位闲着无事的老人的名字完全不应该与π桥上众多为数学做出杰出贡献的名人的名字并列。
当然，设计者也可能是受网络消息或数学书的影响。
2016年人民邮电出版社出版的科普书《说不尽的圆周率》第191页也抄录了类似的“赞词”：“河南郑州的一位老人……把枯燥乏味的数字解读成一首意境优美、情节生动、便于记忆的汉语故事。”
《说不尽的圆周率》的作者陈仕达、陈雪都是中学老师，编写了很多数学普及图书，特别是共同参编的《说不尽的π》与《不可思议的e》获2009年度国家科学技术进步二等奖。
这位老人自娱自乐没有错，但一位科普书作者，不假思索地抄录网上的一段报道，将无聊当趣闻，缺乏科学精神。
3 精品难出：评蔡天新的作品
我们的目的不是指责韩雪涛先生。相反，韩雪涛先生写了这么多作品，是难能可贵的。
说难有两个原因：
一是普及图书需要作者具备广博的知识以及审慎的态度。
二是在目前状态下，很多专业数学工作者没有献身精神，不做这件事情（实际上也可能做不好）。
数学工作者的错误蔓延至人才公园这个深圳市用来彰显城市精神的重要公共空间，反映了一个现象：不少数学普及读物的内容真中有假，一般读者难以辨别。特别是有影响力的作者产生的错误，容易使数学水平不成熟的读者接受。
很多例子可以说明难以出完美无瑕的作品。
如商务印书馆出版的大学数学教师翻译的图书，专业杂志《自然辩证法通讯》上专业人员写的文章，我们都见到过因为不懂德语又没能仔细查阅核对而出现德语常见名词的错误翻译。
笔者曾在文章中也犯过很可怕的错误，在《数学文化》第4卷第2期第44页右栏中，称2的立方根为超越数，所以不能用尺规作图解决化圆为方问题。我猜测当时也是没动脑筋，也可能受到一些文字的影响而犯此类错误。（在有限的时间内写作长篇文章是很累的。）
我们的影响力较小，能力有限。
我们不妨以浙江大学著名数学教授兼诗人蔡天新的作品为例来作进一步说明。需要说明的是，我个人是很尊重蔡天新教授的。我是奉命为蔡教授“雅正”，只是为了说明好书，没什么错误的好书是很难得的。
蔡天新的科普代表作有两本。
一是商务印书馆于2016年出版的《数学传奇——那些难以企及的人物》（以下简称《数学传奇》）。该书获得了2017年度国家科学技术进步奖二等奖，其前身是他在2009年出版的随笔集《难以企及的人物：数学天空的群星闪烁》。后者在出版当年就曾获将，部分编目被翻译发表，包括美国数学会的杂志。
二是中信出版集团于2017年出版的《数学简史》，它是蔡天新于2008年、2012年两度出版的《数学与人类文明》的修订版，其中2012年的版本曾入选2014年度国家新闻出版广电总局向全国青少年推荐的百种优秀图书。
但就是这两本有很高声誉，经过了约10年时间打磨的书，仍存在一些硬伤。
3.1 《数学传奇》中的一个错误
《数学传奇》182页倒数第一行到183页第1-2行，作者写到：高斯提出了被后人称为素数定理的猜想，也即不超过x的素数个数为x/log x……。
正确的表达是：当x充分大时，不超过x的素数个数(记为π(x))近似为x/log x,或写为
值得注意的是，这个错误就发生在数论领域——这个蔡教授自己的专业战场。
3.2 《数学简史》中的一个错误
《数学简史》谈的数学多些，更容易犯错。让我们将《数学简史》翻到216页。在这页的第二段，蔡教授写道：
“在那个年代，由于人们对实数系缺乏认识，因而存在一个普遍的错误，就是认为所有连续函数都是可微的。”
这里蔡教授将问题理解错了，当时的数学家没有这么笨，会认为所有的连续函数都是可微的。我们不妨复习下高数第一课：连续函数不一定（处处）可微，如定义在实直线上的函数x-->|x|就是这样的例子，它在原点处有个尖点，是不可导（微）的。
实际上，当时数学家普遍的错误是认为，连续函数只在一个孤立点组成的集合上不可微,例如，容易想到有只在有限个点出不可导的连续函数。所以，当维尔斯特拉斯构造出处处连续但处处不可导的函数时，令数学界大为震惊。此外，蔡教授将当时人们的错误归于“对实数系缺乏认识”也不尽然。
4 如何改进
如蔡天新教授这样成熟的作品仍有错误，可想象一般图书是怎样的境地。
我们也再举前面提到的文章和书中的错误为例吧。
韩雪涛《圆周率π的计算历程》是一篇结构和思路都不错的文章，但其中还有多处错误：将钱宝琮著《中国算学史》出版年份1932年（民国二十一年）写成了1931年；将用无穷乘积表示圆周率的沃利斯公式发现的时间1655年写成了1650年。
《说不尽的圆周率》书中第32页第一行有公式
.
实际上，如我们之前的介绍，这里应该用等号。
怎么办？作者应该珍惜其影响力。认真写好每一句话，每一行字，每一个标点符号。
现在很多药剂上往往会指明药剂的副作用。书籍也是如此，应该有人在肯定其作用的同时，说明其中的问题。
4.1 评论家的勇气和担当
不可否认的是，蔡天新教授的作品确实有独到之处。
所以，蔡天新教授的数学作品获得了许多数学工作者撰文称赞以及诺贝尔奖获得者物理学家杨振宁院士和作家莫言，数学家彭实戈、张益唐院士等的推荐语。
问题在于，鲜有批评声。有一些专家，知道蔡教授书中的不足，但出于中国人的中庸之道，不愿意公开批评蔡教授的作品。
最好的称赞就是批评。如此能使作者的作品得到改进。
4.2 不能仅仅提倡献身精神
数学界为何没能为设计师以及广大读者提供良好的可供参考的科普资源？如很多高校教师对花太多精力，无益于自身职称评定的事情还是不愿意做。可以理解，这是现实。
在目前状态下，不求名利地写好每一句话都需要献身精神。国家、城市和公众如果要得到好的数学知识和数学精神传播品，仅仅提倡献身精神不是长久之计。
4.3 国家的重视
好的科普很重要。杨振宁先生就多次以自身经历说明“好的科普工作是有好的社会作用的。”
现在，科普也得到了国家的重视。
习近平总书记也强调：“科技创新、科学普及是实现创新发展的两翼，要把科学普及放在与科技创新同等重要的位置。没有全民科学素质普遍提高，就难以建立起宏大的高素质创新大军，难以实现科技成果快速转化。”
今年1月19日，国务院发布《国务院关于全面加强基础科学研究的若干意见》，也谈到要推动科学普及，弘扬科学精神和创新文化。
5 期待
人才公园从启动到完工，大约半年时间，体现了深圳速度。但文化依赖于积累，科学普及需要时间。科普，包括数学普及，任重而道远。我们期待，有一天，数学工作者可以为设计师以及广大读者提供更多更好的可完全信赖的科普资源；有一天，类似于人才公园π桥上这样的错误少出或不出。
我们无意批评任何人。数学普及作家是一群非常值得我们尊重、爱护的群体。我们指出部分错误，是为了说明我们任重而道远，需要读者、作者一起努力。
2018年4月13日星期五（修订）
关注微信：哆嗒数学网 每天获得更多数学趣文
新浪微博：http://weibo.com/duodaa
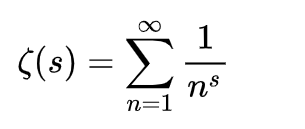
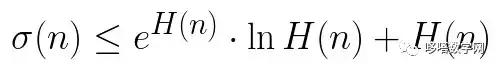
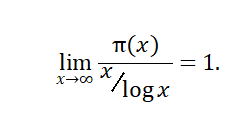
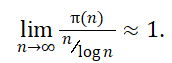
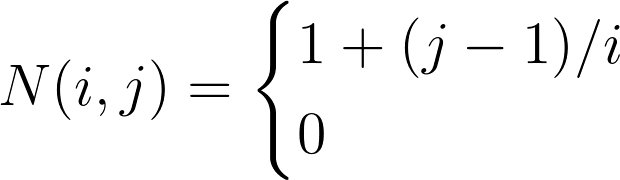
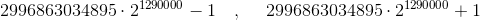
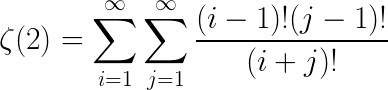
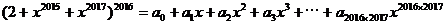，那么 
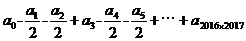的值是多少？
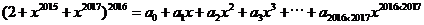，所以常数项容易求，在等式两边令x=0，则有a_0 = 2^2016。但是右边会出现一次项二次项吗？笔者感觉x的最小指数应该是2015，貌似a_1, a_2, ……, a_2014应该为0。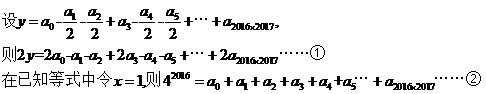
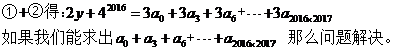
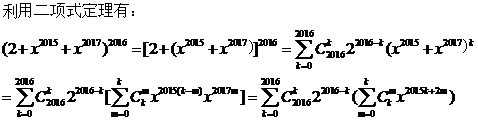
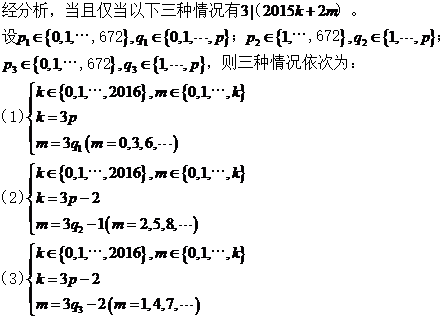
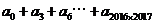，所以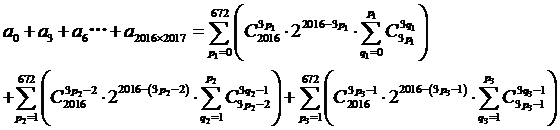
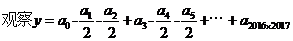，三个一组三个一组，每组中连续出现两个-1/2 ，太奇怪了。由【疑问一】、【疑问二】可知，用常规的实数0,1赋值不可能有这种效果出现。想想我们所见过的成千上万不计其数的数，实数也好虚数也罢，哪一个数的整数次幂会以3为周期，并且同时含有系数 ？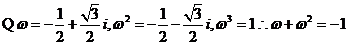
）
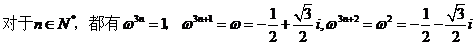
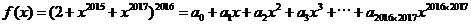
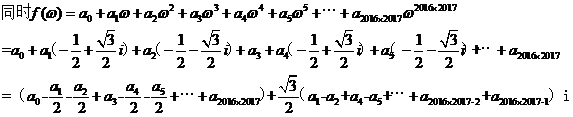
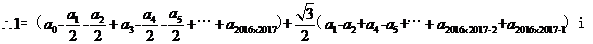
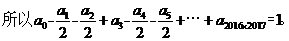
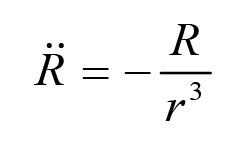
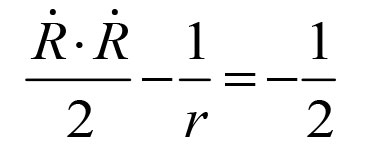
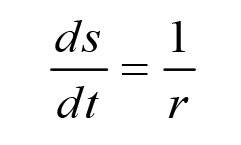
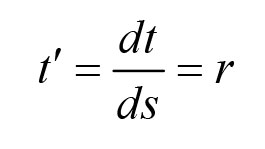
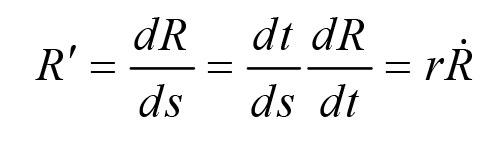
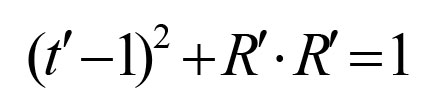
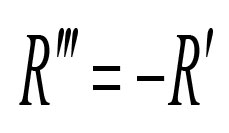
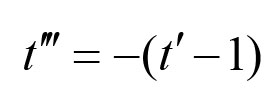
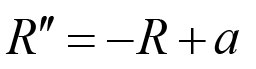
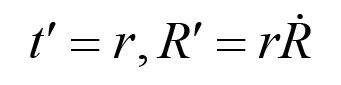
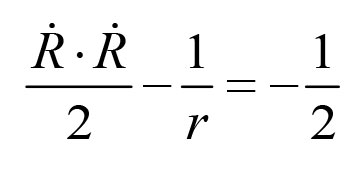
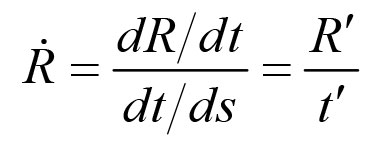
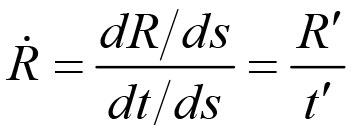