关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

根据中华人民共和国教育部官网消息，教育部学位与研究生教育发展中心公布了全国第四轮学科评估结果。第四轮学科评估于2016年4月启动，在95个一级学科范围内开展（不含军事学门类等16个学科），共有513个单位的7449个学科参评（比第三轮增长76%）；全国高校具有博士学位授予权的学科有94%申请参评。

第四轮学科评估首次采用“分档”方式公布评估结果，不公布得分、不公布名次，不强调单位间精细分数差异和名次前后。采用按百分位进行分档的方式。根据“学科整体水平得分”的位次百分位，将前70%的学科分为9档公布：前2%（或前2名）为A+，2%～5%为A（不含2%，下同），5%～10%为A-，10%～20%为B+，20%～30%为B，30%～40%为B-，40%～50%为C+，50%～60%为C，60%～70%为C-。

数学学科中，全国具有“博士授权”的高校共76所，本次参评69所；部分具有“硕士授权”的高校也参加了评估；参评高校共计182所，进入榜单的共有129所。中国科学院大学的数学学科以科研单位参与了这次学科评估，得到“分档”为A+。所以，本次数学学科共有130个单位进入榜单，北京大学、复旦大学、山东大学、中国科学院大学四个单位获得了最高等级的A+。（注：评估结果相同的高校和单位排序不分先后，按代码排列）

另外我们哆嗒数学网的小编和之前公布的14所数学“双一流”名单做了对比。发现14所数学“双一流”高校中，此次评为A+的3所，评为A的5所，评为A-的3所，评为B+的3所。而评为A-以上(含)的高校或者单位中，有19所高校和单位中，有8所没有进入之前的数学“双一流”名单。这些学校包括浙江大学、武汉大学、南京大学等，通常认为的数学强校。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者，Frank Calegari，芝加哥大学代数数论教授。

翻译作者，Math001，哆嗒数学网翻译组成员。

校对，donkeycn。

五年前，Cathy O’Neil举出了一个有理有据的例子来说明（在五年前那个时间点上）为什么望月新一的声明（仍然）不应该视作ABC猜想的一个正式的证明。关于那篇帖子中讨论的数学的社会效应我这里不再做任何补充了，这里我只想向大家报告一下，在专业的数论学家眼里，现在是个什么情况。具体情况是什么？答案是，这简直是一场彻底的灾难。

这篇文章不讨论关于望月新一证明对与错的认识论上的哲学意义。举个极端的例子，如果望月新一把它的证明用古希腊线形文字刻在石板上，然后丢到马里亚纳海沟里，那么大家可能几乎不会怀疑，追问那证明是否存在过是一件毫不重要的事情。虽然说法极端，而现实情况和刚刚我的这个描述没太大差别。

我从某专家处（不便公开）得知，每一次望月新一的论文分析，结果报告都是让人不安的相似：大量声明的“显然的”结论，而这些结论依赖于巨量的未经验证过的理论。望月新一基于如下观点辩解：格罗滕迪克学派的数学产出也是遵循着相似的模式，而事实证明，这些产出已经成为现代数学的基石。这个典故大概是这样的：

笔者听过这样的故事：有一天，格罗滕迪克说，弄开核桃壳有两个办法。一个办法是，把核桃壳用坚果钳子使劲一口气夹烂。另外一个办法是，把它浸入有很多很多水的水缸里，泡啊，泡啊，使劲的泡啊，然后它自己就泡开了。格罗滕迪克的数学属于后者。

话虽如此，但拿望月新一和格罗滕迪克做对比并不好。是的，格罗滕迪克在20世纪60年代以革命性的方式“完全彻底”的重构了数学。但是，从法国高等研究所（IHES）生产的思想迅速传遍了世界，在巴黎大学、普林斯顿大学、莫斯科大学、哈佛大学、麻省理工学院、波恩大学，以及荷兰的一些大学等等，它们的讨论班已经展开了讨论。本质上，格罗滕迪克学派20世纪60年代的成功并不是用IHES产出的定理来衡量的，而是它产生的思想完全改变了这个学科（以及相关学科）里的每一个人思考代数几何的方式。

这不是对某人个人癖好的吐槽，也不是抱怨某些人不按“体制”的规则出牌。佩雷尔曼也拒绝按照学术圈的通常做法发论文，而是把他的论文简单直接地贴在arXiV上，就撒手离开了（补充：虽然佩雷尔曼从来没有正式提交论文，但他随后开办了巡回讲座，让其他专家接受自己）。但最终的结果是，在数学里，思想是永远的胜利者。人们可以读到佩雷尔曼的论文，能在文章中感知到他所有的思想(五年内，大量专家补充了原始证明里略过的完整细节，并陆续发表)。通常情况是，如果数学领域里有突破性发现，当其他数学家能利用这个新的思想证明其他领域的定理的时候，这个标志性的事件会引起学术成果爆炸式的增长。而且，通常这些事件并不能被理论的原创者预先感觉到。但这样的事情，并没有在ABC猜想的证明上发生。这样的现实下也就难怪人们对该证明如此强烈的质疑了。

事实是，现在这些论文似乎要被PRIMS(这是望月新一自己当主编的杂志，这事本身不是什么大问题，但依然有碍观瞻)接收了。被这样的杂志接收，并不能成为人们接受证明的理由，该证明的现有处境依然没有改变。如果说审稿程序有什么意义的话，那么它的意义就在于使人在一定程度上相信文章的正确性。(虽然有时候发表的文章也会有一些错误，但这些错误一般很快就能被比较专业的读者修正，或者有时候会发一个勘误表，当然也有很稀少的文章被撤回的现象）。也就是说，它迫使作者用清晰的文字，写出标准范式的语言，让专业人士能读懂文章（所以，除了其他特别的原因，审稿人不需要花费像作者需花费的那样多时间来审论文）。而在这件事情上，上面的功能就完全失效了，质疑会同时来自两个方面，审稿人对文章质量的评定，以及PRIMS编辑委员会对论文会以这样不可接受的，被广泛认为不透明方式发表的放任。那么，我们会进入一个荒唐可笑情形——ABC这个命题在京都是定理，但在其他地方都是猜想。（补充：一位日本读者向我指出，报纸并没有确定地说论文已经被接收，用的是“按计划论文会被PRIMS接收”诸如此类的措辞。这也不会改变本文的实质内容，这里还有论文不会以现有方式被接收的可能性，如果那样的话，我收回对PRIMS编辑委员会的批评。）

那么为什么这样的情况持续了那么长的时间？我想我能提出三点基本理由。第一，数学家通常是非常小心翼翼的（说个笑话——苏格兰的绵羊至少有一面看上去是黑色的）。因为数学家们不能指出望月新一证明的实质性错误，所以他们非常不愿意去声明这个证明有问题。于是，他们倾向于对任何一个关于错误的声明用极端谨慎（足够合理的谨慎）的态度。我们成长为数学家的历程中，如果听不懂别人的证明过程，通常会自我觉得很丢脸。第二，无论何时，数学家一旦做出一个特别的声明，大家开始的反应都会去看这位数学家之前的工作。这里，望月新一曾经在重要领域做出过成果，而且被很多认识他的人认为是一位智商很高的数学家。的确，一些默默无闻的人（比如最近的张益唐就是一个例子）声明自己证明了某个重要的结果，他的文章也会被认真对待，但是，如果类似不知名的人以望月新一的方式放出一个1000页的论文，他立马会被拒掉。最后一个理由，对比前两点，一些人愿意看到论文被公开，以及听到一切都很好的消息，而质疑者们也没有为理解望月新一的宇宙际几何的基础而做够功课。我没兴趣去揣测人们为什么这样做。但是，这种至少需要几百小时才能入门的理论要么是彻头彻尾的垃圾，要么是超越现有所有既有知识的体系。那么，不仅在数学上，而且在所有科学里都是前无古人的。

那么，事情会怎么发展？这里有很多种可能。一种可能是某位专家深度检查了论文，并能抽出论文的核心思想，然后对论文主干进行简化修改，让它更容易读懂。这是论文放出后梦想中的剧情发展，但一天一天地（一年一年地），这个可能性变得越来越小。但可能性仍然存在。与之相反的可能是，某位专家找到了一个严重的错误，用否定的方式来了结这个事情。第三种可能是，这个状态一直持续下去：没有“恩赐的一击”（编者注：人奄奄一息时给的最后一下，让其免于痛苦）来杀死证明，但是同时江湖上仍然在流传没人能领会论文中心思想的传说。（我想说论文是否被某个杂志接收和此毫无关系；这不是证明人们读过论文并认为论文没有问题的适当方式，必须有人能解释论文。）这种情况下，数学界会一直这样摇摆反复下去，可能会持续一年、十年或者一百年。直到有人最终证明了ABC猜想，然后回过头来对比，来看看那种证明的思想究竟是否真的一直在那里（大结局）。

陶哲轩在本文评论区的回复：

感谢博主的文章。我没有足够的专业知识去对望月新一的论文做一个直接的评价，但是对于你文章中提到张益唐及佩雷尔曼的工作却更加熟悉。它们之间一个显著的区别在于张益唐与佩雷尔曼的工作里有着较短的“方法验证”，即用他们的方法能很快得到相应领域里一些很有意思的不平凡的结论（或是发展出一些已有不平凡结论的新证明）。这些事情发生在论文发表之后，而不是之前。

在佩雷尔曼的工作中，第五页就已经给出了Ricci流的一个全新解释：它将Ricci流看成了梯度流，而这是一个看起来非常有前途的方法。在第七页，他就用该解释建立了一个关于Ricci流的非常精彩的定理。虽然这个定理离最后证明庞加莱猜想还有千里之遥，但是它本身就是一个新奇且有趣的结果。这也是为什么这个领域的专家迅速认定这篇文章中有很多“好东西”。

在张益唐54页的论文中，有很多对专家来说是标准性的内容（特别地，这篇文章沿袭了解析数论界的传统，将所有要用到的引理放在了文章的开头）。但是仅仅6页的引理陈列之后，张益唐就从中做出了不平凡的观测：只要能改进Bombieri-Vinogradov定理对光滑模的估计，我们就能证明素数间距离有限。（其实这个观测也被Motohashi和Pintz独立地导出，但其形式却无法被得心应手地运用在张益唐后面30多页的证明中）。这并不是张益唐论文中最深奥的部分，但是它却将原问题化为了一个看起来更容易处理的问题。与无数试图攻克像黎曼猜想等大问题的论文相比，它没有将原问题不断转化为看起来更复杂的问题（只有奇迹发生，才能将这些复杂的问题转化回一个简单的问题。）

从我了解的信息来看，对于望月新一所用的方法，最短的“方法验证”就是300多页ABC猜想的证明。如果能有一个更短的 “方法验证”（比如少于100页）就可以帮助人们消除对于这篇论文的怀疑。 如果说一个300多页的独立体系只能用来证明ABC猜想，且这个体系里不能衍生出任何证明其它结论的子方法，这将是一件非常邪门的事情。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

我必须坦诚交代我曾经对长数轴（long line）有着微微的敌意。但是当我看到Mike Lawler发的推文的时候，我觉得应该给再长数轴一个表达自己的机会。

Mike Lawler: 
我对你的爱就像长数轴 —— 真情如往，仅更久长

就是说，长数轴是拓扑空间中的一张甜腻腻的情人节卡片。是否能找到它背后所有的意义，就是让我在数学里找寻爱情的表达，最幸福的事情莫过于此。

就像它名字表达的那样，长数轴真的很长，某种意义上说它比通常的实数轴“长”。我们能把通常的实数轴看成一串单位长度的区间一个接着一个拼接而成的直线。或者说明确一点，区间的个数与整数一样多。长数轴基本也一样，只不过区间的个数与实数一样多而已。

无论如何，如果这样的长数轴能作出来，应该是很赞的事情。但是，真相有点诡异，它会让我们撞入集合论错综复杂的旅程之中。集合论中关于无穷的很多断言曾经让数学家康托疯掉。我这里有言在先！

为了定义长数轴，我们得先讨论一下不同数量的无穷。当数学家们讨论集合的数量，或者说集合的基数，他们用的思想是一一对应：如果两个集合中，从第一集合里取出的每一个元素，都能从第二个集合取出一个元素与之配对，一个不多也一个不少，我们就说这两个集合有相同数量。换种说法，如果我们不想数手指的话，我们把两个拇指对起来，再把食指对起来，一直下去，直到把两只手的所有手指都对应了起来，于是我们知道，两只手的手指数量是相同的。

当我们把此方法用于无限集合的时候，奇怪的事情就会发生。虽然偶数只是整数的一部分，但是整数和偶数是一样多的。我们可以把整数写在左边一列，偶数写在右边一列，左边写n的地方，对应的右边写上2n。于是，我们找到了一个一一对应，这两个集合元素的数量是一样多的。然而对于有限集，你是找不到这样的一个一一对应的。

.
实数集合已经被证明是比整数多的，所以我们知道了至少有两种不同数量的无限集合。实际上，我们有从一个数量少一些元素的集合得到元素数量更多的集合的一般方法。所以，我们可以从整数的无穷开始不断生成无穷多个拥有元素数量越来越多的无穷集合。对于整数集合的无穷，我们把它叫做可数无穷。

这和我们要说的长数轴有什么关系？长数轴的确切定义其实不是用实数多个单位区间拼起来。而是把最小的不可数无穷(smallest uncountable infinite)多个区间拼在一起而组成的。

到了这里，我们将撞入连续统假设问题。连续统假设是说实数的无穷就等于最小的不可数的无穷。所以，如果实数的基数和最小的不可数的无穷相等，那么我先前长数轴的描述才是准确的。如果不是，实数无穷和整数无穷之间还有别的无穷的话，构造长数轴的区间数量应该用那个最小的不可数无穷替代。

那么，连续统假设是真的吗？好消息是，你认为它是真的是没问题的！1963年，Cohen证明了连续统假设和决定数学底层的策梅洛-弗兰克尔公理系统不矛盾。连续统假设不成立，也和策梅洛-弗兰克尔公理系统不矛盾（编者修正：这是一个误解，实际上连续统假设与策梅洛-弗兰克尔公理系统不矛盾在20世纪30年代就由哥德尔证明了，Cohen证明的只是后者，即，即便连续统假设不成立，也和策梅洛-弗兰克尔公理系统不矛盾）。就是说，连续统假设这个命题和数学的公理体系是独立的。你不可能用现有的数学公理证明或者否定连续统假设。一些人认为，这说明我们的数学底层还不完美，但我更倾向于支持另外一种说法——我们可以在一些没有矛盾公理体系之间自由切换。

我们是否决定接受连续统假设，取决于我们用长数轴能做多少事情。它有什么好处？和许多我喜爱的拓扑空间一样，长数轴可以用来打破你之前喜爱的数学用具——这是一个绝妙的反例。在这种情况下，长数轴告诉我们如果我们有太多好东西，也许并不一定是好事。最基本的，在长数轴上，我们不能建立微积分体系，因为它太长了。

至于原因，这牵涉到很艰深的技术手段，特别是你刚刚费尽脑汁思考完“最小的不可数无穷”的时候，我们来说说建立微积分体系要满足的三个条件也许更容易接受一些：第一，从局部看，它要和某个维数的欧氏空间相似；第二，它得是豪斯多夫的，就是说你可以让空间内的点分离开；第三，它还得是第二可数的，就是说它能从比较少（可数多）的集合中构建出来。长数轴不满足最后一条。虽然，你可能认为长数轴基本上和普通实数轴一样，但是它们其实有根本的不同，就是因为长数轴太长了。

“吾爱汝深深几许？今且听吾细数之…”(How do I love thee? Let me count the ways…)，如果你心里总惦记长数轴的话，这勃朗宁夫人的诗句听起来也没那么动人了，“吾爱汝深深几许？勿可令吾细数之,犹如集构长数轴, 实为永世不可数！” 虽然诗意少了些，但貌似能更浪漫的表达你的感情！

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

这可能是10年来数学界最大的新闻：根据朝日新闻的报道，望月新一关于ABC猜想的证明，有可能发表，并予以确认。现在论文还在做最后的同行评议，如果没有问题，发表时间可能是明年1月份。

ABC猜想是数论领域最重要的猜想之一，于1985年提出。2012年8月，日本京都大学教授望月新一在其个人网站上贴出了该猜想的证明。该证明初版500多页，几经修正后达到600多页。由于望月新一的采用方法极其独到、创新性极强，文章又非常长，一时间数学界竟无人能理解其证明。当时有数学家认为，要理解望月新一的证明，可能需要数十年时间。

数论中，有很多著名问题都是ABC猜想的推论。比如我们列举的下面三个，曾经是数学界的神级问题，但在ABC猜想面前，就是简单的特例了：

莫德尔猜想： 该猜想于1984年被法尔廷斯证明。法尔廷斯因此获得1986年的菲尔兹奖。该奖被誉为“数学界的诺贝尔奖”，是数学研究的最高荣誉。

费马大定理：该猜想于1995年被英国数学界怀尔斯证明，轰动全球。初版证明300多页，精简后也有100多页。如果利用ABC猜想，将极大简化费马大定理证明。

比尔猜想：该猜想由比尔本人提出，并通过美国数学会悬赏100万美元求解。难度极高，用比尔猜想，你可以不超过5句话证明费马大定理。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

你即将搬家，所以你得在子事先没有过目的情况下租一个新的公寓。你网上也找了，电话也打了，终于相中了一个看上去不错的房子。但你到了你的新家的时候，总觉得有的地方…昏暗无比。实际上，房间所有地方都黑漆漆的，因为根本没电。你重新去翻看房屋出租的广告，的确，广告没有任何地方强调了房间就通电的，但你不会考虑你需要将这件事情当成一个问题去询问房东。

对于很多数学家来讲，豪斯多夫性质就像一个房间就应该通电一样自然。当然，你能构造一个不是豪斯多夫的空间，但你研究问题的时候，多少会认为，一个正在思考的空间是豪斯多夫的。在一个不是豪斯多夫的空间里做拓扑问题，那种感觉和在一个乌漆嘛黑的房间里乱撞没有区别。豪斯多夫性质是以德国数学家费利克斯·豪斯多夫的名字命名的。豪斯多夫性质描述的是数学空间中关于分离性的众多性质中的一个：空间中的点，它们之间的的分离程度到底有多大？一个拓扑空间是豪斯多夫的意思是，任意两个空间中不同的点，都能把它们分别放入两个不相交的开集里面。开集是拓扑空间中最基本最普遍的概念，你可以看看我们之前的文章，来了解一下为什么开集如此重要。

为了进一步了解豪斯多夫性质的重要性，我们来思考一些常见的空间，比如说实数轴。实数轴中的开集就是那些开区间(编者注：以及开区间并起来得到的并集)，比如(0,1)。两个数轴上的点，无论他们距离有多近，他们之间总有一个距离区隔，所以我们能找到两个足够小的开区间，这两个开区间各自包含了一个点，并且这两个区间没有重叠的部分。
 

其他常见的空间——诸如二维欧氏平面、三维欧氏空间——同样具有这个性质。我们似乎有点难以想象一个空间没有这样的性质。这里我们来引出一个有两个原点的数轴——最简单的没有豪斯多夫性质的空间之一。

为了作出一个有两个原点的数轴，我们从作普通的两个数轴开始做工作。我们标记好两个普通数轴上的点，上面那条数轴的点为(x,0)，下面那条上的点为(x,1)。现在，我们说我们把除了x=0以外的所有的(x,0),(x,1)这样的点都看成相同的点。而且我们设定，新的空间继承之前那两条普通数轴的通常拓扑，就是说，新空间的开集还是由那些开区间组成。

你可能无法接受我们把那样的两个点看成相同点的设置，但是思考拓扑问题的时候我们必须设定一些类似这样的规则。就像乔治·奥威尔的小说《一九八四》中设定“我们和东亚国的战争永无完结”（We have always been at war with Eastasia）一样，(1,0)和(1,1)在我们的设定中就是相同的点。

你能明白有两个原点的数轴不是豪斯多夫的原因吗？毫无疑问，定义中“除了x=0”引起了我们的注意。在上面的那条数轴中，每个包含(0,1)点的开区间，都和下面数轴中包含(0,1)的开区间有重叠的部分，这是因为两条普通数轴中，几乎所有的点都是相同的点。

虽然，我在本文中画了一些图形，但是仍然难以用准确的图形展示有两个原点的数轴。实际上，我们能在数学上证明我们不可能画出有两个原点的数轴，这也是豪斯多夫性质之所以重要的原因之一。一个没有豪斯多夫性质的空间是很难直观的展示的。但是一个空间如果满足豪斯多夫性质，那么我们就可以以某种适宜的方式将它纳入到某个欧氏空间，或者维数再高一些的空间中讨论。两个原点的数轴不能嵌入到任何一个欧氏空间来展示它的本质。于是，我们退而求其次，我们在纸上或者电脑屏幕上作图的时候，会省略掉一些点和线，希望读者能大致能理解。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

这是一套有日本数学会强力推荐数学科普书。原版在日本销售破40万。这回在人民邮电出版社放出《数学女孩3：哥德尔不安完备定理》中文版之际，我们再次推荐这套书的《数学女孩1》、《数学女孩2：费马大定理》、《数学女孩3：哥德尔不安完备定理》三本中文版合集套装。

《数学女孩1》： 讲述了很多数列和级数的知识！

《数学女孩2：费马大定理》：讲述了很多初等数论以及群环域等抽象代数的知识

《数学女孩3：哥德尔不完备定理》：讲述了很多数理逻辑、集合论、经典分析学的知识。

这是一个用数学串联所有线索的青春故事书。男主角人见人爱，虽然不是最强，但也聪明上进。三位女主角性格各异，在男主角的带领下，攻克一个又一个的数学问题。我们来看看书中的人物，如果你经常看日系漫画能领略其中风格。注意，我们这回推荐的是全文字的原版，而这里配图用的是它的漫画版本，注意区别。（漫画版本省略了很多数学部分，暂不推荐） 

主要人物

“我”： 

本作品的男主角，《数学女孩1》里面是高中一年级，后慢慢升入高二、高三，在家中是位独生子。非常喜欢数学，不满足与课本和课堂上学到的东西，经常找很多高深的数学课外读物和问题研究。在学校偶然认识了数学水平非常高的米尔嘉同学，开始男孩女孩之间关于数学的切磋历程。另外，经常在指导数学=学学习有困难的学妹泰朵拉，后来就当起了泰朵拉的私人家教，在图书馆、咖啡厅等地方非常耐心的解决数学问题。有时候会不经意的注意到身边女性的情感。也经常在家里教表妹尤里数学。

米尔嘉

女主角之一，男主角的同班同学，十分会弹钢琴。和其他人一样都是数学的爱好者。数学水平在男主角之上，男主角也经常找米尔嘉请教或者讨论数学。高中阶段已经能熟练的使用一些诸如群论、数论高等数学解决问题，方法简练却又不失严谨。人的外在表现比较高冷，但也时常表现出柔弱的一面。米尔嘉经常和男主角、泰朵拉、尤里一起讨论数学问题，高中毕业前收到美国大学的邀请出国留学。

泰朵拉

比男主角小一届的学妹，在初中时和男主角同校并且对他有好感，后来又念了同一所高中。数学较弱，遇到排山倒海般的算式或是学校老师解释不清楚的观念时会受不了。受到了男主角的指导而学会一有问题时就要积极发问，确认自己懂了，整理好思绪后才会继续前进。个性有点天然呆。在男主角指导下，数学进入了全年级前10%。

尤里

男主角的表妹，在家中是独生女，小男主角三岁，会称呼男主角为“哥哥”。由于自家和男主角的家相当的近，便经常到他家中作客，喜欢在男主角的房间看书，常出题给男主角。把自己自认为“猫女”，会在撒娇时发出“喵”的声音当作语末助词。

其他人物

盈盈

非常擅长钢琴，经常和米尔嘉一起练习钢琴。在书中戏份不多，没怎么进入主角们的数学世界。

村木老师

一位古怪的数学老师，喜欢男主角和米尔嘉。常出一些和课程内容无关，但是很有趣、且值得探讨的题目，也就是“研究课题”，并习惯写在卡片上给主角们带回去思考。不会硬性要求要回答，但是主角们还是习惯会提交报告给老师。

都宫

擅长运动，数学成绩全年级第一，但是并没有实际参与主角们的讨论、活动。前期，偶尔出现。

瑞谷老师

图书室的女性管理员，时间一到就会宣布闭校、放学时间到了。

“我”的妈妈

很喜欢尤里来家里作客，每次到来，都会用上好的料理招待。和所有的日系妈妈一样，每当气氛尴尬的时候，她就会出来说：“喝杯茶吃点东西再聊吧！”

当然，最后的结局往往都是——大圆满！下面是《数学女孩3》的结局。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

原文作者，Evelyn Lamb，数学及科学普及自由作家。

翻译作者，Jessie仪，哆嗒数学网翻译组成员。

校对，donkeycn。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

数学总是将可定向亏格比作一种甜点，即拓扑例子里最美味的那种。

 
.
啊，这个简单的环面是拓扑学家们最初的朋友，它也展示了理论与实践的差距。环面有很多特性而且在数学的各个领域都会出现。第一，他有一种拓扑的特性。拓扑学并不关心你看它的具体形状像什么，它只关心大体上的特征。具体来讲，它关心物体在没被撕裂或粘合的情况下，那不论是被拉伸还是被压缩都不改变的方面。在拓扑世界中，环面是一种带着一个洞的二维空间，或者说是一个曲面。（更高大上说来，它是一个亏格为一的可定向曲面。）急于将他们自己与更吸引人的烘焙学科联系在一起的拓扑学家们将环面描述为甜甜圈，虽然在某种无聊的精确角度来看，它其实仅仅是甜甜圈表层的糖浆涂层。（甜甜圈的面包胚是一种叫做实心环面的三维空间。）
.  

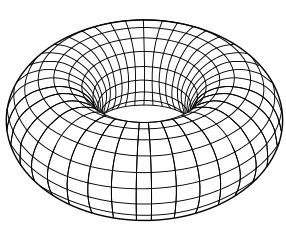
我们经常以一个被完美充起的甜甜圈来代表环面，但是拓扑学家们偏向于以一种更抽象的方式来描绘它。在下面这张图片中，我们将它画成带着几个标记的长方形，这些标记叫做特征点。

  
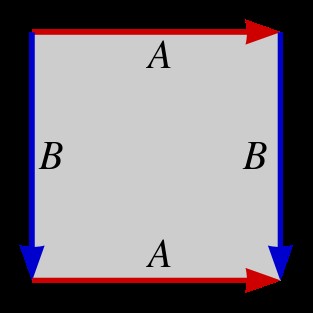
图中上面带“A”的箭头所对应的边和下面带“A”的箭头所对应的边将会被粘合在一起，左面带“B”的箭头所对应的边和右面带“B”的箭头所对应的边将会被粘合在一起。

正如在经典游戏小行星（Asteroids）中，当你从长方形上方的边走出长方形时，你会在下方的边上再次出现；当你穿过长方形的右边时，你会在左边重新现身。这幅图尽管不如甜甜圈那么令人垂涎，但仍然向我们展示了环面所有的重要拓扑性质。

这幅平面的长方形图片也良好承担了通向另一个环面生命的责任：作为几何物体的生命。不同于拓扑学，几何学确实关注实际的形状与距离。一个“环肥”的环面和一个“燕瘦”的环面尽管在拓扑概念上相同，但就几何概念而言，是不一样的。

几何学家们之所以关注这张环面的长方形表示，是因为本质上这是一个平坦的有限平面，就像一个无限平面。如果你曾不愉快地意识到格陵兰岛其实只有非洲大陆面积的7%，而不是和非洲面积一样大，你潜意识里就已经明白了一个事实：球面不可能被保持距离的展到平面上。这是因为球面曲率为正的，而平面是平的（注：曲率为0）。同样存在一种负曲率的曲面，他们也不可能被毫不扭曲地扯平。这个长方形图片展示了“环面是平的”这个事实。那么，这可就太好了，因为这样的话，它就能成为一个三维空间中实实在在存在平坦曲面，从而我们能直接观察到它；而不只是把它画在纸上然后还需要运用我们的想象力去想象。我们可以试着通过操作那些长方形上的被标记的那些边来这么做。我们从一个长方形开始。

 
第一次粘合把一张平坦的白纸变成了一个圆柱体。

第二次粘合将圆柱两端连在了一起。
 

实际上操作起来还是有些困难的。得到这个环面并不像计划那么顺利。这是一个理论与现实的不和谐碰撞。

当它们进入现实世界，当一个数学对象进入现实世界后，一般来讲，它很难再保持完美。我们没法画出一个严格意义圆，而且那个我们用来画图的曲面，也并非一个严格意义下的二维对象。但专心致志与优质圆规可以让我们画出与我们目标足够接近的圆。然而，环面，那可就是个噩梦了。

所以，我们到底能不能把环面放进三维空间中而不改变任何距离？
  

我们当然能！但是这没有你所希望的那么容易。

一个选项是，我们放弃那个完美平滑的曲面。在平面上，那个长方形没有任何折痕，但如果我们搞出一些来，我们就有处下手了。这么干的方法有很多。几年前我就做了一个。
 

数学3D打印的大魔法师Henry Segerman有一个脊被接合在一起的优秀例子。

要是我还不满足呢？要是我想把这些不和谐不雅观的折痕除掉呢？嗯，我们也能这么干！不过这就有点复杂了。在2012年，Vincent Borelli, Saïd Jabrane, Francis Lazarus, Boris Thibert, 以及Damien Rohmer发表了第一批没有任何尖角的三维空间平坦环面的图片。他们写道：“这些图片展露了一个令人意想不到的对象，处于分形和普通曲面的中间：一个平滑的分形。”换句话说，他们将分形的无限特质与一个平滑过程结合到了一起，从而避免了尖角的出现。
 

最后，这个“平坦的”环面看起来一点也不平坦，但它成功体现了它的字面意思。所有的距离都与他们还在那个平面上的长方形时完全一样。（若想进一步了解这种平滑分形的环面，请参见https://www.youtube.com/watch?v=5qu3WETuf6c）

环面还有很多其他变体：在拓扑学中，它是乘积空间中的最初例子之一，也是在运用 Seifert-van Kampen定理的第一次有用尝试。在动力学中，它是学生们最初碰到并能在其上“打台球”的平移曲面之一。在我所研究的领域，Teichmüller 理论，这是少有的几个简单到你真正可以理解并进行计算其Teichmuller空间的空间之一。一般来说，环面看上去就是那种每当遇到了新观点时，值得用千百种定理来描述的例子。带着感恩节季的精神，就让我们花点时间来感谢环面，因为它是让我们无论在二维几何还是拓扑学中都可以染指的好例子。（毕竟，数学总是比一个可定向亏格为一的甜点要好。）

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

2018“科学突破奖”颁奖典礼2017年12月3日在位于旧金山的美国国家航空航天局（NASA）阿姆斯研究中心揭晓，旨在表彰生命科学、基础物理及数学领域最杰出的成就的研究人员单项奖金为300万美元，此次共颁发2200万美元奖金，从奖金来看的确为科学界第一巨奖。

本次数学奖由来自美国犹他大学的克里斯多夫·哈康（Christopher Hacon）和来自美国加州大学圣地亚哥分校的詹姆斯·麦克南（James McKernan），一起获奖，分享300万美元奖金。另外，还有4位数学家获得3个数学新视野奖。中国数学家，恽之玮和张伟分享了其中一个奖项，该项奖金10万美元。值得一提的是，两位中国数学家都毕业于北京大学——北大的数学简直太厉害了。

“科学突破奖”有着“科技界的奥斯卡奖”之称。之所以有这个称谓除了高额的足以吸引任何媒体眼球的奖金意外，还有一个原因便是它的颁奖典礼星光璀璨，聚集了科学、技术、娱乐等各界明星——之所以这样颁奖，我们能从该奖项赞助人之一的尤里·米纳尔的话中，探知一二：“我小时候，占领各个版面头条的都是科学家，而现在情况全变了。我认为，这些改变世界的科学家们，完全有理由被世人知晓”。

以前，我们只是报道一下获奖情况，很少有人介绍颁奖典礼的具体过程。这回，我们随小编一道，以2018颁奖盛典为模板，让大家来看看，这个“科技界的奥斯卡奖”的颁奖盛典。

当然，我们哆嗒数学网作为一个身在中国的数学普及公众号，会更多的聚焦盛典的中国元素和数学内容。

先说说这个奖项的资助人。资助人可都是互联网和科技界的大咖，除了刚刚说的尤里·米纳尔，还有谷歌的联合创始人谢尔盖·布林、脸书创始人的扎克伯格、23andMe联合创始人安妮·沃西基。当然，还有中国人都知道的阿里巴巴的马云。以及刚刚不久前加入成为赞助人的，另外一个大家耳熟能详的中国互联网巨神腾讯公司创始人马化腾。

既然是奥斯卡奖，当然不会缺少走红毯的环节啦。让所有杰出的科学家享受巨星般的待遇是这个盛典的目的之一。下面就是恽之玮和张伟出现在红毯上的照片。

典礼开始前，会有一个比较热血的开场白，这几年这个念白似乎一直没变过：

“今晚在美国硅谷一号机库和航空航天局阿姆斯研究中心现场。科学界、技术界和好莱坞最璀璨的明星们齐聚一堂。他们将把超过2500万美元的奖金颁发给在生命科学、数学以及物理学领域的有杰出成就的人士。——这就是“科学突破奖”，他们是改变世界的科学家！”

念白完毕，LOGO登场。

当然，每一次颁奖典礼都会有一个主持人，这一次的主持人是，很多人眼中的“上帝”——摩根·弗里曼。

在台下，我们也发现了曾在中国红极一时的超级“网红”——“奶茶妹妹”章泽天。现在她是京东创始人刘强东的夫人。

当然，任何庆典都不会缺少音乐。这回的音乐表演是由超级巨星大提琴手兼演员欧阳娜娜（大会背景旁白就是这样介绍的）和多次获得格莱美奖提名的嘻哈说唱超级巨星歌手维兹·卡利法共同演出。大提琴和说唱的结合也蛮有特色的。

伴奏中，还有中国鼓。

表演结束后，主持人弗里曼再次感谢了欧阳娜娜，并向来宾们强调，2000年出生的欧阳娜娜只有17岁。这引来全场的欢迎，欧阳娜娜也起身向周围表达谢意。

庆典上，主持人弗里曼从生命科学家和其他人们一直在和各种疾病做斗争，引出了两段悲伤的故事。其中一段是关于数学家米尔扎哈尼的。这位当今唯一一位获得过菲尔兹奖的女性今年因为乳腺癌去世，享年40岁。而庆典中展示的米尔扎哈尼2014年从时任韩国总统，同样是女性的朴槿惠手中接过菲尔兹奖的照片，让人唏嘘不已，感慨世事无常。

2018“科学突破奖”的数学奖的颁奖嘉宾有两位。一位是曾经红遍全美的NFL橄榄球球员、麻省理工数学博士约翰·尤索，另外一位是DeepMind创始人戴密斯·哈萨比斯。DeepMind公司制作出的围棋人工智能软件AlphaGo，打败了人类最强棋手的。

颁奖之前当然是获奖者的VCR，视频大概1分50秒，视频中哈康称自己是一个“Slave Driver”，好吧，这是一个俚语，我们强行翻译成了“大恶人”。

两位获奖人领奖。获奖感言是由哈康一个人说的。他表达了希望更多的研究人员进入他们所在领域的意思。他还强调他们会乐于和所有进入该领域的人分享最深刻的研究成果。

最后全体获奖人员上台，大结局。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa