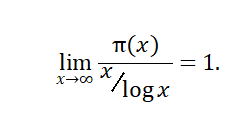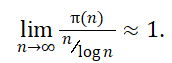原文作者，圣安德鲁斯大学数学与统计学院。

翻译作者，mathyrl，哆嗒数学网翻译组成员。

校对，math001。

  

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

从今天起，我们将连载这部数学编年史。本文是翻译版本，因为工作量巨大，必有疏漏（包括原文也会有错误），欢迎指正。

 

这应该是网上最全的数学编年史，从公元前30000年到公元2000年，哆嗒数学网为你奉献。

 

 这里是 数学上下三万年（六）：十九世纪下半叶的数学

 

这个时期发生了一些著名的战争或者变革，比如普法战争、美国南北战争、日本明治维新。中国的“师夷制夷” 、“中体西用”的洋务运动也在这个时期内开展。各种科学学科已经很接近于现代，从书写习惯来讲，大部分现代课堂上学到的数学，基本始于这个时代。

  

本期出场人物有：切比雪夫、波尔查诺、刘维尔、黎曼、哈密顿、布尔、魏尔斯特拉斯、莫比乌斯、戴德金、西罗、吉布斯、埃尔米特、康托、庞加莱、博雷尔、希尔伯特、阿达玛等。

 

 

本系列下面是往期内容：

 

数学上下三万年（一）：爱在西元前

 

数学上下三万年（二）：从罗马时代到中世纪

 

数学上下三万年（三）：大航海时代

 

数学上下三万年（四）：欧洲资产阶级革命开启

 

数学上下三万年（五）：十九世纪上半叶的数学

 

1850年

切比雪夫（Chebyshev）出版了《论素数》（On Primary Numbers），其中他证明了素数理论的新结果。他证明了伯特兰猜想：对于n>1，在n和2n之间至少存在一个素数。

 

1850年

西尔维斯特（Sylvester）在他的论文《关于一类新的定理》（On a New Class of Theorems）中首次使用了“矩阵”一词。

 

1851年

波尔查诺的书《无穷的悖论》（Paradoxien des Undendlichen）在他去世三年后出版。该书引入了他的关于无穷集合的想法。

 

 

1851年

刘维尔出版了关于特定超越数的存在性的第二本书，这种超越数被称为“刘维尔数”。特别地他给出了一个例子：0.1100010000000000000000010000...，其中在第n! 位为1，其他位为0.

 

1851年

黎曼（Riemann）的博士论文包含了极其重要的思想，例如“黎曼曲面”及其性质。

 

 

1852年

西尔维斯特建立了代数不变量理论。

 

1852年

古德里（Francis Guthrie）向德摩根提出了四色猜想。

 

1852年

沙勒（Chasles）出版了《高等几何》（Traité de géométrie），其中讨论了交比、线束（pencils）、对合，这些概念都是他引入的。

 

1853年

哈密顿出版《四元数讲义》（Lectures on Quaternions）。

 

1853年

谢克斯（Shanks）计算π到小数点后707位（在1944年人们发现谢克斯从第528位开始算错了）。

 

1854年

黎曼完成了特许任教资格（Habilitation）。在他的专题论文中他研究了函数用三角级数的可表性。他给出函数可积的条件，被称为“黎曼可积性”。在1854年6月10日发表的演讲《论作为几何基础的假设》（Über die Hypothesen welche der Geometrie zu Grunde liegen）中，他定义了一种n维空间，今天被称为“黎曼空间”。

 

1854年

布尔初版了《思维规律的研究》（An Investigation of The Laws of Thought on Which are founded the Mathematical Theories of Logic and Probabilities）。他将逻辑归约为代数，被称为布尔代数。

 

1854年

凯莱第一次尝试定义一个抽象群，虽然没有完全取得成功，但是取得了重要进展。

 

1855年

麦克斯韦发表了《论法拉第力线》（On Faraday's lines of force），证明只需用几个相对简单的数学方程就可以表示电磁场的行为以及其相互关系。

 

1856年，魏尔斯特拉斯（Weierstrass）在克雷勒期刊的《阿贝尔函数理论》（Theorie der Abelschen Functionen）中发表了超椭圆积分的反演理论。

 

1857年，黎曼出版了《阿贝尔函数理论》（Theory of abelian functions）。它进一步发展了黎曼面的思想及其拓扑性质，将多值函数作为一个特殊“黎曼曲面”上的单值函数来研究，并解决了一般的反演问题，这些问题的特殊情形已被阿贝尔和雅可比解决。

 

1858年

凯莱给出了由西尔维斯特在1850年引入的术语“矩阵”的抽象定义，并在《矩阵理论笔记》（A Memoir on the Theory of Matrices）研究了矩阵的性质。

 

1858年

莫比乌斯描述了一条只有一个面和一条边的纸带。现在被称为“莫比乌斯带”，它有一个令人惊奇的性质：从中间剪开依然保持完整的一块。利斯廷（Listing）在同一年做出了同样的发现。

 

1858年

戴德金（Dedekind）发现了一种严格的方法用“戴德金分割”来定义无理数。这个想法是他在思考如何教微积分的时候想到的。

 

1859年

曼海姆（Mannheim）发明了第一个带有“游标”的现代计算尺。

 

1859年

黎曼给出了一个有关素数的ζ函数的猜想。尽管在数以百万计的情形下它已被验证是正确的，然而在一般情形下黎曼猜想的正确性仍然未知。它或许是21世纪数学界最著名的未解决问题。

 

1860年

德劳内（Delaunay）出版了《月球运动理论》（La Théorie du mouvement de la lune）的第一卷，这是他20年的工作成果。他通过给出经度、纬度和月球视差的无穷级数来解决三体问题。

 

1861年

魏尔斯特拉斯发现了一条处处不可微的连续曲线。

 

1862年

麦克斯韦提出光是电磁现象。

 

1862年

杰文斯（Jevons）向英国科学协会讲了《政治经济的一般数学理论》（General Mathematical Theory of Political Economy）。

 

1862年

利斯廷（Listing）出版了《对欧拉多面体定理推广后的空间几何体研究》（Der Census raumlicher Complexe oder Verallgemeinerung des Euler'schen Satzes von den Polyedern），其中讨论了“欧拉公式”的扩展。

 

1863年

魏尔斯特拉斯在他的讲座中给出了一个证明：复数是实数的唯一交换代数扩张。

 

1864年

伯特兰（Bertrand）出版了《论微积分》（Treatise on Differential and Integral Calculus）。

 

1864年

伦敦数学协会成立。

 

1864年

本杰明·皮尔斯（Benjamin Peirce）向美国科学会展示了他关于线性结合代数的工作。它利用现代熟知的幂等元和幂零元工具对小于7维的所有复结合代数进行了分类。

 

1865年

普吕克在几何上做出重要进展，他定义了一种4维空间，其中的基本元素是直线而不是点。

 

1866年，哈密顿的《四元数原理》（Elements of Quaternions）在他去世后尚未完成，花了7年时间写成的800页手稿在他去世后由他儿子出版。

 

1867年

莫斯科数学协会成立。

 

1868年

贝尔特拉米（Beltrami）出版了《非欧几何的一种解释》（Essay on an Interpretation of  Non-Euclidean Geometry），其中对罗巴切夫斯基和鲍耶的非欧几何给出了一个具体模型。

 

1869年

吕罗特（Lueroth）发现了“吕罗特四次曲线”。

 

1870年

本杰明·皮尔斯（Benjamin Peirce）自费出版了《线性结合代数》（Linear Associative Algebras）。

 

1871年

贝蒂（Betti）发表了一份拓扑学笔记，其中包含了“贝蒂数”。

 

1872年

戴德金发表了他对实数的形式构造，并给出整数的一种严格定义。

 

1872年

海涅（Heine）发表了一篇论文，其中包含了被称为“海涅-博雷尔定理”的定理。

 

1872年

法国数学协会成立。

 

1872年

梅雷（Méray）出版了《新无穷小分析》（Nouveau précis d'analyse infinitésimale），致力于通过幂级数展示单复变函数的理论。

 

1872年

西罗（Sylow）出版了《关于置换群的定理》（Théorèmes sur les groupes de substitutions），其中包含了著名的三个关于有限群的“西罗定理”。他对于置换群证明了这些定理。

 

1872年

克莱因（Klein）在爱尔兰根发表了就职演讲。他将几何定义为研究一个空间在一个变换群作用下的不变性质。这被称为“爱尔兰根纲领”，深刻地影响了数学发展。

 

1873年

麦克斯韦出版了《电磁通论》（Electricity and Magnetism）。该书包含了四个偏微分方程，被称为“麦克斯韦方程”。

 

1873年

埃尔米特（Hermite）出版了《论指数函数》（Sur la fonction exponentielle），其中他证明了e是超越数。

 

1873年

吉布斯（Gibbs）发表了两篇关于热力学图的重要论文。

 

1873年

布罗卡尔（Brocard）做出了他的关于三角形的工作。

 

1874年

康（Cantor）发表了他的第一篇关于集合论的论文。他严格描述了无穷的概念。他证明了无穷有不同的大小。他还证明了一个引起争议的结果：几乎所有的数都是超越数。

 

1876年

吉布斯（Gibbs）出版了《关于多相物质平衡》（On the Equilibrium of Heterogeneous Substances），它代表了数学在化学中的主要应用。

 

1877年

康托发现了一个惊奇的事实：区间[0, 1]的点与一个正方形内的点存在一一对应。

 

 

1878年

西尔维斯特（Sylvester）成立了《美国数学杂志》。

 

1879年

肯培（Kempe）发表了他对四色定理的错误证明。

 

1879年

雷克西斯（Lexis）出版了《统计序列的稳定性理论》（On the theory of the stability of statistical series），开始了时间序列的研究。

 

1879年

哈尔科夫数学协会成立。

 

1880年

庞加莱（Poincaré）发表了关于自守函数的重要结果。

 

 

1881年

韦恩（Venn）引入了“韦恩图”，它成为集合论的有用工具。

 

1881年

吉布斯（Gibbs）在为他学生写的小册子中发展了向量分析。这种分析方法在麦克斯韦对电磁波的数学分析中有重要作用。

 

1882年

林德曼（Lindemann）证明了π是超越数。这就证明了用尺规不可能作出一个正方形使得与给定的圆有相同面积。化圆为方这个古典问题可以追溯到古希腊时期，多个世纪以来成为数学思想发展的驱动力。

 

1882年

米塔-列夫勒（Mittag-Leffler）建立了《数学学报》（Acta Mathematica）。

 

1883年

雷诺（Reynolds）出版了《决定水流为直线或曲线运动的条件以及在平行水槽中的阻力定律的探讨》(An experimental investigation of the circumstances which determine whether the motion of water in parallel channels shall be direct or sinuous and of the law of resistance in parallel channels)。书中出现了用于流体力学建模的“雷诺数”。

 

1883年

庞加莱发表了一篇论文，开启了多复变解析函数理论的研究。

 

1883年

爱丁堡数学学会成立。

 

1884年

沃尔泰拉（Volterra）开始了积分方程的研究。

 

1884年，弗雷格（Frege）出版了《算术基础》（The Foundations of Arithmetic）。

 

1884年

赫尔德（Hölder）发现了“赫尔德不等式”。

 

1884年

米塔-列夫勒（Mittag-Leffler）出版了《单变量函数的解析表示》（Sur la représentation analytique fes fonctions monogènes uniformes d'une variable indépendante），给出了他关于指定极点和奇异部分的亚纯函数构造的理论。

 

1884年

弗罗贝尼乌斯（Frobenius）对于抽象群证明了西罗定理。

 

1884年

里奇-库尔巴斯托罗（Ricci-Curbastro）开始了关于绝对微积分（absolute differential calculus）的工作。

 

1884年

巴勒莫数学会（Circolo Matematico di Palermo）成立。

 

1885年

魏尔斯特拉斯证明实数轴的有限闭区间上的连续函数可以用多项式任意一致逼近。

 

1885年

埃奇沃斯（Edgeworth）出版了《统计方法》（Methods of Statistics），其中阐述了对于均值比较的显著性检验的应用和解释。

 

1886年

雷诺阐述了润滑的理论（雷诺润滑方程）。

 

1886年

皮亚诺（Peano）证明了如果f(x, y)连续，那么一阶微分方程dy/dx = f(x, y)有解。

 

1887年

列维-齐维塔（Levi-Civita）发表了一篇论文，发展了张量微积分。

 

1888年

戴德金出版了《数的本质和意义》（Was sind und was sollen die Zahlen）。他将算术建立在严格的基础上，这个基础被称为“皮亚诺公理”。

 

1888年

高尔顿（Galton）引入了相关系数的概念。

 

1888年，恩格尔（Engel）和李（Lie）出版了三卷本《变换群理论》（Theorie der Transformationsgruppen）的第一卷，它是关于连续变换群的重要著作。

 

1889年，皮亚诺（Peano）出版了《算术原理》（Arithmetices principia, nova methodo exposita），通过集合来定义自然数的方式给出了皮亚诺公理，。

 

1889年

菲茨杰惹（FitzGerald）提出了洛伦兹-斐兹杰惹收缩来解释“迈克耳孙-莫利实验”。

 

1890年

皮亚诺发现了空间填充曲线。

 

1890年

圣彼得堡数学学会成立。

 

1890年

希伍德（Heawood）出版了《地图颜色定理》（Map colour theorems），他指出了肯普（Kempe）对四色定理的证明的错误。他证明了五种颜色是足够的。

 

 

1891年

费多洛夫（Fedorov）和申费里斯（Schönflies）独立地对晶体学空间群进行了分类，证明了一共有230 种类。

 

1892年，庞加莱出版了三卷本《天体力学的新方法》（Les Méthodes nouvelles de la mécanique céleste）的第一卷。他旨在完全刻画机械系统的所有运动，援引流体流动的类比。他还证明，以前例如德劳内（Delaunay）用于研究三体问题的级数展开是收敛的，但一般不是一致收敛。这使人怀疑拉格朗日和拉普拉斯给出的关于太阳系稳定性的证明。

 

1893年

皮尔逊（Pearson）发表了一系列论文中的第一篇，在此后18年共发表了18篇论文，引入了大量基本概念来研究统计学。这些论文包含了对回归分析和相关系数的贡献，以及对统计显著性的卡方检验。

 

 

1894年

庞加莱开始了代数拓扑的工作。

 

1894年

博雷尔（Borel）引入了“博雷尔测度”。

 

1894年

嘉当（Cartan）在他的博士论文中对复数域上所有有限维单李代数进行了分类。

 

1895年

庞加莱出版了《位置分析》（Analysis situs），这是他的第一本拓扑学著作，给出了这个专题的较早的系统性处理。他是代数拓扑的创始人，发表了这个专题的6篇论文。他引入了基本群。

 

1895年

康托（Cantor）发表了关于超穷算术的两篇重要论文的第一篇。

 

1895年

安里西·韦伯（Heinrich Weber）出版了他的著名教科书《代数讲义》（Lehrbuch der Algebra）。

 

 

1896年

素数定理分别由阿达玛（Hadamard）和法勒布赛（de la Vallée-Poussin）独立地证明。这个定理给出了不超过一个给定数的素数个数的估计，证明了当n趋于无穷时，不超过n的素数个数趋向于n/log n。

 

1896年

切萨罗（Cesàro）出版了《内蕴几何学教程》（Lezione di geometria intrinseca），其中他阐述了内蕴几何。

 

1896年

弗罗贝尼乌斯（Frobenius）引入了群特征标。

 

1897年

亨泽尔（Hensel）发明了p进数（p-adic numbers）。

 

1897年

布拉利-福尔蒂（Burali-Forti）是第一个发现集合论悖论的人。

 

1897年

伯恩赛德（Burnside）出版了《有限阶群理论》（The Theory of Groups of Finite Order）。

 

1897年

弗罗贝尼乌斯开始研究群表示论。

 

1898年

弗罗贝尼乌斯引入诱导表示的概念以及“弗罗贝尼乌斯互反定理”。

 

1898年

阿达玛关于负曲率曲面上的测地线的工作为符号动力学奠定基础。

 

1899年

希尔伯特（Hilbert）出版了《几何基础》（Grundlagen der Geometrie），将几何建立在形式公理之上。

 

 

1899年

李亚普诺夫（Lyapunov）提出了方法来决定常微分方程系统的稳定性。

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

一位杰出的数学家运用物理学中的概念研究了困惑人们数千年的数学问题，并取得了进展。

 

 

数学里面充满了超自然的数的系统，其中大部分人从来没有听说过，甚至理解起来有困难。但是有理数是家喻户晓的，它们是自然数和分数——这些有理数你从小学就知道了。但是对于数学家来说，最简单的问题往往最难理解。它们简单的就像一堵抗风墙，没有裂缝、突出物或者明显你可以抓住的某些东西。

 

牛津大学的一位叫金明迥的数学家，对于寻找哪些有理数可以解特定类型的方程特别感兴趣。几千年来无数数论学家挑战过这个问题。他们在解决问题方面进展甚微。当一个问题研究了很久却没答案，我们很自然的就认为唯一的出路就是有一个人能提出新的想法。这个人就是金明迥。

“即使我们已经研究了3000年，但研究这些问题依然没有太多的技术手段。所以任何人无论何时提出一个可靠的新方法去解决它都是一个大的进展，这就是金明迥所做的。”威斯康星大学的数学家乔丹·艾伦伯格（Jordan Ellenberg）评论道。

 

在过去的十年间，金明迥想出了一个非常新颖的方法----在看似无规律的有理数域寻找模式。他将这种方法写进论文里，发布在讨论会中，并将其传递给学生，现在学生们自己继续进行研究。但是他一直保留着一些东西， 他的思想正走向成熟，不是基于纯粹的数论，而是从物理中借用概念。对于金明迥来说，有理数解多少有点像光的轨迹。

 

如果这样的联系让你觉得像天方夜谭，那就对了，因为一些数学家也甚至和你有相同想法。由于这个原因，金炯明长期以来没有吐露这个想法。“我将它藏了起来，因为一直以来我多少会因为物理联系而不安，”他说。“数论学者是一群相当严谨刻板的人，物理的因素的加入有时使他们更加怀疑我做的数学。”

 

但是现在金明迥说他已经打算向世人表达他的想法。“我想这个改变单纯的是因为思想成熟起来了！”53岁的金明迥在我们交流这个故事的一封邮件的开头写到。

 

他最近已经举办了一场学术会议，邀请了数论学家和弦论学家。他也为还没有习惯于通过直接类比物理世界来思考数论问题的数学界写一篇文章去描述他的想法。

 

至今仍有一个绊脚石——数学和物理类比的最后一部分，金明迥仍需要继续攻克下去。他希望邀请更多的人去参与他的研究，特别是物理学家，他需要物理学家的帮助去完善它。

 

一个古老的挑战

 

方程的有理解深深地吸引着人们。找到方程的有理解，就像拼图块完美地落实到对应的位置那样令人满足。基于这样的理由，数学中很多著名的猜想都是关于方程有理解的。

 

有理数包含整数和任何可以表示为两个互素的整数之比的数。例如1，-4以及99/100.数学家对丢番图方程（Diophantine equation）——整系数多项式方程的有理数解特别感兴趣。就像x²+y²=1。公元3世纪，生活在古希腊亚历山大城的丢番图就研究了很多这样的方程。

 

有理解很难用全面的方法所找到，因为他们不遵循任何几何模式。考虑方程x²+y²=1。它的实数解是一个圆，拿走在这个圆上的所有不能表示为分数的点，所留下的就是有理解，而这样的解不会形成一个规则的形状。有理解是随机分布在圆周上的。

 

 

 “具有有理坐标点的条件根本不是几何条件。 你无法知道如果一些有理点满足某方程，它必须满足写什么条件”金明迥说。

 

有的方程，通常容易找到某个单一的有理解，甚至许多有理解。但对于不喜欢松散结果的数学家来说，他们对研究所有的有理解更有兴趣。这样问题就会难很多了。事实上，甚至是关于有理数最直白的结果，足以让你在数学圈出人头地。如同在1986年，一个名叫法尔廷斯(Gerd Faltings)的数学家荣获了数学最高荣誉的菲尔兹奖，他就是解决了一个叫莫德尔猜想(Mordell conjecture)）的问题，证明了一族特定的丢番图方程仅有有限多的有理解（而不是无限多解）。

 

法尔廷斯的证明在数论中是一个具有举足轻重的结果。但这也是数学家所说的“无用的证明”，事实上这意味着它没有精确计算出有理解的数量，更不用说找出它们了。从那以后，数学家开始寻找解决下一步的方法。有理点看起来就像一个方程的普通图像上的随机点。如果他们改变他们所研究问题的条件，数学家们希望这些点将看起来像一个星座一样，他们能以一些精确的方式去描述。但问题是，在已知的数学领域并没有给出这样的条件。

 

 “为了得到关于有理解的有效结果，人们当然会认为，解决这个问题需要一个全新的想法。”艾伦伯格说。

 

目前，关于新想法是什么样，有两个主要研究。一个来自于日本数学家望月新一，2012年，他在京都大学的教职员网页上发表了数百页复杂又新奇的数学成果。五年后，他的论文依然是高深莫测的。而另一个新想法就来自于金明迥。他试图在扩张的数论空间中思考有理数，在这其中隐藏的模式开始出现。

 

一个对称解

 

数学家通常说研究对象的对称性越好，就越容易研究。鉴于此，他们希望将丢番图方程的研究置于比问题本身产生的空间更对称空间中。如果他们能这样做，他们可以利用新的相关对称性去追踪他们所寻找的有理点。

 

为了见识一下对称性如何帮助数学家解决问题，画一个圆。可能你的目标是定义在圆上的所有点。对称性是一个有用的工具因为它创建了一个映射，可以让你从已知点的性质推出未知点的性质。

 

想象一下，你已经在下半圆找到了所有的有理点。因为圆是反射对称的，你可以水平直径为对称轴翻转下半圆的有理点(改变所有y坐标的符号)，于是一下子你就可以得到在上半圆的所有有理点。事实上，一个圆拥有丰富的对称性，即使知道一个单点的位置，结合对称知识，如果你需要找圆上的所有有理点，只要围绕原点无限旋转对称就可以得到。

 

但是如果你处理的几何对象有着高度无规律性，就像一个随机游走路径，你将需要努力去分别独立找出每一个点——这儿没有对称关系帮助你去将已知点映射到未知点。

 

数的集合也可以拥有对称性。集合的对称性越多，就越容易去理解——你可以应用对称性去发现未知的值。具有特定类型对称关系的数聚在一起形成一个“群”，数学家可以使用群的性质去理解包含在其中的所有的数。

 

一个方程的有理解集合不具有任何对称性也不形成一个群。从而使数学家们不可能一次性就发现所有的解。

 

从二十世纪40年代开始，数学家们开始探索一种方法去将丢番图方程的解放到一个拥有更多对称性的空间中去找。数学家沙博蒂(Claude Chabauty)发现在他构建的更大的几何空间的内部（通过一个被称为p进数（p- adic numbers）的扩张的全域），有理数形成了自己的对称子空间。他开始用这样的子空间与丢番图方程的图像联系起来。两个空间相交的点就是方程的有理解。

 

在二十世纪80年代，数学家科尔曼(Robert Coleman)对 沙博蒂的结果进行了改进。 在那之后的几十年里，科尔曼-沙博蒂方法成为数学家寻找丢番图方程有理解最有效的工具。但只有当方程的图像与更大的空间大小成比例时，它才起作用。当不成比例时，那么就很难精确找出方程曲线与有理数相交的点。

 

“如果你有一条曲线在空间内，而且有太多有理点，这些有理点集纠结在一起，你就很难区分哪些有理点在曲线上。”一位在加州大学圣地亚哥分校名叫凯德拉亚（Kiran Kedlaya）的数学家说。

 

于是，金明迥开始着手起这个问题了。为了在沙博蒂的基础上取得更进一步的成果，他希望去寻找一个甚至更大的空间去思考丢番图方程——一个有更多有理点分布的空间，于是他就可以研究更多不同种类丢番图方程的相交点。

 

空间的空间

 

如果你在寻找一个更大的空间，以及在思考如何沿着对称这条线索来寻找答案，借助于物理办法是个好的选择。

 

一般来说，在数学的意义上，一个空间是一个拥有几何或拓扑结构的点集。随意分散的一千个点不会形成空间，因为没有任何结构将他们联系在一起。但是对于一个球，由特殊的连续分布的点构成，它是一个空间。同样的环面、二维平面、或者我们生活中四维时空也是一个空间。

 

除了这些空间外，存在更多的风格迥异的空间，你可以把它看成“空间的空间”。举一个非常简单的例子，想象你有一个三角形——这是一个空间，那么继续想象所有可能的三角形，它们组成一个空间。在这个更大空间内的每一点代表一个特定的三角形，由它所表示的三角形的角的顶点的坐标。

 

这样的想法在物理中非常有用。在广义相对论的框架下，时间和空间不断演变，物理学家把每个时空看作是所有时空所组成的空间中的一个点。空间的空间在规范场论这个物理领域中出现过，这与物理学家在物理空间之上建立的场有关。这些场描述了你在空间中运动时，这些力如何起作用，如同你看到的电磁力和重力一样。你可以想象，在空间的每一个点上，这些场的构造都略有不同——而且所有这些不同的构造聚在一起形成了更高维度的“所有场的空间”中的点。

 

这个物理学中场的空间与金明迥在数论中提出的观点类似。为了便于理解，我们考虑一束光。物理学家想象光穿过高维的场空间。在这个空间中，光线将遵循“最小作用量原理”的路径——也就是从A到B所需最短时间的路径。这个原理解释了为什么当光从一个介质到另一种介质会弯曲——弯曲的路径花费的时间最少。

 

物理学中出现的这些更大的空间的空间具有额外的对称性，这些对称性并不存在于它们所代表的任何空间中。通过对称性可以找出特殊点，例如强调的时间最短路径。在另一种情况下以另一种方式构建，这些相同类型的对称可能会注重其他类型的点——如对应于方程的有理解的点。

理学中出现的这些更大的空间空间具有额外的对称性，这些对称性并不存在

 

对称性与物理之间的纠缠

 

数论没有粒子可以追踪，但是数论多少有点像时空，为此它也提供了一种寻找所有可能的路径方法和构建对所有可能路径的空间。从这种基本的对应中，金明迥提出了一种方案：寻找光的轨道以及探寻丢番图方程的有理解是同一个问题的两个方面.正如他在德国海德堡举行的数学物理会议上解释的那样。

 

丢番图方程的解形成空间是由方程定义的曲线。这些曲线可以像圆一样是一维的（一维流形），或者他们可以是更高维的空间。例如，如果你试图寻找丢番图方程———x^4+y^4=1的复解，你就得到了一个三孔环面。在这个环面上的有理解缺乏几何结构，这样就很难去找到他们，但是它们可以被做成对应于具有结构的空间的更高维空间中的点。

金明迥通过考虑可以在环面上绘制环的方式（或等式定义的任何空间）来构造空间的高维空间。绘制环的过程如下：首先，选择一个基点，然后从该点绘制一个环到任何其他点，然后再返回。重复这个过程，画出连接基点和圆环面上其他点的路径。最后，你会有一个所有可能的环，他的起始点和结束点都在基点。这种环的集合是数学中一个重要的中心对象，它被称为空间的基本群。

 

​

 

你可以使用在环面上的任何点作为你的基点。每一个点将有一个独一无二错综复杂的路径。每一个这些路径的集合可以被表示为一个点在一个更高维的“路径集合的空间”（就像所有的可能的三角形的空间）。这个空间的几何上非常类似于物理学家在规范场理论中构造的“空间空间”。当从一个点移动到环面上另一个点时，路径集合的变化非常类似于在实际空间中从一个点移动到另一个点时场变化的方式。

 

空间的空间具有额外的对称性，不表现于环面本身。虽然环面上的有理点之间没有对称性，但如果你进入所有路径集合的空间，就可以找到与有理点相关的点之间的对称性。这样你可以得到之前所看不见的对称性。

 

“我时常用到的一个短语是这些路径中有一种“隐藏的算术对称性”，高度类似于规范场论中内在的对称性”金明迥说。

 

 

就像沙博蒂所说的那样，金明迥通过考虑在他所构造的更大的空间结构中交叉的点去寻找有理解，同时运用这个空间中的对称性去限制空间中的交叉点。他希望建立一个方程去精确的找到这些点。

在物理环境中，你可以想象光线可能会采取的所有可能的路径。这是你“所有路径的空间”。在这样的空间中，引起物理学家兴趣的是与时间最小化路径相对应的点。金明迥认为寻找有理点的过程与错综复杂的路径对应的点具有同样的性质——也就是说，当你开始思考丢番图方程的几何形式时，这些点将最小化某些性质。只是他还没有找出这种性质是什么。

“我开始寻找的东西是一个在数学环境中的最小作用量原理，他在邮件中写道。“我还是不太清楚，但我有信心，它就在那里，我能找到它。”

 

​

 

一个不确定的未来

 

在过去的几个月 ，我对几位数学家描述了金明迥由物理所启发的想法，他们都仰慕金明迥对数论的贡献。然而，当把金明迥遇到的困难传达给他们时，他们并不知道该如何下手。

 

“作为一个具有代表性的数论学家，如果你向我展示了金明迥一直在做的所有的这些“恐怖”的事情，并问我是否受到灵感启发，我会说'你到底在说什么鬼话？'”艾伦伯格如是说。

 

至今，金明迥并没有在他的论文中提及物理学。取而代之的是，他把他的目标称为Selmer簇,他考虑Selmer簇在所有Selmer簇空间中的关系。这些对于数论学者来说是可识别的术语。但是对于金明迥来说他们一直是物理学中某些物体的另一个名称。

 

“利用物理学中的思想去解决数论中的问题是有可能的，但是我还没有想好如何建立起这样的框架，”金明迥说，“我们在一个关键点上，对物理的理解足够成熟，以及有足够多的数论学者对这个问题感兴趣，所以接下来我们需要进一步推进。”

阻碍推进金明迥的方法一个困难在于在所有错综复杂的圈所组成的空间中寻找一些最小作用量的类型。在物理世界中，这样的观念十分自然，但是在算术中并不那么显然。甚至是对金明迥的工作了解最深的数学家，也非常关心他是否会找到它。

 

“我认为金明迥的工作将会给我们带来许多有价值的东西。我不认为我们要像金明迥想要的那样清晰的理解有理解所在的地方是某种算术规范场理论（arithmetic gauge theory）的经典解”哈佛大学数学物理教授阿尔纳夫·特里帕蒂说。

 

今天，物理学的语言几乎完全在数论的实践之外。金明迥认为这种情况肯定会改变。40年以前，物理和几何、拓扑的研究几乎都是独立。但在20世纪80年代，屈指可数的几位数学家和物理学家建立了有效的方法，该方法运用物理去研究形状的性质，现在这些学者都是领军人物了，而且该领域从未停止向前。

 

“如今不了解物理学几乎不可能对几何学和拓扑学感兴趣。我有理由确信在数论上也会有这种情况发生”在接下来的15年，金明迥说，“这样的联系将变得十分自然。”

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

原文作者，David Austin，大峡谷州立大学。

翻译作者，小涟猫，哆嗒数学网翻译组成员。

校对，333。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

下面这张图片以矩阵形式包含了3871488个像素。每个像素的颜色由红绿蓝分量决定，每种颜色占一字节内存，我们可能想当然地认为，这个图片会占11614464字节内存，但是这个JPEG 文件实际只占734268字节内存，约为原来十六分之一。下面我们将会介绍这种由联合图像专家小组（JPEG）开发的高效图像压缩算法。

 

 

相比专门使用红绿蓝三种颜色分量，用另外三种不同的分量来描述会更方便:亮度Y, 与颜色明亮程度密切相关；C_b、C_r为蓝色、红色色度分量，它们可以粗略地确定一个色彩。上述两种表示方法可以通过一个可逆的仿射变换实现相互转换。例如，为重新获得红、绿、蓝分量的值，我们可以用以下公式：

可以看出，亮度与三种基本颜色分量的作用相同。为了可视化这个变换，我们保持亮度不变并且混合各类色度值得到以下颜色

 

 

这个算法将图片分割为8*8的可单独处理的图像块，这是一个样本模块。

在我们的样本模块中，（Y，C_b，C_r）三种分量的分布情况如下，明亮的区域对应更大的数值。

可以看出亮度值Y产生的是原图的灰度图。心理可视化实验表明，人眼对亮度变化最为敏感，因此对颜色转换时可以把最重要的信息压缩到单个分量中。彩电使用相似的颜色模型，它能让黑白电视也可以有效播放貌似彩色效果的图像。

 

原因稍后解释，现在我们用一些频率越来越块的余弦函数的线性组合求表示各个分量值。例如，如果Y_ x,y 代表图像块中的第x 行，第y 列的方块处的亮度，就可以表示为

归一化常数C_u,v 不需过分关注; 系数F_u,v由二维离散余弦变换（DCT）得到，而对于它的高效计算则可以采用快速傅立叶变换（FFT）。

大多数图像块的分量值不会急剧改变，人眼对这些变化也不是很敏感，因此，频率较高的DCT 变换系数可能很小甚至忽略也不影响对我们对于图像的感知。这样的观察启迪了我们，也许可以以整数的形式来量化DCT的系数并加以存储。

 

量化过程涉及两个要素。第一个为参数α，它由使用者选择，用于控制压缩程度与图片质量。α值越大，文件越小，图片质量也就越差。

 

第二个因素是一个8*8的矩阵Q=[Q_u,v]，其中的系数为对F_u,v /αQ_u,v取整后的值, 依经验选取Qu,v时，为了弱化高频的影响，通常对于高频部分赋予较大的数值。例如，一个用于量化亮度离DCT系数的矩阵为

考虑到亮度携带更多重要的视觉信息，所以我们用不同的矩阵来分别量化描述亮度的系数与描述色调的系数。用中间值α处理我们的样本图像块，量化后的亮度系数如下

量化后的系数按照箭头指向排序，低频排在前面。

样本的亮度分量，其量化后的系数为数列 7, -2, 4, 1, 0, 1, 0, 1, -1以及55个0。相比存储这么多数字零，我们直接记录零的个数，这样极大减少了存储需求。后续的压缩要依靠哈夫曼编码来实现系数数列的高效效存储。

图像的重建可以通过逆过程实现。量化系数给出了F_u,v的近似值，这些反过来又给出了Y, C_b , C_r和R,G,B 分量的值。下图中左图表示原图，右边则是重建后的图。

DFT似乎比DCT 更好用，因为它易于计算。但是我们却选择了DCT，这是因为我们希望把信息尽量集中到频率较低的系数上。以8*8模块中的某一行Y_x的值为例, DFT方法将Y_x表示为一些周期为8的函数的线性组合，并由此给出了Y_x的一个周期延拓。但该变换非常不必要地将 y_7 与 y_8 = y_0之间的变化也记录下来了，这就导致了高频分量的加入以及由此产生的显著影响。在下面的图中，Y_x 值用黑色表示，而由傅立叶变换的三个最低频项所给出的近似值是用红色表示的。

   
   与之相比，DCT方法将Yx表示为一些周期为16且关于x=7.5对称的函数的线性组合。这使得Y_x的近似延拓更为平滑，从而减少了对高频分量的依赖。下图是DCT所给出的近似值，注意到近似效果得到了显著改善。

因为这些8*8图像块都是被独立处理，所以这就导致了在高压缩率的情况下边缘部分的不连续性变得十分明显。除此之外，我们通常还希望用中等分辨率就能高效重建图像。这些因素以及一些其他原因，促使了JPEG2000压缩算法的产生。在诸多不同点中，JPEG2000还采用离散小波变换代替了DCT

JPEG2000算法把图像分割为尺寸更加精细的图像块，比如256*256。为了演示小波变换，取图像块中的一行像素并令y_x 代表该行中的某一个值。现在求小波系数。

h_x为能够检测到高频变化的高通系数，l_x为低通系数。按照低通系数在前高通系数在后的顺序进行排序，对列也做相同处理后，可得小波系数的数表。

   
位于LL子块中的系数是通过对所有2*2的邻近像素点取平均值得到的因此代表了一个低分辨率的图像。另外三个子块描述了当重建高分辨率图像时所必要的变换。我们对LL子块重复之前的处理，从而实现以越来越低的分辨率存储图像。

量化的过程会检测数值变化不明显的区域，从而可以安全地忽略高通系数。和之前介绍的小波变换求取两个相邻值的平均值不同的是，JPEG2000算法使用Cohen-Daubechies Feauveau (9, 7) 小波变换，它可实现取邻近九个值的平均值，这样可令图像更加平滑。

 

JPEG2000的算法复杂度比JPEG高一个数量级，而且在中、低压缩率时，图像质量并没有优化多少。但是在高压缩率情况下，JPEG算法采用的8*8图像块会导致图片质量严重下降，而JPEG2000的效果此时会明显更好。

因为JPEG2000在获取同等质量图像时更为费劲，所以它对JPEG来说并没有明显优势。事实上，目前只有少数网站支持显示JPEG2000图像。它的优势在于，当处于增加算法复杂度不再是问题的环境下，可以为图像提供灵活的格式。

例如利用小波变换能以不同分辨率有效重组图像，用户可肉眼迅速大量搜索低分辨率的图片。JPEG2000允许用户指定区域以高分辨率展示，通常是出于医学成像的需要。最后，它也使得数码图像能以JPEG2000的格式存储在相机内存卡中，这样在拍照后，图片会以低分辨率存储起来以减少内存使用。在JPEG面世约十年后，JPEG2000才出现。它还拥有一些其他的功能特性，比如事后图像加密的功能。

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

原文作者，Devin Pope，行为科学家。

翻译作者，孙云龙，哆嗒数学网翻译组成员。

校对，mathyrl。。

 

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

一位前谷歌工程师最近提醒了世人，在包括物理、计算机科学和工程学在内的几个数理领域中，女性的比例不足。

造成这一比例偏低的原因引起了激烈的争论，广泛讨论认为进入门槛和考试成绩的性别差异是潜在原因。

 

 

但新的数据分析却强调了信心在差距中的重要性。

一些年轻女性, 包括在数学方面特别有天赋的, 往往都会低估自己的能力。

缺乏信心可能会促使这一领域的一些最好的人才去寻求其他成功途径，毕竟, 即使一些人有过人的天赋, 如果她不相信自己是一个天才的数学家, 她也不太可能去喜欢科学、技术、工程、数学的学习生涯，并且以后以此为生。

(顺便说一下, 一些女性发现她们的自信也会受到舆论宣称女性容易成为次等数学家的言论的影响, 但这都是以后的事情了。)  

最近, 我偶然发现了一些数据，在我们都特别熟悉的SAT考试中印证了上述观点

当一些高中生们在参加 SAT测试时, 他们都会填写一份人口统计学和其他高中和大学有关问题的问卷。这个问卷的老版本会询问学生对他们自己智力能力的信心。具体来说, 学生们会被问及，他们是否相信自己是数学能力最高的前10%。

使这个设定变得特别有趣的是, 数据不仅包括学生们对自己能力的信心, 还包括他们的 SAT 分数, 而这个分数为实际能力提供了大致的衡量标准。在九十年代末和二十一世纪初, 样本调查使用了超过 400万 SAT 考生的数据, 下图显示了，实际SAT数学成绩每10分为间隔，在每个分数段中相信自己的数学能力排在前10%的男性和女性的比例。

如人所料, 如果学生在SAT数学部分的分数更高 (图中的曲线是向上倾斜的), 他们更有可能相信自己在10%。然而, 这个图表明, 在所有的 SAT 分数水平, 男性比女性对自己的数学能力更有信心。例如, 这个图表明, 达到了700分的男性有67%相信他们的数学能力在前10%, 而女性达到700分的却只有56%的人有相同的信念。这些结果表明, 女性对自己的数学能力的信心是不及相同SAT 数学成绩的男性的。

一些人可能会说，这个数据不能说明只在数学学科存在这个性别差异，有可能在所有学科都存在这种差异。幸运的是, 数据能够说明，男性比女性更自信到底是一个普遍现象，还是在数学学科中有一些特殊的数据表现。

下图显示了大约 400万SAT考生对通过他们的SAT语文分数他们是否相信自己的写作能力在10%这个问题的回答，不像数学能力图表, 在这里我们可以明显看到, 在取得相同 SAT 成绩时，女性比男性对自己的写作技巧更有信心。因此, 不是在所有科目中, 男性都比女性更有信心。相反, 数学能力似乎是一个特殊的学科, 男性和女性表现出信心上的巨大差别。
 

 

这些数据在一个熟悉的领域给人提供了令人信服的证据, 证明了即便能考出相同的分数，男性和女性在数学能力上的自信程度也是存在差异的。这些信心的差异可能是造成大学专业学生和职业人员中性别失衡的一个重要因素。精准的在提高数学信心上做工作, 或许是科学、技术、工程、数学内解决性别失衡方面问题的一项重要手段。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

 

原文作者，圣安德鲁斯大学数学与统计学院。

翻译作者，mathyrl，哆嗒数学网翻译组成员。

校对，math001。

  

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa

 

 

从今天起，我们将连载这部数学编年史。本文是翻译版本，因为工作量巨大，必有疏漏（包括原文也会有错误），欢迎指正。

 

这应该是网上最全的数学编年史，从公元前30000年到公元2000年，哆嗒数学网为你奉献。

 

 这里是 数学上下三万年（五）：十九世纪上半叶的数学

 

这个时期欧美基本完成工业革命，各种科学学科开始按现代的门类分化，并影响到社会学科。中国也在这个时期进入半殖民地半封建社会。

  

本期出场人物有：高斯、勒让德、热尔曼、傅里叶、泊松、拉普拉斯、柯西、阿贝尔、哈密顿、狄利克雷、洛巴切夫斯基、雅克比、刘维尔、德摩根、埃尔米特等。

 

 

本系列下面是往期内容：

 

数学上下三万年（一）：爱在西元前

 

数学上下三万年（二）：从罗马时代到中世纪

 

数学上下三万年（三）：大航海时代

 

数学上下三万年（四）：欧洲资产阶级革命开启

 

 

 

1800年，拉克鲁瓦（Lacroix）完成了他的三卷本教科书《微分学与积分学》（Traité de Calcul differéntiel et intégral）的出版。

 

1801年

高斯出版了《算术研究》（Disquisitiones Arithmeticae）。它包含了七部分，前六部分研究数论，最后一部分研究正十七边形尺规作图。

 

 

1801年

谷神星被发现然后不知所踪。高斯从少量已有的观测资料计算了它的轨道，随后几乎恰好在高斯预测的位置上谷神星被重新发现。

 

1801年

高斯证明了费马的猜想，即每个正整数可以表为三个三角数之和。

 

 

1803年

拉扎尔·卡诺（Lazare Carnot）出版了《位置几何学》（Géométrie de position），其中首次在几何学中系统地使用了向量。

 

1804年

贝塞尔（Bessel）发表了一篇关于哈雷彗星轨道的论文，其中使用了200年前哈里奥特的观测数据。

 

1806年

阿尔冈（Argand）引入了阿尔冈图作为在平面上复数几何表示的一种方法。

 

1806年

勒让德发展了最小二乘法，用于寻找一组数据的最佳逼近。

 

1807年

傅立叶（Fourier）发现了用一系列三角函数之和来表示连续函数的方法，并在一篇提交到法国科学院的论文《固体上的热传导》（On the Propagation of Heat in Solid Bodies）中使用了这个方法。

 

 

1808年

热尔曼（Germain）对费马大定理作出了重要贡献。这就是被勒让德命名的“热尔曼定理”。

 

1809年

潘索（Poinsot）发现了两个新的正多面体。

 

1809年

高斯描述了最小二乘法，在《天体运动论》（Theoria motus corporum coelestium in sectionibus conicis Solem ambientium）中他使用这种方法寻找天体的轨道。

 

1810年

葛尔刚（Gergonne）出版了他的新数学期刊《纯粹数学与应用数学年刊》（Annales de mathématique pures et appliquées）的第一卷，这个期刊又称为《葛尔刚年刊》（Annales de Gergonne）。

 

1811年

泊松（Poisson）出版了《力学》（Traité de mécanique）。它包含了泊松关于数学在电磁学与力学的应用的研究工作。

 

1812年

拉普拉斯（Laplace）出版了两卷本《概率的解析理论》（Théorie Analytique des probabilités）。第一卷研究了生成函数以及概率论中出现的各种表达式的逼近。第二卷包含了拉普拉斯的概率定义、贝叶斯法则与数学期望。

 

1814年

阿尔冈（Argand）给出了对代数基本定理的一个漂亮证明（带有一些缺陷）。

 

1814年

巴洛（Barlow）制作了巴洛表，给出了从1到10000的整数的因子分解、平方、立方、平方根、倒数和双曲线对数。

 

1815年

彼得·罗热（Peter Roget，《罗热同义词词典》的作者）发明了对数计算尺。

 

1815年

普法夫（Pfaff）发表了关于被称为“普法夫形式”的重要工作。

 

1816年

皮科克（Peacock），赫歇尔（Herschel）和巴贝奇（Babbage）是剑桥分析学会（Analytical Society）的领袖，该学会出版了拉克鲁瓦（Lacroix）的教科书《微分学与积分学》（Traité de Calcul differéntiel et intégral）的英译本。

 

1817年

贝塞尔在研究开普勒问题过程中发现了一族被称为“贝塞尔函数”的整函数，以确定三体在相互引力的作用下的运动。

 

1817年

波尔查诺（Bolzano）出版了《纯分析证明》（Rein analytischer Beweis），试图将微积分从无穷小量概念中解放出来。他不使用无穷小量来定义连续函数。这本著作包含了波尔查诺-魏尔斯特拉斯定理。

 

1818年

受到拉普拉斯工作的启发，亚德里安（Adrain）发表了地球形态以及不同纬度的重力的研究。

 

1819年

霍纳（Horner）向皇家学会提交了一篇论文，给出了用于求解代数方程的“霍纳方法”，该论文于同年发表在英国皇家学会哲学汇刊。

 

1820年

布利安香（Brianchon）发表了《在给定四个条件下，确定等边双曲线的研究》（Recherches sur la determination d'une hyperbole equilatère, au moyen de quatres conditions données），其中包含了九点圆定理的陈述和证明。

 

1821年

纳维对于不可压缩流体给出了著名的“纳维-斯托克斯方程”。

 

1821年

柯西（Cauchy）出版了《分析教程》（Cours d'analyse），这是第一次将数学分析建立在正式基础上。它为巴黎综合理工学院的学生设计，致力于尽可能严格地发展微积分的基本定理。

 

 

1822年

彭赛列（Poncelet）在《论图形的射影性质》（Traité des propriétés projectives des figures）发展了射影几何的原理。这本著作包含了射影几何的基本思想，例如交比、透视、对合、以及虚圆点。

 

1822年

傅立叶（Fourier）1811年的获奖作品《热的解析理论》（Théorie analytique de la chaleur）发表。它使得傅立叶分析的技术被广泛地利用，这将广泛应用于数学和整个科学领域。

 

1822年

费尔巴哈（Feuerbach）发表了他的关于三角形的九点圆的发现。

 

1823年

鲍耶·亚诺什（János Bolyai）完成了关于非欧几何的一个完整体系的论文的准备工作。当鲍耶发现高斯已经预见到他的大部分工作但没有发表任何东西，他推迟了发表。

 

1823年

巴贝奇（Babbage）开始制造一台大“差分机”，该机器可以计算对数以及三角函数。他的经验来自于他在1819年至1822年间制造的小“差分机”。

 

1824年

萨迪·卡诺（Sadi Carnot）出版了《论火的动力，以及合适的机器来开发这个动力》（Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance）。这是一本关于蒸汽机的书，它在热力学中有根本重要性。形成热力学第二定律的基础的“卡诺循环”也出现在这本书中。

 

1824年

阿贝尔（Abel）证明了高于四次的多项式方程没有根式解。他把这个证明自费出版在一本六页的小册子上。

 

 

1824年

贝塞尔对行星扰动进行研究的同时进一步发展了“贝塞尔函数”。

 

1824年

斯坦纳（Steiner）发展了综合几何学。他在1832年发表了关于这个论题的理论。

 

1825年

冈珀茨（Gompertz）给出了“冈珀茨死亡率定律”，它表明死亡率呈几何级数增长，因此当死亡率以对数标度绘制时，得到一条直线，称为“冈珀茨函数”。

 

1826年

安培（Ampère）出版了《关于电动力学现象之数学理论的回忆录，独一无二的经历》（Memoir on the Mathematical Theory of Electrodynamic Phenomena, Uniquely Deduced from Experience）。它包含电动力定律的数学推导，并描述了四个实验。它为电磁理论奠定了基础。

 

1826年

克雷勒（Crelle）开始出版他的期刊《纯数学和应用数学杂志》（Journal für die reine und angewandte Mathematik），后来被称为“克雷勒杂志”。第一卷包含了阿贝尔的几篇论文。

 

1826年

彭赛列（Poncelet）关于圆锥曲线极点与极线的工作使他发现了对偶原理。引入了术语“极线”的葛尔刚（Gergonne）独立发现了对偶原理。

 

1827年

雅可比（Jacobi）在向勒让德写的信中详述了他关于椭圆函数的发现。与此同时，阿贝尔在独立地进行关于椭圆函数的工作。

 

1827年

莫比乌斯（M?bius）出版了关于解析几何的《重心的计算》（Der barycentrische Calkul）。它成为了经典并包含了他的关于射影几何与仿射几何的很多结果。书中他引入了齐次坐标并讨论了几何变换，特别是射影变换。

 

1827年

费尔巴哈（Feuerbach）写了一篇论文，独立于莫比乌斯引入了齐次坐标。

 

1828年

高斯引入了微分几何并发表了《关于曲面的一般研究》（Disquisitiones generales circa superficies）。这篇论文来源于他对测地线的兴趣，它包含了“高斯曲率”等几何思想。这篇论文也包含了高斯著名的“绝妙定理”（theorema egregrium）。

 

1828年

格林（Green）出版了《论应用数学分析于电磁学》（Essay on the Application of Mathematical Analysis to the Theory of Electricity and Magnets），书中将数学应用于电场和磁场的性质。他引入了术语“势”，发展了势函数的性质，并将其应用于电和磁。连接表面积分和体积积分的公式，现在称为“格林定理”，在书中首次出现，“格林函数”也首次出现在书中，该函数被广泛应用于偏微分方程的解。

 

1828年

阿贝尔开始研究双周期椭圆函数。

 

1828年

普吕克（Plücker）出版了《解析几何》（Analytisch-geometrische），发展了“普吕克简算记号”。他比莫比乌斯和费尔巴哈早一年独立地发现了齐次坐标。

 

1829年

伽罗华（Galois）向法国科学院提交了他的第一篇关于方程代数解的作品。

 

1829年

罗巴切夫斯基（Lobachevsky）发展了非欧几何，特别是双曲几何，他关于这个论题的第一份描述发表在《喀山通讯》（Kazan Messenger）。当它被提交到圣彼得堡科学院时被奥斯特罗格拉德斯基（Ostrogradski）拒绝。

 

约1830年

巴贝奇（Babbage）创建了用于保险计算的第一个精确精算表。

 

1830年

泊松在弹性力学中引入了“泊松比”，其中涉及材料的应力和应变。

 

1830年

皮科克（Peacock）出版了《论代数》（Treatise on Algebra），试图给代数学一个与欧几里德《几何原本》相媲美的逻辑处理。

 

1831年

莫比乌斯（M?bius）发表了《一大类特殊的反转公式》（über eine besondere Art von Umkehrung der Reihen），书中引入了莫比乌斯函数以及莫比乌斯反演公式。

 

1831年

柯西（Cauchy）给出了单复变解析函数的幂级数展开。

 

1832年

斯坦纳（Steiner）出版了《不同几何形式的依赖关系的系统性发展》（Systematische Entwicklungen ...），书中给出了基于度量考虑的射影几何的一种处理。

 

1832年

鲍耶·亚诺什（János Bolyai）关于非欧几何的工作作为他父亲鲍耶·法尔科斯的书的附录发表。

 

1833年

勒让德指出了关于平行公设的12个“证明”中的缺陷。

 

1834年

哈密顿（Hamilton）在《动力学中的一种普遍方法》（On a General Method in Dynamics）使用代数来处理动力学。这篇论文给出了应用于动力学的特征函数的第一个陈述。

 

1835年

凯特勒（Quetelet）出版了《论人类及其能力之发展》（Sur l'homme et le développement de ses facultés）。他提出了“平均人”的概念，认为平均人是根据正态曲线对人类特征测量的中间值。

 

1835年

科里奥利（Coriolis）出版了《物体系的相对运动方程》（Sur les équations du mouvement relatif des systèmes de corps）。他引入了“科里奥利力”，并证明，如果在运动方程中添加一个称为“科里奥利加速度”的额外的力，那么运动定律适用于转动参考系。同年科里奥利出版了一本关于台球的数学理论的著作。

 

1836年

奥斯特格拉斯基（Ostrogradski）重新发现了格林定理。

 

1836年

刘维尔创办了数学杂志《纯粹与应用数学杂志》（Journal de Mathématiques Pures et Appliquées），这份杂志有时被称为《刘维尔杂志》（Journal de Liouville），记录了19世纪法国数学的一部分重要内容。

 

1836年

彭赛列（Poncelet）出版了《力学在机械中的应用》（Cours de mécanique appliquée aux machines）。它第一次提出了将数学应用于机械设计。

 

1837年，泊松出版了《关于判断的概率之研究》（Recherches sur la probabilité des jugements）。在书中他确立了概率的法则，给出了“泊松大数定律”，并且对于二项分布一种限制情形的离散随机变量描述了“泊松分布”。

 

1837年

《剑桥与都柏林数学杂志》开始出版。

 

1837年

狄利克雷（Dirichlet）给出了函数的一般定义。

 

1837年

刘维尔（Liouville）讨论了积分方程，并给出了“斯图姆-刘维尔定理”用于求解此类方程。

 

1837年

旺策尔(Wantzel)证明了经典问题倍立方与三等分角不可能用尺规作图。

 

1838年

贝塞尔（Bessel）测量了天鹅座61的视差，这是第一颗被计算视差的恒星。

 

1838年，库诺特（Cournot）出版了《财富理论的数学原理之研究》（Recherches sur les principes mathématiques de la théorie des richesses），书中讨论了数学经济学，特别是供需函数。

 

1838年

德摩根（De Morgan）发明了术语“数学归纳法”，并使该方法精确化。

 

1839年

拉梅（Lamé）证明了费马大定理在n=7的情形。

 

1840年

柯西出版了四卷本《分析与数学物理习题集》（Exercises d'analyse et de physique mathematique）的第一卷。

 

1841年

高斯发表了一篇光学论文，其中给出了一个公式，用于计算给定焦距的透镜成像的位置和大小。

 

1841年

雅可比（Jacobi）撰写了《函数行列式》（De determinantibus functionalibus），致力于研究函数行列式，现在称为雅可比行列式。

 

1841年

凯特勒（Quetelet）建立了比利时中央统计局。

 

1842年

海森（Hesse）在一篇研究三次和二次曲线的论文中引入了“海森行列式”。

 

1842年，斯托克斯（Stokes）开始研究流体，出版了《关于不可压缩流体的稳定流动》（On the steady motion of incompressible fluids）。

 

1843年

哈密顿（Hamilton）发现了四元数，它是复数的四维推广。

 

1843年

刘维尔（Liouville）向法国科学院宣称他发现了伽罗华的未发表作品中的深刻结果，并承诺将伽罗华的论文以及他自己的注解发表出来。

 

1843年

库默尔（Kummer）在研究唯一分解时发明了“理想复数”。这导致了环论的发展。

 

1843年

凯莱（Cayley）在他的论文中研究了“n维几何”，他是第一个研究高维几何的人。他使用行列式作为主要工具。

 

1844年

刘维尔找到了第一个超越数，这种数不能被表示为有理系数代数方程的根。

 

1844年，格拉斯曼（Grassmann）出版了《线性外代数，数学的新分支》（Die lineale Ausdehnundslehre, ein neuer Zweig der Mathematik），其中他发展了一种代数的思想，用特定的法则来处理表示几何对象的符号，例如点、线、面等。

 

1845年

凯莱出版了《线性变换理论》（Theory of Linear Transformations），其中他研究了线性变换的复合。

 

1845年

柯西在研究置换群的时候证明了一个群论基本定理，后来被称为“柯西定理”。

 

1846年

刘维尔在《Liouville's Journal》（刘维尔杂志）发表了伽罗华的关于求解代数方程的论文。

 

1846年

14岁的麦克斯韦（Maxwell）写了他的第一篇论文《论卵形线与其他多焦点曲线》（On the description of oval curves, and those having a plurality of foci）。

 

1847年

布尔（Boole）出版了《逻辑的数学分析》（The Mathematical Analysis of Logic），其中他证明了逻辑法则可以用数学方法处理而非形而上学。布尔的工作为计算机逻辑奠定了基础。

 

1847年

德摩根（De Morgan）提出了两个集合论定律，被称为“德摩根律”。

 

1847年

斯陶特（Von Staudt）出版了《位置几何学》（Geometrie der Lage）。它第一次将射影几何从度量基础中完全解脱出来。

 

1848年

汤姆森（开尔文勋爵）提出了以他名字命名的绝对温标。

 

1849年

埃尔米特（Hermite）将柯西的留数技术应用到双周期函数。

 

关注微信：哆嗒数学网 每天获得更多数学趣文

新浪微博：http://weibo.com/duodaa