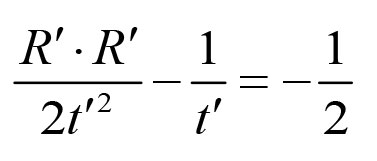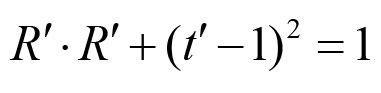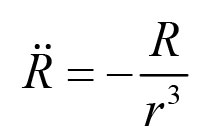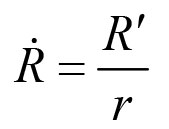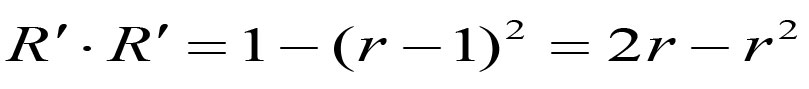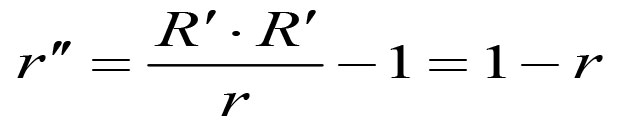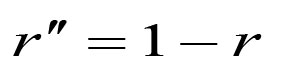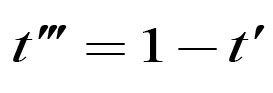微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
新浪微博:http://weibo.com/duodaa
AlphaGo和世界排名第一的中国棋手柯洁的比赛结束了。不出所料,即便柯洁这样的围棋大师,也已经完全不是我们人类发明的围棋程序的对手。但是,熟悉人工智能的人都知道,无论人工智能有多么强大,他能做出能让现在的人们多么惊奇的事情,它的本质并不是黑魔法,而仅仅是数学。
数学里有一个分支叫做博弈论,英语叫做Game Theory,直译过来就是“游戏理论”的意思。围棋是一种游戏,这个游戏的很多理论也符合博弈论的一些经典结论。博弈论里有一种游戏叫做完全信息博弈,意思是无论是自己还是你的对手,和游戏有关的所有信息都是知道的。自己能走哪里,对手能走哪里,自己之前做过什么,对手之前做过什么,都是相互知晓,没有隐藏。相反,现在最火的电脑网络游戏之一的《英雄联盟》则不是完全信息博弈,因为迷雾的影响,你在某个时刻并不知道对手是在打野还是回城升级装备。
我们的故事现在开始。

用一种数学表示围棋
诗人歌德曾经调侃:数学家就像法国人一样,无论你说什么,他们都能把它翻译成自己语言,然后完全不是你刚才说的那样。我不知道这是在膜还是在黑,我保证读完这一小节后,有很多读者都会有这样的感觉。
当执黑先行,棋盘上有19×19=361个交叉点,加上Pass(即是说不走,让对方走),黑棋有362种下法可以选择,当黑棋下完第一步,那么因为之前黑棋下过的位置不能再下,白棋还剩360个位置可以行棋。当棋局进行到某个局面,考虑到按围棋规则不能落子的点,黑棋和白棋能下位置数量会有所不同,但可选择的下法有仅仅是有限个——不超过362个。
我们把每个局面下起手可以选择下法编号,0号下法是Pass,1号下法、2号下法、……n号下法。那么不嫌麻烦,我们下棋的时候,完全可以不用摆子,叫出下法编号就可以。
比如黑棋叫出1号下法,白棋叫出8号下法,然后黑棋再叫出下完1号、8号下法局面下的5号下法,再来给白棋叫出他的下法。实际上,这个时候,黑白双方已经不是在玩一个落子的游戏,而是在玩一个叫号的游戏,叫出的都是自然数。
黑方叫号: 1 5 8 9 … 11 12
白方叫号: 8 3 6 11 … 55 4
围棋会在有限步后终止游戏,判定胜负。终止的那一刻,我们记录下了一个序列,比如上面对局的序列就是<1,8,5,3,8,…,12,4>,这是一个记录比赛进程的行棋序列,我们把这个序列一个符号x表示,特别的上面行棋序列的x(0)=1,x(1)=8,x(2)=5用它也可以来判定胜负。
按中国规则,黑棋要要还三又四分之三字给白棋。
我们制造一个集合 A = { x : x为行棋序列,x使得 黑棋子数-3.75 大于 白棋子数+3.75 }, 那么黑棋赢的表述就成了,行棋序列x∈A 。白棋赢的表述就是 x ∉ A 。
我们可以改变集合A,从而改变游戏的规则。比如比较温和的改动是改变还子个数,比如以前的围棋是不还子的。激进的改动是,如果行棋序列中使得围棋棋盘上首先出现五连珠的一方算赢,那么这游戏变成了一个可以吃子的五子棋,而不再是围棋。
但无论怎么改变集合A,有一点始终没变,游戏始终是一个完全信息的有限游戏(就是说每次能选择下法有限,游戏也会在有限步内终止)。
博弈论经典结论:完全信息的有限游戏,必有一方有必胜策略。意思是说,围棋在双方都有能力最强招的情况下,其实胜负已定。这种有一方有必胜策略的游戏,叫做决定的游戏。
穿越到未来的围棋
好吧,如果一个职业棋手对我说,“你说胜负已定,你说是黑棋赢还是白棋赢?我们来下下?”,我只能报以微笑,并认输回应,虽然最强招在数学上被证明存在,存在性并不能保证我能知道它具体是什么。就算棋力远远超过人类AlphaGo现在他也不能保证他知晓这个其实已经存在最强招法。
然而,我们可以试想一下,到某个遥远的未来。人类的智能水平发展到一个让现在的看来人匪夷所思的高度。每个人都知道围棋的最强招法,于是围棋变得无趣,因为还没有落子我们就知道了结果。
未来的人不再满足只有361个交叉点,他们设计横竖都无穷个行列(确切的讲是可数无穷),以满足每一次轮到他落子的时候,自己可以有无穷个可以落子位置。他们也不再满足在有限步结束的游戏,而把游戏规定成需要无限的进行下去。
他们还是叫号地玩游戏。这样,黑棋第一步,在0号下法,1号下法,..., n号下法,…选择出一种下法落子,然后白棋在对应局面的,0号下法,1号下法,..., n号下法,… 中选择一种应对。
棋局的出牌会变成这样:
黑方叫号: 1 3 6 81 4 …
白方叫号: 3 6 33 45 99 …
这样,行棋序列会变得无限长,成为<1,3,3,6,6,33,81,45,4,99,…>
这是一个在有限步之内无法完成的游戏。在当前的现实中,是无法完成这个游戏的。但是在数学中,无限是一个可以达到完成的实体。也许智能高度发达在未来,我们能在大脑的意念中,玩耍这个游戏。
那么如何判定输赢呢?和前面一样,事先设定一个集合A,A由一些无限长的自然数序列组成,如果最后得双方的行棋序列x是A里的元素,则黑棋赢。否则,x ∉ A 白棋赢。
新的游戏,似乎只是把有限的情况改成无限。它仍然的完全信息的游戏。那么无论我们怎么改变A,是不是黑白双方,必有赢的策略呢。
现在,我可以告诉你,之前的都是铺垫,真正的内容才刚刚开始。
这是什么游戏?
这不是小编杜撰的游戏,数学家,尤其是集合论学家们早已经研究了很多。这个游戏带来的相关论题,却和公理体系和实数结构有关系。
为了标记方便,我们把前面无限游戏下选定集合A为胜负判定集合的游戏叫做Game(A)。
为了阐述和实数的联系我们先做一个铺垫。如果你有拓扑学的基础知识的话,会很容易看懂下面再说什么。
取集合NS = { x: x为自然数的无穷序列}
对于两个自然数的无穷序列:
x = <x(0), x(1), x(2), …, x(n), …>∈NS
y = <y(0), y(1), y(2), …, y(n), …>∈NS
定义距离d( x, y) 如下:

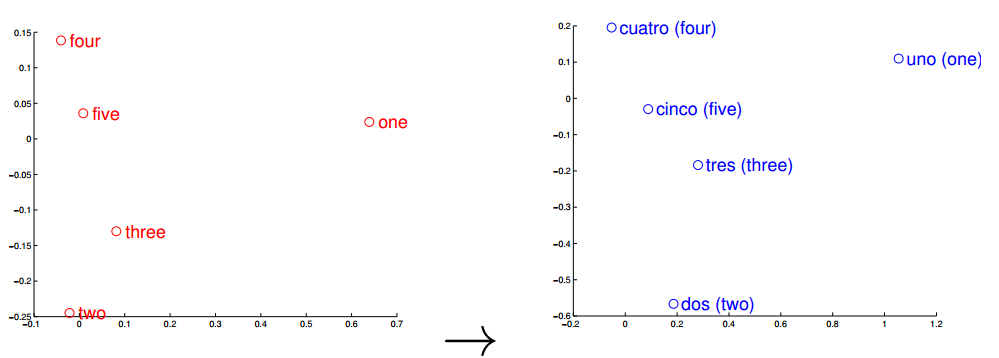
你还能验证距离函数d( x,y )在NS中还是一个完备的距离。而这个距离诱导的拓扑竟然和无理数同胚(你试试用连分数验证一下)——虽然我们知道无理数在通常的距离下,无理数并不是完备距离空间——而无理数在很多数学意义下,占有了实数的大多数。研究NS这个自然无穷序列的空间就和实数的研究联系起来了(实际上,集合论学家更关心的是Borel同构,实数和无理数是Borel同构的)。
实际上,如你可以想到的,集合论里,把一个自然数的无穷序列称为实数。实际上,集合论学家把他看成实数的一种形态。下面的部分,当我们说到实数的时候将不区分这样的具体形态。
是不是我们无论怎样改变集合A, Game(A)的黑棋和白棋中都有一方有必胜的策略呢?
在现行使用最多,也最被人接受的数学公理体系ZFC中,你是可以用选择公理构造一个集合,使得黑白双方都没有必胜策略。
有很多办法,从不同角度去构造这样的集合。但我们不会在这里去表述这种集合的构造细节。这里只是提示一下其中的一个办法:无论黑棋的策略或者白棋的策略,都只有连续统基数c那么多个,而实数的子集实在是比这个多得多。用这个实数,超限的归纳和用一些对角线方法,就能造出这样的集合。
有一个集合A,使得游戏Game(A)的对局双方都没有必胜策略。但是,只要有人愿意开一把,行棋的序列总能判定胜负——这样的游戏是不是变得好玩了呢。
一些人的吐槽:选择公理是真的吗?
“什么?居然有一个集合A,让Game(A)不能被确定,我完全不能接受!”好吧,熟悉选择公理的人一定会说,选择公理做出来的东西不具有构造性,那意味着样的集合是看不清也摸不着的。的确,有的人更愿意相信所有的Game(A)应该有一方有必胜的策略,有就是说,游戏是决定的,这就是决定性公理。
决定性公理(Axiom of Determinacy,简称AD):对所有NS中的子集,所有的Game(A)都是决定的。
按照一般的要求,一个命题要成为公理,它应该至少要和常用的策梅洛-弗兰克尔公理体系(ZF公理体系)不矛盾,集合论中叫做协调。但是,这里有个很奇怪的结论,因为AD能推出ZF体系是协调的,于是根据哥德尔的第二不完备定理,ZF + AD这个体系是否相对于ZF协调,不能被证明。
另外,虽然ZF+AD中对普遍的选择公理(即任意多的集合簇有选择函数)不成立了,但是它对选择公理的的否定没有完全彻底,对可数选择公理还是成立的——ZF+AD能将可数个集合有选择函数变成定理(Countable Choice)。
于是,实分析中一些常用的定理,在ZF+AD还是成立的(至少在实数范围内是成立的),比如
可数个可数实数子集的并还是可数的。
海涅归结原理:当x→a时,实函数f(x)→b,当且仅当,对任意序列x(n)→a,n→∞,f(x(n))→b。
贝尔纲定理:实数这个完备度量空间中,可数个稠密开集的交稠密。
历史上,波莱尔曾经旗帜鲜明地反对选择公理,但他认为可数的选择公理是可以的,并且可数选择公理就够了。也许决定性公理可以成为他的一个选项。
实际上,决定性公理会牵涉到实数的一些底层性质。而这些联系,是通过设计一些新的游戏来展示的。
新游戏一:关于第一纲集和贝尔性质
如果一个集合的闭包没有内点,那么这样的集合被称为无处稠密集合。而第一纲集就是可数个无处稠密集合的并。
一个集合如果它和某个波莱尔集的对称差是第一纲集,我们说具有贝尔性质。
我们现在来看一个新的游戏。在之前的Game(A)中,黑白双方叫出的是一个数字,而这个新游戏中,黑白双方叫出是一串数字,一个有限长度的自然数序列。
黑方叫号: <0,3,5,6> <2,1> <8, 9,7,9,5,9> <4,12,5,7,8,0> ...
白方叫号: <0,5> <2,1,34,5> <9> <4,12,5,7,8,0> ...
同样,我们把这些序列拼接起来,能得到一个无限长的自然数列,比如上面的拼接起来就是 <0,3,5,6,0,5,2,1,2,134,5,8, 9,7,9,5,9,9,4,12,5,7,8,0,4,12,5,7,8,0, ...>
我们还是设定一个集合A,规定得到的序列x∈A,黑方赢,否定白方赢。
这个游戏叫做Banach-Mazur游戏,在设定的集合A下,我们把它名字叫做Game1(A)。
如果你理解了前面的编号思想,你很容易想清楚,如果所有的Game(A)是决定的,那么所有的Game1(A)也是决定的。
你可以试试证明这样一个事情:Game1(A)中,白方有必胜策略,当且仅当,A是第一纲集。
于是,有人能利用上面的结果,得到:
如果决定性公理成立,则任何实数子集都具有贝尔性质。
因为,贝尔性质是一种拓扑性质,所有决定性公理其实能说明实数在拓扑性质上的一些确定性。
新游戏二: 完备集性质和连续统假设
如果一个实数子集是没有孤立点的闭集,我们说这个集合是完备集。如果一个实数子集是有限的或可数,再或包含一个完备集,那么我们说这个集合具有完备集性质。
我们新游戏二的规则发生重大改变。黑方能叫的号还是一串数字,不过数字只能在0和1中选择,而白方只能叫出一个数字,同样只能在0,1中选择。
黑方叫号: <0,1,1,0> <0,1> <0, 1,1,1,1,1> <0,0,1,1,0,0> ...
白方叫号: 0 0 1 0 ...
同样,我们把这些序列拼接起来,能得到一个无限长的0-1列,比如上面的拼接起来就是,<0,1,1,0,0,0,1,0,0, 1,1,1,1,1,1,0,0,1,1,0,0,0,...>。
这里,我们其实已经只是在0-1序列组成的空间里叫号了。
取集合TS = { x: x为0-1无穷序列},
x = <x(0), x(1), x(2), …, x(n), …>∈TS
y = <y(0), y(1), y(2), …, y(n), …>∈TS
这个TS空间里,如果我们按前面相同的方式定义距离

那么通过这个距离诱导得到的拓扑空间,和康托集同胚。
我们设定一个TS的子集A,规定得到的序列x∈A,黑方赢,否定白方赢。定名Game2(A)。
同样,用一些小技巧,我们可以知道,在决定性公理成立的情况下,所有的Game2(A)都是决定的。
关于这个游戏,有两个经典的结论。
Game2(A)中,白方有必胜策略,当且 仅当,A是可数或者有限集合。
Game2(A)中,黑方有必胜策略,当且仅当,A是包含一个完备集合。
于是,如果决定性公理成立,那么任何实数子集都有完备集性质。
如果,你对完备集合一些性质比较熟悉的话,会知道完备集合的是和实数集合等势的。于是,我们在决定性公理成立的情况下,得到一个比较弱的连续统假设成立:任何一个实数子集要么和实数等势,要么至多可数的势。
新游戏三:勒贝格测度与可测集合
这里,由于篇幅原因,我们不再具体介绍新游戏三了。新游戏三的大致思路就是,想办法把游戏移植到传统形态的实数上去,并把勒贝格测度结合起来。通过前面两个变种游戏,大家应该能相信,这样事情是能办到的了吧。
这里要说的重点是下面这个有意思结论。
如果决定性公理成立,所以实数子集都是勒贝格可测的。于是什么不可测的Vatali集,Banach分球怪论什么的,都不存在了。
结束
我们从一个传统的围棋游戏开始讲述,把围棋用数学转化成了一个大家只呼喊自然数的游戏,然后进一步让它“进化”成了一个无穷游戏。然后发现它居然能与实数的结构有着深刻的联系,难怪有集合论学家自嘲:
集合论学家就是一群不知道实数是什么的数学家。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
新浪微博:http://weibo.com/duodaa






























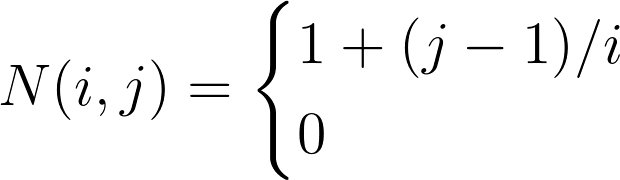

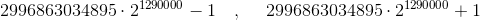

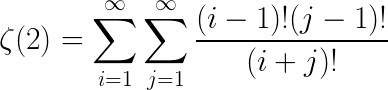


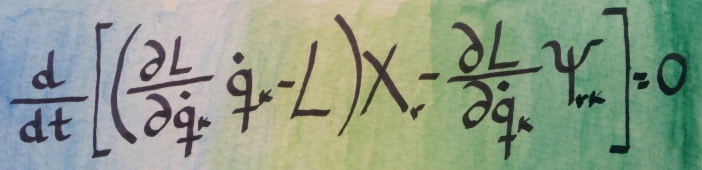


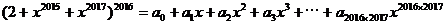 ,那么
,那么 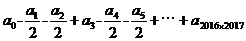 的值是多少?
的值是多少?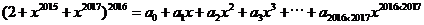 ,所以常数项容易求,在等式两边令x=0,则有a_0 = 2^2016。但是右边会出现一次项二次项吗?笔者感觉x的最小指数应该是2015,貌似a_1, a_2, ……, a_2014应该为0。
,所以常数项容易求,在等式两边令x=0,则有a_0 = 2^2016。但是右边会出现一次项二次项吗?笔者感觉x的最小指数应该是2015,貌似a_1, a_2, ……, a_2014应该为0。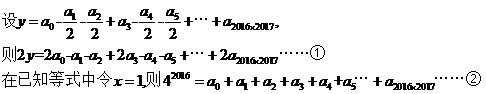
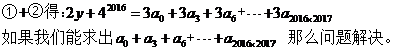
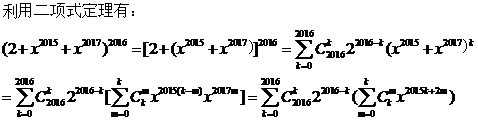
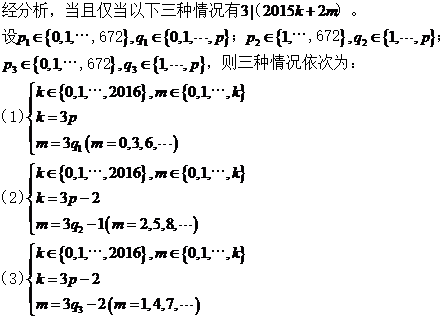
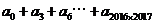 ,所以
,所以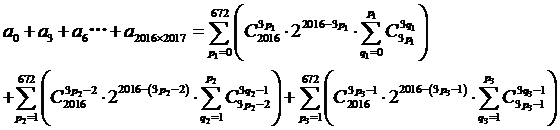
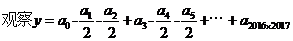 ,三个一组三个一组,每组中连续出现两个-1/2 ,太奇怪了。由【疑问一】、【疑问二】可知,用常规的实数0,1赋值不可能有这种效果出现。想想我们所见过的成千上万不计其数的数,实数也好虚数也罢,哪一个数的整数次幂会以3为周期,并且同时含有系数 ?
,三个一组三个一组,每组中连续出现两个-1/2 ,太奇怪了。由【疑问一】、【疑问二】可知,用常规的实数0,1赋值不可能有这种效果出现。想想我们所见过的成千上万不计其数的数,实数也好虚数也罢,哪一个数的整数次幂会以3为周期,并且同时含有系数 ?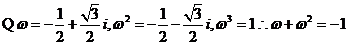
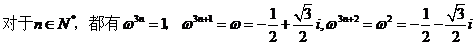
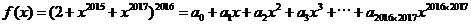
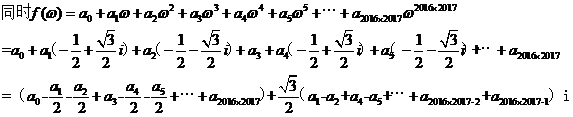
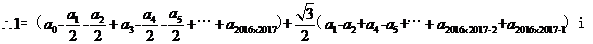
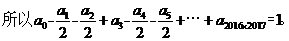
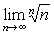 这一个极限上摸不着头脑:这是一个的“∞的0次方”形式的未定式,因此常规的四则运算都对其无济于事。
这一个极限上摸不着头脑:这是一个的“∞的0次方”形式的未定式,因此常规的四则运算都对其无济于事。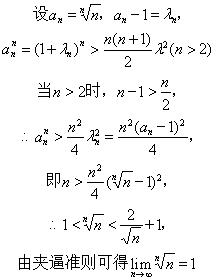
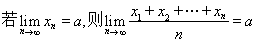

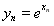 ,则可以得到以下结论:
,则可以得到以下结论: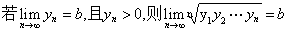
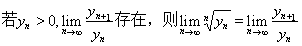
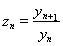 ,则又可以得到以下结论:
,则又可以得到以下结论: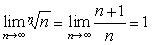
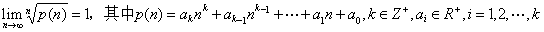
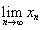 与
与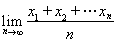 均存在的情况下,引理1及其逆命题是互相等价的。因此我们并不需要用上stolz这把“牛刀”去宰一只鸡,而仅仅使用其一个特殊情况就够了。
均存在的情况下,引理1及其逆命题是互相等价的。因此我们并不需要用上stolz这把“牛刀”去宰一只鸡,而仅仅使用其一个特殊情况就够了。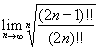 ,其中
,其中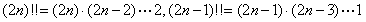 ,
,
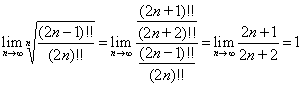



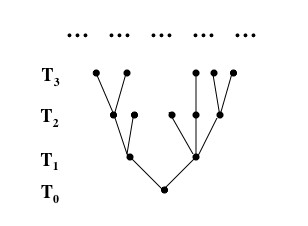









































 ,
,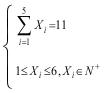
















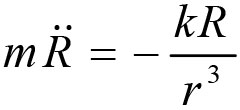
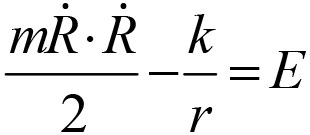
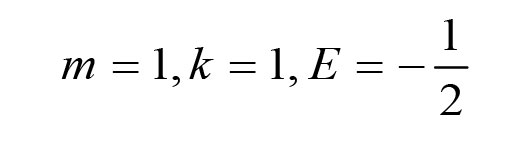
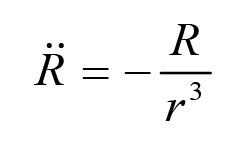
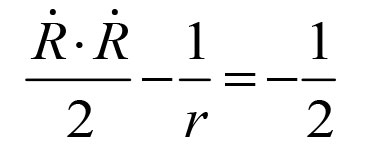
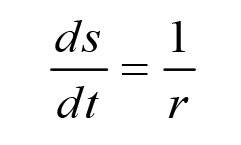
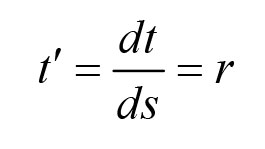
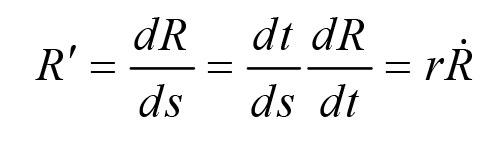
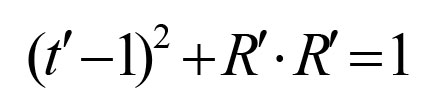
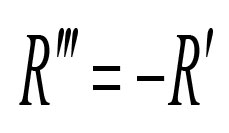
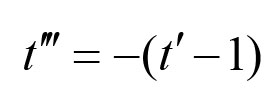
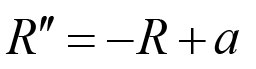
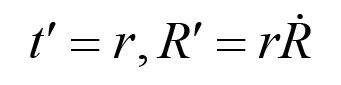
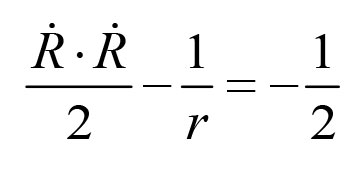
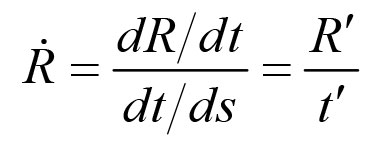
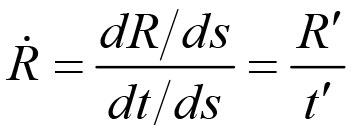 )
)