从深圳某公园的错误谈起:你看到的数学可能是不对的!
作者:欧阳顺湘,本文转自其公众号和乐数学(kelemath)
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa





















关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

作者:欧阳顺湘,本文转自其公众号和乐数学(kelemath)
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa






















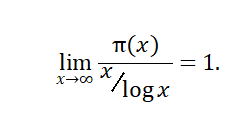

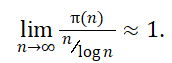
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
一位杰出的数学家运用物理学中的概念研究了困惑人们数千年的数学问题,并取得了进展。
数学里面充满了超自然的数的系统,其中大部分人从来没有听说过,甚至理解起来有困难。但是有理数是家喻户晓的,它们是自然数和分数——这些有理数你从小学就知道了。但是对于数学家来说,最简单的问题往往最难理解。它们简单的就像一堵抗风墙,没有裂缝、突出物或者明显你可以抓住的某些东西。
牛津大学的一位叫金明迥的数学家,对于寻找哪些有理数可以解特定类型的方程特别感兴趣。几千年来无数数论学家挑战过这个问题。他们在解决问题方面进展甚微。当一个问题研究了很久却没答案,我们很自然的就认为唯一的出路就是有一个人能提出新的想法。这个人就是金明迥。

“即使我们已经研究了3000年,但研究这些问题依然没有太多的技术手段。所以任何人无论何时提出一个可靠的新方法去解决它都是一个大的进展,这就是金明迥所做的。”威斯康星大学的数学家乔丹·艾伦伯格(Jordan Ellenberg)评论道。
在过去的十年间,金明迥想出了一个非常新颖的方法----在看似无规律的有理数域寻找模式。他将这种方法写进论文里,发布在讨论会中,并将其传递给学生,现在学生们自己继续进行研究。但是他一直保留着一些东西, 他的思想正走向成熟,不是基于纯粹的数论,而是从物理中借用概念。对于金明迥来说,有理数解多少有点像光的轨迹。
如果这样的联系让你觉得像天方夜谭,那就对了,因为一些数学家也甚至和你有相同想法。由于这个原因,金炯明长期以来没有吐露这个想法。“我将它藏了起来,因为一直以来我多少会因为物理联系而不安,”他说。“数论学者是一群相当严谨刻板的人,物理的因素的加入有时使他们更加怀疑我做的数学。”
但是现在金明迥说他已经打算向世人表达他的想法。“我想这个改变单纯的是因为思想成熟起来了!”53岁的金明迥在我们交流这个故事的一封邮件的开头写到。
他最近已经举办了一场学术会议,邀请了数论学家和弦论学家。他也为还没有习惯于通过直接类比物理世界来思考数论问题的数学界写一篇文章去描述他的想法。
至今仍有一个绊脚石——数学和物理类比的最后一部分,金明迥仍需要继续攻克下去。他希望邀请更多的人去参与他的研究,特别是物理学家,他需要物理学家的帮助去完善它。
一个古老的挑战
方程的有理解深深地吸引着人们。找到方程的有理解,就像拼图块完美地落实到对应的位置那样令人满足。基于这样的理由,数学中很多著名的猜想都是关于方程有理解的。
有理数包含整数和任何可以表示为两个互素的整数之比的数。例如1,-4以及99/100.数学家对丢番图方程(Diophantine equation)——整系数多项式方程的有理数解特别感兴趣。就像x²+y²=1。公元3世纪,生活在古希腊亚历山大城的丢番图就研究了很多这样的方程。
有理解很难用全面的方法所找到,因为他们不遵循任何几何模式。考虑方程x²+y²=1。它的实数解是一个圆,拿走在这个圆上的所有不能表示为分数的点,所留下的就是有理解,而这样的解不会形成一个规则的形状。有理解是随机分布在圆周上的。
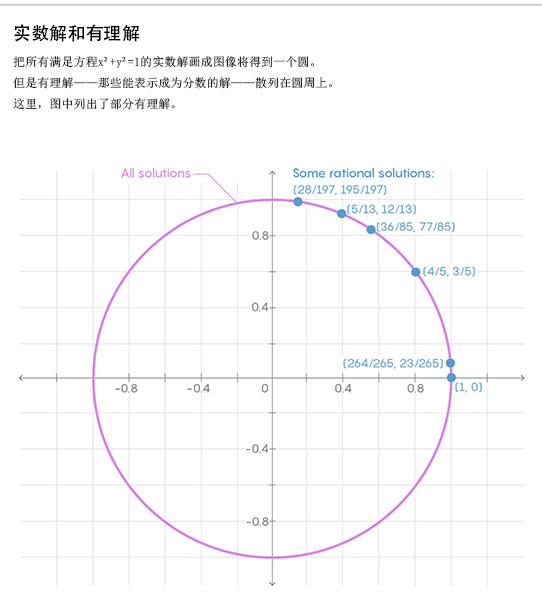
“具有有理坐标点的条件根本不是几何条件。 你无法知道如果一些有理点满足某方程,它必须满足写什么条件”金明迥说。
有的方程,通常容易找到某个单一的有理解,甚至许多有理解。但对于不喜欢松散结果的数学家来说,他们对研究所有的有理解更有兴趣。这样问题就会难很多了。事实上,甚至是关于有理数最直白的结果,足以让你在数学圈出人头地。如同在1986年,一个名叫法尔廷斯(Gerd Faltings)的数学家荣获了数学最高荣誉的菲尔兹奖,他就是解决了一个叫莫德尔猜想(Mordell conjecture))的问题,证明了一族特定的丢番图方程仅有有限多的有理解(而不是无限多解)。
法尔廷斯的证明在数论中是一个具有举足轻重的结果。但这也是数学家所说的“无用的证明”,事实上这意味着它没有精确计算出有理解的数量,更不用说找出它们了。从那以后,数学家开始寻找解决下一步的方法。有理点看起来就像一个方程的普通图像上的随机点。如果他们改变他们所研究问题的条件,数学家们希望这些点将看起来像一个星座一样,他们能以一些精确的方式去描述。但问题是,在已知的数学领域并没有给出这样的条件。
“为了得到关于有理解的有效结果,人们当然会认为,解决这个问题需要一个全新的想法。”艾伦伯格说。
目前,关于新想法是什么样,有两个主要研究。一个来自于日本数学家望月新一,2012年,他在京都大学的教职员网页上发表了数百页复杂又新奇的数学成果。五年后,他的论文依然是高深莫测的。而另一个新想法就来自于金明迥。他试图在扩张的数论空间中思考有理数,在这其中隐藏的模式开始出现。
一个对称解
数学家通常说研究对象的对称性越好,就越容易研究。鉴于此,他们希望将丢番图方程的研究置于比问题本身产生的空间更对称空间中。如果他们能这样做,他们可以利用新的相关对称性去追踪他们所寻找的有理点。
为了见识一下对称性如何帮助数学家解决问题,画一个圆。可能你的目标是定义在圆上的所有点。对称性是一个有用的工具因为它创建了一个映射,可以让你从已知点的性质推出未知点的性质。
想象一下,你已经在下半圆找到了所有的有理点。因为圆是反射对称的,你可以水平直径为对称轴翻转下半圆的有理点(改变所有y坐标的符号),于是一下子你就可以得到在上半圆的所有有理点。事实上,一个圆拥有丰富的对称性,即使知道一个单点的位置,结合对称知识,如果你需要找圆上的所有有理点,只要围绕原点无限旋转对称就可以得到。
但是如果你处理的几何对象有着高度无规律性,就像一个随机游走路径,你将需要努力去分别独立找出每一个点——这儿没有对称关系帮助你去将已知点映射到未知点。
数的集合也可以拥有对称性。集合的对称性越多,就越容易去理解——你可以应用对称性去发现未知的值。具有特定类型对称关系的数聚在一起形成一个“群”,数学家可以使用群的性质去理解包含在其中的所有的数。
一个方程的有理解集合不具有任何对称性也不形成一个群。从而使数学家们不可能一次性就发现所有的解。
从二十世纪40年代开始,数学家们开始探索一种方法去将丢番图方程的解放到一个拥有更多对称性的空间中去找。数学家沙博蒂(Claude Chabauty)发现在他构建的更大的几何空间的内部(通过一个被称为p进数(p- adic numbers)的扩张的全域),有理数形成了自己的对称子空间。他开始用这样的子空间与丢番图方程的图像联系起来。两个空间相交的点就是方程的有理解。
在二十世纪80年代,数学家科尔曼(Robert Coleman)对 沙博蒂的结果进行了改进。 在那之后的几十年里,科尔曼-沙博蒂方法成为数学家寻找丢番图方程有理解最有效的工具。但只有当方程的图像与更大的空间大小成比例时,它才起作用。当不成比例时,那么就很难精确找出方程曲线与有理数相交的点。
“如果你有一条曲线在空间内,而且有太多有理点,这些有理点集纠结在一起,你就很难区分哪些有理点在曲线上。”一位在加州大学圣地亚哥分校名叫凯德拉亚(Kiran Kedlaya)的数学家说。
于是,金明迥开始着手起这个问题了。为了在沙博蒂的基础上取得更进一步的成果,他希望去寻找一个甚至更大的空间去思考丢番图方程——一个有更多有理点分布的空间,于是他就可以研究更多不同种类丢番图方程的相交点。
空间的空间
如果你在寻找一个更大的空间,以及在思考如何沿着对称这条线索来寻找答案,借助于物理办法是个好的选择。
一般来说,在数学的意义上,一个空间是一个拥有几何或拓扑结构的点集。随意分散的一千个点不会形成空间,因为没有任何结构将他们联系在一起。但是对于一个球,由特殊的连续分布的点构成,它是一个空间。同样的环面、二维平面、或者我们生活中四维时空也是一个空间。
除了这些空间外,存在更多的风格迥异的空间,你可以把它看成“空间的空间”。举一个非常简单的例子,想象你有一个三角形——这是一个空间,那么继续想象所有可能的三角形,它们组成一个空间。在这个更大空间内的每一点代表一个特定的三角形,由它所表示的三角形的角的顶点的坐标。
这样的想法在物理中非常有用。在广义相对论的框架下,时间和空间不断演变,物理学家把每个时空看作是所有时空所组成的空间中的一个点。空间的空间在规范场论这个物理领域中出现过,这与物理学家在物理空间之上建立的场有关。这些场描述了你在空间中运动时,这些力如何起作用,如同你看到的电磁力和重力一样。你可以想象,在空间的每一个点上,这些场的构造都略有不同——而且所有这些不同的构造聚在一起形成了更高维度的“所有场的空间”中的点。
这个物理学中场的空间与金明迥在数论中提出的观点类似。为了便于理解,我们考虑一束光。物理学家想象光穿过高维的场空间。在这个空间中,光线将遵循“最小作用量原理”的路径——也就是从A到B所需最短时间的路径。这个原理解释了为什么当光从一个介质到另一种介质会弯曲——弯曲的路径花费的时间最少。
物理学中出现的这些更大的空间的空间具有额外的对称性,这些对称性并不存在于它们所代表的任何空间中。通过对称性可以找出特殊点,例如强调的时间最短路径。在另一种情况下以另一种方式构建,这些相同类型的对称可能会注重其他类型的点——如对应于方程的有理解的点。
理学中出现的这些更大的空间空间具有额外的对称性,这些对称性并不存在
对称性与物理之间的纠缠
数论没有粒子可以追踪,但是数论多少有点像时空,为此它也提供了一种寻找所有可能的路径方法和构建对所有可能路径的空间。从这种基本的对应中,金明迥提出了一种方案:寻找光的轨道以及探寻丢番图方程的有理解是同一个问题的两个方面.正如他在德国海德堡举行的数学物理会议上解释的那样。
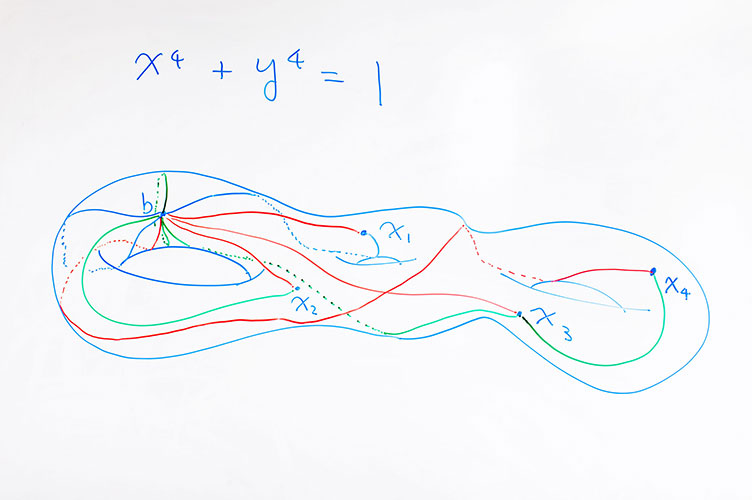
丢番图方程的解形成空间是由方程定义的曲线。这些曲线可以像圆一样是一维的(一维流形),或者他们可以是更高维的空间。例如,如果你试图寻找丢番图方程———x^4+y^4=1的复解,你就得到了一个三孔环面。在这个环面上的有理解缺乏几何结构,这样就很难去找到他们,但是它们可以被做成对应于具有结构的空间的更高维空间中的点。
金明迥通过考虑可以在环面上绘制环的方式(或等式定义的任何空间)来构造空间的高维空间。绘制环的过程如下:首先,选择一个基点,然后从该点绘制一个环到任何其他点,然后再返回。重复这个过程,画出连接基点和圆环面上其他点的路径。最后,你会有一个所有可能的环,他的起始点和结束点都在基点。这种环的集合是数学中一个重要的中心对象,它被称为空间的基本群。
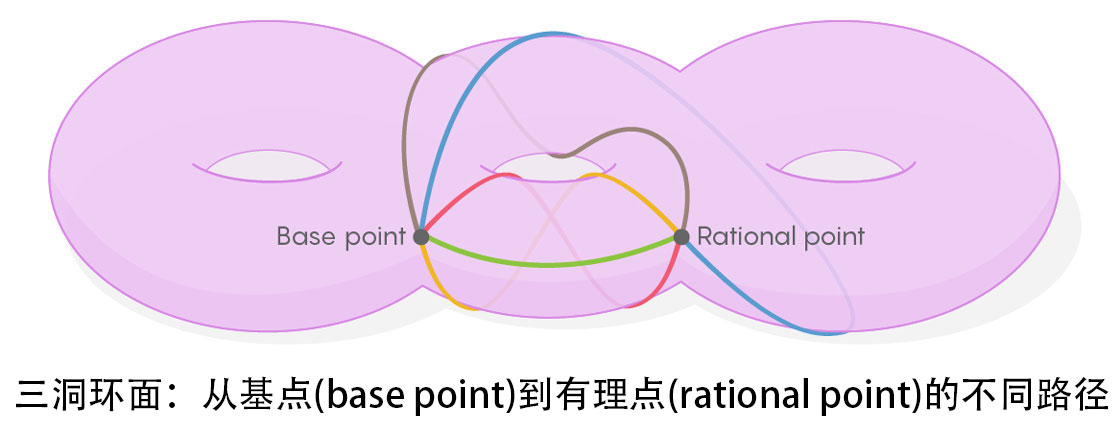
你可以使用在环面上的任何点作为你的基点。每一个点将有一个独一无二错综复杂的路径。每一个这些路径的集合可以被表示为一个点在一个更高维的“路径集合的空间”(就像所有的可能的三角形的空间)。这个空间的几何上非常类似于物理学家在规范场理论中构造的“空间空间”。当从一个点移动到环面上另一个点时,路径集合的变化非常类似于在实际空间中从一个点移动到另一个点时场变化的方式。
空间的空间具有额外的对称性,不表现于环面本身。虽然环面上的有理点之间没有对称性,但如果你进入所有路径集合的空间,就可以找到与有理点相关的点之间的对称性。这样你可以得到之前所看不见的对称性。
“我时常用到的一个短语是这些路径中有一种“隐藏的算术对称性”,高度类似于规范场论中内在的对称性”金明迥说。

就像沙博蒂所说的那样,金明迥通过考虑在他所构造的更大的空间结构中交叉的点去寻找有理解,同时运用这个空间中的对称性去限制空间中的交叉点。他希望建立一个方程去精确的找到这些点。
在物理环境中,你可以想象光线可能会采取的所有可能的路径。这是你“所有路径的空间”。在这样的空间中,引起物理学家兴趣的是与时间最小化路径相对应的点。金明迥认为寻找有理点的过程与错综复杂的路径对应的点具有同样的性质——也就是说,当你开始思考丢番图方程的几何形式时,这些点将最小化某些性质。只是他还没有找出这种性质是什么。
“我开始寻找的东西是一个在数学环境中的最小作用量原理,他在邮件中写道。“我还是不太清楚,但我有信心,它就在那里,我能找到它。”
一个不确定的未来
在过去的几个月 ,我对几位数学家描述了金明迥由物理所启发的想法,他们都仰慕金明迥对数论的贡献。然而,当把金明迥遇到的困难传达给他们时,他们并不知道该如何下手。
“作为一个具有代表性的数论学家,如果你向我展示了金明迥一直在做的所有的这些“恐怖”的事情,并问我是否受到灵感启发,我会说'你到底在说什么鬼话?'”艾伦伯格如是说。
至今,金明迥并没有在他的论文中提及物理学。取而代之的是,他把他的目标称为Selmer簇,他考虑Selmer簇在所有Selmer簇空间中的关系。这些对于数论学者来说是可识别的术语。但是对于金明迥来说他们一直是物理学中某些物体的另一个名称。
“利用物理学中的思想去解决数论中的问题是有可能的,但是我还没有想好如何建立起这样的框架,”金明迥说,“我们在一个关键点上,对物理的理解足够成熟,以及有足够多的数论学者对这个问题感兴趣,所以接下来我们需要进一步推进。”
阻碍推进金明迥的方法一个困难在于在所有错综复杂的圈所组成的空间中寻找一些最小作用量的类型。在物理世界中,这样的观念十分自然,但是在算术中并不那么显然。甚至是对金明迥的工作了解最深的数学家,也非常关心他是否会找到它。
“我认为金明迥的工作将会给我们带来许多有价值的东西。我不认为我们要像金明迥想要的那样清晰的理解有理解所在的地方是某种算术规范场理论(arithmetic gauge theory)的经典解”哈佛大学数学物理教授阿尔纳夫·特里帕蒂说。
今天,物理学的语言几乎完全在数论的实践之外。金明迥认为这种情况肯定会改变。40年以前,物理和几何、拓扑的研究几乎都是独立。但在20世纪80年代,屈指可数的几位数学家和物理学家建立了有效的方法,该方法运用物理去研究形状的性质,现在这些学者都是领军人物了,而且该领域从未停止向前。
“如今不了解物理学几乎不可能对几何学和拓扑学感兴趣。我有理由确信在数论上也会有这种情况发生”在接下来的15年,金明迥说,“这样的联系将变得十分自然。”
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,David Austin,大峡谷州立大学。
翻译作者,小涟猫,哆嗒数学网翻译组成员。
校对,333。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
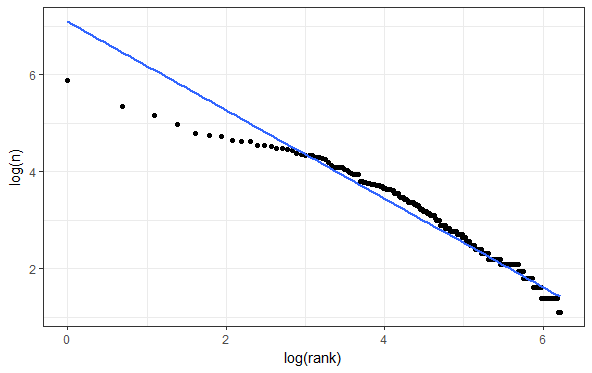
下面这张图片以矩阵形式包含了3871488个像素。每个像素的颜色由红绿蓝分量决定,每种颜色占一字节内存,我们可能想当然地认为,这个图片会占11614464字节内存,但是这个JPEG 文件实际只占734268字节内存,约为原来十六分之一。下面我们将会介绍这种由联合图像专家小组(JPEG)开发的高效图像压缩算法。

相比专门使用红绿蓝三种颜色分量,用另外三种不同的分量来描述会更方便:亮度Y, 与颜色明亮程度密切相关;C_b、C_r为蓝色、红色色度分量,它们可以粗略地确定一个色彩。上述两种表示方法可以通过一个可逆的仿射变换实现相互转换。例如,为重新获得红、绿、蓝分量的值,我们可以用以下公式:

可以看出,亮度与三种基本颜色分量的作用相同。为了可视化这个变换,我们保持亮度不变并且混合各类色度值得到以下颜色
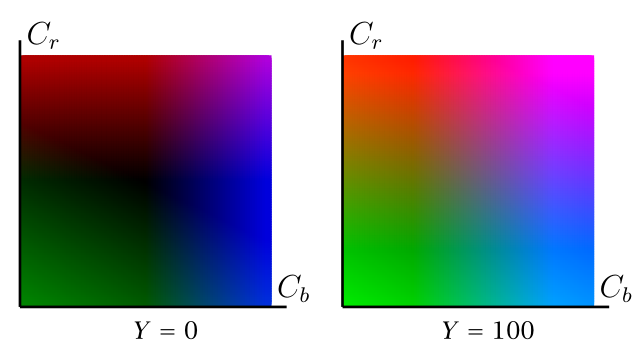
这个算法将图片分割为8*8的可单独处理的图像块,这是一个样本模块。

在我们的样本模块中,(Y,C_b,C_r)三种分量的分布情况如下,明亮的区域对应更大的数值。

可以看出亮度值Y产生的是原图的灰度图。心理可视化实验表明,人眼对亮度变化最为敏感,因此对颜色转换时可以把最重要的信息压缩到单个分量中。彩电使用相似的颜色模型,它能让黑白电视也可以有效播放貌似彩色效果的图像。
原因稍后解释,现在我们用一些频率越来越块的余弦函数的线性组合求表示各个分量值。例如,如果Y_ x,y 代表图像块中的第x 行,第y 列的方块处的亮度,就可以表示为
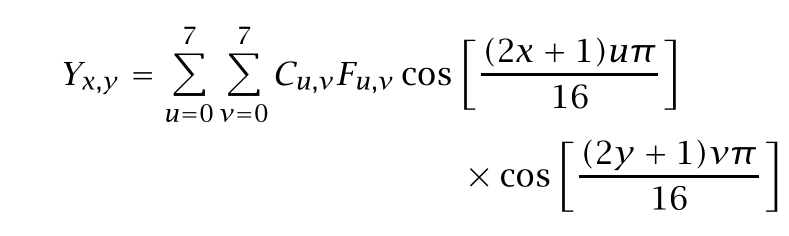
归一化常数C_u,v 不需过分关注; 系数F_u,v由二维离散余弦变换(DCT)得到,而对于它的高效计算则可以采用快速傅立叶变换(FFT)。
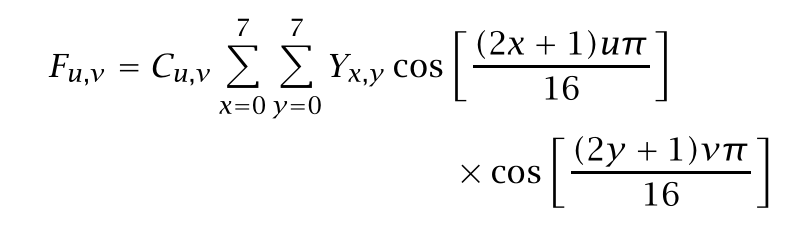
大多数图像块的分量值不会急剧改变,人眼对这些变化也不是很敏感,因此,频率较高的DCT 变换系数可能很小甚至忽略也不影响对我们对于图像的感知。这样的观察启迪了我们,也许可以以整数的形式来量化DCT的系数并加以存储。
量化过程涉及两个要素。第一个为参数α,它由使用者选择,用于控制压缩程度与图片质量。α值越大,文件越小,图片质量也就越差。
第二个因素是一个8*8的矩阵Q=[Q_u,v],其中的系数为对F_u,v /αQ_u,v取整后的值, 依经验选取Qu,v时,为了弱化高频的影响,通常对于高频部分赋予较大的数值。例如,一个用于量化亮度离DCT系数的矩阵为
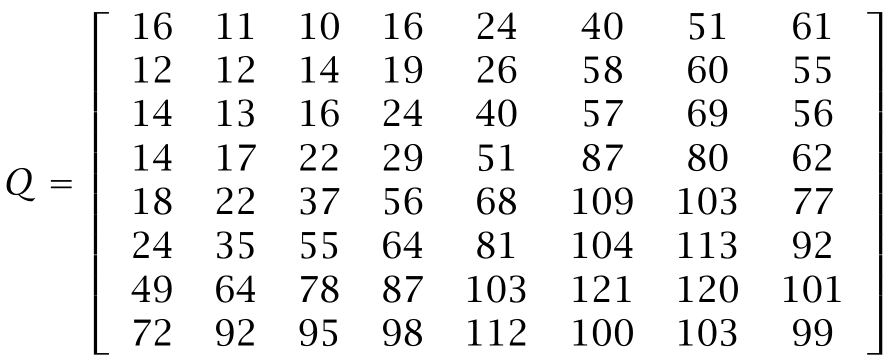
考虑到亮度携带更多重要的视觉信息,所以我们用不同的矩阵来分别量化描述亮度的系数与描述色调的系数。用中间值α处理我们的样本图像块,量化后的亮度系数如下
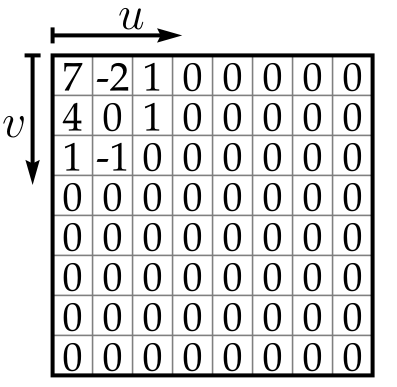
量化后的系数按照箭头指向排序,低频排在前面。
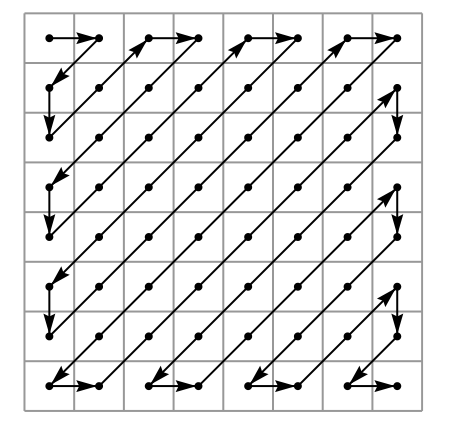
样本的亮度分量,其量化后的系数为数列 7, -2, 4, 1, 0, 1, 0, 1, -1以及55个0。相比存储这么多数字零,我们直接记录零的个数,这样极大减少了存储需求。后续的压缩要依靠哈夫曼编码来实现系数数列的高效效存储。
图像的重建可以通过逆过程实现。量化系数给出了F_u,v的近似值,这些反过来又给出了Y, C_b , C_r和R,G,B 分量的值。下图中左图表示原图,右边则是重建后的图。
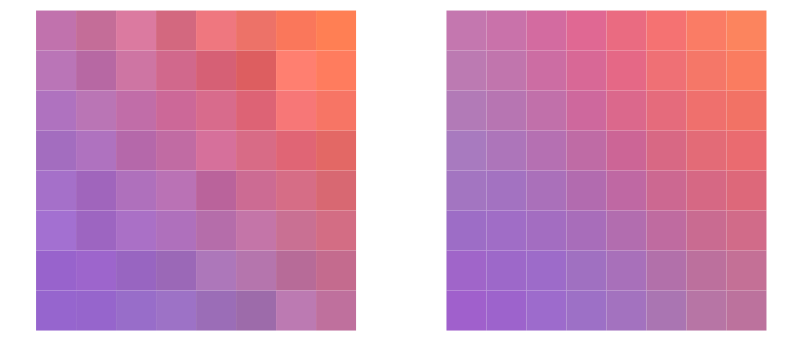
DFT似乎比DCT 更好用,因为它易于计算。但是我们却选择了DCT,这是因为我们希望把信息尽量集中到频率较低的系数上。以8*8模块中的某一行Y_x的值为例, DFT方法将Y_x表示为一些周期为8的函数的线性组合,并由此给出了Y_x的一个周期延拓。但该变换非常不必要地将 y_7 与 y_8 = y_0之间的变化也记录下来了,这就导致了高频分量的加入以及由此产生的显著影响。在下面的图中,Y_x 值用黑色表示,而由傅立叶变换的三个最低频项所给出的近似值是用红色表示的。
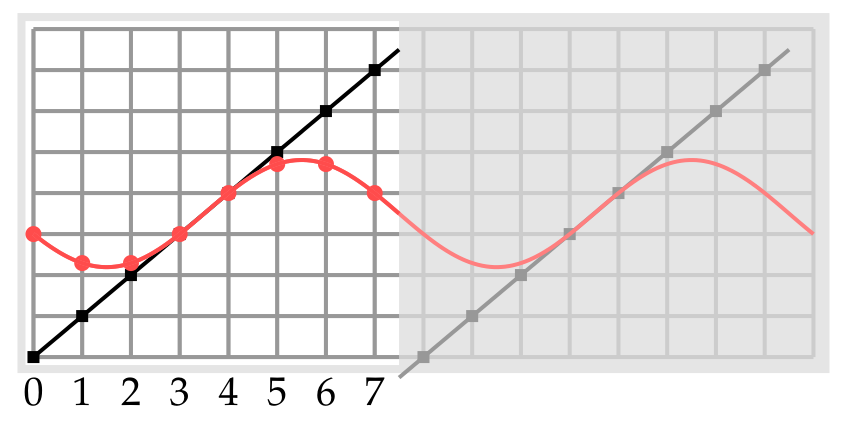
与之相比,DCT方法将Yx表示为一些周期为16且关于x=7.5对称的函数的线性组合。这使得Y_x的近似延拓更为平滑,从而减少了对高频分量的依赖。下图是DCT所给出的近似值,注意到近似效果得到了显著改善。
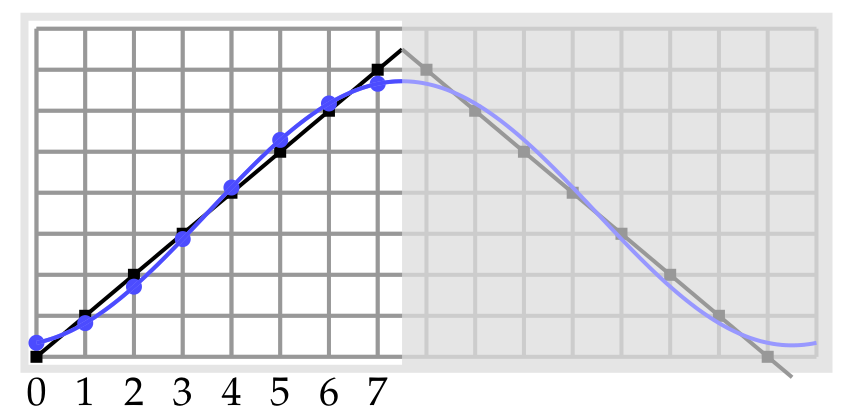
因为这些8*8图像块都是被独立处理,所以这就导致了在高压缩率的情况下边缘部分的不连续性变得十分明显。除此之外,我们通常还希望用中等分辨率就能高效重建图像。这些因素以及一些其他原因,促使了JPEG2000压缩算法的产生。在诸多不同点中,JPEG2000还采用离散小波变换代替了DCT
JPEG2000算法把图像分割为尺寸更加精细的图像块,比如256*256。为了演示小波变换,取图像块中的一行像素并令y_x 代表该行中的某一个值。现在求小波系数。
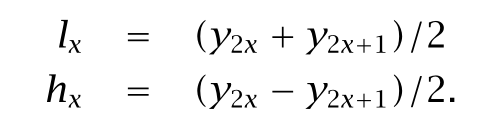
h_x为能够检测到高频变化的高通系数,l_x为低通系数。按照低通系数在前高通系数在后的顺序进行排序,对列也做相同处理后,可得小波系数的数表。
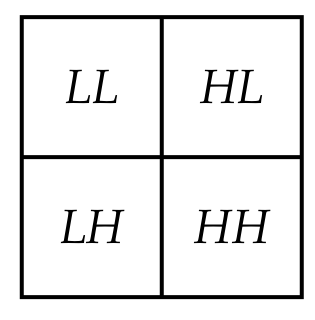
位于LL子块中的系数是通过对所有2*2的邻近像素点取平均值得到的因此代表了一个低分辨率的图像。另外三个子块描述了当重建高分辨率图像时所必要的变换。我们对LL子块重复之前的处理,从而实现以越来越低的分辨率存储图像。
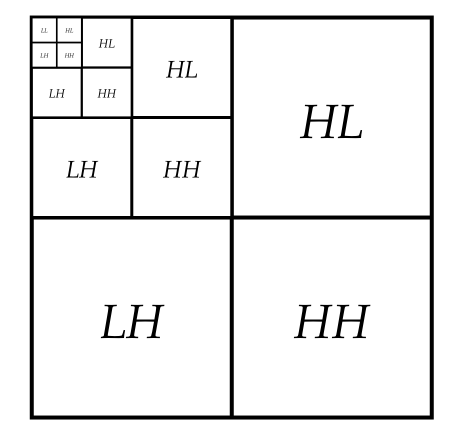
量化的过程会检测数值变化不明显的区域,从而可以安全地忽略高通系数。和之前介绍的小波变换求取两个相邻值的平均值不同的是,JPEG2000算法使用Cohen-Daubechies Feauveau (9, 7) 小波变换,它可实现取邻近九个值的平均值,这样可令图像更加平滑。
JPEG2000的算法复杂度比JPEG高一个数量级,而且在中、低压缩率时,图像质量并没有优化多少。但是在高压缩率情况下,JPEG算法采用的8*8图像块会导致图片质量严重下降,而JPEG2000的效果此时会明显更好。
因为JPEG2000在获取同等质量图像时更为费劲,所以它对JPEG来说并没有明显优势。事实上,目前只有少数网站支持显示JPEG2000图像。它的优势在于,当处于增加算法复杂度不再是问题的环境下,可以为图像提供灵活的格式。
例如利用小波变换能以不同分辨率有效重组图像,用户可肉眼迅速大量搜索低分辨率的图片。JPEG2000允许用户指定区域以高分辨率展示,通常是出于医学成像的需要。最后,它也使得数码图像能以JPEG2000的格式存储在相机内存卡中,这样在拍照后,图片会以低分辨率存储起来以减少内存使用。在JPEG面世约十年后,JPEG2000才出现。它还拥有一些其他的功能特性,比如事后图像加密的功能。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Devin Pope,行为科学家。
翻译作者,孙云龙,哆嗒数学网翻译组成员。
校对,mathyrl。。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
一位前谷歌工程师最近提醒了世人,在包括物理、计算机科学和工程学在内的几个数理领域中,女性的比例不足。
造成这一比例偏低的原因引起了激烈的争论,广泛讨论认为进入门槛和考试成绩的性别差异是潜在原因。

但新的数据分析却强调了信心在差距中的重要性。
一些年轻女性, 包括在数学方面特别有天赋的, 往往都会低估自己的能力。
缺乏信心可能会促使这一领域的一些最好的人才去寻求其他成功途径,毕竟, 即使一些人有过人的天赋, 如果她不相信自己是一个天才的数学家, 她也不太可能去喜欢科学、技术、工程、数学的学习生涯,并且以后以此为生。
(顺便说一下, 一些女性发现她们的自信也会受到舆论宣称女性容易成为次等数学家的言论的影响, 但这都是以后的事情了。)
最近, 我偶然发现了一些数据,在我们都特别熟悉的SAT考试中印证了上述观点
当一些高中生们在参加 SAT测试时, 他们都会填写一份人口统计学和其他高中和大学有关问题的问卷。这个问卷的老版本会询问学生对他们自己智力能力的信心。具体来说, 学生们会被问及,他们是否相信自己是数学能力最高的前10%。
使这个设定变得特别有趣的是, 数据不仅包括学生们对自己能力的信心, 还包括他们的 SAT 分数, 而这个分数为实际能力提供了大致的衡量标准。在九十年代末和二十一世纪初, 样本调查使用了超过 400万 SAT 考生的数据, 下图显示了,实际SAT数学成绩每10分为间隔,在每个分数段中相信自己的数学能力排在前10%的男性和女性的比例。
如人所料, 如果学生在SAT数学部分的分数更高 (图中的曲线是向上倾斜的), 他们更有可能相信自己在10%。然而, 这个图表明, 在所有的 SAT 分数水平, 男性比女性对自己的数学能力更有信心。例如, 这个图表明, 达到了700分的男性有67%相信他们的数学能力在前10%, 而女性达到700分的却只有56%的人有相同的信念。这些结果表明, 女性对自己的数学能力的信心是不及相同SAT 数学成绩的男性的。
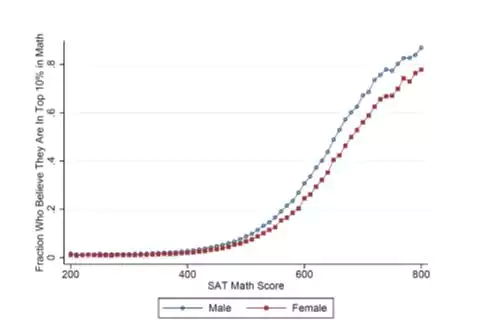
一些人可能会说,这个数据不能说明只在数学学科存在这个性别差异,有可能在所有学科都存在这种差异。幸运的是, 数据能够说明,男性比女性更自信到底是一个普遍现象,还是在数学学科中有一些特殊的数据表现。
下图显示了大约 400万SAT考生对通过他们的SAT语文分数他们是否相信自己的写作能力在10%这个问题的回答,不像数学能力图表, 在这里我们可以明显看到, 在取得相同 SAT 成绩时,女性比男性对自己的写作技巧更有信心。因此, 不是在所有科目中, 男性都比女性更有信心。相反, 数学能力似乎是一个特殊的学科, 男性和女性表现出信心上的巨大差别。
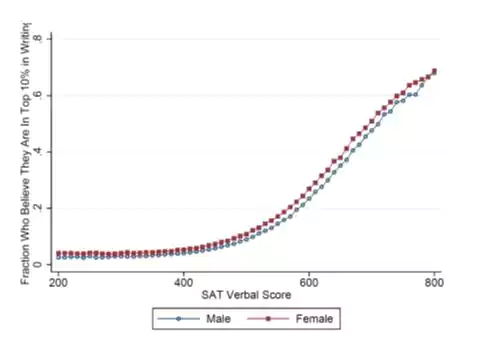
这些数据在一个熟悉的领域给人提供了令人信服的证据, 证明了即便能考出相同的分数,男性和女性在数学能力上的自信程度也是存在差异的。这些信心的差异可能是造成大学专业学生和职业人员中性别失衡的一个重要因素。精准的在提高数学信心上做工作, 或许是科学、技术、工程、数学内解决性别失衡方面问题的一项重要手段。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 数学上下三万年(五):十九世纪上半叶的数学
这个时期欧美基本完成工业革命,各种科学学科开始按现代的门类分化,并影响到社会学科。中国也在这个时期进入半殖民地半封建社会。
本期出场人物有:高斯、勒让德、热尔曼、傅里叶、泊松、拉普拉斯、柯西、阿贝尔、哈密顿、狄利克雷、洛巴切夫斯基、雅克比、刘维尔、德摩根、埃尔米特等。
本系列下面是往期内容:
1800年,拉克鲁瓦(Lacroix)完成了他的三卷本教科书《微分学与积分学》(Traité de Calcul differéntiel et intégral)的出版。
1801年
高斯出版了《算术研究》(Disquisitiones Arithmeticae)。它包含了七部分,前六部分研究数论,最后一部分研究正十七边形尺规作图。
1801年
谷神星被发现然后不知所踪。高斯从少量已有的观测资料计算了它的轨道,随后几乎恰好在高斯预测的位置上谷神星被重新发现。
1801年
高斯证明了费马的猜想,即每个正整数可以表为三个三角数之和。

1803年
拉扎尔·卡诺(Lazare Carnot)出版了《位置几何学》(Géométrie de position),其中首次在几何学中系统地使用了向量。
1804年
贝塞尔(Bessel)发表了一篇关于哈雷彗星轨道的论文,其中使用了200年前哈里奥特的观测数据。
1806年
阿尔冈(Argand)引入了阿尔冈图作为在平面上复数几何表示的一种方法。
1806年
勒让德发展了最小二乘法,用于寻找一组数据的最佳逼近。
1807年
傅立叶(Fourier)发现了用一系列三角函数之和来表示连续函数的方法,并在一篇提交到法国科学院的论文《固体上的热传导》(On the Propagation of Heat in Solid Bodies)中使用了这个方法。

1808年
热尔曼(Germain)对费马大定理作出了重要贡献。这就是被勒让德命名的“热尔曼定理”。
1809年
潘索(Poinsot)发现了两个新的正多面体。
1809年
高斯描述了最小二乘法,在《天体运动论》(Theoria motus corporum coelestium in sectionibus conicis Solem ambientium)中他使用这种方法寻找天体的轨道。
1810年
葛尔刚(Gergonne)出版了他的新数学期刊《纯粹数学与应用数学年刊》(Annales de mathématique pures et appliquées)的第一卷,这个期刊又称为《葛尔刚年刊》(Annales de Gergonne)。
1811年
泊松(Poisson)出版了《力学》(Traité de mécanique)。它包含了泊松关于数学在电磁学与力学的应用的研究工作。
1812年
拉普拉斯(Laplace)出版了两卷本《概率的解析理论》(Théorie Analytique des probabilités)。第一卷研究了生成函数以及概率论中出现的各种表达式的逼近。第二卷包含了拉普拉斯的概率定义、贝叶斯法则与数学期望。
1814年
阿尔冈(Argand)给出了对代数基本定理的一个漂亮证明(带有一些缺陷)。
1814年
巴洛(Barlow)制作了巴洛表,给出了从1到10000的整数的因子分解、平方、立方、平方根、倒数和双曲线对数。
1815年
彼得·罗热(Peter Roget,《罗热同义词词典》的作者)发明了对数计算尺。
1815年
普法夫(Pfaff)发表了关于被称为“普法夫形式”的重要工作。
1816年
皮科克(Peacock),赫歇尔(Herschel)和巴贝奇(Babbage)是剑桥分析学会(Analytical Society)的领袖,该学会出版了拉克鲁瓦(Lacroix)的教科书《微分学与积分学》(Traité de Calcul differéntiel et intégral)的英译本。
1817年
贝塞尔在研究开普勒问题过程中发现了一族被称为“贝塞尔函数”的整函数,以确定三体在相互引力的作用下的运动。
1817年
波尔查诺(Bolzano)出版了《纯分析证明》(Rein analytischer Beweis),试图将微积分从无穷小量概念中解放出来。他不使用无穷小量来定义连续函数。这本著作包含了波尔查诺-魏尔斯特拉斯定理。
1818年
受到拉普拉斯工作的启发,亚德里安(Adrain)发表了地球形态以及不同纬度的重力的研究。
1819年
霍纳(Horner)向皇家学会提交了一篇论文,给出了用于求解代数方程的“霍纳方法”,该论文于同年发表在英国皇家学会哲学汇刊。
1820年
布利安香(Brianchon)发表了《在给定四个条件下,确定等边双曲线的研究》(Recherches sur la determination d'une hyperbole equilatère, au moyen de quatres conditions données),其中包含了九点圆定理的陈述和证明。
1821年
纳维对于不可压缩流体给出了著名的“纳维-斯托克斯方程”。
1821年
柯西(Cauchy)出版了《分析教程》(Cours d'analyse),这是第一次将数学分析建立在正式基础上。它为巴黎综合理工学院的学生设计,致力于尽可能严格地发展微积分的基本定理。

1822年
彭赛列(Poncelet)在《论图形的射影性质》(Traité des propriétés projectives des figures)发展了射影几何的原理。这本著作包含了射影几何的基本思想,例如交比、透视、对合、以及虚圆点。
1822年
傅立叶(Fourier)1811年的获奖作品《热的解析理论》(Théorie analytique de la chaleur)发表。它使得傅立叶分析的技术被广泛地利用,这将广泛应用于数学和整个科学领域。
1822年
费尔巴哈(Feuerbach)发表了他的关于三角形的九点圆的发现。
1823年
鲍耶·亚诺什(János Bolyai)完成了关于非欧几何的一个完整体系的论文的准备工作。当鲍耶发现高斯已经预见到他的大部分工作但没有发表任何东西,他推迟了发表。
1823年
巴贝奇(Babbage)开始制造一台大“差分机”,该机器可以计算对数以及三角函数。他的经验来自于他在1819年至1822年间制造的小“差分机”。
1824年
萨迪·卡诺(Sadi Carnot)出版了《论火的动力,以及合适的机器来开发这个动力》(Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance)。这是一本关于蒸汽机的书,它在热力学中有根本重要性。形成热力学第二定律的基础的“卡诺循环”也出现在这本书中。
1824年
阿贝尔(Abel)证明了高于四次的多项式方程没有根式解。他把这个证明自费出版在一本六页的小册子上。

1824年
贝塞尔对行星扰动进行研究的同时进一步发展了“贝塞尔函数”。
1824年
斯坦纳(Steiner)发展了综合几何学。他在1832年发表了关于这个论题的理论。
1825年
冈珀茨(Gompertz)给出了“冈珀茨死亡率定律”,它表明死亡率呈几何级数增长,因此当死亡率以对数标度绘制时,得到一条直线,称为“冈珀茨函数”。
1826年
安培(Ampère)出版了《关于电动力学现象之数学理论的回忆录,独一无二的经历》(Memoir on the Mathematical Theory of Electrodynamic Phenomena, Uniquely Deduced from Experience)。它包含电动力定律的数学推导,并描述了四个实验。它为电磁理论奠定了基础。
1826年
克雷勒(Crelle)开始出版他的期刊《纯数学和应用数学杂志》(Journal für die reine und angewandte Mathematik),后来被称为“克雷勒杂志”。第一卷包含了阿贝尔的几篇论文。
1826年
彭赛列(Poncelet)关于圆锥曲线极点与极线的工作使他发现了对偶原理。引入了术语“极线”的葛尔刚(Gergonne)独立发现了对偶原理。
1827年
雅可比(Jacobi)在向勒让德写的信中详述了他关于椭圆函数的发现。与此同时,阿贝尔在独立地进行关于椭圆函数的工作。
1827年
莫比乌斯(M?bius)出版了关于解析几何的《重心的计算》(Der barycentrische Calkul)。它成为了经典并包含了他的关于射影几何与仿射几何的很多结果。书中他引入了齐次坐标并讨论了几何变换,特别是射影变换。
1827年
费尔巴哈(Feuerbach)写了一篇论文,独立于莫比乌斯引入了齐次坐标。
1828年
高斯引入了微分几何并发表了《关于曲面的一般研究》(Disquisitiones generales circa superficies)。这篇论文来源于他对测地线的兴趣,它包含了“高斯曲率”等几何思想。这篇论文也包含了高斯著名的“绝妙定理”(theorema egregrium)。
1828年
格林(Green)出版了《论应用数学分析于电磁学》(Essay on the Application of Mathematical Analysis to the Theory of Electricity and Magnets),书中将数学应用于电场和磁场的性质。他引入了术语“势”,发展了势函数的性质,并将其应用于电和磁。连接表面积分和体积积分的公式,现在称为“格林定理”,在书中首次出现,“格林函数”也首次出现在书中,该函数被广泛应用于偏微分方程的解。
1828年
阿贝尔开始研究双周期椭圆函数。
1828年
普吕克(Plücker)出版了《解析几何》(Analytisch-geometrische),发展了“普吕克简算记号”。他比莫比乌斯和费尔巴哈早一年独立地发现了齐次坐标。
1829年
伽罗华(Galois)向法国科学院提交了他的第一篇关于方程代数解的作品。
1829年
罗巴切夫斯基(Lobachevsky)发展了非欧几何,特别是双曲几何,他关于这个论题的第一份描述发表在《喀山通讯》(Kazan Messenger)。当它被提交到圣彼得堡科学院时被奥斯特罗格拉德斯基(Ostrogradski)拒绝。
约1830年
巴贝奇(Babbage)创建了用于保险计算的第一个精确精算表。
1830年
泊松在弹性力学中引入了“泊松比”,其中涉及材料的应力和应变。
1830年
皮科克(Peacock)出版了《论代数》(Treatise on Algebra),试图给代数学一个与欧几里德《几何原本》相媲美的逻辑处理。
1831年
莫比乌斯(M?bius)发表了《一大类特殊的反转公式》(über eine besondere Art von Umkehrung der Reihen),书中引入了莫比乌斯函数以及莫比乌斯反演公式。
1831年
柯西(Cauchy)给出了单复变解析函数的幂级数展开。
1832年
斯坦纳(Steiner)出版了《不同几何形式的依赖关系的系统性发展》(Systematische Entwicklungen ...),书中给出了基于度量考虑的射影几何的一种处理。
1832年
鲍耶·亚诺什(János Bolyai)关于非欧几何的工作作为他父亲鲍耶·法尔科斯的书的附录发表。
1833年
勒让德指出了关于平行公设的12个“证明”中的缺陷。
1834年
哈密顿(Hamilton)在《动力学中的一种普遍方法》(On a General Method in Dynamics)使用代数来处理动力学。这篇论文给出了应用于动力学的特征函数的第一个陈述。
1835年
凯特勒(Quetelet)出版了《论人类及其能力之发展》(Sur l'homme et le développement de ses facultés)。他提出了“平均人”的概念,认为平均人是根据正态曲线对人类特征测量的中间值。
1835年
科里奥利(Coriolis)出版了《物体系的相对运动方程》(Sur les équations du mouvement relatif des systèmes de corps)。他引入了“科里奥利力”,并证明,如果在运动方程中添加一个称为“科里奥利加速度”的额外的力,那么运动定律适用于转动参考系。同年科里奥利出版了一本关于台球的数学理论的著作。
1836年
奥斯特格拉斯基(Ostrogradski)重新发现了格林定理。
1836年
刘维尔创办了数学杂志《纯粹与应用数学杂志》(Journal de Mathématiques Pures et Appliquées),这份杂志有时被称为《刘维尔杂志》(Journal de Liouville),记录了19世纪法国数学的一部分重要内容。
1836年
彭赛列(Poncelet)出版了《力学在机械中的应用》(Cours de mécanique appliquée aux machines)。它第一次提出了将数学应用于机械设计。
1837年,泊松出版了《关于判断的概率之研究》(Recherches sur la probabilité des jugements)。在书中他确立了概率的法则,给出了“泊松大数定律”,并且对于二项分布一种限制情形的离散随机变量描述了“泊松分布”。
1837年
《剑桥与都柏林数学杂志》开始出版。
1837年
狄利克雷(Dirichlet)给出了函数的一般定义。
1837年
刘维尔(Liouville)讨论了积分方程,并给出了“斯图姆-刘维尔定理”用于求解此类方程。
1837年
旺策尔(Wantzel)证明了经典问题倍立方与三等分角不可能用尺规作图。
1838年
贝塞尔(Bessel)测量了天鹅座61的视差,这是第一颗被计算视差的恒星。
1838年,库诺特(Cournot)出版了《财富理论的数学原理之研究》(Recherches sur les principes mathématiques de la théorie des richesses),书中讨论了数学经济学,特别是供需函数。
1838年
德摩根(De Morgan)发明了术语“数学归纳法”,并使该方法精确化。
1839年
拉梅(Lamé)证明了费马大定理在n=7的情形。
1840年
柯西出版了四卷本《分析与数学物理习题集》(Exercises d'analyse et de physique mathematique)的第一卷。
1841年
高斯发表了一篇光学论文,其中给出了一个公式,用于计算给定焦距的透镜成像的位置和大小。
1841年
雅可比(Jacobi)撰写了《函数行列式》(De determinantibus functionalibus),致力于研究函数行列式,现在称为雅可比行列式。
1841年
凯特勒(Quetelet)建立了比利时中央统计局。
1842年
海森(Hesse)在一篇研究三次和二次曲线的论文中引入了“海森行列式”。
1842年,斯托克斯(Stokes)开始研究流体,出版了《关于不可压缩流体的稳定流动》(On the steady motion of incompressible fluids)。
1843年
哈密顿(Hamilton)发现了四元数,它是复数的四维推广。
1843年
刘维尔(Liouville)向法国科学院宣称他发现了伽罗华的未发表作品中的深刻结果,并承诺将伽罗华的论文以及他自己的注解发表出来。
1843年
库默尔(Kummer)在研究唯一分解时发明了“理想复数”。这导致了环论的发展。
1843年
凯莱(Cayley)在他的论文中研究了“n维几何”,他是第一个研究高维几何的人。他使用行列式作为主要工具。
1844年
刘维尔找到了第一个超越数,这种数不能被表示为有理系数代数方程的根。
1844年,格拉斯曼(Grassmann)出版了《线性外代数,数学的新分支》(Die lineale Ausdehnundslehre, ein neuer Zweig der Mathematik),其中他发展了一种代数的思想,用特定的法则来处理表示几何对象的符号,例如点、线、面等。
1845年
凯莱出版了《线性变换理论》(Theory of Linear Transformations),其中他研究了线性变换的复合。
1845年
柯西在研究置换群的时候证明了一个群论基本定理,后来被称为“柯西定理”。
1846年
刘维尔在《Liouville's Journal》(刘维尔杂志)发表了伽罗华的关于求解代数方程的论文。
1846年
14岁的麦克斯韦(Maxwell)写了他的第一篇论文《论卵形线与其他多焦点曲线》(On the description of oval curves, and those having a plurality of foci)。
1847年
布尔(Boole)出版了《逻辑的数学分析》(The Mathematical Analysis of Logic),其中他证明了逻辑法则可以用数学方法处理而非形而上学。布尔的工作为计算机逻辑奠定了基础。
1847年
德摩根(De Morgan)提出了两个集合论定律,被称为“德摩根律”。
1847年
斯陶特(Von Staudt)出版了《位置几何学》(Geometrie der Lage)。它第一次将射影几何从度量基础中完全解脱出来。
1848年
汤姆森(开尔文勋爵)提出了以他名字命名的绝对温标。
1849年
埃尔米特(Hermite)将柯西的留数技术应用到双周期函数。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 数学上下三万年(四):欧洲资产阶级革命开启
本期发布的编年史涵盖1640年到1800年的内容。1640年,应该开始资产阶级革命。而中国在此时进入清朝。本期四大数学家出场三个:牛顿、欧拉、高斯。
本期出场人物有:帕斯卡、费马、托里拆利、惠更斯、胡克、牛顿、莱布尼兹、伯努利家族、泰勒、棣莫弗、欧拉、阿涅西、拉格朗日、高斯等。
本系列下面是往期内容:
1640年
帕斯卡(Pascal)出版了《圆锥曲线专论》(Essay pour les coniques)。
1641年
威尔金斯(Wilkins)出版了关于编码和密码的著作。
1642年
帕斯卡(Pascal)制造了一台计算器帮助他父亲进行税务计算。它只能做加法。

1644年
托里拆利(Torricelli)出版了《几何操作》(Opera geometrica),包括了他在抛射体方面的成果。他研究了费马点(到三角形三个顶点距离之和最短的点)。
1647年
费马(Fermat)声称他证明了一个定理但页边没有足够的空位写下证明的细节。这就是后世所知的费马大定理:当正整数n>2时,关于x,y,z的不定方程x^n + y^n = z^n 没有非零整数解。这个定理最终在1994年由怀尔斯证明。
1647年
卡瓦列里(Cavalieri)出版了《六个几何练习》(Exercitationes geometricae sex),其中首次包含了xn从0到a的积分。
1648年
威尔金斯(Wilkins)出版了《数学的魔法》(Mathematical Magic),给出了一些机械装置的说明。
1648年
亚伯拉罕·博斯(Abraham Bosse)出版了一本著作,其中包含了著名的“笛沙格定理”:当两个三角形是透视时,则其对应边的交点共线。
1649年
凡司顿(Van Schooten)出版了《笛卡尔几何》的第一个拉丁文版本。
1649年
德博纳(De Beaune)撰写了《简明注释》(Notes brièves),它包含了很多“笛卡尔几何”的成果,特别是给出了现在熟知的双曲线,抛物线,椭圆的方程。
1650年
德·维特(De Witt)完成了《曲线论》(Elementa curvarum linearum)。它是首次对直线和圆锥曲线的解析几何的系统性发展。这本书直到1661年才发表,出现在凡司顿的主要著作的附录中。
1651年
墨卡托(Nicolaus Mercator)出版了三本关于三角学和天文学的专著:《对数球面三角学》(Trigonometria sphaericorum logarithmica),《宇宙志》(Cosmographia),和《球面天文学》(Astronomica sphaerica)。他给出了ln(1 + x)的级数展开,
1653年
帕斯卡出版了关于帕斯卡三角形的《论算术三角》(Treatise on the Arithmetical Triangle)。帕斯卡三角形已被很多早期数学家研究过。
1654年
费马和帕斯卡在夏季交换的五封信里得出赌博和概率的规律。
1654年
帕斯卡出版了关于流体静力学的《论液体平衡》(Treatise on the Equilibrium of Liquids)。他认识到力通过流体均等地向各个方向传递,并给出帕斯卡压力定律。
1655年,布隆克尔(Brouncker)给出了4/π 的一个连分数展开。他也给出了双曲线的求积法,这个成果在三年后发表。
1656年
沃利斯(Wallis)出版了《无穷小算术》(Arithmetica infinitorum),其中使用了插值法计算积分。
1656年
惠更斯(Huygens)取得了第一个摆钟的专利。
1657年,惠更斯出版了《论赌博中的计算》(De ratiociniis in ludi aleae)。这是第一本关于概率论的出版著作,基于费马和帕斯卡在1654年的信件中的想法首次概述了数学期望的概念。
1657年
奈勒(Neile)在修正三次抛物线的时候,首次找出一种代数曲线弧长。
1657年
德·班西(Frenicle de Bessy)出版了《问题解答》(Solutio duorm problematum),给出了费马的一些数论挑战问题的解答。
1658年
雷恩(Wren)找出了旋轮线的弧长。
1659年
拉恩(Rahn)出版了《代数》(Teutsche algebra),其中包含了÷(除号),这个符号可能是佩尔(Pell)所发明。
1660年
德·斯路斯(De Sluze)在他的作品中讨论了螺线,拐点,以及求几何平均。他研究了被帕斯卡命名为“斯路斯明珠”的曲线。
1660年
胡克(Hooke)发现了胡克定律。
1660年
维维亚尼(Viviani)测量了声速。他确定了旋轮线的切线。
1661年
凡司顿(Van Schooten)出版了第二卷,也是最后一卷的《笛卡尔几何》(Geometria a Renato Des Cartes)。这项工作将解析几何确立为一个重要的数学专题。这本书还包括他的三位弟子德·维特(de Witt),胡德(Hudde)和休雷特(Heuraet)所做的附录。
1662年
伦敦皇家学会成立。布隆克尔当选第一任会长。
1662年
约翰·葛兰特(Graunt)和威廉·配第(Petty)出版了《对死亡率表的自然与政治观察》(Natural and Political Observations made upon the Bills of Mortality)。它是最早的统计学书籍之一。
1663年
巴罗(Barrow)成为英国剑桥大学首任卢卡斯数学教授。
1665年
牛顿(Newton)发现二项式定理并开始了关于微积分的工作。
1666年
法国科学院在巴黎成立。
1667年
詹姆斯·格雷戈里(James Gregory)出版了《论圆和双曲线的求积》(Vera circuli et hyperbolae quadrature),为无穷小几何形成了严格的基础。
1668年
詹姆斯·格雷戈里出版了《几何的通用部分》(Geometriae pars universalis),这是撰写微积分教科书的首次尝试。
1668年
佩尔(Pell)给出了100000以内所有正整数的因子表。
1669年
雷恩(Wren)发表了他的成果:旋转双曲面是一个直纹面。
1669年
巴罗退去剑桥大学卢卡斯数学教授席位,他的学生牛顿被任命。
1669年
沃利斯(Wallis)出版了《力学》(Mechanica),这是一份对力学的详细数学研究。
1670年
巴罗出版了《几何学讲义》(Lectiones Geometricae),其中包含了他关于切线的重要工作,这形成了牛顿微积分工作的起点。
1671年,德·维特(De Witt)出版了《关于人寿年金》(A Treatise on Life Annuities)。它包含了数学期望的想法。
1671年
詹姆斯·格雷戈里(James Gregory)发现了泰勒定理并将自己的发现写信告诉柯林斯(Collins)。他用arctan(x)的级数展开得到了的π/4的级数。
1672年
门戈利(Mengoli)出版了《化圆为方问题》(The Problem of Squaring the Circle),其中研究了无穷级数并给出了π/2的无穷乘积展开式。
1672年
莫尔(Mohr)出版了《欧几里得》(Euclides danicus),其中他展示了所有单用圆规也能作出的用尺规能作出的欧氏几何结构。
1673年
莱布尼茨(Leibniz)向皇家学会演示了他的半成品计算器。它能够做乘法,除法,开方。
1673年
惠更斯出版了《钟摆论》(Horologium Oscillatorium sive de motu pendulorum)。除了钟摆的工作之外,他还研究了曲线的渐屈线和渐伸线,并发现旋轮线和抛物线的渐屈线。
1675年
拉海尔(La Hire)出版了《圆锥曲线》(Sectiones conicae),这是关于圆锥曲线的重要著作。
1675年
莱布尼茨(Leibniz )首次使用了积分的当代记号。
1676年
莱布尼茨独立于牛顿发现了基本函数的微分。
1677年
莱布尼茨(Leibniz )发现了积、商的微分法则以及函数的函数。
1678年
乔瓦尼·塞瓦(Giovanni Ceva)出版了《曲线》(De lineis rectis),其中包含了塞瓦定理。
1678年
科克尔(Cocker)的《算术》(Arithmetic)在他去世两年后出版。这本书在大约100年的时期里达到了100个版本以上。
1679年
莱布尼茨(Leibniz )引入了二进制算术。但直到1701年才发表。
1680年
卡西尼(Cassini)研究了“卡西尼卵形线”,是平面内到两个定点的距离之积为常数的点的轨迹
1682年
钦豪斯(Tschirnhaus)研究了反射焦散曲线:一个光源发出的光线从一条给定曲线的反射光线的包络线。
1683年
関孝和在他发表的著作中首次引入了行列式。他研究了ax - by = 1的整数解,其中a,b是整数。
1684年
莱布尼茨在《一种求极大值与极小值和求切线的新方法》(Nova Methodus pro Maximis et Minimis, itemque Tangentibus)中发表了他的微积分的详述。它包含了我们熟悉的d记号(微分),以及计算幂、积、商的导数的法则。
1685年
沃利斯(Wallis)出版了《代数》(De Algebra),包含了牛顿二项式定理的最早描述。它也使哈利奥特的卓越贡献为人所知。
1685年
科翰斯基(Kochanski)给出了求圆周长的一种近似方法。
1687年
牛顿出版了《自然哲学的数学原理》(The Principia or Philosophiae naturalis principia mathematica)。这本书被公认为有史以来最伟大的科学著作。牛顿提出了关于运动,重力和力学的理论。他的理论解释了彗星的偏心轨道,潮汐及其变化,地球轴线的进动和月球的运动。
1690年
雅各布·伯努利(Jacob Bernoulli)首次使用“积分”一词描述曲线下的面积。
1690年
罗尔(Rolle)出版了关于方程理论的《代数学》(Traité d'algèbre)。
1691年
雅各布·伯努利发明了极坐标,一种使用角度和距离描述空间中点的位置的方法。
1691年
罗尔出版了《等式解法》(Méthods pour résoudre les égalités),其中包含了罗尔定理。他的证明使用了胡德(Hudde)的方法。
1692年
莱布尼茨引入了术语“坐标”。
1693年
哈雷(Halley)出版了波兰城市布雷斯劳(现弗罗茨瓦夫)的死亡率表。他试图将人口中的死亡率和年龄相关联,并证明在未来人寿保险精算表的生产中具有非常大的影响力。
1694年
约翰·伯努利(Johann Bernoulli)发现了洛必达法则。
1696年
约翰·伯努利(Johann Bernoulli)提出了最速降线问题(Brachristochrone),并挑战其他人来解决这个问题。约翰·伯努利,雅各布·伯努利和莱布尼兹都解决了这个问题。
1702年
大卫·格雷戈里(David Gregory)出版了《物理学和天文学的几何原理》(Astronomiae physicae et geometricae elementa),这是牛顿理论的一个普及读本。
1706年
琼斯(Jones)在他的《新数学引论》(Synopsis palmariorum matheseos)中引入了希腊字母π来表示圆周长和直径之比。
1707年
牛顿出版了《广义算术》(Arithmetica universalis),包含了他在代数学的成果的汇编。
1707年
棣莫弗(De Moivre)使用三角函数将复数表示为r(cos x + i sin x)的形式。
1708年
拉海尔算出了心脏线的长度。
1710年
阿布丝诺(Arbuthnot)在皇家学会发表了一份重要的统计报告,其中讨论了男婴出生率轻微超越了女婴出生率。这篇论文是概率在社会统计的首次应用。
1711年
乔瓦尼·塞瓦(Giovanni Ceva)出版了《关于金钱问题》(De Re Nummeraria),数理经济学的最早期作品之一。
1713年
雅各布·伯努利(Jacob Bernoulli)的书《猜想的艺术》(Ars conjectandi)是概率的重要工作。它包含了出现在指数级数讨论中的伯努利数。
1715年
布鲁克·泰勒(Brook Taylor)发表了《增量的直接与间接方法》(Methodus incrementorum directa et inversa),这是对微积分的重要贡献。该书讨论了微分方程的奇异解,变量替换公式,以及函数导数与反函数导数的关联。还有关于振动弦的讨论。
1717年
约翰·伯努利(Johann Bernoulli)表明虚移位的原理适用于所有的均衡情况。
1718年
雅各布·伯努利(Jacob Bernoulli)关于变分法的工作在他去世后发表。
1718年
棣莫弗(De Moivre)出版了《机会的学说》(The Doctrine of Chances)。统计独立性的定义与骰子和其他游戏的许多问题一起在该书出现。他还研究了死亡率统计数字和年金理论的基础。
1719年
布鲁克·泰勒(Brook Taylor)出版了《线性透视原理》(New principles of linear perspective),这本书的第一版在四年前以书名《线性透视论》(Linear perspective)出现。这项工作首次对消失点(vanishing points)进行一般的处理。
1722年
科茨(Cotes)未完成工作在他去世后发表为《调和计算》(Harmonia mensurarum)。它涉及有理函数的整合。它包含了微积分应用于对数和圆函数的彻底处理。
1724年
雅各布·黎卡提(Jacopo Riccati)在一篇论文中研究了黎卡提微分方程。他对雅各布·伯努利首先研究过的方程的某些特殊情形给出解法。
1724年
俄国皇家科学院在圣彼得堡建立。
1727年
欧拉(Euler)被指派到圣彼得堡。他在手稿《关于最近所做火炮发射试验的思考》(Meditation upon Experiments made recently on firing of Cannon)中引入符号e表示自然对数的底数。这份手稿直到1862年才发表。

1728年
格兰迪(Grandi)出版了《几何之花》(Flora geometrica)。他给出了形如花瓣和花叶的曲线的几何定义。例如,玫瑰曲线被这样命名是因为它们看起来像玫瑰,而克利曲线(Clelia curve)是以伯爵夫人克利·博罗梅奥(Clelia Borromeo)命名的,他将他的书献给了伯爵夫人。
1730年
棣莫弗(De Moivre)给出了他的关于复数三角表示的进一步的定理。他也给出了斯特林公式(Stirling's formula)。
1731年
克莱罗(Clairaut)出版了关于偏斜曲线的《关于双重曲率曲线的研究》(Recherches sur les courbes à double coubure)。
1733年
棣莫弗(De Moivre)在《二项式(a+b)^n的展开级数之和的近似算法》(Approximatio ad summam terminorum binomii (a+b)^n in seriem expansi)首次描述了正态分布曲线,又称为误差定律。随后在1820年,高斯也研究了正态分布。
1733年
萨凯里(Saccheri)在《欧几里得无懈可击》(Euclides ab Omni Naevo Vindicatus)进行了早期的关于非欧几何工作,尽管他认为这是试图证明欧几里德平行公设。
1734年
贝克莱(Berkeley)出版了《分析学家:或致一位不信神的数学家》(The analyst: or a discourse addressed to an infidel mathematician)。他认为,虽然微积分导出了正确的结果,但是它的基础并不比宗教信仰更安全。
1735年
欧拉引入了记号f(x)。
1736年
欧拉解决了柯尼斯堡七桥问题。他在数学上证明了不可能设计出一种走法使得七条桥都恰好通过一次。
1736年
欧拉出版了《力学》(Mechanica),这是第一本基于微分方程的力学教科书。
1737年
辛普森(Simpson)为他的私人学生出版了《论流数》(Treatise on Fluxions)。在书中他使用无穷级数来求函数的定积分。
1738年
丹尼尔·伯努利(Daniel Bernoulli)发表了《流体力学》(Hydrodynamica)。它首次给出了从容器的孔流出的水的正确分析,并讨论了泵和其他机械来使水升高。他在第10章中给出了气体动力学理论的基础。
1739年,达朗贝尔(D'Alembert) 出版了《微积分实录》(Mémoire sur le calcul intégral)。
1740年
辛普森出版了《机会的本质与规律》(Treatise on the Nature and Laws of Chance)。这本概率论著大部分是基于棣莫弗的工作。
1740年
麦克劳林(Maclaurin)因他在运用引力理论解释潮汐现象的工作获得了法国科学院的头等奖。
1742年
麦克劳林出版了《论流数》(Treatise on Fluxions),旨在通过采用希腊几何的方法为微积分提供严格的基础。这是牛顿方法的第一个系统性的阐述,这些方法是作为对贝克莱对微积分缺乏严格基础的攻击的答复。
1742年
哥德巴赫(Goldbach)在一封写给欧拉的信中猜想每个大于或等于4的偶数可以写成两个素数之和。哥德巴赫猜想仍然没有被证实。
1743年
达朗贝尔(D'Alembert)出版了《动力学》(Traité de dynamique)。在这部著名的作品中,他阐述了他的原理:运动中的刚体系统的内部行为和反应是处于平衡状态的。
1744年,达朗贝尔(D'Alembert)出版了《论流体的平衡与运动》(Traite de l'equilibre et du mouvement des fluides)。他将他的原理应用到流体的平衡与运动中。
1746年
达朗贝尔(D'Alembert)在首次尝试证明代数基本定理的过程中,进一步发展了复数理论。
1747年
达朗贝尔在《关于风的一般成因的沉思》(Réflexion sur la cause générale des vents)使用偏微分方程研究风,因此获得普鲁士科学院奖。
1748年
阿涅西(Agnesi)写了《分析讲义》(Instituzioni analitiche ad uso della giovent italiana),这是一本意大利语的微积分教材。这本书包含了许多精心挑选的例子来说明想法。其中研究了一条被称为“阿涅西的女巫”的曲线。
1748年
欧拉出版了《无穷的分析》(Analysis Infinitorum),这是数学分析的入门。他定义了函数并表明数学分析是函数的研究。这项工作是将微积分基于初等函数的理论而不是几何曲线。著名的公式e^(πi) = -1在这本书中首次出现。
约1750年
达朗贝尔研究了“三体问题”并将微积分应用到天体力学。欧拉、拉格朗日和拉普拉斯也进行三体问题的工作。
1750年
克莱姆(Cramer)出版了《代数曲线分析导论》(Introduction à l'analyse des lignes courbes algébraique)。这本书研究曲线。在第三章研究了曲线的一个分类并给出了著名的“克莱姆法则”。
1750年
法尼亚诺(Giulio Fagnano)在《数学成果》(Produzioni matematiche)发表了他以前的大部分工作。它包含了双纽线的显著性质以及积分的加倍公式。欧拉利用这个公式证明了椭圆积分的加法公式。
1751年
欧拉发表了他的复数对数理论。
1752年
达朗贝尔在研究流体动力学的时候发现了柯西-黎曼方程。
1752年
欧拉公布了多面体定理:V-E+F=2。
1753年
西姆松(Simson)注意到斐波那契数列中相邻两项之比趋近于黄金分割比例。
1754年
拉格朗日(Lagrange)对等时降线做出了重要的发现,这将大大推动变分法这个新学科。
1755年
欧拉出版了《微分学原理》(Institutiones calculi differentialis),书的开头包含了有限差分的研究。
1757年
以拉格朗日为首的一批科学家,在意大利成立了一个数学协会,这是都灵皇家科学院的前身。
1758年
1758年12月25日,哈雷彗星的出现印证了哈雷的预测。此时哈雷已去世15年。
1759年
爱皮努斯(Aepinus)出版了《电磁理论的尝试》(Tentamen theoriae electriciatis et magnetismi)。这是第一本发展电磁数学理论的著作。
1761年
兰伯特(Lambert)证明了π是无理数。他在1768年发表了一个更一般的结果。
1763年
蒙日(Monge)开始了画法几何的研究。
1764年
贝叶斯(Bayes)出版了《机会问题的解法》(An Essay Towards Solving a Problem in the Doctrine of Chances),其中给出了贝叶斯概率理论。它包含了重要的“贝叶斯定理”。
1765年
欧拉出版了《刚体运动理论》(Theory of the Motions of Rigid Bodies),它为分析力学打下了基础。
1766年
兰伯特撰写了《平行线理论》(Theorie der Parallellinien),它是对平行公设的研究。他通过假定平行公设是错的,从而推导出了大量关于非欧几何的结果。
1767年
达朗贝尔把因未能证明平行公设而造成的初等几何的问题成称为“初等几何的丑闻”。
1768年
兰伯特发表了π是无理数的结果。
1769年
欧拉出版了他的三卷本《屈光学》(Dioptics)的第一卷。
1769年
欧拉提出了欧拉猜想,即三个四次幂的和不是一个四次幂,四个五次幂的和不是一个五次幂,高次幂依此类推。
1770年
拉格朗日证明了任意正整数可表为四个平方数之和。
1770年
拉格朗日出版了《关于方程代数解的思考》(Réflexions sur la résolution algébrique des équations),这是一个对于最高次数为四次的方程存在根式解的原因的基础研究。该论文首先将方程的根视为抽象量而不是数字。他研究了根的置换,这项工作导致了群论。
1770年
欧拉出版了教科书《代数》(Algebra)。
1771年
拉格朗日证明了威尔逊定理(首先由华林(Waring)提出但未给出证明),即n是素数当且仅当(n - 1)! + 1被n整除。
1774年
布丰(Buffon)使用一种数学与科学的方法来计算地球的年龄大约为75000年。
1777年,欧拉在一份手稿中引入符号i表示-1的平方根,这跟手稿直到1794年才出版。
1777年,布丰(Buffon)实施了他的概率实验:通过将小棍子投掷到瓷砖地板上,并计算小棍子与瓷砖线条的相交次数,从而计算π。
1779年,裴蜀(Bézout)出版了关于方程理论的《代数方程通论》(Théorie générale des équation algébraiques)。这本书包含了一个现在被称为“裴蜀定理”的结果。
1780年
拉格朗日因为研究行星对彗星轨道的扰动的工作获得了法国科学院的最高奖。
1781年,库仑(Coulomb)因为研究摩擦力的工作《论简单机械》(Théorie des machines simples)获得了法国科学院最高奖。
1781年
威廉·赫歇尔(William Herschel)发现了天王星。
1783年
爱丁堡皇家学会成立。
1784年
勒让德(Legendre)在他的天体力学著作《关于行星形状的研究》(Recherches sur la figure des planètes)引入了“勒让德多项式”。
1785年
孔多塞侯爵(Condorcet)出版了《论多数派决策的概率分析的应用》(Essai sur l'application de l'analyse à la probabilité des décisions rendues à la pluralité des voix)。这是社会科学概率研究的重大进步。
1785年
勒让德提出了二次互反律,但他的证明不正确。
1785年
孔多塞侯爵(Condorcet)出版了《论多数派决策的概率分析的应用》(Essay on the Application of Analysis to the Probability of Majority Decisions),这是在概率论发展过程中的极其重要的工作。
1785年
拉格朗日开始了关于椭圆函数和椭圆积分的工作。
1788年
拉格朗日出版了《分析力学》(Mécanique analytique)。它总结了自牛顿时期以来在力学领域完成的所有工作,值得注意的是它使用微分方程理论。通过这项工作,拉格朗日将力学转化为数学分析的一个分支。
1792年
德·普隆尼(De Prony)开始主要制作《地籍图》(Cadastre)。它由精确到14至29位小数的对数与三角函数表组成。
1794年
勒让德出版了关于几何的《几何学原理》(Eléments de géométrie),它将是接下来100年的重要著作。它将在欧洲大部分地区以及随后的译本和在美国取代欧几里得的《几何原本》作为教科书。它成为后来的几何课本的原型。
1796年
拉普拉斯(Laplace)在《宇宙系统论》(Exposition du systeme du monde)提出了着名的星云假说,它将太阳系视为起源于大型、扁平和缓慢旋转的炽热气体的收缩和冷却。
1796年
高斯(Gauss)给出了二次互反律的首个正确证明。

1797年
拉格朗日出版了《解析函数论》(Théorie des fonctions analytiques)。它是第一本研究单变量实变函数理论的论文。它使用现代记号,例如dy/dx表示导数。
1797年
韦塞尔(Wessel)提出了一篇关于复数的向量表示的论文,该论文在1799年用丹麦语发表。这个想法出现在1787年他所写的一份报告中。
1797年,马歇罗尼(Mascheroni)在《圆规几何》(Geometria del compasso)中证明了所有点尺规作图都能单由圆规来完成,这时直尺是多余的。
1797年
拉扎尔·卡诺(Lazare Carnot)出版了《关于无穷小分析的形而上学的思考》(Réflexions sur la métaphysique du calcul infinitésimal),书中把零和无穷作为极限来处理。他认为无穷小量是真实的对象,可以表示为极限的差。
1799年
高斯证明了代数基本定理,并注意到早期的证明,例如达朗贝尔在1746年的证明,可以很容易修正。
1799年
拉普拉斯出版了五卷本《天体力学》(Traité de mécanique céleste)的第一卷。它应用微积分研究天体的轨道,并检验太阳系的稳定性。
1799年
蒙日(Monge)出版了《画法几何学》(Géométrie descriptive),描述了正投影,这是现代机械制图中使用的图形化方法。
1799年
鲁菲尼(Ruffini)发表了高于四次的代数方程没有根式解的第一个证明。这个证明以及他后来在1803年,1808年和1813年发表的进一步的证明很大程度上都被忽视了。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
俄罗斯人民友谊大学的客座教授Durvudkhan Suragan和他的团队已经得到并证明了一类新的泛函不等式。哈代不等式是一类数学物理中重要的问题。研究的结果发表在《数学进展》(Advances in Mathematics)杂志上。
所谓哈代不等式(Hardy's inequalities)的性质已经被全世界的数学家研究了将近一个世纪。它们是级数和积分之间某种特定的关系。在泛函分析中哈代不等式被当做工具用来研究数学和力学中的很多问题。同时在退化微分方程理论(椭圆型偏导数)、谱理论、非线性分析以及插值理论中具有应用。
哈代不等式的以及其他的类似问题的研究主要是在欧几里得向量空间中进行的。
从更高等的数学角度来看,欧几里得空间是一个给定点乘运算的集合,集合可以由任意元素构成。二维和三维空间是欧几里得空间中特殊的情况。鲁德大学的团队拓展了哈代不等式的理论,通过一种更复杂的数学对象——齐性拓扑群来进行研究。
一个集合被称作拓扑群,如果它既是一个拓扑空间也是一个群,同时乘积算子和取逆元素的运算是连续的。一类拥有特殊性质的子集(拓扑)构成了拓扑空间。除了这些子集,拓扑包括了任意数量的这些子集的并集,,以及交集(仅限于有限个子集)和空集。一个群结构的存在意味着这个集合有着相关的代数运算,它包括所谓的“恒等元”(在乘法中有1的性质),以及所有的元素都有逆元。
现有的在一个齐性拓扑群中建立泛函不等式方法是基于研究范数的性质。数学中的范数是一个满足特定要求的非负复合函数。复数的模和向量长度是简单的范数例子。研究作者提出的新方法允许使用随机范数,而不是过去使用的严格确定和固定复合函数。
团队的研究结果是在齐性群上建立了一类新的哈代不等式类型。它的一个特殊应用就是阿贝尔群上的分析学。阿贝尔性(或者交换性)表现为一个群运算的结果独立于元素的顺序。一个关于交换性的特殊例子就是众所周知的法则“改变求和数的求和顺序不会改变和”。科学家指出最新的取得公认的不等式可能被应用在非线性微分方程理论中。
研究的结果主要是理论性和基础性的。现有的哈代型不等式分析结果已被重新考虑并扩展到新的数学对象群体中。因此,对于这些不等式更多未知的应用可能会被发现。
参见:Michael Ruzhansky et al. Hardy and Rellich inequalities, identities, and sharp remainders on homogeneous groups, Advances in Mathematics (2017). DOI: 10.1016/j.aim.2017.07.020
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Kevin Hartnett,量子杂志资深作家。
翻译作者,我是崔小白,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
两位数学家已经证明了两个不同的无穷其大小是相等的,解决了数学界一个长期存在的问题。他们的证明建立在无穷的大小和数学理论的复杂性之间意外的联系上。

在一项颠覆了几十年传统智慧的突破中,两位数学家证明了两种不同的无穷大实际上大小相等。这一进展涉及到数学中最著名、最棘手的问题之一:自然数的无穷与实数的无穷之间是否存在别的无穷。
这个问题早在一个世纪前就被发现了。当时数学家们知道“实数比自然数多,但不知道多多少。实数的无穷是刚刚好比自然数大的那个无穷,还是它和自然数之间还有别的无穷?”芝加哥大学的马利亚里斯(Maryanthe Malliaris)说,他与耶路撒冷希伯来大学和罗格斯大学的萨哈龙·希拉一起合作完成了这项新工作。
在他们的新工作中,马利亚里斯和希拉(Shelah)解决了一个70年没解决的相关问题,即一个无穷大(称为p)是否小于另一个无穷大(称为t)的大小判定问题。他们证明了两者实际上是相等的,这让数学家感到意外。
“当然,无论是我个人观点,还是之前大家的看法,都认为p应该小于t,”希拉说。

马利亚里斯和希拉去年在“美国数学学会杂志”上发表了他们的证明,并在去年七月荣获了集合论领域的最高奖项之一。然而他们的工作远远超出了这两个无穷数的相关问题。它为无限集合的大小和另一个不同邻域数学理论复杂性之间开辟了一条意想不到的联系通道。
多种无穷
无穷的概念令人费解。那么会不会存在很多大小不同的无穷呢?这可能是有史以来最违反直觉的数学发现。然而当我们用一个配对的游戏来解释的时候,连小孩子都能理解。
假设你有两组物体,或者两组“集合”,就像数学家所说的那样:一组汽车和一组司机。如果每辆车只有一个司机,没有空车,没有司机留下,那么你就知道汽车的数量等于司机的数量(即使你不知道这个数字是多少)。
在19世纪后期,德国数学家乔治·康托在数学的形式语言中领会到了这种匹配策略的精髓。他证明了两个集合当它们可以一一对应时,它们大小是相同的,或者说它们具有相同的“基数”——即当每辆车只有一个司机时。也许更令人惊讶的是,他证明了这种方法也适用于无限大的集合。
考虑自然数:1、2、3等等。自然数的集合是无限的。但是对于偶数和质数的集合呢?每一个集合起初看起来都是自然数的一个较小的子集。实际上,在数轴上的任何有限长度上,都有大约一半的偶数是自然数,而质数的数目则更少。
然而无限集的表现却不同。康托表示这些无限集的元素之间存在一一对应关系。
1 2 3 4 5 … (自然数)
2 4 6 8 10 … (偶数)
2 3 5 7 11 … (质数)
正因为如此康托得出的结论是,三个集合都是一样大。数学家把这个大小的集合称为“可数的”,因为您可以为每个集合中的每个元素标记一个编号。
在确立无限集的大小之间可以进行一一对应的比较后,康托做出了一个更大的飞跃:他证明了一些无限集其实比自然数集更大。
考虑实数,也就是数轴上的所有点。 实数有时被称为“连续统”,反映了它们的连续性:在一个实数与下一个实数之间没有空隙。康托能够证明实数不能与自然数进行一一对应:即使在创建了一个将自然数与实数相匹配的无限列表之后,总是可以拿出另一个不在你的列表上的编号的实数。 因此他得出结论:实数集合大于自然数集合。于是第二种无穷诞生了:即不可数无穷。

然而有个问题康托始终无法解决,即是否存在一个中间大小的无穷——介于可数的自然数集的大小和不可数的实数集之间。他认为没有,这是一个现在被称为连续统假设的猜想。
在1900年,德国数学家希尔伯特列出了数学中最重要的23个问题。他把连续统假设放在首位。“这似乎在说,我们迫切的想知道这个问题的答案,”马利亚里斯说。
在这之后的一个世纪,尽管数学家们拼尽全力,这个问题本身已经证明它是史无前例的难以攻克。介于中间的那个无穷存在吗? 我们可能永远都不知道。
力迫法证明
在整个20世纪上半叶,数学家试图通过研究出现在许多数学领域的各种无限集来解决连续统假设。他们希望通过比较这些无穷大之间的大小,可以开启对自然数的大小和实数的大小之间可能存在的中间数的间隔的理解。
这些无穷大的大小判定研究,很多被证明对连续统假设没有用。在20世纪60年代,数学家保罗·科恩解释了其中的原因。 科恩提出了一种叫做“力迫”的方法,证明了连续统假设独立于数学公理,也就是说,在集合论的框架内是无法证明的。 (科恩的工作补充了库尔特·哥德尔1940年的工作,哥德尔的成果表明连续统假设不能用通常的数学公理来否定它。)
科恩的工作成果于1966年为他赢得了菲尔兹奖(数学最高荣誉之一)。数学家随后用力迫法来解决在前半个世纪中所提出的无穷之间的许多大小判定,表明这些大小判定也不能在集合论框架得到肯定或否定的回答。(具体来说,ZF(策梅洛-弗兰克尔)集合论加上选择公理。)
然而有些问题仍然存在,其中包括20世纪40年代提出的关于p是否等于t的问题。p和t都是两个无穷有序集的大小,它用精确的(而且似乎是唯一的)方法量化了自然数极小子集族的大小。
两个集合大小的细节并不重要。更重要的是数学家们很快就发现了p和t大小的两种情况,首先,两组都比自然数大。第二,p总是小于等于t,因此如果p小于t,那么p就是一个中间的无穷——介于自然数和实数的大小之间。那连续统假设便是错误的了。
简单的说说这个问题是什么:p是一个具有“强有限交性”和没有“伪交性”的自然数无穷子集合组成集族的最小的无穷,这意味着其中的子集以一个特定的方式相互重叠;t称为“塔数”并且是按“反向几乎包含”且没有“伪交性”的自然数无穷子集合组成的集族的最小大小的有序集合的无穷。
数学家之前倾向于认为p和t之间的关系不能在集合论框架内被证明,但是他们也不能确定问题的独立性。p和t之间的关系几十年来一直处于这种未确定的状态。 直到马利亚里斯和希拉涉及别的研究领域后,才最终找到了解决办法。
复杂性的序
当保罗·科恩用力迫法证明了连续统假设在通常的数学框架之外的时候,模型论领域正在开展一项截然不同的工作。
对于模型论家来说,“理论”是定义数学领域的一套公理或规则。你可以将模型论视为一种对数学理论进行分类的方式——对数学源代码的探索。威斯康星大学麦迪逊分校数学退休教授H·杰罗姆·基斯勒说:“我认为人们有兴趣对理论进行分类的原因是他们想要了解一些特定事情在不同数学领域里发生的真正原因。”
1967年,基斯勒介绍了现在所谓的基斯勒序,这个序关系试图根据数学理论的复杂性将其进行分类。 他提出了一种衡量复杂性的技术手段,并试图证明数学理论至少可以分为两类:最小复杂性和最大复杂性。基斯勒说:“这是一个小起点,但是我的感觉就是这里有无穷的类。
在基斯勒建立基斯勒序十多年后,希拉发表了一本有影响力的书,其中包括一个重要的章节,证明了复杂性中有自然发生的跳跃——具有较大复杂性的理论与较小复杂性理论之间可能存在一条明确的分割线。而此后30的年,基斯勒序的研究几乎没有任何进展。
一个理论具有复杂性,其意义并不总是那么显而易。这个领域的很多工作在某种意义下是如何让大家直观的理解这些问题。基斯勒将复杂性描述为一种理论中可能发生的事情的范围,如果一个理论较之于另一个理论中可能发生的事情越多,我们就说前者理论更复杂。
然后,在她2009年的博士论文和其他早期论文中,马里亚里斯重新开始了关于基斯勒序的工作,并为其作为分类程序的权提供了新的证据。 2011年,他和希拉开始合作,旨在更好地理解序的结构。 他们的目标之一是依托基斯勒的标准,找到更多的性质,构造出具有最大复杂性的理论。
马里亚里斯和希拉尤其关注两个特别的性质。他们已经知道其中一个会导致极大的复杂性。他们想知道另一个是否也如此。随着他们工作的进展,他们意识到这个问题与p和t是否相等的问题是平行相关的。2016年,马里亚里斯和沙拉发表了一篇60页的论文,解决了这两个问题:他们证明了这两个特性是具有相同复杂性的(它们都导致了最大的复杂性),并且证明了p等于t。
“不知不觉中,一切都准备就绪,”马里亚里斯说。“然后问题就顺理成章的解决了。”
今年七月,马利亚里斯和希拉被授予豪斯多夫奖(Hausdorff Medal),集合论的最高奖项之一。这项荣誉印证了他们证明是一个令人惊奇的结果,也印证了他们证明的强大力量。因为在集合论的框架内证明p和t不相等是不可能的,大多数数学家曾经期望p可以小于t。马利亚里斯和希拉证明了两个无穷大是相等的。 他们的工作也表明,p和t之间的关系比数学家之前知道的要深奥得多。
“我觉得如果有一天人们意外地发现两个基数相等,那么该证明可能是令人惊讶的,但那可能是一个简短而睿智的论证,不涉及建立任何实体的机制。”康奈尔大学的数学家贾斯汀·摩尔(Justin Moore)说到,他发表了一篇有关马利亚里斯和希拉的证明的概述。
相反,马利亚里斯和希拉证明了p和t是相等的,通过在模型论和集合论之间开辟一条通路,并已经在这两个领域开辟了新的研究前沿。他们的研究也最终解决了数学家们希望能够帮助解决连续统假设的问题。然而专家们的压倒性的感觉是,无法解决的连续统假设是错误的:虽然无穷在很多方面的性质异于常态,如果在已发现的无穷之间没有更多大小不同的无穷,那么这太不同寻常了。
澄清:在9月12日,本文进行了修改,以澄清20世纪上半叶的数学家想知道连续统假设是否属实。 正如文章所述,这个问题在很大程度上取决于保罗·科恩的工作。
我们哆嗒补录的番外篇:
这篇文章提到的问题叫做极小塔问题(The Minimal Tower Problem),收录在科学出版社出版的《10000个科学难题(数学卷)》中,我们把这一页截图呈上。

遗憾的是我们偶然发现这里居然有笔误。这里两个箭头,左边一个箭头的α不应该写在下标位置,应该写在正常位置。而右边箭头的α其实写错了,应该是a 。我们已经把这个问题向出版社反馈了。
另外,文章中提到的连续统基数的确定的问题,是一个更加诡谲的问题。这书里也有介绍,标题叫做《连续统势确定问题》。
总体来说,这本书是本非常好的收录当代数学难题的工具书。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Alex Doak,伦敦大学学院流体力学博士。
翻译作者,溦之洸茫,哆嗒数学网翻译组成员。
校对,我是崔小白。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
希腊:留克特拉 (公元前371年)
出于对至高权力的渴望,古希腊的各城邦总是在不断经历战火的洗礼。在一阵短暂的和平后,当时的霸权斯巴达公然挑战底比斯的政治地位。由于底比斯拒绝解散由其主导重建的彼奥提亚邦联同盟(Boeotian Confederacy),斯巴达对其宣战。底比斯城以及她的盟友聚集了7200名重装步兵(hoplites),由将军埃帕米侬达(Epaminondas)率领,来到了留克特拉的地界,在那里等待他们的是9600名斯巴达重装步兵。

此时斯巴达国王克莱奥姆波洛图斯(Cleombrotus)情绪十分阴郁,尽管近期在军事上有过胜利,然而在前往留克特拉的行军路上已经显现了凶兆,尤其是因为献祭给神灵的动物被狼吃了。然而在对手下各个将军进行询问之后,发现他们都确信斯巴达能够取得胜利。现在他召唤你这个奇怪的旅行者,希望通过你的惊人洞察力帮助他分析未来。

一对一战斗及兰彻斯特线性律
在所有的数学建模中,如果希望得到有意义的结果,我们必须理解所模拟战斗过程的基本机制。在这个例子中,我们需要对古希腊战争有更好的了解。希腊城邦的部队主要是有重装步兵组成。在战斗中,这些人采用的是‘臭名昭著’的方阵队列:士兵们组成数排密集的横向队列,手持长矛和盾牌迎击他们的敌人。每一支部队同时前行,最勇敢和最有战斗经验的军人是在前排,这样才能保证行进的队伍不会减速和逃窜。两军接触后,盾牌互砸,长矛互戳,血肉横飞,尸横遍野……最终,在经受一定的兵力损失后,一方的队形完全崩溃,士兵开始大量逃窜,最终不可避免地被击败。
对于这一类的战斗,兰彻斯特首次给出了一个简单的模型,他假设军队的交战是由一对一的形式进行的。也就是说,每名士兵只和与他对应的那一名敌军士兵交战,没有参与打斗的士兵在后排静静等待着他们战斗回合的到来。假设军队数量在时间t内是连续的。斯巴达军队士兵数S(t)及底比斯军队士兵数T(t)的变化率可以表示为:

其中,N指的是在某一时间双方各自的交战人数。我们已知克莱奥姆波洛图斯国王的方阵是由希腊重步兵组成的标准12排方阵,那么第一排就有9600/12=800人。同时,克莱奥姆波洛图斯国王认为底比斯军队为了避免侧翼被包抄,会采用同是每排800人的9排的方阵来迎击自己的军队。古希腊时期战斗的一个典型特点是伤亡相对较低,我们可以假设如果任意一方士兵数不足以维持6排阵列(即T<4800或S<4800),士兵就会产生恐慌情绪进而逃窜。
K_T和K_S分别表示两只军队的战斗力。如果K_T=1 (K_T表示K的下标是T,下文相应情况类似),意味着单位时间内,每一位在战斗的底比斯士兵都杀死了一名斯巴达士兵;如果K_T=0,表明没有底比斯士兵杀死斯巴达人。兰切斯特杀伤率(Lanchester attrition rates ,即K_T和K_S)不一定要为常数:它们可以是与时间有关的(战斗进行过程中士兵会变疲劳),或是依赖于S和T的数值(以寡敌众会扼杀士兵的希望,或是使它们更加拼命战斗)。不过,为了简单起见,我们认为这两个参数是常数。
那么问题来了:战斗中底比斯人的表现要比对手斯巴达人好出多少才能保证自己取得胜利?
我们建立的耦合系统非常容易求解,用(1)式除以(2)式,得到

对上式积分,并将S与T的初值带入,得到
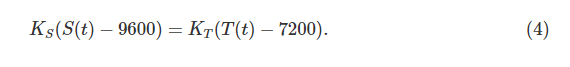
请注意,上述方程体现了军队中士兵数和他们总的战斗力是呈线性关系的(即著名的兰彻斯特线性律)。这是因为我们采用了一对一的战斗模型假设。底比斯要取得胜利,换言之在某一时间t^*(t^*表示t的下标是*,下文相应情况类似),S(t^*)=4800且T(t^*)>4800,将S(t)=4800带入方程(4),并重新写出T的表达式,代入T(t)>4800,可以得到底比斯取得胜利的条件为
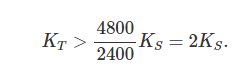
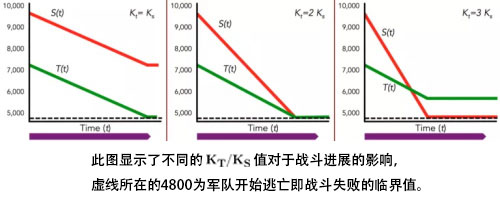
将这些信息呈给克莱奥姆波洛图斯国王,你除了看到他的自信之外并不能提供什么帮助:斯巴达人是当时最勇猛的战士,尽管他的盟军并不是这种最高质量的军队,那也没有理由认为他们会比底比斯的彼奥提亚联合军“弱”两倍。(译者注:这里的弱两倍指K_S/K_T<0.5,也就是K_T/K_S>2)
远程的战斗:瞄准火力和兰彻斯特平方律
尽管希腊战场主要是重步兵的舞台,双方军队还是会拥有一些轻装部队(通常来说是非希腊籍的雇佣兵),他们被称为轻装步兵,(peltasts,此文文中可理解为远程步兵)。他们携带标枪和投石索,在战斗中向敌人投掷射击。轻步兵主要用于袭扰敌人两翼,除了几个非常特殊的战例之外,他们对战局不起决定作用。同样,我们让斯巴达的500名轻步兵与底比斯1000名轻步兵交锋,看看会发生什么。
在这种场合下,我们用到的模型是兰切斯特瞄准火力模型。斯巴达轻步兵P(t)及底比斯轻步兵Q(t)的变化率可以表示为:

这是因为标枪手间的战斗不再是一对一了。相反地,所有士兵可以在同一时间向敌人射击。(译者注:这里的“一对一”不是强调是否是两个人的单打独斗,而是指同一时间能够向敌人攻击的人数,在前面(1)、(2)方程的耦合系统中,某一时刻在进攻敌人的人数为定值N,(5)、(6)方程中这个值是此时刻尚存的人数。这也就是线性律和平方律的本质区别所在。)因此,P的死亡率等于向他们射击的Q的数值乘以一个系数α。同样,这里的变量α_Q不一定为常数,通常来讲在非瞄准射击的情况下,它是与P(即Q可以攻击的目标数)成正比的。简单起见,我们依然认为这两个参数为常数。
将(5)式除以(6)式,得到
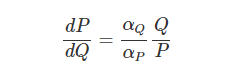
通过分离变量法解微分方程,并带入初始条件,得到
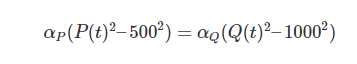
人数与总战斗力由线性关系变成了平方关系,这就是著名的兰彻斯特平方律。从这个等式中我们可以看出,数量要比质量更重要。比敌方人数少一半的斯巴达轻步兵的战斗效率要达到敌方的四倍(α_P/α_Q>4)才能与其打成平手。这些等式是在1916年第一次世界大战时推导出的,或许可以解释当时的人们对军事的一些想法。
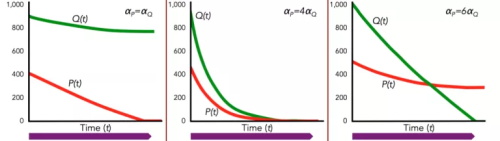
战斗当天
部队:这是战斗中的一个传统,因为士兵的左手绑着盾牌,前进中他们会有向右偏移的趋势,将精锐部队放在右翼可以遏制这种趋势。埃帕米侬达将自己的精锐部队放在左翼,这样以来他可以尽快消灭斯巴达军队的精锐,以免拖到后期己方在人数上的劣势会成为大问题。
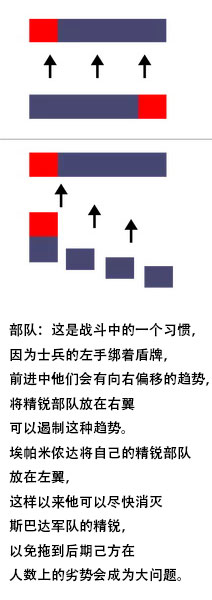
吃完早餐并享用了一点葡萄酒之后,克莱奥姆波洛图斯国王和他的军队来到了留克特拉的开阔平地。国王和他最勇猛的战士位于右翼。可以看到远处的底比斯人正在缓缓接近,扬起一阵尘土。遭遇战首先在两军的轻步兵之间展开,此时两军的重步兵间还有一段距离。随着底比斯军队的靠近,克莱奥姆波洛图斯国王发现不对劲:底比斯人不按套路出牌,在斯巴达军队的右翼方向聚集了一个50排的队列。这50排队列冲到了克莱奥姆波洛图斯国王所在的位置。开始并没什么作用:残酷的战斗是在前排进行的,正如兰彻斯特线性律,双方都死伤惨重。然而随着战斗的进行,很显然50人纵深的底比斯军队不可能被仅仅12排的斯巴达人打败。目睹了斯巴达精锐部队一点点消亡并最终溃散,斯巴达的友军也开始效仿,竞相逃离战场,尽管在此时他们面对的敌人数还是比己方少的。和很多斯巴达士兵一样,克莱奥姆波洛图斯国王也被杀死了,斯巴达在希腊的统治地位画上了一个血腥的句号。
对模型的一点说明
兰彻斯特方程是人口种群建模中非常简单的一个例子,在对很多其他‘捕食者-猎物相互作用系统(其中最经典的要算是狐狸和兔子)’的建模中也有类似的方程。当然完全不必局限于两个“物种”,“物种”也不一定非要为有生命的有机体。
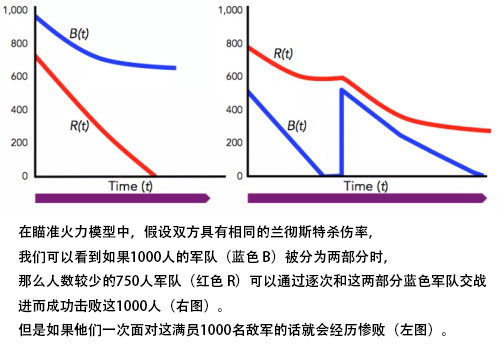
这些方程看上去太简单了,以至于他们并不能真正反映战争的形态。其中最突出的弱点就是兰彻斯特杀伤率。把一支军队的能力简化为一个不依赖于时间和空间的常数,这个假设真的很难被人认可。况且,该模型还要求两方军队都是同类的(也就是说所有部队在计算中都要被认为是一致的)。同时,这也反映了埃帕米侬达的精明之处:他并不把敌人简单地看作清一色的9600名重步兵,而是看作一小队斯巴达人加上一大堆没什么大用的盟友。依靠“擒贼先擒王”的策略,埃帕米侬达在军队人数上的劣势就不是什么问题了。正如J-K Anderson所说:“战场上双方军队中相当大的一部分和观众没什么区别”。
尽管这个模型有着缺陷,但是平方律揭示了瞄准火力模型比一对一模型更加有趣的特性。在瞄准火力的攻击情况下,将人数较多的军队分为两部分,让人数较少的军队逐次和这两部分军队交战,那么人数较少的军队也会取得胜利。这种战术会在线性律的模型下失效:如果斯巴达的盟友并未逃离战场,那么历史可能会被重新书写!
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 数学上下三万年(三):大航海时代
本期发布的编年史主要涵盖15世纪到17世纪,这在欧洲是大航海时代。航海和交易的需求,促进了数学的发展。而中国在同时期处于明朝,民间开始禁止研究天文学,另外到了明朝中后期,开始流行经世之学。
本期出场人物有:哥白尼、卡尔达诺、韦达、开普勒、伽利略、纳皮尔、费马、笛卡尔等。
本系列下面是往期内容:
1470年
许凯(Chuquet)撰写了《算术三编》(Triparty en la science des nombres),这是最早的法文代数书。
1472年
普尔巴赫(Peurbach)发表《行星的新理论》(Theoricae Novae Planetarum)。他使用托勒密的行星本轮理论,但他相信它们是由太阳控制。
1474年
约翰·缪勒(Regiomontanus)发表了他的《星历表》(Ephemeris),为1475年至1506年的天文表,并提出了利用月球计算经度的方法。
1475年
约翰·缪勒发表了《论平面与球面三角形》(De triangulis planis et sphaericis),该书研究球面三角学并将它应用到天文学。
1482年
坎帕努斯(Campanus of Novara)版本的《几何原本》成为第一本印刷的数学书。
1489年
魏德曼(Widman)撰写了德语的算术书,其中首次出现了“+”、“-”号。
1494年
卢卡·帕西奥利(Pacioli)出版了《算术、几何、比例总论》(Summa de arithmetica, geometria, proportioni et proportionalita),是对整个数学的总结,覆盖了算术,三角,代数,货币和度量衡表,赌博,复式记账法和欧氏几何概述。
1514年
范德·赫克( Vander Hoecke )使用“+”,“-”号。
1515年
希皮奥内·德尔·费罗(Del Ferro)发现求解一元三次方程的公式。
1522年
滕斯托尔(Tunstall)出版了《论计算的艺术》(De arte supputandi libri quattuor),这本算术书基于帕西奥利的《算术、几何、比例总论》。
1525年
鲁道夫(Rudolff)在他的书《物术》(Die Coss)中引入了一个类似√的符号表示平方根,这是第一本德语代数书。他理解x的零次方等于1。
1525年
丢勒(Dürer)出版了《度量四书》(Unterweisung der Messung mit dem Zirkel und Richtscheit),这是第一本用德语出版的数学书。它是关于几何结构的著作。
1533年
弗里修斯(Frisius)发表了使用三角学进行精确勘测的方法。他是第一个提出三角测量法的人。
1535年,塔尔塔利亚(Tartaglia)独立于费罗解出了一元三次方程。
1536年
雷吉乌斯(Hudalrichus Regius)找到第五个完全数。这个数2^12·(2^13 - 1) = 33550336是自古代(已发现四个完全数)以来被发现的第一个完全数。
1540年
费拉里(Ferrari)发现了一元四次方程求根公式。
1541年,雷蒂库斯(Rheticus)出版了他的三角函数表和哥白尼工作的三角学部分。
1543年,哥白尼(Copernicus)出版了《天体运行论》(De revolutionibus orbium coelestium)。它给出了哥白尼学说的一个完全阐述,即太阳(不是地球)位于宇宙的中心。

1544年
施蒂费尔(Stifel)出版《整数算术》(Arithmetica integra),其中包含了二项式系数和记号+, -, √。
1545年
卡尔达诺(Cardan)出版了《Ars Magna》(大术),给出三次方程一般解法的公式(基于塔尔塔利亚的工作)和费拉里发现的四次方程一般解法的公式。
1550年
里斯(Ries)出版了他的著名算术书《运算的变革和突破》(Rechenung nach der lenge, auff den Linihen vnd Feder)。它同时使用老的算盘方法和新的印度方法教授算术。
1551年
雷科德(Recorde)翻译和简化古希腊数学家欧几里得的《几何原本》,名为《知识之途》(Pathewaie to Knowledge)。
1555年
沙博(J Scheybl)给出了第六个完全数2^16·(2^17 - 1) = 8589869056,但他的工作直到1977年才为人所知。
1557年
雷科德出版了《砺智石》(The Whetstone of Witte),它将=(等号)引入了数学。他使用这个符号“因为没有其它东西比之更相等的了”(bicause noe 2 thynges can be moare equalle)。
1563年
卡尔达诺撰写了关于赌博的书《论掷骰子》(Liber de Ludo Aleae),但直到1663年才出版。
1571年
韦达(Viete)开始出版《数学法则》(Canon Mathematicus),他打算把它作为他的天文学论著的数学导引。它涵盖了三角学,包含三角函数表及其构造背后的理论。
1572年
邦贝利(Bombelli)出版了他的《代数学》的前三部分。它是第一个给出复数计算法则的人。
1575年
莫罗利科(Maurolico)出版了《算数》(Arithmeticorum libri duo),其中包含了归纳证明的例子。
1585年
斯蒂文(Stevin)出版了《论十进》(De Thiende),书中他对十进制小数给出了初等的和彻底的阐述。
1586年
斯蒂文出版了《静力学原理》(De Beghinselen der Weeghconst),书中包含了力的三角形定理。
1590年,卡达迪(Cataldi)使用连分数来寻找平方根。
1591年,韦达撰写了《分析艺术导论》(In artem analyticam isagoge),使用字母作为已知量和未知数的符号。他用元音字母表示未知数,辅音字母表示已知量。笛卡尔后来引入了字母表末尾的字母x,y ...表示未知数。
1593年
阿德里安·范·罗门(Van Roomen)计算π到16位小数。
1595年
皮蒂斯克斯(Pitiscus)成为第一个在印刷出版物中使用术语“三角学”的人。
1595年
克拉乌(Clavius)撰写《罗马新历之辩》(Novi calendarii romani apologia)为历法改革辩护。
1603年
卡达迪(Cataldi)找到第六个和第七个完全数:2^16·(2^17 - 1) =8589869056 和 2^18·(2^19 - 1) = 137438691328。
1603年
意大利猞猁之眼国家科学院(Accademia dei Lincei)在罗马建立。
1606年
斯涅尔(Snell)首先尝试测量地球表面上的1度子午线弧度,从而确定地球的大小。他出版《数学备忘录》(Hypomnemata mathematica),这是斯蒂文在力学方面的工作的拉丁文翻译。
1609年
开普勒(Kepler)出版《新天文学》(Astronomia nova)。这项工作包含开普勒关于椭圆轨道的第一和第二定律,但只对火星进行了验证。
1610年
伽利略(Galileo)出版了《星际信使》(Sidereus Nuncius),描述了用他制作的望远镜做出的天文发现。哈里奥特(Harriot)也观察到木星的卫星,但没有发表他的工作。

1612年
巴协(Bachet)出版了关于数学谜题和技巧的著作,这将成为几乎所有后来有关数学娱乐的书籍的基础。他设计了一种构建幻方的方法。
1613年
卡达迪(Cataldi)出版了《关于求数的平方根的简易算法》(Trattato del modo brevissimo di trovar la radice quadra delli numeri),其中他用连分数求平方根。
1614年
约翰·纳皮尔(Napier)出版了他的关于对数的著作《奇妙的对数规律的描述》(Mirifici logarithmorum canonis descriptio)。
1615年
开普勒出版了《求酒桶体积之新法》(Nova stereometria doliorum vinarorum),考察酒桶的容积,表面积和圆锥曲线。他在1613年他的婚典上首次产生这个想法。他的方法是微积分的早期应用。
1615年
梅森(Mersenne)鼓励数学家们研究旋轮线。
1617年
斯涅尔发表了他的三角测量技术,提高了制图测量的准确性。
1617年
布里格斯(Briggs)出版了《自然数从1到1000的对数》(Logarithmorum chilias prima),其中引入了以10为底的对数。
1617年
纳皮尔发明了“纳皮尔骨算筹”,这是一个由一些小棒组成的机械计算器。他在《算筹的研究》(Rabdologiae)解释了它们的功能,该书在他去世那年出版。
1620年
比尔吉(Bürgi)出版了《算术与几何进展一览表》(Arithmetische und geometrische progress-tabulen),其中包含了他独立于纳皮尔发现的对数。
1620年
甘特(Gunter)制作了一种机械装置:“甘特式计算尺”,它使用一把尺和一个圆规,基于对数来做乘法。
1620年
古尔丁(Guldin)给出古尔丁质心定理,该定理是帕普斯(Pappus)已经知道的。
1621年
巴协(Bachet)翻译出版了丢番图的希腊文著作《算术》的拉丁文译本。
1623年
施卡德(Schickard)制作了一个“机械钟”,这是一个木制计算器,能做加减法和辅助计算乘除法。他写信给开普勒建议使用机械方式来计算星历表。
1624年
布里格斯出版了《对数的算术》(Arithmetica logarithmica),其中引入了术语“尾数”和“特征”。他给出了自然数1到20000以及90000到100000的对数,计算到14位小数,同时也给出了15位小数的正弦函数表和10位小数的正切及正割函数表。
1626年
吉拉德(Albert Girard)出版了一本三角学论著,其中首次使用了缩写sin,cos,tan。他也给出了球面三角形的面积公式。
1629年
费马(Fermat)从事极大值和极小值的工作,这是对微积分的早期贡献。

1630年
奥特雷德(Oughtred)发明了一种早期形式的圆形计算尺,它使用两个甘特计算尺。
1630年
麦多赫(Mydorge)从事光学和几何学工作。他给出了巴黎的纬度的非常精确的测量。
1631年
哈里奥特(Harriot)的贡献直到他去世十年之后才发表在《分析艺术的实践》(Artis analyticae praxis)。这本书引入了符号>和<表示“大于”和“小于”,但这些符号是由于编辑的工作而不是哈里奥特自己。他在代数方面的工作也非常令人印象深刻,但这本书的编辑没有很好地表现出来。
1631年
奥特雷德(Oughtred)出版了《数学精义》(Clavis Mathematicae),其中包括印度-阿拉伯语记号和十进制小数的描述。它有相当大的一部分是关于代数的。
1634年
罗贝瓦尔(Roberval)找出了旋轮线下的面积。
1635年
笛卡尔(Descartes)发现了多面体欧拉定理:V-E+F=2。
1635年
卡瓦列里(Cavalieri)在他的《连续不可分割的新几何学》(Geometria indivisibilis continuorum nova)发表了他对阿基米德穷举法的发展。该方法结合开普勒无限小几何量的理论。
1636年
费马发现了亲和数对 17296, 18416。这个数对已为800年前的塔比·伊本·夸儿拉所知。
1637年
笛卡尔出版了《几何》(La Géométrie),其中描述了代数在几何中的应用。

1639年
笛沙格(Desargues)开始了射影几何的研究。射影几何考虑了当形状被投影到一个不平行的平面上时会发生什么变化。他在《关于圆锥的平面截面结果的论文草稿》(Brouillon project d'une atteinte aux evenemens des rencontres du Cone avec un Plan)描述了他的想法。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

作者,Math001
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa







关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 数学上下三万年(二):从罗马时代到中世纪
本期出场人物有:托勒密、丢番图、希帕提娅、花拉子米、斐波那契等。
本期中国人出场也不少,他们是:刘歆、刘徽、祖冲之、李淳风、沈括、秦九韶、李冶、杨辉、朱世杰
本系列下面是往期内容:
约公元1年
中国数学家刘歆使用十进制分数。
约公元20年
吉米纽斯(Geminus)撰写了很多天文学著作和《数学理论》(The Theory of Mathematics)。他试图证明平行公设。
约公元60年
海伦(Heron)撰写了《量度论》(Metrica)。书中包含了计算面积和体积的公式。
约公元90年
尼科马库斯(Nicomachus)撰写了《算术入门》(Arithmetike eisagoge),这部著作首次将算术作为一个单独的主题从几何中分离出来。
约110年
梅涅劳斯(Menelaus)撰写了《球面学》(Sphaerica),书中研究了球面三角形和它们在天文学的应用。
约150年
托勒密(Ptolemy)在天文学应用中产生了许多重要的几何成果。他的天文学理论在往后一千多年里被人认可。
约250年
中美洲的玛雅文明使用一种20进制的近似位值数字系统。
250年
丢番图(Diophantus)撰写了《算术》(Arithmetica),是方程关于有理数解的数论研究。
263年
刘徽使用192边的正多边形算出π值为3.14159,精确到小数点后五位。
301年
杨布里科斯(Iamblichus)记述占星术和神秘主义。他的《毕达哥拉斯的生平》(Life of Pythagoras)是一篇引人入胜的传记。
340年
帕普斯(Pappus)撰写了《数学汇编》(Synagoge),该书是希腊几何学的指南。
390年
亚历山大城的塞翁(Theon)写著了一个版本的欧几里德《几何原本》(文字有所修改和补充),之后此书几乎所有的后续版本都是基于此版本。
约400年
希帕提娅(Hypatia)对丢番图、阿波罗尼奥斯的作品做评注。她是第一位有记载的女数学家,她以非凡的学术成就而著名。她成为亚历山大里亚新柏拉图学派的领袖。

450年
普罗克洛斯(Proclus),一位数学家和新柏拉图主义者,是雅典柏拉图学院最后的哲学家之一。
约460年
祖冲之给出π的近似值355/113,精确到小数点后六位。

499年,阿耶波多一世(Aryabhata I)计算π近似值3.1416。他写著了作品《阿里亚哈塔历书》(Aryabhatiya),是关于二次方程,π值和其他科学问题的专著。
约500年
米特罗多勒斯(Metrodorus)汇编了由46个数学问题组成的《希腊选集》(Greek Anthology)。
510年
欧托基奥斯(Eutocius)完成阿基米德的工作的校订与注释。
510年
波爱修斯(Boethius)撰写了几何与算术的著作,著作在很长一段时间内被广泛使用。
约530年
欧多修斯对阿基米德和阿波罗尼乌斯的作品做校订与注释。
532年
数学家安提莫斯(Anthemius)重建位于君士坦丁堡的旧圣索非亚大教堂的。
534年
中国数学被引入到日本。
575年
伐罗诃密希罗(Varahamihira)撰写了《五大历数全书汇编》(Pancasiddhantika)。他对三角学做出了重要贡献。
594年
印度开始使用十进制数字记号。现代数字记号系统就是基于它。
628年
婆罗摩笈多(Brahmagupta)撰写了《婆罗摩历算书》(Brahmasphutasiddanta),一本天文学和数学著作。他使用零以及负数,给出二次方程解法,级数求和,以及求平方根。
644年
李淳风开始选编《算经十书》(亦称《十部算经》)。
约670年
玛雅文明的数学家们在他们的数字系统中引入一个符号表示零。
约775年
阿尔昆(Alcuin)撰写了关于算术,几何和天文学的初级教科书。
约810年
智慧宫在巴格达建立。在那里希腊及印度的数学和天文学著作被翻译成阿拉伯语。
约810年
花拉子米(Al-Khwarizmi)撰写了关于算术,代数,地理和天文学方面的重要著作。特别是《积分和方程计算法》(Hisab al-jabr w'al-muqabala,此书的翻译名称一直在学术界有争议),“代数”(algebra)一词出自“al-jabr”。“算法”(algorithm)出自花拉子米的拉丁文译名“Algoritmi”。

约850年
泰比特·伊本·奎拉(Thabit ibn Qurra)做出了重要数学发现,例如将数的概念扩展到(正)实数,微积分,球面三角学的定理,解析几何,非欧几何。
约850年
泰比特·伊本·奎拉撰写了《论亲和数的确定》(Book on the determination of amicable numbers),其中包含构造亲和数的一般方法。他那时已经知道17296,18416是一对亲和数。。
850年,摩诃毗罗(Mahavira)撰写了《计算精华》(Ganita Sara Samgraha)。它一共九章,包括9世纪中期印度的所有数学知识。
900年
施里德哈勒(Sridhara)撰写了《Trisatika》(亦称《Patiganitasara》)和《Patiganita》(译者注:这两本没有查到标准翻译)。在这些著作中他求解二次方程,求级数和,研究组合数学,给出求多边形面积的方法。
约900年
阿布·卡米勒(Abu Kamil)撰写了《代数》(Book on algebra),研究将代数应用到几何问题。之后斐波那契的工作就是基于这本书。
920年,巴塔尼(Al-Battani)撰写了天文学主要著作《天文星表》(Kitab al-Zij),共57章。它包含了三角学的进步。
950年
热贝尔(Gerbert,也就是后来的教皇西尔维斯特二世)将算盘重新引入欧洲。他使用没有零的印度/阿拉伯数字。
约960年
阿尔·乌格利迪西(Al-Uqlidisi)撰写了《论印度算术》(Kitab al-fusul fi al-hisab al-Hindi),是幸存的最早的显示印度算术系统的书。
约970年
阿布·瓦法(Abu'l-Wafa)发明了象限仪台,用于精确测量天空中星星的偏角。他写了关于算术和几何结构的重要书籍。他引入了正切函数,并产生了改进的计算三角表的方法。
976年
维希拉努斯抄本(Codex Vigilanus)在西班牙出现。它包含了欧洲出现十进制数字的第一个证据。
约990年
卡拉吉(Al-Karaji)在巴格达撰写了《哈法勒》(Al-Fakhri, 意为“荣誉”),该书发展了代数学。他给出了帕斯卡三角形。
约1000年
海什木(Ibn al-Haytham,西方人通常称为Alhazen)撰写了关于光学(包括光学理论和视觉理论)、天文学和数学(包括几何和数论)的作品。他给出了Alhazen问题:给定一个光源和一个球面镜,找到镜子上的点,使得光被反射到观察者的眼睛。
约1010年
比鲁尼(Al-Biruni)撰写了许多科学专题。他的数学工作涵盖算术,级数求和,组合分析,三法则,无理数,比例理论,代数定义,代数方程解法,几何,阿基米德定理,三等分角及其他不能用尺规作图解决的问题,圆锥曲线,立体几何,球极平面投影,三角学,平面中的正弦定理,以及求解球面三角形。
约1020年
伊本·西那(Ibn Sina,欧洲人常称其为Avicenna)撰写了哲学,医学,心理学,地质学,数学,天文学和逻辑学。他的重要数学著作《治疗论》(Kitab al-Shifa) 将数学分为四个主题:几何、天文学、算术和音乐。
1040年
艾哈迈德·纳萨维(Alhmad al-Nasawi)撰写了《印度计算》(al-Muqni'fi al-Hisab al-Hindi),研究了四种不同的数字系统。他解释了算术运算,特别是在每个系统中求平方根和立方根。
约1050年
赫尔曼(Hermann of Reichenau,有时称为Hermann the Lame或Hermann Contractus)撰写了关于算盘和星盘的著作。他向欧洲引入了星盘:一个便携式的日晷和一个带游标的象限仪。
1072年
莪默·伽亚谟(Al-Khayyami,通常称为Omar Khayyam,金庸小说《倚天屠龙记》中小昭唱过他的诗句)撰写了《代数问题的论证》(Treatise on Demonstration of Problems of Algebra),其中包含了具有通过圆锥曲线相交找到几何解的三次方程的完整分类。他测量一年的长度为365.24219858156天,结果非常准确。
1093年
沈括撰写了《梦溪笔谈》,一本数学、天文学、制图学、光学和医学著作。它最早提到指南针。
1130年
贾比尔·阿拉夫(Jabir ibn Aflah)撰写了数学著作,尽管不像其他阿拉伯著作那么好,但由于它们将被翻译成拉丁文,而且可供欧洲数学家使用,因此是重要的。
约1140年
婆什迦罗(Bhaskara II,有时称为Bhaskaracharya)撰写了有关算术和几何的《美丽》(Lilavati)和关于代数的《算术萌芽》(Bijaganita)。
1142年
阿德拉德(Adelard of Bath)从阿拉伯文献翻译了《几何原本》的两到三个译本。
1144年
杰拉德 (Gherard of Cremona )开始将阿拉伯文献(和阿拉伯文的希腊文献)翻译成拉丁文。
1149年
萨马瓦尔(Al-Samawal)撰写了《代数的辉煌》(al-Bahir fi'l-jabr),他用负幂和零的多项式来发展代数。他求解二次方程,求前n个自然数的平方和,并且考察组合问题。
1150年
通过杰拉德翻译的托勒密《天文学大成》(Almagest),阿拉伯数字传入欧洲。正弦函数“sine”出自这个译本。
1200年
中国开始使用代表零的符号。
1202年
斐波那契(Fibonacci)撰写了《算盘书》(Liber abaci),其中列出了他在阿拉伯国家学到的算术和代数。它还引入了现在称为“斐波那契数列”的著名数列。
1225年
斐波那契撰写了《平方数之书》(Liber quadratorum),这是他最令人印象深刻的作品。它是自从一千年前的丢番图的工作以来欧洲数论的第一大主要进步。

约1225年
佐丹劳斯(Jordanus Nemorarius)撰写了天文学作品。在数学中他使用字母,这是早期形式的代数记号。
约1230年
乔安尼斯(John of Holywood,有时称为Johannes de Sacrobosco)撰写了有关算术、天文学和历法改革的作品。
1247年
秦九韶撰写了《数书九章》。它包含同余方程组和中国剩余定理,它也考虑不定方程,霍纳方法,几何图形面积和线性方程组。
1248年
李冶撰写了《测圆海镜》,其中包含负数,通过在数字上加斜画来表示。
约1260年
坎帕努斯(Campanus of Novara),教皇乌尔班四世的牧师,撰写了天文学作品,并发表了欧几里德《几何原本》的拉丁文版,成为之后200年的标准版本。
1275年
杨辉撰写了《乘除通变本末》。它使用十进制分数(以现代形式),并给出了帕斯卡三角形的第一个叙述。
1303年
朱世杰撰写了《四元玉鉴》,其中包含了最高14次的高次方程的多种解法。他还定义了现在所谓的帕斯卡三角形,并展示了如何对某些序列求和。
1321年
列维·本·吉尔森(Levi ben Gerson,有时称为Gersonides)撰写了《数之书》(Book of Numbers),研究算术运算、排列和组合。
1328年
托马斯·布拉德沃丁(Bradwardine)撰写了《论运动中速度的比例》(De proportionibus velocitatum in motibus),这是使用代数学研究运动学的早期工作。
1335年
理查德(Richard of Wallingford)撰写了《论正弦四书》(Quadripartitum de sinibus demonstratis),这是第一部关于三角学的原创拉丁文著作。
1336年
数学在巴黎大学成为学士学位的必修科目。
1342年
列维·本·吉尔森(Gersonides)撰写了《论正弦、弦和弧》(De sinibus, chordis et arcubus),这是一本三角学著作,其中给出平面三角形正弦定理的证明和五个正弦表。
1343年
莫瑞斯(Jean de Meurs)撰写了《数之四书》(Quadripartitum numerorum),一本关于数学、力学和音乐的著作。
1343年
列维·本·吉尔森(Gersonides)撰写了《论数之和谐》(De harmonicis numeris),这是对欧几里德的前五本书的评注。
1364年
尼克尔·奥里斯姆(Nicole d'Oresme)撰写了《Latitudes of Forms》(形式的纬度),这是关于坐标系的早期作品,笛卡尔可能受其影响。奥里斯姆的另一作品中包含了分数指数的首次使用。
1382年
尼克尔·奥里斯姆发表了《天地通论》(Le Livre du ciel et du monde)。这是关于数学、力学和相关领域的论文汇编。奥里斯姆反对地球静止的理论。
1400年
马德哈瓦(Madhava of Sangamagramma)证明了若干无穷级数的结果,给出三角函数的泰勒展开。他利用这些结果得到π的近似值,精确到小数点后11位。
1411年
卡西(Al-Kashi)撰写了《天文科学概要》(Compendium of the Science of Astronomy)。
1424年
卡西撰写了《论圆周》(Treatise on the Circumference),以六十进制和十进制形式给出π的非常好的近似值。
1427年
卡西完成了《算术之钥》(The Key to Arithmetic),它是关于十进制分数的非常深度的工作,它将算术和代数方法应用于解决各种问题,包括几个几何问题,并且是整个中世纪文学时期最好的教科书之一。
1434年
阿尔伯蒂(Alberti)研究三维物体的表现,并撰写关于透视定律的第一部一般性论著《论绘画》(Della Pictura)。
1437年
乌鲁伯格(Ulugh Beg)出版他的《星表》(Zij-i Sultani)。它包含了一个精确到8位小数的三角函数表,基于乌鲁伯格计算1度的正弦值精确到16位小数。
1450年
尼古拉斯 (Nicholas of Cusa)研究几何和逻辑。他对无穷的研究做出了贡献,研究无穷大、无穷小。他将圆看作正多边形的极限。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 数学上下三万年(一):爱在西元前
约公元前30000年
在今天的中欧和法国地区,旧石器时代的人们在骨头上记录数字。
约公元前25000年
早期的几何设计开始运用。
约公元前5000年
十进制数字系统在埃及使用。
约公元前4000年
古巴比伦和古埃及的历法开始使用。
约公元前3400年
首个表示数字的符号以及简单的直线在埃及使用。
约公元前3000年
算珠式计算工具(算盘)在中东和地中海地区出现。
约公元前3000年
象形文字的数字在埃及使用。
约公元前3000年
古巴比伦人开始使用六十进制来记录财务交易。这是一个没有零位值的位值系统。
约公元前2770年
古埃及太阳历开始使用。
约公元前2000年
哈拉帕人采用统一的十进制度量衡。
约公元前1950年
巴比伦人解出了一些特殊的二次方程。
约公元前1900年
莫斯科纸草书成书,也称戈列尼雪夫(Golenishev)纸草书。它提供了古埃及几何的历史细节。
约公元前1850年
古巴比伦人得出毕达哥拉斯定理(在中国称为勾股定理)。
约公元前1800年
古巴比伦人开始使用乘法表。
约公元前1750年
古巴比伦人解决了一些的特殊的线性方程和二次代数方程,编制了平方根表和立方根表。他们掌握毕达哥拉斯定理用法,并用利用数学来扩展天文学知识。
约公元前1700年
兰德(Rhind)纸草书成书,有时也称阿梅斯(Ahmes)纸草书。它表明古埃及数学已经发展了许多技巧来解决问题。乘法基于反复加倍,除法使用连续减半。
约公元前1400年
在这个时期中国开始使用无零的十进制数字系统。
约公元前800年
包德哈亚那(Baudhayana)是古印度最早的绳法经(Sulbasutras)之一的作者。
约公元前750年
马纳瓦(Manava)撰写了一部《绳法经》。
约公元前600年
阿帕斯檀跋(Apastamba)从数学的角度撰写了一部最受人关注的古印度《绳法经》。
公元前575年
泰勒斯(Thales)将巴比伦数学知识带到希腊。他用几何知识来解决问题,例如计算金字塔高度和船只离岸边的距离。
公元前530年
毕达哥拉斯(Pythagoras)移居意大利的克罗顿,并教授数学,几何学,音乐和转世说。
约公元前500年
古巴比伦六十进制数字系统被用于记录和预测太阳、月亮和行星的位置。
约公元前500年
波你尼(Panini)的关于梵语文法的工作是现代形式语言理论的先驱。
.
约公元前465年
希帕索斯(Hippasus)描述了一个“由12个五边形组成的球面”,这涉及到正十二面体。
约公元前450年
希腊人开始使用书面数字。
约公元前450年
芝诺(Zeno)提出著名的芝诺悖论。

约公元前440年
希波克拉底(Hippocrates) 撰写了《原本》(Elements),这是第一本关于几何原理的汇编。
约公元前430年
希庇亚斯(Hippias)发现了割圆曲线,被他用于三等分角和化圆为方问题。
约公元前425年
来自昔兰尼的西奥多罗斯(Theodorus)证明了某些平方根是无理数。这个结果已被前人证明。
约公元前400年
古巴比伦人使用一个符号来表示在楔形文字中记录的数字中的空白位。没有任何迹象表明这被认为是一个数字。
约公元前387年
柏拉图在雅典建立了柏拉图学园。

约公元前375年
来自他林敦的阿契塔(Archytas)发展了力学。他研究“古典问题”倍立方,并将数学应理论用于音乐。他也构建了第一台自动机。
约公元前360年
来自尼多斯的欧多克索斯(Eudoxus)发展了比例理论和穷举法。
约公元前340年
阿里斯泰俄斯(Aristaeus)撰写了《论圆锥曲线五书》(Five Books concerning Solid Loci )。
约公元前330年
奥托里库斯 (Autolycus)撰写了《运行的天体》(On the Moving Sphere),这本书研究球面几何学。它是天文学著作。
约公元前320年
欧德谟斯(Eudemus)撰写了《几何史》(History of Geometry)。
约公元前300年
欧几里德在他的《几何原本》(Stoicheion即The Elements)中给出了几何的系统性发展。他在《反射光学》(Catoptrics)中给出了反射定律。

约公元前290年
阿里斯塔克斯(Aristarchus)使用几何方法来计算太阳和月亮到地球的距离。他也提出了地球绕太阳运动。
约公元前250年
在《论球和圆柱》(On the Sphere and the Cylinder)中,阿基米德(Archimedes)给出了计算球和圆柱体积的公式。在《圆的测量》(Measurement of the Circle)中,他使用允许提高近似精度的方法给出了π的近似值。在《论浮体》(Floating Bodies)中,他提出了现在所谓的“阿基米德原理”,并开始研究流体静力学。他写了有关二维与三维几何的著作,研究圆,球和螺线。他的想法远远领先于他的同时代人,包括一种早期形式的积分的应用。

约公元前235年
埃拉托色尼(Eratosthenes)以非常高的精度估算地球周长,估算值比实际值大了15%。
.
约公元前230年
尼科梅德斯(Nicomedes)撰写了专著《论蚌线》(On conchoids lines),书中包含了他发现的被称为“尼科梅德斯蚌线”的曲线。
约公元前230年
埃拉托色尼发明了埃拉托色尼筛法用于寻找所有素数。
约公元前225年
阿波罗尼奥斯(Apollonius)撰写了《圆锥曲线论》(Conics),书中引入了术语“抛物线”,“椭圆”和“双曲线”。
约公元前200年
戴可利斯(Diocles)撰写了《论燃烧镜》(On burning mirrors),收集了16个几何命题,大部分是关于圆锥曲线的证明。
约公元前200年
中国古典数学著作《九章算术》最早可能出现在这一时期。
约公元前180年
可能是中国最早的数学著作的《算术书》出现在这一时期。
约公元前150年
许普西克勒斯(Hypsicles)撰写了《论星的升起》(On the Ascension of Stars)。书中他首次将黄道划分为360度。
约公元前127年
喜帕恰斯(Hipparchus)发现分点岁差,并计算年份的长度精确到正确值的6.5分钟内。他的天文学工作使用了早期形式的三角学。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
Hello,各位哆嗒粉丝们,今天是元宵节,大家除了吃汤圆应该还会在不同地方参与一些猜谜活动吧。我们哆嗒数学网的小编也为大家奉上20个谜语,祝大家节日愉快!——所有的谜底都和数学有关!
旧时风光雨中新 (猜一数学家)
梦醒时分就踏春 (猜一数学家)
奔跑吧,爸爸的爸爸! (猜一数学家)
一座钟 (猜一数学家)
斗牛牛 (猜一数学名词)
上是一,下是一,中间也是一,就是不是一(猜一数字)
旭日东升 (猜一数字)
扶贫成功 (猜一数字)
谈谈小事 (猜一数学名词)
订立协议 (猜一数学名词)
聚散总无常 (猜一数学名词)
比干的惆怅 (猜一数学名词)
再见了亲爱的妈妈(猜一数学名词)
上帝的抱负 (猜一数学名词)
一样的种子 (猜一数学名词)
失控的风筝 (猜一数学名词)
垂钓 (猜一数学名词)
婚姻法 (猜一数学名词)
止战 (猜一数学名词)
真的十八斤 (猜一数学名词)
我真心希望答案在评论区由各位参与公布。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文来源,牛津大学网站。
翻译作者,Aria,哆嗒数学网翻译组成员。
校对,小米。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
牛津数学家田中佑二(Yuuji Tanaka)描述了他在我们对规范场论的理解的推进上所做的工作:
“规范场论产生自物理,作为一个统一理论,它的出现在杨-米尔斯规范场理论(Yang-Mills gauge theory)和希格斯机制(Higgs mechanism,给物质和作用力关联质量的理论)框架下统一了弱作用(出现在β衰变中)和电磁作用。规范场论在维特曼(Veltman)和特霍夫特(’t Hooft)关于可重整化性质的伟大发现后,成为了粒子物理的主流之一,并给出了实验结果的精确描述。如今所有的基本作用(电磁作用,弱作用,强作用和引力)都可以用规范场论来描述。
这些发展无疑刺激了规范场论的数学研究,尤其是在主丛和向量丛的领域。在这一理论中,联络的曲率对应着规范场的场强。80年代早期,唐纳森(Donaldson)考察了一种特殊的杨-米尔斯规范场(称为自对偶或反自对偶联络)方程的解构成的模空间,并惊人地获得了一种利用模空间或者通过模空间给光滑结构赋予不变量的方法,来区分同胚的四维弯曲空间的不同微分结构。

在唐纳森的工作之后,威腾(Witten)十分巧妙将它地翻译成为特定量子场论的语言。接着阿蒂亚(Atiyah)和杰弗里(Jeffrey)又用数学语言通过马塞-奎伦形式(Mathai-Quillen formalism)重写了威腾的工作。在1994年左右,利用电磁对应的推广(一种电磁理论中隐藏的对称性),这些观点的转变成为了发现赛贝格-威腾方程(Seiberg-Witten equation)与不变量的基石。赛贝格(Seiberg)和威腾(Witten)提出了这项成果在量子级别超杨-米尔斯理论中一个引人注目的应用,即强弱对偶;它使得人们在计算中可以用弱耦合的项来计算强耦合的项)。
瓦法(Vafa)和威腾在更加对称的模型中分析了赛贝格和威腾的工作,并猜测这种情形下不变量的配分函数具有模性质,这是之前提到过的强弱对偶的在数学上的加强。模性质原本是在19世纪椭圆曲线理论中发现的。他们在希格斯场(Higgs fields)退化的假设下用数学的结果在一些例子中检验了该性质。

然而,对于这些理论,尤其包括希格斯场在内,在过去的20年中哪怕一个严格的数学定义也没有被给出。理查德·托马斯(Richard Thomas)和我最近使用了现代代数几何的语言定义了射影曲面的形变不变量;它源自瓦法和威腾理论中规范场论方程解的模空间。我们接着也计算了非退化希格斯场条件下不变量的配分函数。令人惊奇的是,我们的计算结果与瓦法和威腾远在20年之前的猜想完全一致。除此之外,我们的结果也涵盖了曲面上的层。”
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
不得不说,数学从来没有像这样,被所有国家政府如此重视过……
不久前,法国著名的“议员数学家”,2010年菲尔兹奖得主维拉尼,法国教育部督查局总监托罗萨安,以及法国教育部部长布兰克共同发布一份报告,研究如何改进法国的数学教学。并且提出21条建议,提振法国中小学数学教育,以改变当前法国“灾难般”的现状。

据报道,这份报告推荐的改进方案的主要学习对象是新加坡。这个亚洲的城市国家在过去20多年间,数学基础教育水平突飞猛进,成为世界最好的国家之一。而上世纪90年代左右,新加坡的学生数学水平几乎垫底。
“新加坡模式”要做的不仅仅是改变老师给中小学生教授数学的方式,同时还试图让老师他们自己在接受基础教育的时候,能更好的接受数学教育。这回的21条建议,也主要针对提高老师水平方面。
发布报告时作者们强调,这21条并不是一个“奇迹药”,而是一个在其他国家实行多年的一个有效成熟的方案。报告作者们说,在新加坡早期的小学教育中,强调动手操作和实验,然后语言表达,而在这些之后才会进入抽象阶段诸如公式、数、符号的学习。期间还会加入语言和绘画方面的教学内容。
除了提升教师数学水平和课程修改方面的建议。报告人也说,关于这套方案的配套措施也在方案中,比如为学习添加硬件设备和虚拟设备,加入数学相关游戏、竞赛以及课外活动提升学生的数学兴趣,已经采取措施落实在数学学习中男女平等。

法国是从近代起就是数学强国,但是数学精英与普通民众差距甚大。顶端的精英阶层出类拔萃,他们在高水平高中预科班学习,之后进入著名高校。但绝大多数的学生却在师资质量一般,教学水平低下的学校就读。由于高智商的数学天才努力向上流动,进入科研、金融等领域,不愿做中小学教师,结果导致中小学大部分数学教师不得不降低标准录用,由此影响了基础阶段的数学教学。
此次报告发布会的情况,见此链接http://www.education.gouv.fr/cid126423/21-mesures-pour-l-enseignement-des-mathematiques.html (法语)
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
原文作者,Evelyn Lamb,数学普及作家。
翻译作者,Bibliomania,哆嗒数学网翻译组成员。
校对,donkeycn。
当我走进圣艾夫斯,
我见到一个平面有七条线,
每条线有三个点,
(但是一共也只有七个点,)
这首诗并不能很好地描述法诺平面(Fano plane)。
以吾之愚见,法诺平面是最小的有趣的空间。这也许能被扯皮归纳地证伪,但是一个点,或者一些孤立点,并不是有趣的例子。
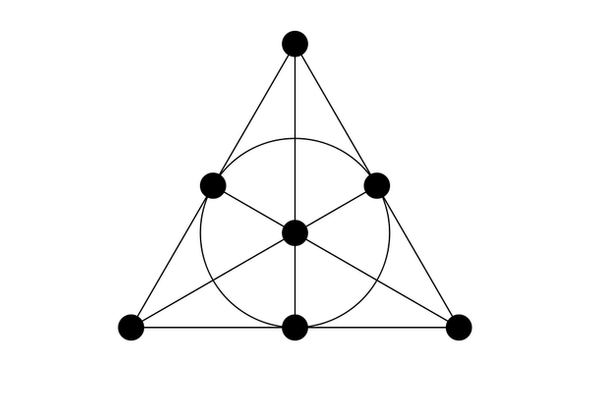
Fano平面有七个分布在七条线上的点。它是射影平面最小可行的例子。
你有没有想过凭什么平面上有些线相交,有些却没有?多么随意啊!不过射影平面就可以把你从这个烦人的问题中拯救出来了,它满足任意两条线都相交。
一个射影平面需要满足下面一些条件。
*每两“点”都有一条“线“连接。
*每条“线”都和其他任何一条“线”相交。
*存在四个点,使得没有一条线过其中两个以上的点。(这个条件并不总是列出来,但是它排除了一些平凡情况,比如说一条线上的两个点或者过一点的几条线。)
有时候数学是靠内心的直觉的,比方说你思考射影几何的时候。(公平来讲,有时候射影几何看起来非常直观,毕竟它的一大应用就是在透视画法上。)你可以把欧几里得平面变成射影平面,通过给每个方向的平行线们添加一个它们所相交的“无穷远”点。所以说有水平方向的无穷远点,有垂直方向的无穷远点,有与水平方向成逆时针47.322度角方向的无穷远点等等。接下来你再让这些无穷远点组成无穷远线。如果你好好想一会,就能明白这样是满足射影平面的要求的。
如果考虑无穷远线上的无数的点让你感到头晕目眩,那法诺平面就是一个更轻松的替代品。它可以简单地看清楚线和点是怎么相交和交互的。
法诺平面是个挑战直觉的东西。当你看到它的图式时,你便会理所当然地认为它有无穷多的点。毕竟它有七条线,我们也都知道,再短的线段,上面也有无穷多的点。
噢不,数学是独裁体系,我们都是独裁者。我们说那七个点就是它仅有的七个点。而这里的”线”并不是由”点”构成的,它们只是公理里规定的“线”而已。另外一个反直觉的地方在于有一条“线”看起来像是个圆,至少在大部分示意图里面都是这样。但如果你都已经接受“线”并不是由无穷多点组成的想法了,那也不难让自己承认这圆真的就是“线”。
法诺平面是最小的有限射影平面。你也许想知道别的射影平面可能的大小。如果我们想让每条线上有4个点而不是3个,我们能找到这样的平面吗?令人惊讶的是,指出射影平面可能的大小并不是一个平凡的问题。(关于术语的说明:我们说法诺平面的阶为2,因为每条线有2+1=3个点,每个点在2+1=3条线上。一般地,一个射影平面阶为N,如果每条线有N+1个点,每个点在N+1条线上。阶为N的射影平面有N²+N+1个点。)我们知道存在阶为任意素数以及任意素数的幂的射影平面,但至于其他数字,我们还有很多工作要做。举个例子,直到上世纪90年代,研究者才确切地证明了不存在阶为10的射影平面,而对于12,仍然是一个开放问题。
虽然有限射影平面看上去像是遗世独立的纯理论的典范,但意外的是法诺平面以及相关的东西居然在博彩方面有所应用。我第一次是在Jordan Ellenberg的《魔鬼数学》(How Not to Be Wrong,又译《数学教你不犯错》)中读到有关的东西的。他举了一个从7个数中选3个的彩票的例子。玩家3个数都猜对的话就获头奖,或者猜对两个数得小奖。
从7个数中选3个,一共有35种可能的组合,所以说你只有1/35的机会中头奖。不过你可以利用法诺平面来增加你猜中两个数的机会。技巧在于买一些彩票但避免同样的数对出现在两张彩票上。你不会想同时买123和234,因为如果2和3猜中了,而你买了它两次了。虽然这意味着两倍的奖金,但也意味着你在其他数对中奖时什么都得不到。
为了在彩票中利用法诺平面中到奖,给7个点依次标上1到7,接着看每条线上的数字。我得到了123, 147, 156, 246, 257, 345, 367.
如果你去验证这些数组,你会发现每个数对都恰好出现了一次。不管中奖的数字是哪些,我们都至少猜中了3个中的两个。如果你标数字的顺序和我不一样,你会得到不同的数组,不过还是有同样的性质。
现在并没有多少彩票只选3个数字了,但花点心思再加上电脑的能力,这个想法可以接着延伸。当然,即使是利用射影平面的聪明策略,在实际彩票购买中使用也不大可能合算。不过如果你感兴趣的话,Ellenberg讲过一个Cash WinFall的故事,其奖品好到足以赢得一些MIT学生的钱。
想了解法诺平面与拉丁方,环面拓扑,纠错码以及其他许多领域的联系,可以查看弗吉尼亚理工大学的Ezra Brown的两篇文章……《(7,3,1)不同的形式集锦》和 《(7,3,1)不同形式的更多集锦》。(链接http://www.math.vt.edu/people/brown/doc/731.pdf ,http://www.math.vt.edu/people/brown/doc/731_more.pdf )
如果八元数乘法的让你感到困顿的话,法诺平面也能帮你记住八元数的乘法规则。最后我忍不住提一句,法诺平面看起来和哈利波特中的死亡圣器的标志惊人地相似。

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
你是不是很多“小学”的数学题目惊到过。网上时不时会冒出一些所谓的“小学奥数”题,加上“难道所有大学生”的标题在网上热传。
这些题目当中其实大多数都不是数学题目,却被一些“不良出题者”冠以“奥数”的名称出现在各种习题集中。这样的事情有时是让人愤怒的,因为这些完全在误导学习者,会让人觉得数学就是一些偷奸耍滑的东西。
还有一些题目,的确是数学问题,但不是小学阶段的知识能解决的。有的问题要到中学甚至大学才可能解决。看到一些人被逼着“用小学方法”做高等数学题目,真是让人哭笑不得。
但今天,我们推荐了一道“小学数学题”倒是挺有趣,我们没有求证过这个是不是真的是小学某练习册上的题目,不过大家还是看题吧:
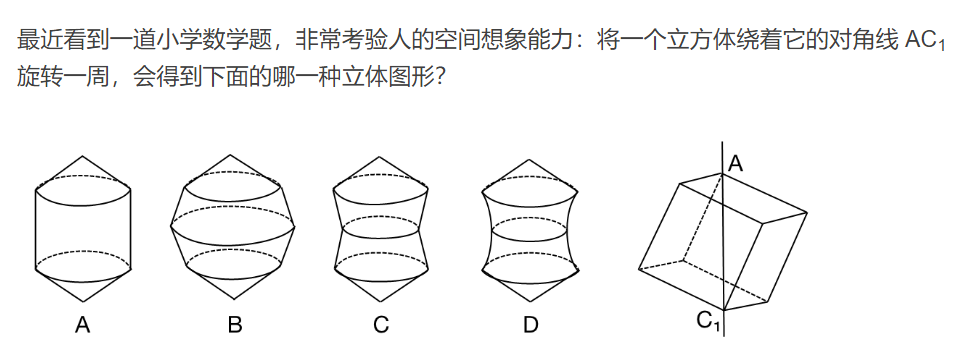
我们哆嗒数学网的小编认为,这个问题算是恰到好处,只是让定性的问问旋转体的结果是凹的还是凸的,直的还是弯的。没有超前的问具体形状以及面积体积的计算问题,用来考验小学生的感觉也是说的过去的。
为了求证问题的结果,我们坐起了实验。有点难度,还有点费眼,但是能看出大概应该是凹的。

但是,是直的还是弯的很难看出来。一些人直觉的猜了应该是直的,但一个人说的三个字,打破了这些人起初的直觉。
这三个字是:
直纹面!
看见上面三个字了吗?什么,没看见?那是因为我施用了魔法,你必须用特殊的操作解除魔法才能看见。
这个数学对象,在大学的时候也许还会重学,那时候会不会想起还提时代做这道题目的有趣经历呢?一个小学题目能提起兴趣,并在未来还可能回想起它,最酷的学习过程莫过于此。
那么问题的答案是什么呢?公众号中回复“旋转正方体”得到答案,不带引号哦!
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
原文作者,Bai Li,就读于多伦多大学计算机科学学院。
翻译作者,豆浆,哆嗒数学网翻译组成员。
校对,小米。

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Patrick Honner,美国杰出数学和科学教育总统奖得主。
翻译作者,radium ,哆嗒数学网翻译组成员。
校对,mathyrl。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
在刚开始理解什么是数学家和物理学家眼中抽象的对称结构,我们得先从熟悉的形状开始。
你得原谅数学家被魔群深深的勾住,一个如此巨大而神秘的代数对象吸引他们花费接近10年的时间去证明它存在。现在,三十年后,弦理论家们——也是正在研究所有的基本力和粒子如何通过在隐藏维度振动的微小的弦来解释的物理学家——发现魔群与物理学中的深刻思想有联系(研究出来的主要定理可以解释魔群的量子场论构造,事实上魔群是一种特殊弦论的对称群)。
这个元素个数的数量级达到10的53次方,并且同时让数学家和物理学家兴奋的集合是什么?在建立新的物理理论中搞清对称性的数学结构以及隐藏的对称性的过程中,像魔群这样的代数群的研究提供了线索。
群论在很多方面集中体现了数学的抽象性,但是它构成了一些我们的大部分类似于数学经验的基础。现在让我们研究对称性的基础以及阐明他们代数结构。
我们喜欢说一个事物具有对称性,但是它真正的含义是什么呢?直觉上讲,对于像镜像那样的事物,我们有对称的感觉。假设我们画一条垂直的线穿过正方形的中间。
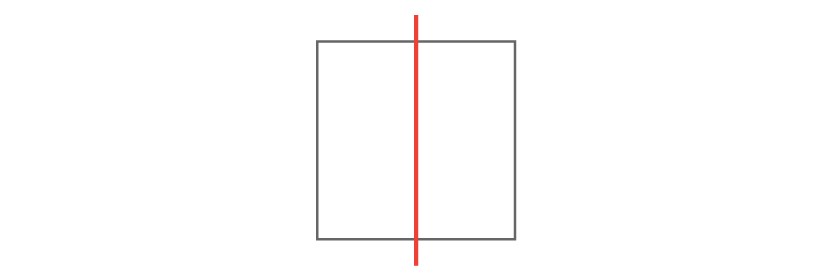
这条线将正方形分成两个相等的部分,这两部分互为对方的镜像。这个熟悉的例子被称为轴对称。但是这儿还有其他与镜像无关的对称类型。
例如,正方形还具有旋转对称性。
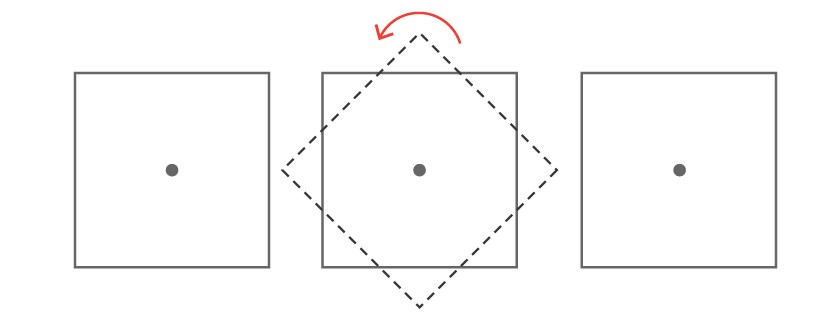
从这个例子中我们可以看见正方形关于它中心点(对角线的交点)逆时针旋转的过程。在旋转了90度(四分之一的翻转之后,它看起来和之前的一样。
我们定义一个对象变换是对称的,如果这个物体变换后与变换前的形状一样。上述旋转是正方形对称性的一种,而我们轴对称的例子可以作为第二种对称性。
让我们花一点时间来定义一些的术语。我们将称最初的对象为“原像”,而变换后的对象为“像”。我们将用术语“映射”去描述从一个对象(一个点,一个线段,一个正方形,等等)变换到另一个对象的过程。对称性要求变换不改变对象的大小或者形状。
一个变换如果满足这样的要求被称为“等距”,或者称作刚体运动。基本的等距变换是关于一条线反射,关于一个点旋转,以及沿着一个向量平移。
现在我们继续分析正方形的对称性。我们知道有一种对称性是“关于一条通过中心的垂线反射”;另外一种是“关于中心逆时针旋转90度”那么还有其他的吗?他们是什么?还有多少种?在数学中经常出现这样的情况,提前规定好的记号将让我们的分析更加容易。
首先,假设我告诉你我已经通过对称性变换好了正方形,下图是结果。

这样的结果应用了那种对称性?旋转?反射?当然这不可能精确地看出来运用了哪种对称的准则。为了帮助我们确认具体应用了哪对称性,让我们从标记原始正方形的顶点开始分析。
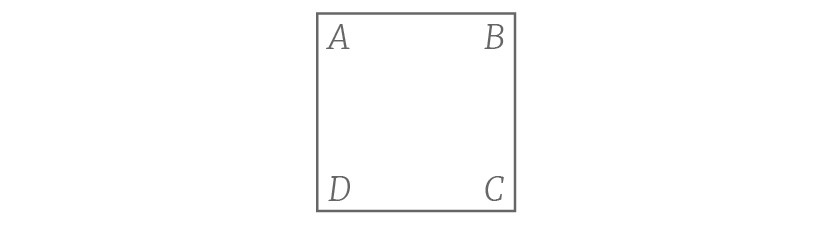
进一步,让我们规定不论何时我们描述原始正方形都用这样的标记:左上角为A,右上角为B,右下角为C,以及左下角为D。
好了,现在我们开始变换正方形,我们可以追踪标记是怎样移动的。例如,在关于一条过中心的垂线反射后,正方形变成了下面这样的形式:
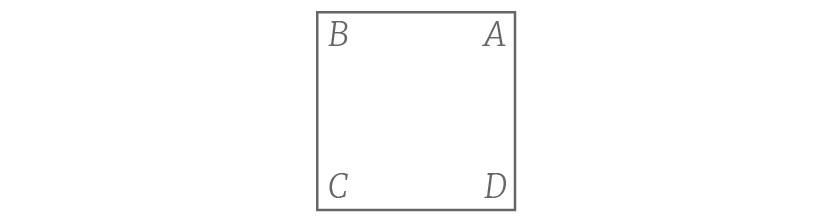
对比原始的标记,A现在在B的位置,而B在最初A的位置。类似的,C和D也交换了位置。将原始标签作为ABCD,我们将经过变换后新的标签记为BADC。
这样就清晰地揭示了,在这样的变换下,A被映射成了B,B被映射成了A,C被映射成了D,最后D被映射成了C。我们可以可视化记号是怎么变换的:

我们将一直记原始位置为ABCD,因此列表中的相对位置描述了每个原始顶点在变换下映射的位置。在另一个例子中,我们绕中心逆时针旋转90度可以标记为DABC,在这个变化中A被映射成D,B被映射成A,以此类推。
严格的来说,这仅仅描述了在一次变换中每一个顶点发生了什么。但事实证明,这足以描述整个正方形变换的情况。这是因为对称变换是等距的,因此维持了对象的大小和形状相等。
等距不能让尖角或顶点变平,因为那样将会变对象的形状。这意味着所有的角A,B,C,D都将映射成角。类似的,等距变换的性质保证了线段将映射成线段。
于是,一旦我们知道正方形的角往那边走了,相应的边也沿着相同的路线行走。换句话说,正方形边的像决定于对应端点的像。
这就意味着我们能完整的通过排列四个字母A、B、C和D具体说明正方形的一个对称。这本身是非常好的,但它同时也立即暗示着正方形对称的形式的数量有一个上界。正方形对称形式的种数不超过四个字母排列组合的种数。那么有多少种排列呢?
考虑用这些字母创造一个排列,你可以从这四个字母中的任意一个字母开始,但是一旦你选择了一个字母,那么对于第二个字母你就仅仅只有三种选择。一旦你选择了第二个字母,在第三个字母上你就只有两种选择,最后,对于第四个字母将你只有一种选择。一个基本的计数方式告诉我们有
4 × 3 × 2 × 1 (= 4!) = 24
4 ×3×2×1(=4!) = 24种可能的排列。因此,对于正方形这儿最多有24种对称方式。
事实上,正方形的对称形式远少于24种,一个简单的论据将告诉我们为什么。让我们回到原始图形。假设我们知道正方形的一个对称把A映射成B,那么C又如何呢?
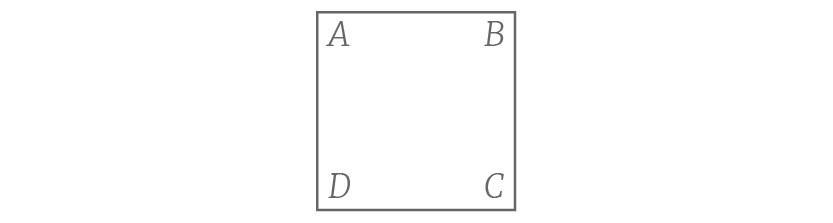
答案很明显,C只能被映射到D上去。A和C是正方形对角线的端点。因为等距不改变长度,A和C的距离必须和映射前的距离相等。如果A映射成了B,那么现在与A的距离等于对角线长度的唯一对应点D就是点C必须到达的地方。
这样就极大的减少了正方形对称性可能的数量。假定我们构造了一个对称,那么A点有多少种可能性?因为顶点必须对应到顶点上去,关于A的映射这儿仅有四种可能的情况。一旦我们选择了一种方式,那么A的对角线端点C的映射也只有一种方式。那么对于B就只有两种选择了,类似的方法我们可以知道D也只有一种选择。
notation:
最后,讨论正方形的对称性,我们真正需要考虑的只有两种情况:A点的选择方式(四种)以及B点的选择方式(2种)。这就意味着这儿仅仅只有4 × 2 = 8 种可能性。这儿用我们的记号列出了完整的清单:

现在我们无法保证所有的八种可能性都是正方形实际对称性。但是它是一个小的列表,所以我们可以逐一验证它。实际上他们都是合法的对称性:左边的四种是旋转对称性(旋转角度为0°,90°,180°,以及270°)右边的四种是轴对称(两个关于过中心的垂线和水平线对称,两个关于对角线对称)。
所以这八种变换都是对称性,我们已经确定了正方形最多有八种对称性,显然我们已经把它们全面找到了。但这真的就是全部的情况吗?
当我们发现一种自然的方式去组合对称方式,一个新的关系产生了:我们可以简单的应用他们在一系列变换在中(一种称为“复合”变换运算)因为应用对称性再次给了我们一个一样的正方形,你可以应用另一个对称性再次产生一个一样的正方形。
这就意味着如果你连续应用多个对称性,这些对称性的复合本身是也是正方形的对称性!我们可以通过上述八种的各种组合造成新的对称性。
但当我们试图这样做时一些有趣的事情发生了。假设我们逆时针旋转正方形90°然后让沿过中心的垂线反射,那么顶点会发生什么变化呢?
旋转让A变成D,然后经过反射到C,所以最终是A到C。B旋转到A,然后反射回到B,所以B映射到B。C旋转到B,然后反射到A,然后D旋转到C,然后反射回D。在我们采取的记号中,这些两次变换的复合可以被描述为:

但是这个对称都已经在我们的列表里面了!逆时针旋转90°后通过中心的垂线反射,实际上就是关于对角线BD做了一次反射。事实上,每一次上述八种对称性的组合本身也就是上述八种对称性之一。
现在我们已经在这些对称性集合中揭示了基础的代数内在结构。当我们通过组合两种对称性时,我们得到了另一种对称性,用一样的方式我们通过加法结合两个数字得到另一个数字。而恒等对称(旋转0°)在我们数字系统中表现为数字0.
而每一个对称性都可以被抵消,就像加三也可以加上-3来抵消:例如,正方形旋转90°可以被再旋转270°抵消。
这是群基本的代数属性,他们赋予群,就像正方形对称性的集合,具有类似于我们熟悉的数字系统的结构和规律性。但是对称性的群也展现了他们自己的复杂以及微妙的特征。
例如,我们关于正方形的对称群仅仅包含八个元素,与我们无限的数字系统形成了鲜明的对比。当我们能组合对称性在一定程度上相似于我们叠加数字,我们组合的顺序导致不同的结果,例如:3+4=4+3但是在旋转之后反射与在反射之后旋转结果却不同。
由简单的正方形对称性,我们已经对代数结构有了一种模糊的感觉,那么你是不是想知道数学家和弦理论学家研究的魔群深处的是什么了?
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
美国数学会评选的年度数学热门事件又来了,今年的晚了一些,大家来看看吧。

玛丽安・米尔扎哈尼,1977年5月3日——2017年7月14日

菲尔茨奖的唯一女性获奖者玛丽安・米尔札哈尼在今年7月14日去世了,年仅40岁。 米尔札哈尼是斯坦福大学的教授。她是一位极具原创性的数学工作者,对几何和动力系统领域作出了许多重大贡献。她的工作连接了几大数学方向——包括双曲几何、复分析、拓扑和动力学——反过来她的工作也深刻地影响了这些方向。世界各地的媒体都报告了她的生活和数学贡献。
《隐藏人物》,电影与数学家

电影《隐藏人物》在2016年12月发行前就得到了大量曝光。2017年1月AMS年度数学联合会上,本书作者 Margot Lee Shetterly和参与了美国航空工程的数学家 Christine Darden出席了该电影的发布会,现场座无虚席。2017年,电影明星在电视节目上谈论那些激励人心的女数学家故事,书本和电影引起了读书俱乐部的关注,学校组织学生去电影院,甚至还出现了一套以电影中的女性为主题的商标--这些都被媒体广泛报道。在2017年5月,美国航天局把其在弗吉尼亚州汉普敦Langley研究中心的一栋大楼以97岁女数学家凯瑟琳・强森的名字命名,用以表达她的敬意。
丹尼尔·罗思曼关于生物大灭绝的研究

麻省理工大学的丹尼尔·罗思曼教授在《科学进展》杂志上发表了名为《预测下一次生物大灭绝或全球灾难时间的数学公式》的论文。这无疑是一个沉重的话题。论文引起了广大媒体的关注。
数学与“杰利蝾螈”现象
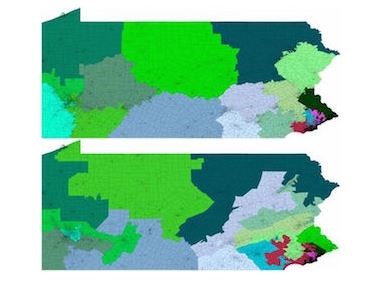
2017年夏天,数学家Moon Duchin在塔夫茨大学组织了一个度量几何与“杰利蝾螈”研究小组,旨在用新的数学工具分析和解决杰利蝾螈现象。(图:宾西法尼亚州一种可行的选区划分方案,它将整个州黄划分成为18个人口相等的选区。下图:宾州现行的选区划分。)
恩尼格玛密码机被拍卖

“一台罕见的纳粹二战期间使用的恩尼格玛密码机周二在拍卖会上以45,000欧元被一名匿名网上买家买走。”CNN报道。正如史密森尼学会指出,“这台恩尼格玛机是有史以来出镜最多的密码机。”这种机器在二战期间被德国军方改造用来加密信息,而盟军最终破译了这种密码——这是在2014年电影《模仿游戏》中讲述的故事。许多版本的恩尼格玛机都成为了收藏品,而这台被拍卖的恩尼格玛机格外引人注目,原因是它的主人在当初在跳蚤市场上只用100欧元买下了它。
维拉尼当选法国议员

43岁的数学家、菲尔茨奖得主赛得里克·维拉尼,在南巴黎的一次选举中赢得了69%的选票并成为了一名新的法国国民议员。在《科学》杂志的一次采访中,维拉尼说到,“我从未计划参与任何国家政治活动。但马克龙的政党对欧盟热情的支持,这在法国国家政党中是非常罕见的。它同时也反对过去的政治传统,即在选举中系统地攻击对手;相反地它倡导博爱、实用主义和进步。同时,他的政党也欢迎非政治家的专业人士。”
《数学杀伤性武器》

凯西·欧尼尔这本书的副标题是“大数据加剧了不平等并威胁了民主”。无论是在电台还是纸媒的采访中,欧尼尔都强调人们并不理解数学模型、算法以及打分系统如何在生活的方方面面影响了我们——大学录取、监狱系统、就业、保险、选举、棒球队招募、社交网格、金融系统和教育。在EdSurge的访谈中她谈到,“算法,说白了就是一种打分系统。只要你有了一个打分系统,你就可以钻系统的漏洞。漏洞钻得多了,系统就不再有效了。这就是现实。”
伊夫·梅耶尔获得2017阿贝尔奖

今天3月,挪威科学和文学会宣布伊夫·梅耶尔获得今年的阿贝尔奖,以表彰他“为小波分析的数学理论发展中做出的突出贡献。”阿贝尔奖是数学界中最有威望和慷慨的奖项之一。这则新闻被各大新闻和科学媒体报道,包括《自然》、《福布斯》、《卫报》、《法国商业报》、《爱尔兰时报》、《科学美国人》等等。
Urschel从橄榄球生涯退役成为一名职业数学家

作为一巴尔的摩乌鸦队的一名职业橄榄球运动员同时也是麻省理工一名数学研究生,Urschel因为他的双重份已经被媒体报道多年。2017年他决定在26岁的年纪从橄榄球生涯退役专攻数学。就在近日,一份报告揭露了橄榄球运动中广泛存在的运动员大脑损伤,但Urschel说他的决定更多地是为了更好地研究他的数学。
媒体达人尤金妮娅·郑

尤金妮娅·郑 把烘焙和高维范畴学结合在了一起。她对于数学及其与音乐、烘焙和日常生活联系的热情是充满感染力的——这是她为什么出现在许多的电视广播节目与出版物中。“数学是奇妙的,而我们也必须以一种奇妙的方式去对待它。”
π节

每年的π节(3月14日)都吸引了很多媒体的眼球。大量的故事和语音都在探讨它的历史、庆祝、相关的难题、游戏(想象呼拉圈和悠悠球),当然还有如何烹制派。学生和数学家们——今天还有美国航天局——都加入到这些向π致敬的有趣的活动中。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
根据中华人民共和国教育部官网消息,教育部学位与研究生教育发展中心公布了全国第四轮学科评估结果。第四轮学科评估于2016年4月启动,在95个一级学科范围内开展(不含军事学门类等16个学科),共有513个单位的7449个学科参评(比第三轮增长76%);全国高校具有博士学位授予权的学科有94%申请参评。

第四轮学科评估首次采用“分档”方式公布评估结果,不公布得分、不公布名次,不强调单位间精细分数差异和名次前后。采用按百分位进行分档的方式。根据“学科整体水平得分”的位次百分位,将前70%的学科分为9档公布:前2%(或前2名)为A+,2%~5%为A(不含2%,下同),5%~10%为A-,10%~20%为B+,20%~30%为B,30%~40%为B-,40%~50%为C+,50%~60%为C,60%~70%为C-。
数学学科中,全国具有“博士授权”的高校共76所,本次参评69所;部分具有“硕士授权”的高校也参加了评估;参评高校共计182所,进入榜单的共有129所。中国科学院大学的数学学科以科研单位参与了这次学科评估,得到“分档”为A+。所以,本次数学学科共有130个单位进入榜单,北京大学、复旦大学、山东大学、中国科学院大学四个单位获得了最高等级的A+。(注:评估结果相同的高校和单位排序不分先后,按代码排列)
另外我们哆嗒数学网的小编和之前公布的14所数学“双一流”名单做了对比。发现14所数学“双一流”高校中,此次评为A+的3所,评为A的5所,评为A-的3所,评为B+的3所。而评为A-以上(含)的高校或者单位中,有19所高校和单位中,有8所没有进入之前的数学“双一流”名单。这些学校包括浙江大学、武汉大学、南京大学等,通常认为的数学强校。

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Frank Calegari,芝加哥大学代数数论教授。
翻译作者,Math001,哆嗒数学网翻译组成员。
校对,donkeycn。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
五年前,Cathy O’Neil举出了一个有理有据的例子来说明(在五年前那个时间点上)为什么望月新一的声明(仍然)不应该视作ABC猜想的一个正式的证明。关于那篇帖子中讨论的数学的社会效应我这里不再做任何补充了,这里我只想向大家报告一下,在专业的数论学家眼里,现在是个什么情况。具体情况是什么?答案是,这简直是一场彻底的灾难。
这篇文章不讨论关于望月新一证明对与错的认识论上的哲学意义。举个极端的例子,如果望月新一把它的证明用古希腊线形文字刻在石板上,然后丢到马里亚纳海沟里,那么大家可能几乎不会怀疑,追问那证明是否存在过是一件毫不重要的事情。虽然说法极端,而现实情况和刚刚我的这个描述没太大差别。
我从某专家处(不便公开)得知,每一次望月新一的论文分析,结果报告都是让人不安的相似:大量声明的“显然的”结论,而这些结论依赖于巨量的未经验证过的理论。望月新一基于如下观点辩解:格罗滕迪克学派的数学产出也是遵循着相似的模式,而事实证明,这些产出已经成为现代数学的基石。这个典故大概是这样的:
笔者听过这样的故事:有一天,格罗滕迪克说,弄开核桃壳有两个办法。一个办法是,把核桃壳用坚果钳子使劲一口气夹烂。另外一个办法是,把它浸入有很多很多水的水缸里,泡啊,泡啊,使劲的泡啊,然后它自己就泡开了。格罗滕迪克的数学属于后者。
话虽如此,但拿望月新一和格罗滕迪克做对比并不好。是的,格罗滕迪克在20世纪60年代以革命性的方式“完全彻底”的重构了数学。但是,从法国高等研究所(IHES)生产的思想迅速传遍了世界,在巴黎大学、普林斯顿大学、莫斯科大学、哈佛大学、麻省理工学院、波恩大学,以及荷兰的一些大学等等,它们的讨论班已经展开了讨论。本质上,格罗滕迪克学派20世纪60年代的成功并不是用IHES产出的定理来衡量的,而是它产生的思想完全改变了这个学科(以及相关学科)里的每一个人思考代数几何的方式。

这不是对某人个人癖好的吐槽,也不是抱怨某些人不按“体制”的规则出牌。佩雷尔曼也拒绝按照学术圈的通常做法发论文,而是把他的论文简单直接地贴在arXiV上,就撒手离开了(补充:虽然佩雷尔曼从来没有正式提交论文,但他随后开办了巡回讲座,让其他专家接受自己)。但最终的结果是,在数学里,思想是永远的胜利者。人们可以读到佩雷尔曼的论文,能在文章中感知到他所有的思想(五年内,大量专家补充了原始证明里略过的完整细节,并陆续发表)。通常情况是,如果数学领域里有突破性发现,当其他数学家能利用这个新的思想证明其他领域的定理的时候,这个标志性的事件会引起学术成果爆炸式的增长。而且,通常这些事件并不能被理论的原创者预先感觉到。但这样的事情,并没有在ABC猜想的证明上发生。这样的现实下也就难怪人们对该证明如此强烈的质疑了。

事实是,现在这些论文似乎要被PRIMS(这是望月新一自己当主编的杂志,这事本身不是什么大问题,但依然有碍观瞻)接收了。被这样的杂志接收,并不能成为人们接受证明的理由,该证明的现有处境依然没有改变。如果说审稿程序有什么意义的话,那么它的意义就在于使人在一定程度上相信文章的正确性。(虽然有时候发表的文章也会有一些错误,但这些错误一般很快就能被比较专业的读者修正,或者有时候会发一个勘误表,当然也有很稀少的文章被撤回的现象)。也就是说,它迫使作者用清晰的文字,写出标准范式的语言,让专业人士能读懂文章(所以,除了其他特别的原因,审稿人不需要花费像作者需花费的那样多时间来审论文)。而在这件事情上,上面的功能就完全失效了,质疑会同时来自两个方面,审稿人对文章质量的评定,以及PRIMS编辑委员会对论文会以这样不可接受的,被广泛认为不透明方式发表的放任。那么,我们会进入一个荒唐可笑情形——ABC这个命题在京都是定理,但在其他地方都是猜想。(补充:一位日本读者向我指出,报纸并没有确定地说论文已经被接收,用的是“按计划论文会被PRIMS接收”诸如此类的措辞。这也不会改变本文的实质内容,这里还有论文不会以现有方式被接收的可能性,如果那样的话,我收回对PRIMS编辑委员会的批评。)
那么为什么这样的情况持续了那么长的时间?我想我能提出三点基本理由。第一,数学家通常是非常小心翼翼的(说个笑话——苏格兰的绵羊至少有一面看上去是黑色的)。因为数学家们不能指出望月新一证明的实质性错误,所以他们非常不愿意去声明这个证明有问题。于是,他们倾向于对任何一个关于错误的声明用极端谨慎(足够合理的谨慎)的态度。我们成长为数学家的历程中,如果听不懂别人的证明过程,通常会自我觉得很丢脸。第二,无论何时,数学家一旦做出一个特别的声明,大家开始的反应都会去看这位数学家之前的工作。这里,望月新一曾经在重要领域做出过成果,而且被很多认识他的人认为是一位智商很高的数学家。的确,一些默默无闻的人(比如最近的张益唐就是一个例子)声明自己证明了某个重要的结果,他的文章也会被认真对待,但是,如果类似不知名的人以望月新一的方式放出一个1000页的论文,他立马会被拒掉。最后一个理由,对比前两点,一些人愿意看到论文被公开,以及听到一切都很好的消息,而质疑者们也没有为理解望月新一的宇宙际几何的基础而做够功课。我没兴趣去揣测人们为什么这样做。但是,这种至少需要几百小时才能入门的理论要么是彻头彻尾的垃圾,要么是超越现有所有既有知识的体系。那么,不仅在数学上,而且在所有科学里都是前无古人的。

那么,事情会怎么发展?这里有很多种可能。一种可能是某位专家深度检查了论文,并能抽出论文的核心思想,然后对论文主干进行简化修改,让它更容易读懂。这是论文放出后梦想中的剧情发展,但一天一天地(一年一年地),这个可能性变得越来越小。但可能性仍然存在。与之相反的可能是,某位专家找到了一个严重的错误,用否定的方式来了结这个事情。第三种可能是,这个状态一直持续下去:没有“恩赐的一击”(编者注:人奄奄一息时给的最后一下,让其免于痛苦)来杀死证明,但是同时江湖上仍然在流传没人能领会论文中心思想的传说。(我想说论文是否被某个杂志接收和此毫无关系;这不是证明人们读过论文并认为论文没有问题的适当方式,必须有人能解释论文。)这种情况下,数学界会一直这样摇摆反复下去,可能会持续一年、十年或者一百年。直到有人最终证明了ABC猜想,然后回过头来对比,来看看那种证明的思想究竟是否真的一直在那里(大结局)。

陶哲轩在本文评论区的回复:

感谢博主的文章。我没有足够的专业知识去对望月新一的论文做一个直接的评价,但是对于你文章中提到张益唐及佩雷尔曼的工作却更加熟悉。它们之间一个显著的区别在于张益唐与佩雷尔曼的工作里有着较短的“方法验证”,即用他们的方法能很快得到相应领域里一些很有意思的不平凡的结论(或是发展出一些已有不平凡结论的新证明)。这些事情发生在论文发表之后,而不是之前。
在佩雷尔曼的工作中,第五页就已经给出了Ricci流的一个全新解释:它将Ricci流看成了梯度流,而这是一个看起来非常有前途的方法。在第七页,他就用该解释建立了一个关于Ricci流的非常精彩的定理。虽然这个定理离最后证明庞加莱猜想还有千里之遥,但是它本身就是一个新奇且有趣的结果。这也是为什么这个领域的专家迅速认定这篇文章中有很多“好东西”。
在张益唐54页的论文中,有很多对专家来说是标准性的内容(特别地,这篇文章沿袭了解析数论界的传统,将所有要用到的引理放在了文章的开头)。但是仅仅6页的引理陈列之后,张益唐就从中做出了不平凡的观测:只要能改进Bombieri-Vinogradov定理对光滑模的估计,我们就能证明素数间距离有限。(其实这个观测也被Motohashi和Pintz独立地导出,但其形式却无法被得心应手地运用在张益唐后面30多页的证明中)。这并不是张益唐论文中最深奥的部分,但是它却将原问题化为了一个看起来更容易处理的问题。与无数试图攻克像黎曼猜想等大问题的论文相比,它没有将原问题不断转化为看起来更复杂的问题(只有奇迹发生,才能将这些复杂的问题转化回一个简单的问题。)
从我了解的信息来看,对于望月新一所用的方法,最短的“方法验证”就是300多页ABC猜想的证明。如果能有一个更短的 “方法验证”(比如少于100页)就可以帮助人们消除对于这篇论文的怀疑。 如果说一个300多页的独立体系只能用来证明ABC猜想,且这个体系里不能衍生出任何证明其它结论的子方法,这将是一件非常邪门的事情。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
我必须坦诚交代我曾经对长数轴(long line)有着微微的敌意。但是当我看到Mike Lawler发的推文的时候,我觉得应该给再长数轴一个表达自己的机会。
Mike Lawler:
我对你的爱就像长数轴 —— 真情如往,仅更久长

就是说,长数轴是拓扑空间中的一张甜腻腻的情人节卡片。是否能找到它背后所有的意义,就是让我在数学里找寻爱情的表达,最幸福的事情莫过于此。
就像它名字表达的那样,长数轴真的很长,某种意义上说它比通常的实数轴“长”。我们能把通常的实数轴看成一串单位长度的区间一个接着一个拼接而成的直线。或者说明确一点,区间的个数与整数一样多。长数轴基本也一样,只不过区间的个数与实数一样多而已。
无论如何,如果这样的长数轴能作出来,应该是很赞的事情。但是,真相有点诡异,它会让我们撞入集合论错综复杂的旅程之中。集合论中关于无穷的很多断言曾经让数学家康托疯掉。我这里有言在先!
为了定义长数轴,我们得先讨论一下不同数量的无穷。当数学家们讨论集合的数量,或者说集合的基数,他们用的思想是一一对应:如果两个集合中,从第一集合里取出的每一个元素,都能从第二个集合取出一个元素与之配对,一个不多也一个不少,我们就说这两个集合有相同数量。换种说法,如果我们不想数手指的话,我们把两个拇指对起来,再把食指对起来,一直下去,直到把两只手的所有手指都对应了起来,于是我们知道,两只手的手指数量是相同的。

当我们把此方法用于无限集合的时候,奇怪的事情就会发生。虽然偶数只是整数的一部分,但是整数和偶数是一样多的。我们可以把整数写在左边一列,偶数写在右边一列,左边写n的地方,对应的右边写上2n。于是,我们找到了一个一一对应,这两个集合元素的数量是一样多的。然而对于有限集,你是找不到这样的一个一一对应的。
.
实数集合已经被证明是比整数多的,所以我们知道了至少有两种不同数量的无限集合。实际上,我们有从一个数量少一些元素的集合得到元素数量更多的集合的一般方法。所以,我们可以从整数的无穷开始不断生成无穷多个拥有元素数量越来越多的无穷集合。对于整数集合的无穷,我们把它叫做可数无穷。
这和我们要说的长数轴有什么关系?长数轴的确切定义其实不是用实数多个单位区间拼起来。而是把最小的不可数无穷(smallest uncountable infinite)多个区间拼在一起而组成的。
到了这里,我们将撞入连续统假设问题。连续统假设是说实数的无穷就等于最小的不可数的无穷。所以,如果实数的基数和最小的不可数的无穷相等,那么我先前长数轴的描述才是准确的。如果不是,实数无穷和整数无穷之间还有别的无穷的话,构造长数轴的区间数量应该用那个最小的不可数无穷替代。
那么,连续统假设是真的吗?好消息是,你认为它是真的是没问题的!1963年,Cohen证明了连续统假设和决定数学底层的策梅洛-弗兰克尔公理系统不矛盾。连续统假设不成立,也和策梅洛-弗兰克尔公理系统不矛盾(编者修正:这是一个误解,实际上连续统假设与策梅洛-弗兰克尔公理系统不矛盾在20世纪30年代就由哥德尔证明了,Cohen证明的只是后者,即,即便连续统假设不成立,也和策梅洛-弗兰克尔公理系统不矛盾)。就是说,连续统假设这个命题和数学的公理体系是独立的。你不可能用现有的数学公理证明或者否定连续统假设。一些人认为,这说明我们的数学底层还不完美,但我更倾向于支持另外一种说法——我们可以在一些没有矛盾公理体系之间自由切换。
我们是否决定接受连续统假设,取决于我们用长数轴能做多少事情。它有什么好处?和许多我喜爱的拓扑空间一样,长数轴可以用来打破你之前喜爱的数学用具——这是一个绝妙的反例。在这种情况下,长数轴告诉我们如果我们有太多好东西,也许并不一定是好事。最基本的,在长数轴上,我们不能建立微积分体系,因为它太长了。
至于原因,这牵涉到很艰深的技术手段,特别是你刚刚费尽脑汁思考完“最小的不可数无穷”的时候,我们来说说建立微积分体系要满足的三个条件也许更容易接受一些:第一,从局部看,它要和某个维数的欧氏空间相似;第二,它得是豪斯多夫的,就是说你可以让空间内的点分离开;第三,它还得是第二可数的,就是说它能从比较少(可数多)的集合中构建出来。长数轴不满足最后一条。虽然,你可能认为长数轴基本上和普通实数轴一样,但是它们其实有根本的不同,就是因为长数轴太长了。
“吾爱汝深深几许?今且听吾细数之…”(How do I love thee? Let me count the ways…),如果你心里总惦记长数轴的话,这勃朗宁夫人的诗句听起来也没那么动人了,“吾爱汝深深几许?勿可令吾细数之,犹如集构长数轴, 实为永世不可数!” 虽然诗意少了些,但貌似能更浪漫的表达你的感情!
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
这可能是10年来数学界最大的新闻:根据朝日新闻的报道,望月新一关于ABC猜想的证明,有可能发表,并予以确认。现在论文还在做最后的同行评议,如果没有问题,发表时间可能是明年1月份。
ABC猜想是数论领域最重要的猜想之一,于1985年提出。2012年8月,日本京都大学教授望月新一在其个人网站上贴出了该猜想的证明。该证明初版500多页,几经修正后达到600多页。由于望月新一的采用方法极其独到、创新性极强,文章又非常长,一时间数学界竟无人能理解其证明。当时有数学家认为,要理解望月新一的证明,可能需要数十年时间。

数论中,有很多著名问题都是ABC猜想的推论。比如我们列举的下面三个,曾经是数学界的神级问题,但在ABC猜想面前,就是简单的特例了:
莫德尔猜想: 该猜想于1984年被法尔廷斯证明。法尔廷斯因此获得1986年的菲尔兹奖。该奖被誉为“数学界的诺贝尔奖”,是数学研究的最高荣誉。
费马大定理:该猜想于1995年被英国数学界怀尔斯证明,轰动全球。初版证明300多页,精简后也有100多页。如果利用ABC猜想,将极大简化费马大定理证明。
比尔猜想:该猜想由比尔本人提出,并通过美国数学会悬赏100万美元求解。难度极高,用比尔猜想,你可以不超过5句话证明费马大定理。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
你即将搬家,所以你得在子事先没有过目的情况下租一个新的公寓。你网上也找了,电话也打了,终于相中了一个看上去不错的房子。但你到了你的新家的时候,总觉得有的地方…昏暗无比。实际上,房间所有地方都黑漆漆的,因为根本没电。你重新去翻看房屋出租的广告,的确,广告没有任何地方强调了房间就通电的,但你不会考虑你需要将这件事情当成一个问题去询问房东。
对于很多数学家来讲,豪斯多夫性质就像一个房间就应该通电一样自然。当然,你能构造一个不是豪斯多夫的空间,但你研究问题的时候,多少会认为,一个正在思考的空间是豪斯多夫的。在一个不是豪斯多夫的空间里做拓扑问题,那种感觉和在一个乌漆嘛黑的房间里乱撞没有区别。豪斯多夫性质是以德国数学家费利克斯·豪斯多夫的名字命名的。豪斯多夫性质描述的是数学空间中关于分离性的众多性质中的一个:空间中的点,它们之间的的分离程度到底有多大?一个拓扑空间是豪斯多夫的意思是,任意两个空间中不同的点,都能把它们分别放入两个不相交的开集里面。开集是拓扑空间中最基本最普遍的概念,你可以看看我们之前的文章,来了解一下为什么开集如此重要。
为了进一步了解豪斯多夫性质的重要性,我们来思考一些常见的空间,比如说实数轴。实数轴中的开集就是那些开区间(编者注:以及开区间并起来得到的并集),比如(0,1)。两个数轴上的点,无论他们距离有多近,他们之间总有一个距离区隔,所以我们能找到两个足够小的开区间,这两个开区间各自包含了一个点,并且这两个区间没有重叠的部分。
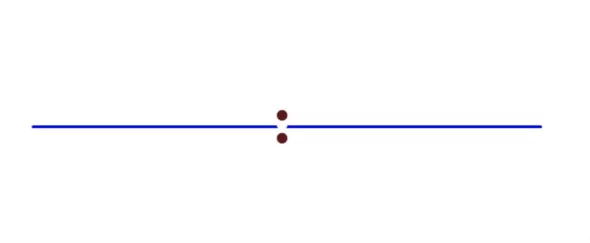
其他常见的空间——诸如二维欧氏平面、三维欧氏空间——同样具有这个性质。我们似乎有点难以想象一个空间没有这样的性质。这里我们来引出一个有两个原点的数轴——最简单的没有豪斯多夫性质的空间之一。
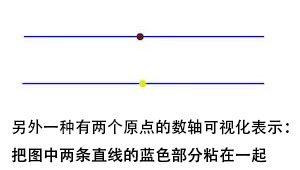
为了作出一个有两个原点的数轴,我们从作普通的两个数轴开始做工作。我们标记好两个普通数轴上的点,上面那条数轴的点为(x,0),下面那条上的点为(x,1)。现在,我们说我们把除了x=0以外的所有的(x,0),(x,1)这样的点都看成相同的点。而且我们设定,新的空间继承之前那两条普通数轴的通常拓扑,就是说,新空间的开集还是由那些开区间组成。
你可能无法接受我们把那样的两个点看成相同点的设置,但是思考拓扑问题的时候我们必须设定一些类似这样的规则。就像乔治·奥威尔的小说《一九八四》中设定“我们和东亚国的战争永无完结”(We have always been at war with Eastasia)一样,(1,0)和(1,1)在我们的设定中就是相同的点。
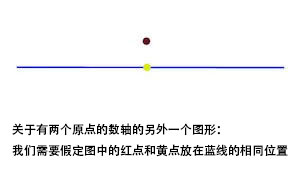
你能明白有两个原点的数轴不是豪斯多夫的原因吗?毫无疑问,定义中“除了x=0”引起了我们的注意。在上面的那条数轴中,每个包含(0,1)点的开区间,都和下面数轴中包含(0,1)的开区间有重叠的部分,这是因为两条普通数轴中,几乎所有的点都是相同的点。
虽然,我在本文中画了一些图形,但是仍然难以用准确的图形展示有两个原点的数轴。实际上,我们能在数学上证明我们不可能画出有两个原点的数轴,这也是豪斯多夫性质之所以重要的原因之一。一个没有豪斯多夫性质的空间是很难直观的展示的。但是一个空间如果满足豪斯多夫性质,那么我们就可以以某种适宜的方式将它纳入到某个欧氏空间,或者维数再高一些的空间中讨论。两个原点的数轴不能嵌入到任何一个欧氏空间来展示它的本质。于是,我们退而求其次,我们在纸上或者电脑屏幕上作图的时候,会省略掉一些点和线,希望读者能大致能理解。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
这是一套有日本数学会强力推荐数学科普书。原版在日本销售破40万。这回在人民邮电出版社放出《数学女孩3:哥德尔不安完备定理》中文版之际,我们再次推荐这套书的《数学女孩1》、《数学女孩2:费马大定理》、《数学女孩3:哥德尔不安完备定理》三本中文版合集套装。
《数学女孩1》: 讲述了很多数列和级数的知识!
《数学女孩2:费马大定理》:讲述了很多初等数论以及群环域等抽象代数的知识
《数学女孩3:哥德尔不完备定理》:讲述了很多数理逻辑、集合论、经典分析学的知识。

这是一个用数学串联所有线索的青春故事书。男主角人见人爱,虽然不是最强,但也聪明上进。三位女主角性格各异,在男主角的带领下,攻克一个又一个的数学问题。我们来看看书中的人物,如果你经常看日系漫画能领略其中风格。注意,我们这回推荐的是全文字的原版,而这里配图用的是它的漫画版本,注意区别。(漫画版本省略了很多数学部分,暂不推荐)
主要人物
“我”:

本作品的男主角,《数学女孩1》里面是高中一年级,后慢慢升入高二、高三,在家中是位独生子。非常喜欢数学,不满足与课本和课堂上学到的东西,经常找很多高深的数学课外读物和问题研究。在学校偶然认识了数学水平非常高的米尔嘉同学,开始男孩女孩之间关于数学的切磋历程。另外,经常在指导数学=学学习有困难的学妹泰朵拉,后来就当起了泰朵拉的私人家教,在图书馆、咖啡厅等地方非常耐心的解决数学问题。有时候会不经意的注意到身边女性的情感。也经常在家里教表妹尤里数学。
米尔嘉

女主角之一,男主角的同班同学,十分会弹钢琴。和其他人一样都是数学的爱好者。数学水平在男主角之上,男主角也经常找米尔嘉请教或者讨论数学。高中阶段已经能熟练的使用一些诸如群论、数论高等数学解决问题,方法简练却又不失严谨。人的外在表现比较高冷,但也时常表现出柔弱的一面。米尔嘉经常和男主角、泰朵拉、尤里一起讨论数学问题,高中毕业前收到美国大学的邀请出国留学。
泰朵拉

比男主角小一届的学妹,在初中时和男主角同校并且对他有好感,后来又念了同一所高中。数学较弱,遇到排山倒海般的算式或是学校老师解释不清楚的观念时会受不了。受到了男主角的指导而学会一有问题时就要积极发问,确认自己懂了,整理好思绪后才会继续前进。个性有点天然呆。在男主角指导下,数学进入了全年级前10%。
尤里

男主角的表妹,在家中是独生女,小男主角三岁,会称呼男主角为“哥哥”。由于自家和男主角的家相当的近,便经常到他家中作客,喜欢在男主角的房间看书,常出题给男主角。把自己自认为“猫女”,会在撒娇时发出“喵”的声音当作语末助词。
其他人物
盈盈

非常擅长钢琴,经常和米尔嘉一起练习钢琴。在书中戏份不多,没怎么进入主角们的数学世界。
村木老师

一位古怪的数学老师,喜欢男主角和米尔嘉。常出一些和课程内容无关,但是很有趣、且值得探讨的题目,也就是“研究课题”,并习惯写在卡片上给主角们带回去思考。不会硬性要求要回答,但是主角们还是习惯会提交报告给老师。
都宫

擅长运动,数学成绩全年级第一,但是并没有实际参与主角们的讨论、活动。前期,偶尔出现。
瑞谷老师

图书室的女性管理员,时间一到就会宣布闭校、放学时间到了。
“我”的妈妈
很喜欢尤里来家里作客,每次到来,都会用上好的料理招待。和所有的日系妈妈一样,每当气氛尴尬的时候,她就会出来说:“喝杯茶吃点东西再聊吧!”
当然,最后的结局往往都是——大圆满!下面是《数学女孩3》的结局。


关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Evelyn Lamb,数学及科学普及自由作家。
翻译作者,Jessie仪,哆嗒数学网翻译组成员。
校对,donkeycn。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
数学总是将可定向亏格比作一种甜点,即拓扑例子里最美味的那种。

.
啊,这个简单的环面是拓扑学家们最初的朋友,它也展示了理论与实践的差距。环面有很多特性而且在数学的各个领域都会出现。第一,他有一种拓扑的特性。拓扑学并不关心你看它的具体形状像什么,它只关心大体上的特征。具体来讲,它关心物体在没被撕裂或粘合的情况下,那不论是被拉伸还是被压缩都不改变的方面。在拓扑世界中,环面是一种带着一个洞的二维空间,或者说是一个曲面。(更高大上说来,它是一个亏格为一的可定向曲面。)急于将他们自己与更吸引人的烘焙学科联系在一起的拓扑学家们将环面描述为甜甜圈,虽然在某种无聊的精确角度来看,它其实仅仅是甜甜圈表层的糖浆涂层。(甜甜圈的面包胚是一种叫做实心环面的三维空间。)
.
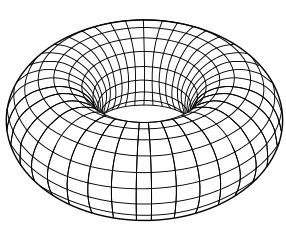
我们经常以一个被完美充起的甜甜圈来代表环面,但是拓扑学家们偏向于以一种更抽象的方式来描绘它。在下面这张图片中,我们将它画成带着几个标记的长方形,这些标记叫做特征点。
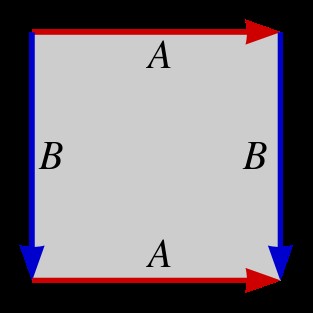
图中上面带“A”的箭头所对应的边和下面带“A”的箭头所对应的边将会被粘合在一起,左面带“B”的箭头所对应的边和右面带“B”的箭头所对应的边将会被粘合在一起。
正如在经典游戏小行星(Asteroids)中,当你从长方形上方的边走出长方形时,你会在下方的边上再次出现;当你穿过长方形的右边时,你会在左边重新现身。这幅图尽管不如甜甜圈那么令人垂涎,但仍然向我们展示了环面所有的重要拓扑性质。
这幅平面的长方形图片也良好承担了通向另一个环面生命的责任:作为几何物体的生命。不同于拓扑学,几何学确实关注实际的形状与距离。一个“环肥”的环面和一个“燕瘦”的环面尽管在拓扑概念上相同,但就几何概念而言,是不一样的。
几何学家们之所以关注这张环面的长方形表示,是因为本质上这是一个平坦的有限平面,就像一个无限平面。如果你曾不愉快地意识到格陵兰岛其实只有非洲大陆面积的7%,而不是和非洲面积一样大,你潜意识里就已经明白了一个事实:球面不可能被保持距离的展到平面上。这是因为球面曲率为正的,而平面是平的(注:曲率为0)。同样存在一种负曲率的曲面,他们也不可能被毫不扭曲地扯平。这个长方形图片展示了“环面是平的”这个事实。那么,这可就太好了,因为这样的话,它就能成为一个三维空间中实实在在存在平坦曲面,从而我们能直接观察到它;而不只是把它画在纸上然后还需要运用我们的想象力去想象。我们可以试着通过操作那些长方形上的被标记的那些边来这么做。我们从一个长方形开始。

第一次粘合把一张平坦的白纸变成了一个圆柱体。

第二次粘合将圆柱两端连在了一起。

实际上操作起来还是有些困难的。得到这个环面并不像计划那么顺利。这是一个理论与现实的不和谐碰撞。

当它们进入现实世界,当一个数学对象进入现实世界后,一般来讲,它很难再保持完美。我们没法画出一个严格意义圆,而且那个我们用来画图的曲面,也并非一个严格意义下的二维对象。但专心致志与优质圆规可以让我们画出与我们目标足够接近的圆。然而,环面,那可就是个噩梦了。
所以,我们到底能不能把环面放进三维空间中而不改变任何距离?
我们当然能!但是这没有你所希望的那么容易。

一个选项是,我们放弃那个完美平滑的曲面。在平面上,那个长方形没有任何折痕,但如果我们搞出一些来,我们就有处下手了。这么干的方法有很多。几年前我就做了一个。
数学3D打印的大魔法师Henry Segerman有一个脊被接合在一起的优秀例子。

要是我还不满足呢?要是我想把这些不和谐不雅观的折痕除掉呢?嗯,我们也能这么干!不过这就有点复杂了。在2012年,Vincent Borelli, Saïd Jabrane, Francis Lazarus, Boris Thibert, 以及Damien Rohmer发表了第一批没有任何尖角的三维空间平坦环面的图片。他们写道:“这些图片展露了一个令人意想不到的对象,处于分形和普通曲面的中间:一个平滑的分形。”换句话说,他们将分形的无限特质与一个平滑过程结合到了一起,从而避免了尖角的出现。

最后,这个“平坦的”环面看起来一点也不平坦,但它成功体现了它的字面意思。所有的距离都与他们还在那个平面上的长方形时完全一样。(若想进一步了解这种平滑分形的环面,请参见https://www.youtube.com/watch?v=5qu3WETuf6c)
环面还有很多其他变体:在拓扑学中,它是乘积空间中的最初例子之一,也是在运用 Seifert-van Kampen定理的第一次有用尝试。在动力学中,它是学生们最初碰到并能在其上“打台球”的平移曲面之一。在我所研究的领域,Teichmüller 理论,这是少有的几个简单到你真正可以理解并进行计算其Teichmuller空间的空间之一。一般来说,环面看上去就是那种每当遇到了新观点时,值得用千百种定理来描述的例子。带着感恩节季的精神,就让我们花点时间来感谢环面,因为它是让我们无论在二维几何还是拓扑学中都可以染指的好例子。(毕竟,数学总是比一个可定向亏格为一的甜点要好。)
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
2018“科学突破奖”颁奖典礼2017年12月3日在位于旧金山的美国国家航空航天局(NASA)阿姆斯研究中心揭晓,旨在表彰生命科学、基础物理及数学领域最杰出的成就的研究人员单项奖金为300万美元,此次共颁发2200万美元奖金,从奖金来看的确为科学界第一巨奖。
本次数学奖由来自美国犹他大学的克里斯多夫·哈康(Christopher Hacon)和来自美国加州大学圣地亚哥分校的詹姆斯·麦克南(James McKernan),一起获奖,分享300万美元奖金。另外,还有4位数学家获得3个数学新视野奖。中国数学家,恽之玮和张伟分享了其中一个奖项,该项奖金10万美元。值得一提的是,两位中国数学家都毕业于北京大学——北大的数学简直太厉害了。
“科学突破奖”有着“科技界的奥斯卡奖”之称。之所以有这个称谓除了高额的足以吸引任何媒体眼球的奖金意外,还有一个原因便是它的颁奖典礼星光璀璨,聚集了科学、技术、娱乐等各界明星——之所以这样颁奖,我们能从该奖项赞助人之一的尤里·米纳尔的话中,探知一二:“我小时候,占领各个版面头条的都是科学家,而现在情况全变了。我认为,这些改变世界的科学家们,完全有理由被世人知晓”。
以前,我们只是报道一下获奖情况,很少有人介绍颁奖典礼的具体过程。这回,我们随小编一道,以2018颁奖盛典为模板,让大家来看看,这个“科技界的奥斯卡奖”的颁奖盛典。
当然,我们哆嗒数学网作为一个身在中国的数学普及公众号,会更多的聚焦盛典的中国元素和数学内容。
先说说这个奖项的资助人。资助人可都是互联网和科技界的大咖,除了刚刚说的尤里·米纳尔,还有谷歌的联合创始人谢尔盖·布林、脸书创始人的扎克伯格、23andMe联合创始人安妮·沃西基。当然,还有中国人都知道的阿里巴巴的马云。以及刚刚不久前加入成为赞助人的,另外一个大家耳熟能详的中国互联网巨神腾讯公司创始人马化腾。
既然是奥斯卡奖,当然不会缺少走红毯的环节啦。让所有杰出的科学家享受巨星般的待遇是这个盛典的目的之一。下面就是恽之玮和张伟出现在红毯上的照片。

典礼开始前,会有一个比较热血的开场白,这几年这个念白似乎一直没变过:
“今晚在美国硅谷一号机库和航空航天局阿姆斯研究中心现场。科学界、技术界和好莱坞最璀璨的明星们齐聚一堂。他们将把超过2500万美元的奖金颁发给在生命科学、数学以及物理学领域的有杰出成就的人士。——这就是“科学突破奖”,他们是改变世界的科学家!”
念白完毕,LOGO登场。

当然,每一次颁奖典礼都会有一个主持人,这一次的主持人是,很多人眼中的“上帝”——摩根·弗里曼。

在台下,我们也发现了曾在中国红极一时的超级“网红”——“奶茶妹妹”章泽天。现在她是京东创始人刘强东的夫人。

当然,任何庆典都不会缺少音乐。这回的音乐表演是由超级巨星大提琴手兼演员欧阳娜娜(大会背景旁白就是这样介绍的)和多次获得格莱美奖提名的嘻哈说唱超级巨星歌手维兹·卡利法共同演出。大提琴和说唱的结合也蛮有特色的。

伴奏中,还有中国鼓。

表演结束后,主持人弗里曼再次感谢了欧阳娜娜,并向来宾们强调,2000年出生的欧阳娜娜只有17岁。这引来全场的欢迎,欧阳娜娜也起身向周围表达谢意。

庆典上,主持人弗里曼从生命科学家和其他人们一直在和各种疾病做斗争,引出了两段悲伤的故事。其中一段是关于数学家米尔扎哈尼的。这位当今唯一一位获得过菲尔兹奖的女性今年因为乳腺癌去世,享年40岁。而庆典中展示的米尔扎哈尼2014年从时任韩国总统,同样是女性的朴槿惠手中接过菲尔兹奖的照片,让人唏嘘不已,感慨世事无常。

2018“科学突破奖”的数学奖的颁奖嘉宾有两位。一位是曾经红遍全美的NFL橄榄球球员、麻省理工数学博士约翰·尤索,另外一位是DeepMind创始人戴密斯·哈萨比斯。DeepMind公司制作出的围棋人工智能软件AlphaGo,打败了人类最强棋手的。

颁奖之前当然是获奖者的VCR,视频大概1分50秒,视频中哈康称自己是一个“Slave Driver”,好吧,这是一个俚语,我们强行翻译成了“大恶人”。
两位获奖人领奖。获奖感言是由哈康一个人说的。他表达了希望更多的研究人员进入他们所在领域的意思。他还强调他们会乐于和所有进入该领域的人分享最深刻的研究成果。

最后全体获奖人员上台,大结局。

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Evelyn Lamb,数学及科学普及自由作家。
翻译作者,金星光,哆嗒数学网翻译组成员。
校对,mathyrl。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
遇见莫比乌斯带——拓扑世界中最具有“讲故事”潜力的拓扑结构。
如果你和数学家戴在一起或者去参加数学拓展项目,你很有可能会遇到莫比乌斯带。它在数学世界中是一个很特别的存在,原因在于它很容易被制作,娱乐性很强并且隐藏着一些令人吃惊的数学秘密。
你可以在自己舒适的家里,仅仅用一条纸带或者意大利面团就可以做一个莫比乌斯带。将纸带(或面团拉成条状后)一端固定,另一端旋转半周后,将两端粘到一起就可以得到一个莫比乌斯带。它看起来很像一个圆柱体,但还是有些不一样的。如果碰巧你是一个编织手的话,或许能够制作一个可以穿戴的莫比乌斯带。

我们通常使用莫比乌斯带来说明拓扑学中的可定向性。可定向性是你所熟知的但却很难被定义概念之一。我不记得有多少次我盯着我的教科书里对于“定向”的定义:“一个对于局部定向的连续选择。”我觉得这个解释毫无用处。为什么这个词的定义中还会包含这个词。
还有一个更直观的方式去理解可定向性,至少对于一个在三维空间中的二维的物体来说,空间是可定向的。如果你可以选择“向里”和“向外”或者“向上”和“向下”,来定义二维空间表面每一点的方向,并且这个方向具有一致性。你该不会用“从上到下”来定义一个相同点的方向吧?
或许弄清楚莫比乌斯带最直观的方式是将一个球体、一个圆柱体和一个莫比乌斯带一起把玩。如果你拿着一个球体,在北极点处你可以宣称此点方向“向外”,指向为竖直向上。当你在球面上移动该点时,“向外”的方向仍然指向球体外部。相比之下,试着在莫比乌斯带上任意选择具有“向上”或者“向下”的点。当你沿着莫比乌斯带滑动时,最终回到最开始所选择的点,方向已经由“向上”变成“向下”了。尽管你用一张具有正反面的普通纸制作成莫比乌斯带,但此时已经失去了正反面。你可以通过直线移动,从纸的正面到背面,而不是把纸翻转过来。
在莫比乌斯带中蕴含着很多数学中的奇妙现象。一个经典的做法是将莫比乌斯带沿中间剪断,看看你能得到些什么。如果将莫比乌斯带沿三等分线剪开呢?如果你将莫比乌斯带再多旋转几个半周、结果又会怎么样呢?比起在博客上阅读,不如自己在家里验证会更有意思。
我最近才了解到到的有关莫比乌斯带的特性是六色定理。你可能听说过四色定理:任何一张地图都可以用四种不同的颜色将其涂满,并且相邻的国家颜色不同。这个定理并没有它所陈述的那样正确。我们需要指定这张地图是在球面或平面上。准确来讲,不同的表面上有不同的地图颜色定理,而对于莫比乌斯带,它是六色地图定理。
要使这个定理得到验证,首先要记住莫比乌斯带是像任何好的数学对象一样,是一个理想化的存在,它并不存在于我们混乱的现实世界中。它是二维的,不是像真实的纸张那样是三维的,因为不存在任何的厚度将它前后面分开。为了将这一观点形象化,你可以用一张透明的纸制作一个莫比乌斯带。这样,当你绘制你的地图时,你就不能在任何一点上把纸的两侧染成不同的颜色(莫比乌斯带是二维的)。如果你在一张纸上绘制地图,然后再把它折成一个莫比乌斯带,那么平面上的四色定理将会起作用。

在这里我有一张需要用六种颜色涂满的莫比乌斯带的图片。在你的电脑屏幕上可能很难看出来,最好的方式是自己在家里制作一个吧,而不是听我在这里讲!
莫比乌斯带也同样吸引着艺术家。你可以制作或者购买印有莫比乌斯带图案的围巾、吊坠和戒指,你甚至可以演奏有关莫比乌斯带的音乐。它讲故事的潜力也是很强大的:你沿着某个东西转了一圈,回到起始的地方但迷失了方向。向上变成向下,向里变成向外。或许以莫比乌斯带作为故事的创作背景,最赞的就是Vi Hart创作的感人故事啦, Wind 和 Mr. Ug,两个“似乎”永远不可能相见的朋友。
(https://www.wimp.com/mobius-story-wind-and-mr-ug/ 这是这个故事的链接视频,没有字幕但很容易听懂。整个创作是在一个莫比乌斯带上完成的,先是讲了 Wind and Mr. Ug的故事,后来是Wind 与她的a little pet dog的故事,但后来发生了地震,至于这个故事的结局还需要大家自己去制作一个莫比乌斯带去探寻哈~)
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Evelyn Lamb,数学及科学普及自由作家。
翻译作者,donkeycn,哆嗒数学网翻译组成员。
校对,小米。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
拓扑学所关注的是压缩和拉伸,而不是距离。然而无限耳环展示了拓扑学和几何学之间微妙的关系。
拓扑学有时被称为是戴上啤酒眼之后看到的几何或者是没戴眼镜看到的几何。几何学研究各种形状:它们是如何位于空间中的,它们是如何与自己以及彼此之间相互作用的。做几何通常需要用某种方式来测量距离。而另一方面,在拓扑学中,你可以毫无顾忌地拉伸或压缩;所以,在一个拓扑空间中,任意两点之间的精确距离不是本质问题。然而有时候不经意间,几何就会出现。一个数学对象的几何性质会影响其拓扑性质。
无限耳环,有时也被称为夏威夷耳环,是我在拓扑中最喜欢的例子之一,因为它展示了几何学和拓扑学之间精妙的关系。
为了构造无限耳环,你可以从一个二维欧氏平面开始:先添加一个以(1,0)为圆心,1为半径的圆;再添加一个以(1/2,0) 为圆心,1/2为半径的圆;再添加一个以(1/3,0) 为圆心,1/3为半径的圆。继续这样做下去:无限耳环由所有以(1/n,0) 为圆心,1/n为半径的圆构成,其中n取遍所有正整数。
最终,你会得到一堆嵌套着的圆,并且它们恰好只有一个公共点(0,0)。当然事情并未到此结束。思考一下无限耳环它不是什么,这是很有教益的。例如,它不同于过同一个公共点的无穷可数多个相同大小的圆组合起来(我们称之为由可数多个圆构成的楔或花束)。这一事实可能会令人惊讶,因为毕竟,我们可以用不同的压缩比例来压缩那些圆,然后再把压缩后的那些圆压到同一平面内;或者也可以从另一个方向进行转换:通过吹胀无限耳环中的那些小圆至相同大小。尽管这些转换都很平淡无奇,但这两个空间并不完全是拓扑等价的。
圆本身也是一个拓扑空间,当我们谈论无限个圆时,我们并不要求它们位于任何特定的空间中。然而无限耳环却位于一个平面内,这就影响到了它的拓扑性质。我们无法将由可数多个相同大小的圆构成的花束形状放入一个平面内,因为这些圆将以我们不希望的方式产生重叠。
证明两个空间在拓扑意义下相同是很困难的,但只要有一个拓扑性质不同就能证明它们是不同的。证明无限耳环不同于由可数多个圆构成的花束的最简单的方法是:放大某些特殊的点的周围,然后看看你能得到什么。如果两个空间是拓扑等价的,那么当你在两者对应的点附件同时放大时,你会看到拓扑等价的东西。这两个空间最特殊的点就是所有的圆的公共点,即楔点。如果我们看一看这个点周围的一个小区域,我们就会发现我们想要找的差异。
在圆构成的花束中,楔点的一个小邻域由每个圆上一点的小邻域构成。它就像一把意大利面条。(“很多”根意大利面条。)
无限耳环上的点(0,0)周围的一个小的圆邻域是欧氏平面的一个小圆。它具有某个有限的半径,且该半径大于耳环内的某些圆的半径。事实上,它比其中的无数多个圆的半径都大。所以该小圆包含了耳环内无穷多个圆。也用面食来做比喻的话,它就是有限多根条状的面以及无限多根(很小的)圈状的面。
无限耳环和由圆构成的花束之间的区别还可以以其它复杂而宜人的方式表现出来,但我想我会把它们留待以后。现在,我打算再考虑另一个异于无限耳环的空间,而这个空间也是位于一个平面内的。
如果我们是向外构造圆,而不是向内,即它们具有整数半径1, 2, 3,等等(也许我们应该称它为更大的无限耳环)。我们得到了另一个与无限耳环完全不同的空间。有几个拓扑性质可以区分这两个空间。最容易看到的是:无限耳环是有界的而更大的无限耳环不是。
这两个无限耳环之间的另一个区别是:其中一个空间是闭的,而另一个不是。平面上的闭集有几个等价的定义。其中之一是:任何与集合中的点非常接近的点都在该集合中。更大的无限耳环不包含y轴上除(0,0)外的其它点,然而随着耳环中的圆越来越大,它们看起来越来越像一条直线,所以它们越来越接近y轴。当我们取遍整个空间的无限个圆时,y轴上的每个点都非常接近更大的无限耳环上的点,但它们每一个都不在更大的无限耳环上。
另一方面,较小的无限耳环就不存在这个问题。半径为1的圆是所有圆中最大的,所以该圆限制了y轴与所有圆接近的程度。
我花了一段时间来接受这样一个事实:无限耳环与圆构成的花束以及更大的无限耳环真的是如此不同,一个空间的几何性质真的可以对拓扑性质产生这样的影响。我想,在学习拓扑的人中,不是仅有我感觉自己只是在相信别人说过的话,却没有办法把它们真正内化。但在那种时候,我会用约翰·冯·诺依曼的一句话来安慰自己:“没人能理解数学,你只能是熟中生巧而已。”
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Evelyn Lamb,数学及科学普及自由作家。
翻译作者,独行者,哆嗒数学网翻译组成员。
校对,donkeycn。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
铺满空间的曲线,一张在空间维度中具有跨越维数的谜图,他有着惊人的现实应用。
停下来看看这个独特的现象吧。想看一条能铺满空间的曲线的图像?看吧,就在下面!

啊,你一定会认为我是个逗比吧!一条可以铺满空间的曲线就好像说:一条线可以乱画,然后弯折便能铺满一个2维的区域,在这个例子中便是一个正方形。(同样地3维,4维空间的曲线也是如此,一条线可以铺满你所给的空间!)
铺满空间的曲线在他们的完整形态上并没有什么特别的特征。你可以从黑色实心正方形中学到什么?相反地,就像其他的分形,我们通常可以认为铺满空间的曲线可以是一个有限步的构造的无限版本。
有多种利用迭代来构造铺满空间的曲线的方法,这里是其中一种的动画版本(其实是希尔伯特曲线)。

在每一步,线中的每一段都被一个四段的折线所替换。这个过程中的每一条曲线都不能铺满整个空间,然而如果我们想象一下,这个过程要是可以一直持续下去,那么最终我们得到的那个无限版本就可以铺满整个空间了。
铺满空间的曲线挑战了我对维度的直觉。一条铺满空间的曲线就是一条直线的像,这一普通的一维对象,却可以铺满整个平面,这一普通的二维对象。这感觉就像是一个规规矩矩的函数,就不应该把一个一维的东西“映成”一个二维的东西一维便是一维,二维就是二维,两者毫不相干。不过还好,它只存在于无穷的情况,只是仍然有些让人不安。
(如果你正在学拓扑学课程,你可能会非常紧张。线和平面是拓扑上是不等价的,但是一条铺满空间的曲线却是一个连续的函数,他将线“映成”平面。这是怎么回事呢?难道,数学根基的错误被我们发现了?)
很难想象这种如此抽象化的弯曲程度近乎无限的线会在现实世界中有什么联系。但是事实上,充满空间的曲线让一维空间“映成”二维甚至多维空间的方法在数据处理中有许多现实应用。在这个非常奇妙的视频中,Grant Sanderson解释了一种能充满空间的曲线,希尔伯特曲线,是如何帮助我们寻找到一种最优的途径将一个图像的二维可视化数据转为一维声音数据。(B站传送门:https://www.bilibili.com/video/av4201747/index_2.html#page=1)
如果你想在自己的电脑里实现,这里有许多方法生成你自己铺满的空间曲线。如果你想投机取巧的话,只需要涂满一些方块。如果你对如何实现使用迭代方法来构造铺满空间的曲线,你可以遵循Vi Hart的方法来画龙形曲线,而Andrea Hawksley(她的灵感来源于Kyle Calderhead)将帮助你编织一条属于你自己的以希尔伯特曲线为图案的毛毯。
对于我而言,我在一本以数学为主题的绘本《Patterns of the Universe》中寻找到了属于我自己的铺满空间的曲线的奥妙。在他们的书里,有两页画了铺满空间的曲线。一条是在封面上显示出来的,而另一张则在下面,是用线将点连起来的图形。
在这个星期的前半部分,我一直驳斥着一些人对数学教育的错误观点,而此时给一条舞动的蛇上上色就能使我的心归于平静。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Evelyn Lamb,数学及科学普及自由作家。
翻译作者,radium,哆嗒数学网翻译组成员。
校对,sanshi。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
在拓扑空间中,拓扑学家的正弦曲线的经典在于它连通但非道路连通,即你可以看到他的终点线,但你不能从这里跑到那里。

分析和拓扑的学生初看这个集合有四个基本的性质:开区间、闭区间、紧的以及连通性。在前面的这些性质中似乎连通性是最简单的。
连通这个词语的解释很好理解,但在数学中要严格地定义却出奇的困难。拓扑学家的正弦曲线就是众多例子中的一个,这个例子可以明确的说明连通的含义。
在通常词典里,我们通常认为连通是两个物体之间的性质:A和B如果以某种方式重叠或者你可以从A连到B那么我们说A和B是连通的。在数学里面连通性是一个集合的性质。那么我们如何让自然语言的思想数学化并应用它?一个似乎很理所当然的定义是,如果你可以从集合中的一点到集合中的任意一点那么我们称之为连通。但是如果是联排公寓又如何呢?
在联排公寓中,你可以从一个房间到同一单元的另一个房间,但如果你不离开联排公寓你就不能从一个单元到另一个单元。那么联排公寓楼连通么?我想应该是连通的。所以这不是连通的正确定义。能够在集合中从任意一点到另一点是一个非常有用的数学性质,但是这个性质太强了。数学家称这样的空间为道路连通,稍后我们会仔细讲讲它。
连通性是一个很微妙的东西,我们再次尝试着定义如下:一个集合X是连通的,如果你不能粘贴一子集在某个非空子集A中,而剩余的部分在非空子集B中,以至于A、B不相交。这里有一个小问题:这样的定义可能会完全失效,因为这会让太多的空间分裂。我们可以将所有实数集分裂成这样的集合:大于等于0,小于0。它们不相交,因此以我们的定义实数轴是不连通的。很明显通常的实数轴因该是连通的但是这样的定义让它不连通了,所以,这就错了。
问题在哪里呢?我们将分界点包含在一个集合中而没在另一个集合中。如果我们让两个集合同时包含分界点,集合将会相交;如果两个集合都不包含分界点,集合将不会相交,但是这两个集合也就不能覆盖实轴上所有的点。“正确”的答案是从两个区间中排除端点。 区间不包含它的端点我们称为开的。所以我们说集合X是连通的,如果你不能做到粘贴某一子集在非空开子集A中,而剩余的部分在非空开子集B中,且A、B不相交。
这个定义不仅仅在一维集合中成立;我们也可以在更高维定义开集。基本上,一个集合是开集如果这个集合中没有任何一个点位于边界上,或者等价的定义,如果集合中每一个点都存在完全包含在集合中的一个小邻域那么这个集合为开集。
下面是拓扑学家的正弦曲线的一部分,注意到图形的左边部分实际上并没变成实心的。这只是由于用有限的常识去理解无限的结果。图像由Morn the Gorn提供,维基共享资源。
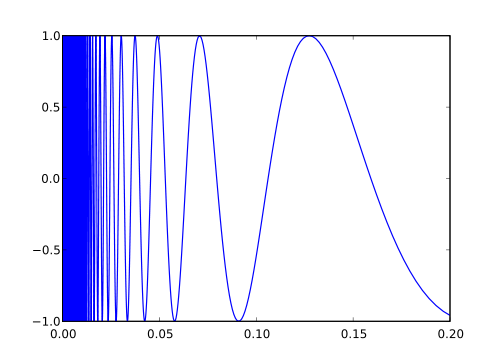
这个空间是函数 f(x)=sin(1/x)在(0,1]区间加点(0,0)的图像。我们可以看见随着x接近0,1/x越来越大,所以sin(1/x)在-1到1之间剧烈震荡。拓扑学家的正弦曲线是数学系学生看到的第一个例子,它连通但非道路连通。你可以看见他的终点线,但你不能从这儿到那儿去。
为什么连通?让我们尝试着将它分到两个不相交的开集。其中的一个集合包含点(0,0)因为是开集,它也包含以(0,0)为中心的领域内。无论多么小的领域内它都将包含一些x正半轴的点和在y轴上的0点。也就是说着它将包含一些f(x)的图像。这就意味着如果我们想要分裂空间我们不得不将函数f(x)的图像的一部分分到一个集合,而剩下的部分分到另一个集合。但是这儿没有办法分裂这个图像,是连续的曲线,就像实轴一样是连通的。
那为何拓扑学家的正弦曲线不是道路连通的呢?假设你正尝试着从 f(x)图像上的一点到(0,0)点,你将会一直走,走到永远。你会真的真的很接近它,但总会有一条无限长的路还在你面前。
一个密切相关的空间是封闭的拓扑学家的正弦曲线。一个封闭的空间包含所有边界点,边界点意味着可以任意接近集合里面的点。随着曲线f(x)震荡,所有在y轴上-1到1之间的点越来越接近曲线上的点,所以为了使拓扑学家的正弦曲线成为闭集,我们也在y轴上划分一个-1到1的线段,作为边界。这样不会破坏其他的拓扑性质——它依然连通但非道路连通——但是现在也封闭了。有些人喜欢玩这样玩儿。
如果你之前学过拓扑学,你可能看到过一条称做紧致性的拓扑学性质的定义:一个集合是紧致的,如果每一个开覆盖都有有限子覆盖。拓扑学家的正弦曲线不是紧致的,但是封闭的拓扑学家的正弦曲线却是。本着挫败数学教科书的精神,我将为读者留下一个思考题:找出拓扑学家的正弦曲线的一个开覆盖但是没有有限子覆盖,然后指出为什么这例子在封闭的拓扑学家正弦曲线中不成立。在一个闭,不可数,无处稠密的[0,1]区间的子集之后写下你的答案,然后送到康托广场,Log2(3)邮箱
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
作者,小米,哆嗒数学网翻译组成员。
A drunk man will find his way home, but a drunk bird may get lost forever. —— Kakutani
醉鬼总能找到回家的路;但是喝醉了的鸟儿可能永远回不了家。 —— 角谷静夫

今天我们要谈的是一个概率论中的重要结论:Z^d上的随机游走当d≥3时是非常返的,而当d=1,2时是常返的。
Z^d在这里表示由d 维欧氏空间中全体整点(即坐标全为整数的点)构成的集合。想象有一只青蛙以秒为时间单位在Z^d上做随机游走,那么它将按如下规则运动:在初始时刻(记为第0秒),青蛙位于原点;在每一秒钟,青蛙都会等概率地跳到某一个与它上一秒所在位置相邻的整点。由于Z^d上的每个整点都有2d个邻居,因此这个概率也就是1/(2d)(见下图)。

我们这里介绍的随机游走看似一个简单的数学模型,其实它的应用十分广泛。最常见的例子有物理学中布朗运动,金融市场中股票价格波动等等。
那么我们的问题就是,既然青蛙一开始位于原点,那是否总存在一个(随机)时刻T,使得第T秒时青蛙又回到原点呢?如果是,那么我们就称这样随机游走是“常返”的,否则就称是“非常返”的。

事实上,我们总可以假设存在一个介于0和1之间的实数p,它就是青蛙回到原点的概率。仔细想想,其实p的存在性本身也是不平凡的,因为我们知道古典概率论中,事件的概率只涉及到有限个变量,而这里回到原点的行为却与青蛙在无穷时间内的行为有关。当然,在公理化概率论中,通过建立起合适的概率空间,我们可以说明这样的p是存在的。这样,我们通过引入p,判断常返性就转化为判断p是否等于1的问题了,因为“总能回到原点”用概率论的语言来说就是“以概率1回到原点”。
下面我们来看随机游走另一个有趣的性质:马氏性。我们注意到,对于任意给定的时刻,比如第100秒,第100秒后的青蛙的位置只取决于第100秒时青蛙的位置,而前100秒的时间里,青蛙如何跳到这一位置方式无关。这就是所谓的“马氏性”,即给定现在,未来和过去独立。随机游走还具有“强马氏性”。所谓“强马氏性”,是指可以把前述的“第100秒”换成任意“只取决于历史的随机时间”(这样的时间又叫停时)。比如我们定义T成为青蛙第一次回到原点的时刻,那么T就是一个停时,并且关于T的强马氏性可以这么理解为:在随机时间T之后发生的事情,与在随机时间T之间发生的事情无关,因为我们知道在第T秒,青蛙又回到原点了,所以在时间T后开始的随机游走与一开始从原点出发的随机游走将遵循同样的规律。
如果要解释什么叫“只取决于历史”,不妨看一个买卖股票的例子。比如说你今天想卖出一只股票,你当然希望可以在一天当中最高价的时候卖。但很遗憾,除了碰运气,这是不可能做到的,因为除非一天已经结束了,没人能知道股价什么时候位于最高点。相反,如果你的策略是,“如果股票价格位于过去12个小时内的最高点就卖出股票”,那这就是一个可行的策略。后面这个策略中的交易时间就是一个“只取决于历史”的随机时间,也就是停时,而前者“一天当中的最高价”则不是停时。
如果你没看懂上面一大串关于马氏链和停时的描述,没关系,你一定也可以直观地理解以下结论。如果从原点出发的青蛙以概率p会回到原点,那么青蛙一定会以概率p^2(p^n表示p的n次方,下文相同)回到原点两次,这是因为,青蛙回到原点两次=青蛙回到原点1次+青蛙从原点出发再回到原点1次。由强马氏性,拆分后的第二个事件的(条件)概率也是p;因此,青蛙回到原点两次的概率就是p^2。同理,青蛙会以概率p^3回到原点3次,以概率p^4回到原点4次,等等。如果我们把青蛙回到原点的总次数记为N,那么上面的计算表明P(N≥k) = p^k,也就是说N是一个服从几何分布的随机变量。当p=1时,上述论证依然成立,只不过我们得到的N是一个取值恒为+∞的随机变量。
于是,根据几何分布的期望公式,我们得到了N的期望为EN = 1/(1-p);同样地,当p=1时,该式理解为EN=+∞。因此,EN是有限还是无穷,就刻画了随机游走是否常返。
我们还可以从另一个角度来计算EN。令X(n)为第n秒青蛙所在的位置,而an是取值0和1的随机变量,其中a(n)=1当且仅当X(n)=0,即a(n)=1当且仅当第n秒青蛙位于原点。根据定义我们得到N是全体a(n)的和,也就是N=a(1) + a(2) +…+ a(n) +… 这是显然的,因为整个数列(a(n))中有多少个1,就代表青蛙返回了多少次原点。
当我们对以上无穷和式取期望,并根据期望的线性性,交换无穷求和与求期望的顺序(这里能够换序是因为涉及的项an都是非负的,因此满足换序的条件),我们得到
EN = E(a(1) + a(2) +…+ a(n) +…) = E a(1) + E a(2) +...+E a(n) +...
等等,E a(n) 是什么呢?根据定义,E a(n) = P(X(n)= 0),正是第n秒青蛙恰好位于原点的概率!计算这个概率就是一个组合问题了,而判断常返性则变成了一个判断无穷级数敛散性的问题。
记A(n)= E a(n) = P(X(n)= 0)。下面我们的目标就是对A(n)进行估计,并由此判断无穷级数∑A(n)是否收敛。
在一维(d=1)时,如何计算An呢?注意到每一秒钟青蛙必须向左跳或者向后跳。因此在第n秒回到原点的必要条件就是n为偶数。而当n为偶数时,青蛙必须恰好有n/2的时间向左跳,有n/2的时间向右跳,才能在第n秒回到原点。我们知道每秒钟青蛙向左和向右的概率都是1/2,那么利用组合数公式,我们就得到
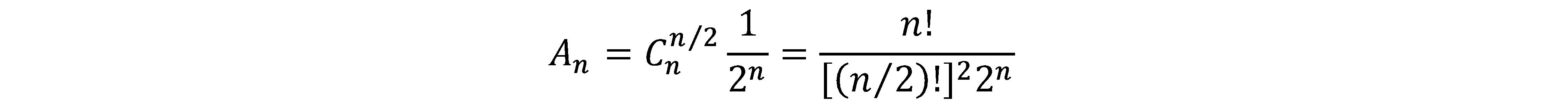
对于阶乘,斯特林公式给出了渐近公式:m! ∼(m/e)^n·sqrt(2πn) (sqrt表示开二次根号,下同)。代入A(n)的表达式,我们得到A(n)∼1/n·sqrt(2/π)这个渐近关系当然只限于n为偶数)。微积分中熟知的结论是p级数∑1/n^p收敛当且仅当p>1,否则发散。于是我们得到∑A(n)在d=1时发散,也就是说一维随机游走是常返的。
如果我们在高维时采用类似的方法,就能得到A(n) ∼ c· n^(-d/2),其中c是与d有关的一个常数。同样再借助p级数的知识,就能得到当且仅当d/2 > 1时,也就是d ≥3时,随机游走不常返;相反,d=1,2时,随机游走常返。
为了避免复杂的组合数估计,我们也可以从另一个简单的事实中看出A(n)的阶就是n^(-d/2)。如果我们令y(n)=X(n)-X(n-1)为第n秒时青蛙的位移,容易看出所有y(n)都是独立同分布的随机单位向量。由中心极限定理,Z(n) :=X(n)/sqrt(n) = (y(1) + y(2) + … y(n))/sqrt(n)将趋向于一个d维正态分布Z。那X(n)=0意味着什么呢?由于X(n)只能取整点,那么X(n)= 0表明Z(n)的取值大约位于原点附近一个边长为的1/sqrt(n)小正方体中。根据中心极限定理,Z(n)的取值落于这个小正方体中的概率与Z是差不多的,而对于后者,这样的概率恰恰就约等于小正方体的体积,(1/sqrt(n))^d(注意到是d维空间),乘以原点处Z的密度函数大小,一个非零的常数。这样我们就很容易得到了A(n) ∼ c· n^(-d/2)这个结论。
如果要把这个随机游走的小结论用于生活中,我们也许会为再也不用担心认不得路而感到欣慰,因为二维随机游走是常返的,就算是不认识路随便乱走,也总能到达任何想去的地方!当然这句话既对也错;对的地方在于,由常返性,确实总存在一个时间T,在平面上随机游走的你也能走到任意想去的地方;错的地方在于,更进一步的理论表明,这个随机时间T是一个期望为无穷的随机变量,也就是从平均的意义上说,你永远也到不了目的地!
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Evelyn Lamb,数学及科学普及自由作家
原文作者,Evelyn Lamb,数学及科学普及自由作家。
翻译作者,e^iπ+1=0,哆嗒数学网翻译组成员。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
上回我们写了一篇关于康托集的文章,它是一个将小与大统一起来的有趣的数学空间。
说小是因为它的长度只有零,但是说大是因为它本身是个不可数的集合。
一旦一个数学家着手处理一个数学对象,直觉上第一步便是试着摆弄它,然后看看会发生什么。这使我们得到了胖康托集(编者注:Fat Cantor Set 正规教材上译为类康托集,但是本文要显示他比康托集“肥硕”于是就这样翻译了)。
当有人提起康托集时,他们指的是标准三分康托集,也就是我之前提到的那个康托集。
这个集合的构造是通过将区间[0,1]中间三分之一的部分移除,只留下区间[0,1/3] 和 [2/3,1]。
然后将剩下的每个区间再去掉各自的中间三分之一,这样的操作一直重复下去。
令人惊奇的是,这样的操作使得这个区间还有一些东西留下,却没有长度。
而被移除的区间长度总和是1,而这就是原来区间的长度。

第一个能想到的符合逻辑的操作就是将康托集移除三分之一这个比例换成其他的比例。
如果我们只移除每个区间中间的四分之一会产生什么样的结果呢?
我们同样从区间[0,1]开始操作。
第一步,我们只留下区间[0,3/8] 和 [5/8,1]。
然后我们继续移除每个区间中间四分之一的区间(移除的区间长度变为3/32)。
你可能会认为会有更多的东西被留下,因为我们每步移除了更短的区间,但这个想法是不对的。
如果你将所有移除的区间长度都加在一起,我们仍旧得到1。
这个康托集实际上并没有比我们之前那个集合更有趣。
当然我们也没有变得更不幸运。
如果我们保证每次移除区间所用的比例都是一样的,那我们总能得到移除的区间长度总和为1。
当然有很多方法区别那些移除中间三分之一,四分之一,或者任何一个比例的康托集,但是现在我们准备试着对康托集做很不一样的操作。
第二件我们可以做的事情是改变每次移除区间时所用的比例。
我们将再次从区间[0,1]中移除中间四分之一的区间,这样我们留下区间[0,3/8]和[5/8,1]。
但是到了第二步,我们将从每个剩余的区间中移除它中间一个长为十六分之一的区间。
这时候,情况已经发生了些许变化。
之前的时候,我们从每个剩余区间移除了长为三十二分之三的区间,这比起十六分之一稍微长上一些。
在新的构造中,我们将不断改变每一步里剩余区间需要去除的区间长度。

在第一步中,我们移除了初始区间的四分之一。
在第二步中,我们从每个剩余区间移除长为十六分之一的区间,相较于初始区间,共移除了八分之一。
在第三步中,我们每个剩余区间移除了长为六十四分之一的区间,相较于初始区间,共移除了十六分之一。
我们可以继续这样的操作,到了第n步的时候,我们将移除整段区间1/2n+1的长度。
如果这个步骤无限地做下去,我们总共移除的长度将会是1/4+1/8+1/16+…,而它的和则是1/2。
这时候我们的确得到了一些新的东西!
这个结构被称作史密斯-沃尔泰拉-康托集合,或者是胖康托集。
康托集的一维测度是0,这是因为我们移除的区间长度和等于一开始的区间长度,但是胖康托集还留下了一些东西——从整个[0,1]区间里留下整整一半。
那这些是从哪里来的呢?
根据构造过程,胖康托集不包含任何区间。
每当我们看到一个区间,我们都要移除这个区间中的一部分。
某种程度上,有一些长度是被留下了,但不是以我们熟悉的方式留下的。
如果我们试图用手去抓,只能抓到一把灰尘。
康托集挑战了我对小与大的直觉认识。
胖康托集更将我的直觉完全吹散了。
一个没有任何微小片段的一维物体究竟是怎样获得一定长度的?
当然,这样说其实不完全公平。
在区间[0,1]上的所有无理数组成的集合,它的一维测度为1,长到居然与整个区间一样,但是这个听上去并没有那么的违反直觉。
无理数无处不在。
所以,你在数轴上随便一扫,都能扫到无理数。
在数学上,我们把这种情况叫做区间上稠密,或者在所有实数构成的集合中,无论怎么样选择一个子区间,无论有多小,都会包含着无理数。
是否稠密这一问题使得胖康托集变得更奇怪。
胖康托集在[0,1]区间上不是稠密的,而且他们甚至在任何更小的区间上都不是稠密的。
无论你的区间取得多么小,你都能找到一个完整的区间,其中任何一点都不在胖康托集中。
我们将这种情况叫做无处稠密(nowhere dense)。
这样胖康托集的长度是1/2就没什么稀奇的地方了。
事实上,调整每一步需要移除的区间长度,我们可以得到一个按照我们想要的任意长度的康托集。
我们不能得到一个长度为1的胖康托集,但是我们可以得到一个长度趋近于1的胖康托集。
无论我们将胖康托集塑造的多大,他们都不会占满任何一个区间,并且会无处稠密。
那我们可以在哪里看到他们呢?
我第一次遇到康托集的地方就是康托函数,这我提到过了。
康托函数,或者说是魔鬼的楼梯,向我们展示了联系了微分与积分的微积分基本定理的局限性。
事实上胖康托集也能做到这一点。
特别地,意大利数学家沃尔泰拉 (Volterra ,1860-1940)利用胖康托集构造了一个可微函数但是导函数不可积。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Evelyn Lamb,数学及科学普及自由作家。
翻译作者,金星光,哆嗒数学网翻译组成员。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
康托尔集很庞大,但它当中几乎不含有任何“内容物”。
上个月,我写了关于π-Base网站的一些文章,这个网站与《拓扑学中的反例》这本书起着相似的作用。碰巧这学期我教授拓扑学这门课程,因此去回顾这些有价值的反例是件有趣的事情。作为博客上的一个新系列,我将会写一些看似怪异但不乏趣味性的数学空间的文章。我们就以康托尔集开始吧,这个有用的空间一直活跃在全世界的数学领域中。
通常有两种主要的方式来思考和理解康托尔集,我们先以第一种比较有趣的思考方式开始吧。我们先画出一条从0到1的线段,并且包含端点,因此我们得到闭区间[0,1]。现在我们将这个区间三等分,去掉中间的开区间(1/3,2/3),然后我们就会得到[0,1/3]和[2/3,1]这两个闭区间。接着我们分别从中间去掉[0,1/3]和[2/3,1]这两个区间中间的1/3,我们就会得到[0,1/9]、[2/9,1/3]、[2/3,7/9]和[8/9,1]这四个区间。如果我们按照以上的方式继续做下去的话,我们就会得到康托尔集。
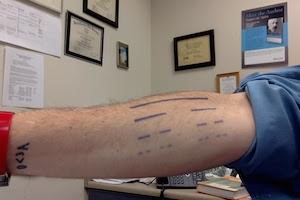
可能稍微令人惊奇的是,当你继续上述的所有步骤之后,几乎没有什么东西剩下。但是如果你进一步的思考,你将会发现0 , 1/3 , 2/3 , 1以及子区间的端点并没有被去掉。更令人惊讶的是,不仅仅是这些端点,还有非常多其他点, 因为端点数量只有可数个,但是整个康托尔集却是个不可数的集合。想要弄清楚原因,就让我们以另一方式来重新思考康托尔集吧。
第二种描述康托尔集的方式虽然有些枯燥但会更加精确。我们通常以十进制来书写数字,但除了这种书写方法以外我们还可以以三进制来书写数字,这就意味着我们只需要数字0、1和2就可以了(十进制书写的1到10如果以三进制来书写就会写成1、2、10、11、12、20、21、22、100、101)。康托尔集是闭区间从0到1的数字中,那些在三进制中仅用0和2书写的数字的集合。例如,0是包含于康托尔集中的,至于1可以被写成0.22222....(就像0.9999...=1那样)。
用三进制的方式来思考康托尔集特别自然地符合康托尔集的构造。将闭区间[0,1]中的所有数字用三进制转换。当你去掉区间(1/3,2/3),你就同时在去掉这个集合中三进制小数中第一个小数位为1的点。当你去掉剩下区间的1/3,你就同时在去掉三进制小数中第二位小数为1的点,以此类推。但我们确实要对端点值小心。早期的时候,我们注意到数字1可以被写成1或0.2222...类似地1/3可以被写成0.1或者0.0222222...。任何用三进制书写的数字如果以1收尾都可以用2的无限循环来代替,康托尔集是三进制中仅用0和2表示的数的集合,但这并不意味着这个集合中的所有数字一定要按照这种方式来书写,因此我们允许1、1/3以及诸如此类的数字成为这个集合中的一部分。
康托尔集并不仅仅是一个可以纹在身上的炫酷的事物,它也拥有许多很好的性质出现在早期的拓扑学和分析学的课堂上,你也可以用它来测试一些拓扑学和分析学中的一些新的定义。它将“大”和“小”的特性有趣的结合到一起。我在前文提到康托尔集是个不可数集。在去年夏天我写过一些有关不可数集合的文章。可数集的定义依赖于集合中的元素可列,即使我们不能写下整数集所有的元素,但是我们能够想出一种方法去列出它们,知道每个整数将会出现在数列中的哪个具体的位置上,因此整数集是可数的。令人吃惊的是,一些看似很大的集合依然是可数的。最令我吃惊的要数有理数集啦,有理数集理应要比整数集“大”,但准确来说,有理数集与整数集具有相同的元素个数。
实数集是不可数集。这意味着任何我们想要列出这个集合所有元素的方法都将以失败告终。康托尔的对角化论证,完美的证明了这一点,这是我最喜欢的数学证明。同样的方法可以证明康托尔集是不可数的,事实上它与实数集的元素个数相同。
这就是康托尔集开始成为反例开始的地方。它是不可数的,但它也没有包含任何“内容物”。它的长度是零。一种方法去注意到这一点是在于你每一步都去掉剩下某个区间长度的1/3.第一步,你去掉闭区间[0,1]这个区间长度的1/3,第二步你又去掉剩下区间长度的1/3,总共去掉了2/9.你去掉的长度总和是1/3 + 1/3 × 2/3 + 1/3 × 4/9 + 1/3×8/27 + …很容易的计算出这个几何级数的和为1。而这个区间的长度为1,我们去掉1个单位长度,最后却得到了多达整个实数数量的康托尔集。
如果你想要了解更多有关康托尔集的知识,π-Base列出了很多它的拓扑性质:它是紧致,完全分离,拓扑完备,非无核集(无核集定义:非空闭子集必有孤立点——编者注)。Cut-the-knot math有更丰富的有关康托尔集的知识,Robert Vallin(上述图片中有康托尔集纹身的人) 写了一本有关康托集的书。祝大家阅读愉快!
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
美国有多个机构对大学进行排名,其中最有影响力的就是由《美国新闻和世界报导》在每年下半年公布排名,也就是常说的每年的USNEWS排名。2017年10月26日,2018年USNEWS全球最佳大学排名已经公布。在最佳大学名单上,前四名和上一次没有变化,哈佛大学、麻省理工学院、斯坦福大学、加州大学伯克利分校四所美国大学分列前四。
我们哆嗒数学网的小编最关心的还是数学学科的排名。共有200所大学列入数学排名的榜单。这一次排名第一不再是来自美国的高校,而是来自法国的巴黎第六大学。斯坦福大学和普林斯顿大学分列二、三名。由于第10名并列,所以有11所大学进入前10名,第四到第十分别为:麻省理工学院、加州大学伯克利分校、牛津大学、纽约大学、哈佛大学、剑桥大学、苏黎世联邦理工学院(并列第十)、芝加哥大学(并列第十)。
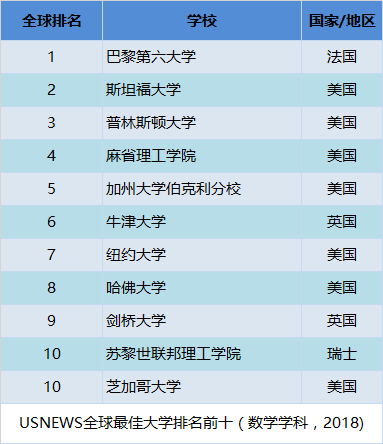
亚洲共有48所大学进入排名,其中来自中国的高校占据28个席位。前10名中,中国占据6席(内地5席,香港1席),伊朗、韩国、日本、新加坡各占一席。亚洲第一的是北京大学,第二名是来自伊朗的伊斯兰自由大学,第三名复旦大学。
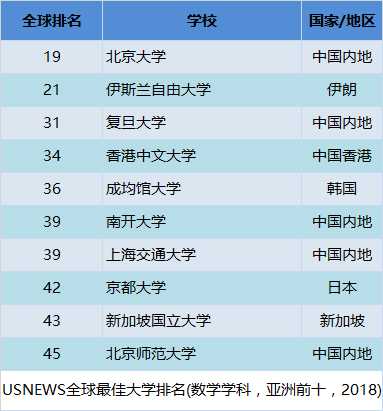
而中国榜单方面,前三名是北京大学、复旦大学、香港中文大学。第四到十名分别为:南开大学(并列第四)、上海交通大学(并列第四)、北京师范大学、香港理工大学、清华大学、香港城市大学。
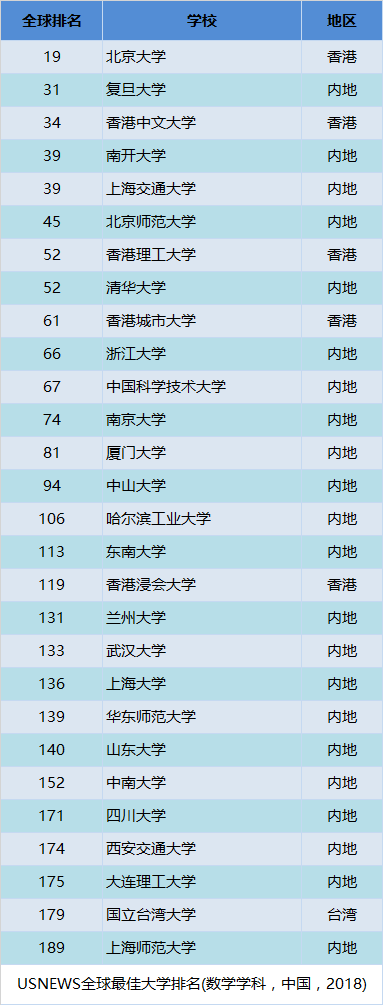
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

作者,【陌生,爱),哆嗒数学网群友,就读于湖北理工学院。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
今天小编想给大家讲一下行列式,诸位看到行列式是不是觉得特别亲切,大一的时候学习行列式有没有很痛苦啊?——反正当年小编学习这个是及其痛苦的——也许我比较笨吧,:)。
是否还记得《线性代数》或者《高等代数》里面的行列式定义?一般的教材对行列式的定义大概两种吧,逆序定义和展开式定义,无论哪种定义方法,都让我当你感觉莫名其妙,一直要到很后面学习了线性方程组,建立了方程与行列式的联系,才知道这些定义的意义。在没有任何直观意义的帮助下,学习行列式的各类性质简直和死记硬背没有区别。
今天小编抛开这些通常线性代数或者高等代数教材上的定义,从几何上让读者们更直观的理解什么是行列式,并用几何方法来介绍行列式的基本性质。
那我们现在开始来说说行列式吧!首先来看简单的二阶行列式:
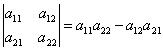
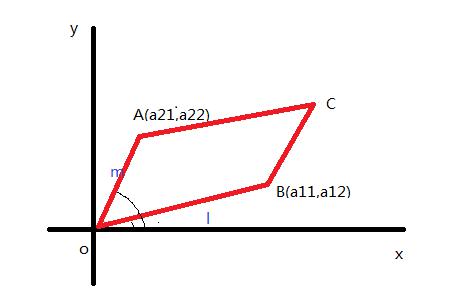
如上图,平行四边形OACB的面积为:
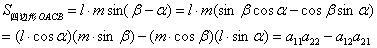
毫不意外的(取m = l = 1),我们用这种方式来记忆和角公式:
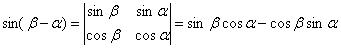
因此二阶行列式的值,可以表示两个向量所构成的平行四边形的面积。那么三阶行列式表示什么含义呢?n阶行列式又代表什么含义呢?类推一下相信大家就能想出来。没错三阶行列式的几何意义为三维欧式空间里平行六面体的体积。当然n阶行列式就由n个n维向量组成,其结果为n维平行多面体的体积。
下面的文字我们将来解释行列式基本性质的几何意义了。下面我们一起来看行列式性质的几何解释,这里我们取二阶或者三阶行列式进行说明。
性质1:行列互换行列式不变(转置)。
数学语言表述为:
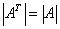
几何解释:很显然平行四边形两条邻边互换,它的面积依然不变。
这说明行列式的行和列等价,也就是说凡是对行成立的性质,对列也成立。
性质2:以一常数乘行列式的一行就相当于用这个数乘以此行列式。
数学表述为:
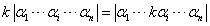
对于二阶行列式,我们看上图就很直观,我们将其中一个向量变成原来的k倍,面积也跟着变成了原来的k倍。
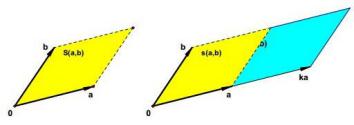
类似的三阶行列式有,平行六面体体积的k倍相当于其中一个向量变成原来的k倍。平行六面体体积的增大可以看成其中某个棱长增大相应的倍数。
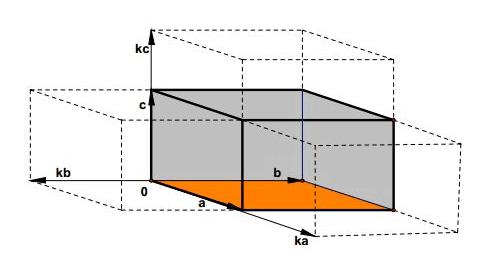
性质3:如果某一行是两组数的和,那么这个行列式就等于两个行列式的和,而这两个行列式除这一行以外全与原来的行列式对应的行一样。
数学表述为:
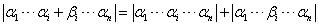
如图所示,图中的紫色平行六面体的体积可以看成两个小平行六面体的体积之和,也就是说一个行列式可以通过拆分其中的一个列向量得到两个行列式的和。
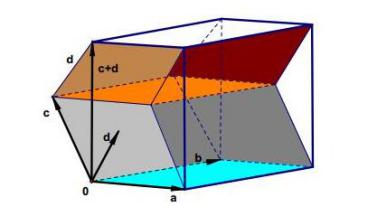
性质4:如果行列式两行成比例那么行列式为零。
数学表述为:
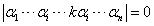
先考了特殊情形,当k取1时,也就是说行列式有两列或者两行元素相等时,它所对应的空间平行六面体的两条邻边重合,相应的就是将平行六面体压成高度为零的二维平行四边形,其体积为零,即行列式为零。当k不等于1时,相对应这组向量里面有共线的向量,即由n维降低到n-1维,对应的度量体积为零。
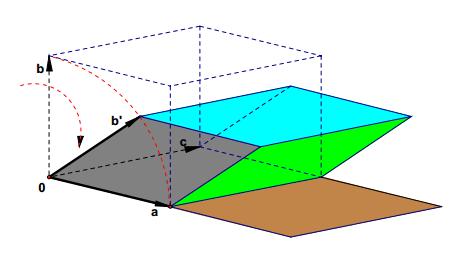
性质5:把一行的倍数加到另一行,行列式不变。
数学表述为:
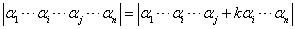
这条性质表述为,以向量a和b为底的平行六面体在向量a方向上做切向变换。我们知道将平行六面体平推它的体积依然不变。故对应行列式的值不变。
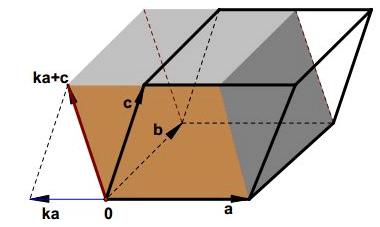
性质6:对换行列式两行的位置行列式取反号。数学表述为:
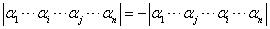
因为向量具有方向性,如果我们把符合右手定则的向量积定义为正值的话,则它的反向定义为负值。当det(A)为负值时它就确定了原像的一个反射。
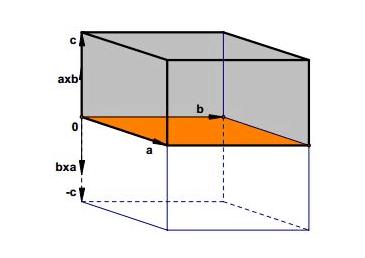
其实一个行列式的几何意义是有向线段(一阶行列式)或有向面积(二阶行列式)或有向体积(高阶行列式)。行列式是由各自坐标轴上的有向线段所围起来的有向体积的和。这就累加要注意方向,同向相加,反向相减。
相信读者应该理解了行列式的几何意义了吧,是不是对行列式有了更新的认识啊?其实小编一直的觉得很多数学量或者数学概念,都可以找出它所对应的直观意义,这样我们的数学学习就不会那么抽象那么难理解了,反而会很有意思。
最后希望大家能喜欢数学,反正小编就很喜欢数学——数学虐我千百遍,我却待它如初恋——不管你信不信,反正我自己都不信,啊哈哈哈哈~~~。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
还记得之前提到的上海交大的世界大学学术排名吗?现在这个排名更名为软科世界大学学术排名了。2017年10月12日,该机构公布了“中国最好学科排名”,包括91个一级学科,其中也包括了数学排名。
这次排名的排名依据包括“高端人才”、“科研项目”、“成果获奖”、“学术论文”、“人才培养”五个大指标。每个大指标又有几个小指标,如何你有兴趣,可以去该排名的官网查看(http://zuihaodaxue.com/BCSR/best_chinese_subjects_rankings_methodology_2017.html)。
数学排名公布了前120名的学校,共123所学校进入榜单。第一名是北京大学,复旦大学和山东大学分列第二、三名。第四到十名分别是中国科学技术大学、清华大学、中山大学、四川大学、浙江大学、西安交通大学、上海交通大学。
以下是详细榜单,我们多任何排名的意见都是——你有意见可以提!

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
诺贝尔奖没有设立数学奖,每年诺贝尔奖颁奖的时候似乎都没有数学家什么事情。数学作为一个人类学术的大学科,诺贝尔奖作为最受关注的学术奖项,没有数学奖怎么看似乎都不太合适。
诺贝尔奖由六个大奖项,分别是物理奖、化学奖、医学奖、文学奖、和平奖、经济学奖。数学家在诺贝尔奖里一直没闲着,几乎每一个奖都闪现过数学家的身影。
1、 物理学奖
代表数学家:马克斯·波恩,1954年,因“在量子力学领域的基础研究,特别是他对波函数的统计解释”获奖。
虽然一般被认为波恩是位物理学家,但是wiki上也吧数学家的头衔给了他。波恩在哥廷根大学攻读博士的时候,跟着当时最牛三位数学家——希尔伯特、闵可夫斯基、克莱因——学习过数学。后来拿的学位也是数学博士学位。而波恩的物理学研究,其实用到的非常艰深的数学方法,留下来的一些东西,其实现在数学家也在研究。
2、 化学奖
代表数学家:约翰·波普,1985年,因“发展了量子化学中的计算方法”获奖。

虽然波普一般被认为是理论化学家,但波普自认为自己首先是个数学家,然后才是化学家。实际上,波普博士拿的是数学学位,毕业后,还在剑桥大学数学系当过一段时间讲师,自己的化学研究也用到非常高级的数学方法。所以,波普拥有数学家头衔也不算过分。但是,波普的化学同行们却不这么认为,他们坚定的人波普是一个绝对的化学家,然后数学家的身份嘛——他们得考虑一下。
3、 经济学奖
代表数学家: 约翰·纳什,1994年,因“在非合作博弈的均衡分析理论方面做出了开创性的贡献,对博弈论和经济学产生了重大影响”获奖。

纳什绝对是一个伟大的数学家,然后顺便拿了个诺贝尔经济学奖。得诺贝尔奖的博弈论,虽然在经济领域应用较多,但也被认为是数学的一个分支。另外,纳什在他27岁时的一个微分几何的成果,也被认为是数学最高奖菲尔兹奖级别的成果。凭借微分几何的贡献,纳什在2015年获得过数学三大奖之一的阿贝尔奖。故事的结局是悲剧的,在纳什领完阿贝尔奖回国后,死于回家路上的车祸。
如果说物理、化学算是数理化不分家,而经济领域本身和数据打交道比较多,数学家拿奖还算可以理解的话,下面的奖就慢慢的让你感到数学的神奇了。
4、 生理学或医学奖
代表数学家:阿兰·柯马克,1979年,因“创立计算机X射线断层成像(CT)的数学理论”获奖。

1979年的诺贝尔医学奖的授奖发言中说到:“今年诺贝尔医学及生理奖的两位获奖者都不是医学专家,然而他们在医学领域掀起了一场革命…… 他们所发明的计算机辅助X射线成像技术,使医学如同进入了太空时代。”柯马克的主业是物理,然后在与一家医院的合作项目中,将其遇到的问题转化为了一个数学问题,并写成了论文。论文中完全没提到CT什么的。后来,人们开始研究CT的工作原理,发现几十年前柯马克的这篇论文已经建立起了数学的理论框架。
但数学家们的表演还没有结束.......
5、 文学奖
代表数学家: 帕特兰·罗素,1950年,因“表彰他所写的捍卫人道主义理想和思想自由的多种多样意义重大的作品”获奖。

用“不想拿文学奖的数学家不是好的哲学家”这句话来描述罗素是再好不过了。罗素与怀特海合著的《数学原理》是第一部试图形式化所有数学的专著。而他提出的“罗素悖论”引发了数学界对数学理论底层更加深刻的讨论。罗素还是上个世纪最重要的哲学家之一,和另外几位哲学大咖一起创立了分析哲学。另外,他的一部《婚姻与道德》帮他获得了诺贝尔文学奖。
6、 和平奖
代表数学家:莱纳斯·鲍林,1962年,因“反对核弹在地面测试的行动”获奖。
经管鲍林的化学研究用到了很多数学分析工具,但他是绝对的化学家。把鲍林列为数学家似乎有些牵强,但是小编在查阅鲍林获得过的奖项的时候,发现他在1957年获得过费马数学奖章(Pierre Fermat Medal in Mathematics)。注意,这是一个比1989年才开始颁发的费马奖(Fermat Prize)更久远的奖项,按wiki上的说法,鲍林的获奖是“300年内仅有6次颁奖中的一次”。于是,列为数学家应该也不为过吧。鲍林先在1954年得了诺贝尔化学奖,然后在1962年获得诺贝尔和平奖。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
根据中华人民共和国教育部官网消息,教育部、财政部、国家发展改革委联合发布了《教育部 财政部 国家发展改革委关于公布世界一流大学和一流学科建设高校及建设学科名单的通知》,该通知附件中公布了世界一流大学和一流学科(简称“双一流”)建设高校及建设学科名单。
“双一流”建设学科名单中,数学作为建设学科的学校一共有14所,均没有添加“自定”标示。按文件中的说法,说明所有以数学学科为“双一流”建设学科的学校均为“根据‘双一流’建设专家委员会确定的标准而认定的学科”。(注,有“自定”标示的学科为“‘双一流’建设专家委员会建议由高校自主确定的学科”)
这14所以数学学科为“双一流”建设学科的学校是(以学校编码为序):北京大学、清华大学、北京师范大学、首都师范大学、南开大学、吉林大学、东北师范大学、复旦大学、上海交通大学、中国科学技术大学、山东大学、中南大学、中山大学、四川大学。
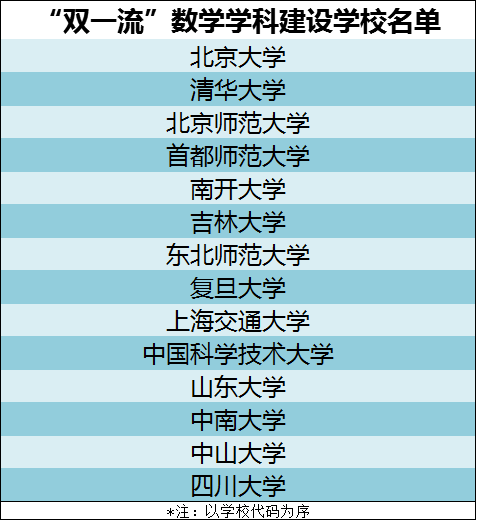
我们哆嗒数学网的小编注意到,一般人们认为的数学强校没有出现在这14所大学的名单中,比如浙江大学、南京大学、武汉大学、华东师范大学等。
同时,也应该注意到进入“双一流”的名单不意味着这些学校的学科已经成为“一流”。是否成为“世界一流”取决于未来该学校的建设和努力。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
下面的笑话可能会引起部分读者的不适,不喜勿入。
先来几个复变函数的笑话。
你好,您拨打的电话号码是imaginary的,请将您手机旋转90度再拨。
如果J表示一个笑话,那么P+iJ就是一个非常非常冷的complex笑话。
——你没觉得好笑,是因为笑话J在imaginary part .
π和i是一对恋人,π总对i说:“你现实点吧!”,i总是回应:“你怎么就不讲道理!”

为什么数学家都把他家的狗取名叫柯西?
——因为它们总会在每个pole周围留下residue.
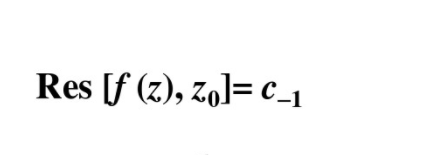
再来几个是关于log(对数?木头?)的故事,注意国外一些书中的log和中文教科书的ln是一个意思。
1/carbin 求不定积分是什么?
log carbin !
——不,你忘了加一个常数C!

一位数学家落水了,会怎么呼救?
他会说: log log log log log...
这才是真正的Jordan标准型,其他的都是冒牌货!
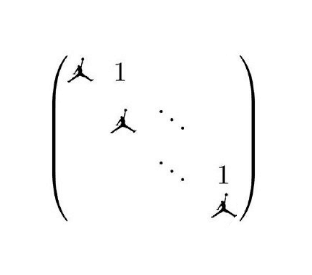
是的,没有什么比2n+1更odd了。
为什么数学家会把万圣节和圣诞节搞混?
因为 OCT 31 = DEC 25.
你是说polar bear?就是经过坐标变换会变成直角的熊?

“Thare are five mistukes im this centence——真的,还是假的?”
一根绳子看见了一位漂亮的小姐姐,上前搭讪。
“嗨,美女我们能加个微信吗?”
“滚!”
绳子觉得是自己的颜值问题,于是认真打扮了一番。他将自己打了一个结,并且磨破绳子的一端。
绳子又找到那位小姐姐。
“你好!......”
“怎么又是你,又来干嘛!”
“不不不,I’m a frayed knot! (I’m afraid not!)...”

耶稣为担我们的sin而死,那么有人会为了我们的cos和tan而死吗?

好吧!最后大家算算体积,就是你喜欢的Pizza!
当然,很好吃!
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
数学世界里有很多著名的难题,比如歌德巴赫猜想。歌德巴赫猜想作为一个世界难题之所以著名,是因为问题本身太容易表达了,表达出来后,一个小学生都能看懂。如果,把这个样的问题放在教材课后的习题部分,不知道能坑掉多少脑细胞。
然而,数学就是这么神奇,一些数学问题的表述非常简单,简单得就像课后的习题一样。但要解决他们非常困难。就像他们故意伪装成课后习题似的。下面的10个问题大概就是这样的问题。他们的表述非常简单,普通大二的理工科学生都能看懂,但至今无人能解决。
第十名 数一数,素数和合数到底有多少的问题
习题伪装指数:☆
如果学过初等数论,我们由素数定理可以简单的认为素数在自然数中的密度为零。那么我乱扔一个其他形式的一堆自然数,其中素数的密度也是零吗?
问题:形如2^n+5的自然数几乎都是合数。( 2^n表示2的n次方,几乎的意思是指密度为1 )
好吧,看懂这个似乎要至少学过初等数论。但是不是所有理工科的朋友都学过这门课。但这个问题真的很难,至今不知道怎么解决。
第九名 看上去是线性代数中找几组基的问题
习题伪装指数:★
线性代数相信大多数理工科的朋友都会学习。我相信,对线性空间这个名词并不陌生。对于n维线性空间,任意n个线性无关的向量都能组成该空间的一个基。现在,我们有B1,B2,...,Bi,...,Bn这n个向量组(wiki上要求两两不交,其实不要求也可以),每个向量组有n个向量,这些向量组都构成n维线性空间的一个基。于是这里,有n×n个向量。现在,把这个n×n个向量排成一个n×n矩阵,矩阵的第i行的n个元素,正好是Bi中的n个元素(这一行的顺序无所谓)。
问题:对任意给定的n个基,有没有一种排列办法,满足上述条件,而且矩阵中的每一列的n个向量都构成线性空间的一个基。
这个叫做罗塔基猜想,由罗塔在1989年提出。这其实是一个披着线性代数外衣的组合问题。这里只是提到它的线性代数版本,还有别的版本,比如流形版本。
第八名 一个忧伤故事引发的数学难题
习题伪装指数:★☆
一个忧伤的故事,有n个人(n>1)在半径为1千米的圆形跑道上匀速的跑圈,没有人静止不动(即速度大于0)。他们出发点相同,行走的方向相同,但没有任何两个人速度是相同的(就是说,n个人的速度两两不同)。跑道上的人感情很脆弱,当一个人和其他每个人的距离都大于等于1/n千米的时候,这个人会觉得自己很孤独。
问题:请证明对任意n,跑道上的人每一个人,都有孤独的时候!

这叫做孤独的跑者问题。这个问题非常难,目前的情况是,有人证明了n≤7的时候,命题成立。另外,陶哲轩证明了,对任意的n,只需要验证有限多种情况就可以判定命题是否成立。但就仅n=8的时候,那个分类的带来的计算量,已经不是地球上的计算机能处理的了。
第七名 集合求并集,找元素的“小问题”
习题伪装指数:★★
关于集合的知识,我们在高中就学了不少了。一个集合也可以是另外一个集合的元素,比如集合{{2,3,4},{1,4,6,9},{1,2,3,4,6,9}},{2,3,4}就是它的一个元素。一个由集合为元素组成的集合我们称为集族。如果一个集族里面任意两个元素并起来,还是这个集族里的元素,我们就说这个集族对并集运算封闭(因为集族里的元素都是集合,于是可以做并集运算)。
问题:一个有限的集族,集族的每个元素也都是有限集合。如果它对并集运算封闭,且不是{∅},那么是否一定有个元素,这个元素属于集族里至少一半的集合。比如,前面举的集合例子,它是一个3个集合组成的集族,而元素2是第一个和第三个集合的元素,超过3的一半。
此问题由彼得·弗兰克尔在1979年提出,叫做并集封闭集族猜想。快40年了,没人解决。目前的情况是,人们解决了集合数量不超过46个的集族的情况,以及集族中最少元素不超过两个的情况,这些时候答案都是肯定的。
第六名 一个求极限的问题,判定出来的极限值是什么
习题伪装指数:★★☆
我们的很多读者一定做过这样的习题,就是证明 1 + 1/2 + 1/3 + 1/4 + ...+ 1/n - ln(n) 在n→∞的时候,极限是存在的。用的办法是单调有界原理。我们把这个极限用符号γ表示,称作欧拉常数。
问题:判断欧拉常数γ是有理数还是无理数。
我们知道他的近似值,0.57721566490153... ,2003年有人用从对它的连分数研究中得到结果是:如果欧拉常数是有理数,那么它的分母将超过10的242080次方。但是依然离判断出结果很远。
第五名 貌似小学生都“知道”的有理数无理数问题
习题伪装指数:★★★
自然对数底e,圆周率π都是我们在中学里最常见的无理数。上了大学学习了高等数学或者数学分析后,我们有能力证明他们是无理数这件事情当然可能需要一些课外阅读)。但是我们对这两个数做四则运算后的结果,是有理数还是无理数却并不知道。
问题:判断e+π和eπ是有理数还是无理数。
这个问题似乎没看到希望。不过,你可以用韦达定理和e、π是超越数的事实,轻易的判断e+π和eπ不可能都是有理数。
第四名 好“简单”的级数敛散性判断“作业题”
习题伪装指数:★★★☆
我们在高等数学里学了很多种级数敛散性的方法。给一个看上去形式简单的级数,判断它收敛怎么看都是课后习题级别难度的问题。那么我们看看下面一个级数。
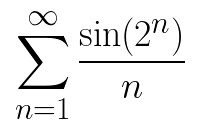
问题:上面的级数是否收敛?
这个问题其实是一个和π有关的数论问题。实际上很多看上去带sin的极限问题都是伪装成高等数学的超越数论问题,都和π有关系。
第三名 关于正整数乘乘除除的游戏
习题伪装指数:★★★★
我们来做一个游戏。给你一个正整数,如果它是偶数,我们把它除以2得到一个新的自然数,如果新的自然数还是偶数,继续除以2。这样一直除到他是奇数为止。对于这个奇数,我们把它乘以3再加上1,这样又得到一个偶数。我们再继续前面的操作——只要是偶数就除以2,奇数就乘以3加上1。这样一直操作下去,我们会得到一个无穷长度的正整数序列。
问题: 对任意给定的初始正整数,按上面操作的得到序列最终会归于4,2,1,4,2,1,4,2,1,... 的循环?
这叫做考拉兹猜想,也叫3n+1猜想。有人把这个问题作出了推广,有了这个猜想的推广版本。已经证明推广版本的猜想是一个算法不可判定问题——简单的说,不可能用计算机程序来证明推广版本的猜想。
第二名 把分数拆成分数单位的“小学奥数”题目
习题伪装指数:★★★★☆
我们小学就学习分数了。记得小学的奥数题目里,经常干一件事情,就是把一个分数拆成几个分数单位的和。下面的问题也和这个有关系。
问题:问题:对任意大于1的正整数n, 关于x,y,z的方程 4/n = 1/x + 1/y + 1/z , 是否都有正整数解?即4/n都能正好拆成三个分数单位的和。
这个问题叫做埃尔德什-施特劳斯猜想,1948年提出,已经快70年了。注意到 4/5 = 1/2 + 1/4 + 1/20 = 1/2 + 1/5 + 1/10,有两种写法。于是有人转而研究满足方程解的个数的规律(注意,如果有个n对应的解的个数是0,就否定了这个猜想)。2013年的结果是,解的个数相对于n的增长速度是不超过关于ln(n)的多项式级别的。
第一名 “非常简单”的不等式,但结果令人意外
习题伪装指数:★★★★★
诉说这个问题前,我们来看看这样两个函数。对于一个正整数n,我们把它所有的约数加起来,得到的正整数记为σ(n)。比如24的约数为1,2,3,4,6,8,12,24,那么σ(24) = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60。 同样是正整数n,我们把不大于它的所有正整数的倒数加起来,记为H(n), 就是说H(n)=1 + 1/2 + 1/3 + ... + 1/n . 比如H(3)= 1 + 1/2 + 1/3 = 11/6 。 通过σ(n)和H(n)我们构建如下的不等式:
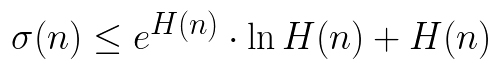
问题:对所有正整数n,是否都有上面的不等式成立。
如果我告诉你这个不等式问题是很多数学家心目中在整个数学界最重要的猜想,你信吗?2002年,一位数学家证明了此不等式与大名鼎鼎的黎曼猜想等价。也就是说,证明了这个不等式,也就证明了黎曼猜想。而黎曼猜想在数学界的地位,大家自行百度吧,至今还有人悬赏100万美元征解。黎曼猜想的原始版本,需要有复变函数的学习背景才能看懂,但这个版本,估计中学生都能看懂了。

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

原文作者:Rebecca Hills-Duty。
译文作者:Jessie仪,哆嗒数学网翻译组成员,就读于布里斯托大学。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

俄克拉荷马州立大学和佐治亚理工学院的数学家们正在尝试为生活带来一个不同的世界:通过创造一个虚拟现实空间来探索那些我们所熟知的规则无法实现的“另类几何学”
在我们平时所学的一般几何学中, 两条平行线永远以相同的距离延续,从来不可能靠近或者远离对方。然而在非欧几里得几何中,同样的平行线最终会相交,或者改变方向渐渐远离。

佐治亚理工学院的Eilsabetta Matsumato与俄克拉荷马州立大学的Henry Segerman日前正在研究一个叫做“双曲VR”的项目,该项目旨在共同努力来向大众科普双曲几何学——一种两条平行线可以渐渐发散的非欧空间。Elisabetta Matsumato说:“你当然可以想象出这种现象,但是你很难切身感知它,直到你真正体验到了这种情况。”
在现在已经创造出的双曲世界中,使用者们除了四处走动以外,并没有太多可做的事。但是该团队正在计划在虚拟现实世界中创造双曲房屋以及街道,甚至建造一个非欧几里得版本的篮球。

在非欧空间中做体育运动并非一个新生事物,先前已经有一位伊利诺伊大学芝加哥分校的拓扑学家David Dumas在学生的帮助下制造了一个虚拟现实(VR) 壁球游戏。在此游戏中,在撞向不同的方向后球可以返回起始点。
Dumas说:“解决如何使用虚拟现实(VR) 作为一种研究工具现在才刚刚起步。”运用数学原理的可视化一直帮助良多,比如使用分形的视觉实现使人更好地理解潜在的数学世界。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

原文作者:Rebecca Hills-Duty。
译文作者:Jessie仪,哆嗒数学网翻译组成员,就读于布里斯托大学。
原文作者:Atheeta Ching,伦敦大学学院数理生态学博士。
译文作者:radium,哆嗒数学网翻译组成员。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
编者按: 有一个故事,说下雨天,大家都拼命的在雨中跑。有一个人却慢慢的走,别人问他为何不跑,他说,你没看见前面也在下雨吗,跑有用吗?很多人都是把这人当笑话来看的,但是这篇文章告诉你,问题没那么简单!
很多事情都影响着我们的生活,其中一件事便是天气,特别是下雨天未带伞(或者我们懒于将伞从包里拿出来)时的窘迫。凭直觉就知道似乎奔跑就是最好的选择,或者至少我们走快一点,就可以少淋一些雨。但是这也意味着雨点会以更快的频率从正面打在我们身上。
所以,如何才能让雨点在我们衣服上画的地图的面积少一点呢?这个问题实际上在过去的几十年里被众多的专家或爱好者们讨论过,无论是数学杂志还是像《流言终结者》这样的科普电视节目(事实上他们关于这个问题做了两期节目,第二期是对它的更正)。
让我们从最简单的模型开始,想象雨点匀速竖直落下。在图中,你就是那个灰色的长方形(因为下雨让你的心情不好,灰色可以表达这点心情)。
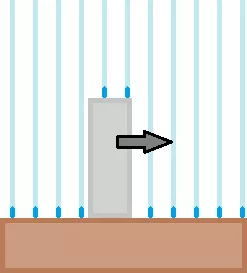
同时我们也要假设雨点均匀降落,其次第二个假设是假设雨点只从人的头上落下,而不考虑打在身上的情况。在这种情况下,无论雨点下落的速度有多快,你最好的选择便是“跑”。跑的越快你在雨中所淋到的雨越少。
好了,现在我们考虑,如果雨点因为风的缘故以一个角度降落在你身上又会如何呢?对于这个问题我们将会介绍一些真正的数学。和前面一样,我们将假设雨速度为定值Vr均匀下落。
雨域是这个问题的一个很重要的概念。这个区域包含了所有将会淋到你身上的雨点的初始位置。假设你以s的速度运动,因此在二维图上你的速度可以表示为向量Vu=(s,0),这使得你在雨中花费的时间为1/s。
在你身上取一个点P,在雨域取一点Q,在t时刻后在这一点上的雨点会淋到你身上。然后我们就可以得出出雨点会在Q + Vr·t这一点上淋在你身上。而你的原始位置P可以表示成为 P=Q + Vr·t − Vt·t。从而对于每一个你暴露在外可以淋到雨的位置P,对任意时间t∈[0,1/s],点P+(Vr−Vt)·t在雨域内.
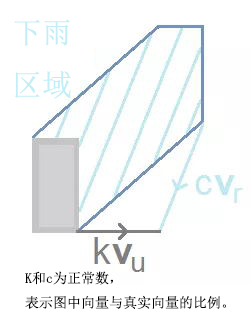
完整的下雨的区域由这些斜线勾勒出来了。每一条斜线的长度为 ||Vr−Vt||/s。这样就十分清晰了:如果雨以一定的角度下落,你应该跑的越快越好,缩短雨域的水平长度(下雨区域内的“宽”是定值,而和人的身高成比例)。
要是雨从你背后方来,又会怎样呢?这样一来,事情变得有一点复杂。雨点速度的分解为Vr=(V1,V2),因为雨点有向前方的速度,因此 V1>0。于是一些不同事情将会发生(假设雨以一定的速度均匀下落)。之前我们提到,你以速度s移动。如果s>V1你就不会被你背后的雨淋到,但是你的头部和你身体的正前方会被淋到。
如果 s=V1,也就是说,你的速度和雨在你前进方向的速度一样,那么仅仅只有你的头部会被淋到雨。最后,如果s<V1显然你的背部和头部会被淋到雨,但是你的身体的正面会保持干燥。令Af为你身体正面或背面的暴露在雨中的面积,而At为你头部暴露在雨中的面积。
在我们之前的二维案例中,这些只是表示你所代表的长方形的高度和宽度。雨点淋湿的这些部分的总量分别正比于Rf =|V1−s|·Af 以及 Rt=|V2|·At。
上述中在雨中的时间为1/s,被雨淋湿的函数为R,正比于:
R1(s) = [(V1 - s)·Af + |V2|·At]/s 若 s≤V1
R2(s) = [(s- V1)·Af + |V2|·At]/s 若 s>V1
其中比例的乘子是雨的密度。注意这个函数可以被应用到之前的例子。即雨点向后方下落,V1<0。我们发现我们总会有R=R2,因此让R最小化的方法便是尽可能地增加s。
雨点向前落下的例子中我们有V1>0. 让C = -V1·Af + |V2|·At 然后注意到R是连续的R1是一个关于s的减函数,而R2的变化依赖于C的正负。
如果C>0,R2也是关于s的减函数,要取R的最小值,那么s应该增加到最大值。
如果C=0,R2是一个常值。我们可以通过取任意的s≥V1来最小化R
如果 C<0,R2是一个关于s的增函数,那么我们仅仅只能通过让s=V1来最小化R。例如:你精确地于雨水平分量相同的速度奔跑。
C依赖于你的体格和在雨中的速度。如果雨向前方的速度很小,那么你最佳的选择任然是尽可能快的跑。但是,如果雨向前的速度很大,使得C<0,那么你最好精确地于雨水平分量相同的速度奔跑。同时也意味着雨点会打湿你的头部,但这些都是理论上讲的情况。
关于这个问题还有很多复杂的模型,考虑不同的形状(不是正方形的情况下)或者突然来阵一阵大风,都会影响最终的结论。最后,我们将以Matthew Wright(很遗憾不是之前Chalkdust的成员)写的五行打油诗来结束。
固执的青春
暴露在雨中的执拗
若雨从背后拥抱
我我便与雨同行
但若迎风而行
最华丽的步调
便是与雨赛跑
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
2011年3月11号日本发生9.0大地震发生,这次大地震震中位于日本的一个港口,它也让整个世界包括很多地震专家们感到震惊。它猛力地提醒着我们对断层以及它们突发的和灾难性的行为是多么的无知。如何找到断层清晰准确的几何描述并测绘出周围区域存在的拉紧形变区,这依然是一个悬而未决具有挑战性的问题。如果我们能克服这个挑战,我们就能进行地震活动的模拟仿真,进而更好的评估它对指定区域所带来的的风险。
我的合作者是约内斯库(他在巴黎大学),根据切向位错原理,我们已经开发出了一套行之有效的方法来定位和描述活跃的断层。这套方法是基于如下的假设:只有表面观察结果可以获取并且无牵引的情况可以应用于该表面。
我们也根据GPS的观察结果探索了探测慢滑移事件(比如无声地震或者地震成核阶段)的可能性。我们的研究依赖于对于已观察到的表面位移的渐进估计。这种估计在导出我们称之为矩重建方法的过程中被首次使用。之后它也用于寻找地表面移场必要的条件。这些条件就导致了以下两个参数的引入:活化因子和置信指标。根据表面观察结果,这两个参数可以用有效的方法计算出来。它们表明了一个标准変位场的产生是否是归因于活跃的断层。
结合最小二乘最小化和矩方法,我们之后发展了一个综合的断层轮廓重建技术。我们仔细研究者我们的重建工作是如何受到观测仪器敏感性和地表观测点坐标方格的步长的影响得。计算这样坐标方格最大的允许步长是为了应用于不同的断层深度和方向。最后我们得到了基于虚拟数据的数值重建法。
对于这种准静态断层滑动问题的正逆性的数学分析现在已经完备了。我们当前在应用这种理论来记录在太平洋海岸的墨西哥附近的大型区域测量的移位数据。这的确是一项很有挑战性的工作,因为我们不得不应对有噪声且有错误的数据,有时用那种花费极高的仪器一个月才解决几毫米的位移测量,这样只能得到极其稀疏的数据。在墨西哥沉没地区,一个可靠的活跃断层的重建只有通过各种数学模型的结合才能实现,这些数学模型要合理地反映压力,地壳移位以及待恢复参数的指定物理界限。幸亏有两个世纪的观察调查工作,地球物理学家们可以知道这些界限。
所以有没有那么一天地球物理学家能够预测地震事件呢?不幸的是,地震预测可能永远不会像天气预测那样靠谱。最多可能有一天我们能更好地评估一下一个地区在接下来100年内会发生地震的可能性。那就是说,知晓断层和给定区域应力剖面的精确几何形状可能会对于我们预测地震事件的强度和震波形式有所帮助。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

原文作者:RICHARD SANDOMIR,纽约时报记者。
译文作者:mathyrl,哆嗒数学网翻译组成员。
校对:donkeycn
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
新浪微博:http://weibo.com/duodaa
雷蒙德·斯穆里安(Raymond Smullyan),他的快乐,敏捷的头脑使他成为一个音乐家,魔术师,数学家,最妙的是,他还是一个创作谜题的逻辑学家(哆嗒小编注:实际上他的头衔里还有哲学家和道教学家),2017年2月6日(星期一)在纽约州哈德逊市去世,享年97岁。
他的亲人黛博拉·斯穆里安(Deborah Smullyan)确认了他的死讯。

斯穆里安教授是一名正儿八经的数学家,他的出版物和博士学位证明了这一点。但他最伟大的遗产可能是他设计的极其烧脑的逻辑谜题,它们或呈现在许多书籍中,或者只是出现在休闲的谈话中。
有时他们是一次性的,有时他们被嵌入更长的叙述中来解释数学概念,例如布尔逻辑,就像2015年他在《乔治·B的魔法花园和其他逻辑谜题》(The Magic Garden of George B and Other Logic Puzzles)中所做的那样;或者回溯分析,1981年他在《阿拉伯骑士的象棋奥秘》(he Chess Mysteries of the Arabian Knights)中进行了探讨。
他也是一个有趣的人。斯穆里安教授有着长长的白头发和胡子,长得像《指环王》系列电影中伊恩·麦凯伦(Ian McKellen)饰演的法师甘道夫(Gandalf)。他身材瘦长,讨厌健身,酷爱牛排和鸡蛋。他研究东方宗教。他讲老套的笑话,对身边的人表演近距离魔术。直到90多岁他仍带着激情和才华弹钢琴。 (尽管他年轻时因肌腱炎而脱离音乐事业。)
他对他自己的哲学、谚语情有独钟,例如,“我为什么要担心死亡?这不可能在我活着的时候发生!“
纽约城市大学研究生中心(Graduate Center of the City University of New York)的数学、哲学与计算机科学退休教授梅尔文·费廷(Melvin Fitting)回忆了斯穆里安教授的风采,在20世纪60年代,斯穆里安教授在叶史瓦大学(Yeshiva University)是费廷的老师,而费廷当时正在攻读博士学位。
教授在一次采访中说道:“他会微笑着期待他将要展示的许多美丽的东西。”
几十年来,斯穆里安教授似乎不停地创作的谜题,从中看到数学之美,并将其视为传播数学福音的工具。在他1982年的书《‘女士还是老虎?’以及其他逻辑谜题》(The Lady or the Tiger? And Other Logic Puzzles)中,他写道,如果希腊数学家将其作为一本谜题书,欧几里德的《几何原本》将会获得更大的普及。
他写道:“问题:给定一个等腰三角形,对应的两个角是否必然相等?为什么相等或者为什么不相等?”
他的谜题几乎是他本身的一部分,他与后来成为的妻子布兰奇(Blanche de Grab)第一次约会的时候就提出了一个谜题。
他向她提出的命题,就像他所描述的那样,一定能得到她的吻。回想起这件事,他写道,这是一个“赢得一个吻的相当狡猾的方式,不是吗?”
哆嗒小编插播:这是一个在数学圈流传很广的美谈。斯穆里安第一次见到女神时,达成一个约定——斯穆里安说一句话,如果这句话是对的,女神要给斯穆里安一张女神的照片,如果是错的则不给照片。斯穆里安说的话是:“你既不会给我你的照片,也不会亲我一下”。于是斯穆里安成功的获得女神的一个吻。
詹姆斯·麦迪逊大学(James Madison University)的数学教授杰森·罗森豪斯(Jason Rosenhouse),他在2015年编辑了一本书,书中赞美斯穆里安先生,对于那些以前不了解数学的人,他的谜题可以清晰地揭示数学之美。
“就像哄小孩子吃蔬菜,” 罗森豪斯教授在接受电话采访时补充说:“雷蒙德用一串逻辑谜题作为工具来展现诸如哥德尔不完备定理。“
马丁·加德纳(Martin Gardner),一位著名的数学谜题作者,把斯穆里安教授与牛津大学逻辑学家查尔斯·道奇森(Charles Dodgson)相提并论,道奇森也是以笔名路易斯·卡罗(Lewis Carroll)而更广为人知的作家。斯穆里安教授在1982年的书《爱丽丝漫游谜题王国:一个给八十岁以下儿童的卡罗式的故事》(Alice in Puzzle-Land: A Carrollian Tale for Children Under Eighty)中向卡罗致敬。
在其中一章,斯穆里安教授写道:爱丽丝心中思忖这个蛋人(Humpty Dumpty)是多么的混乱,但又相当合乎逻辑。
“我想知道,”她说,“他怎么做到既混乱又合乎逻辑的?”
在斯穆里安先生曲折的人生道路上,似乎有过一些令人困惑的逻辑。
雷蒙德·梅里尔·斯穆里安于1919年5月25日在皇后区法洛克威(Far Rockaway,Queens)出生,他的父亲伊西多尔(Isidore)是一名商人;他的母亲露西娜·弗里曼(Rosina Freeman)是一位家庭主妇。
他的求学经历是到处游学和不拘一格的。他曾就读于俄勒冈州的太平洋大学(Pacific University)和里德学院(Reed College),然后自己研究数学和逻辑。他还学习魔术。他创作了一些国际象棋谜题,这些谜题更为关注已经走出的棋步而不是将要走的棋步。
他以艺名Five-Ace Merrill在夜总会表演魔术,比如芝加哥Pump Room夜总会,他在那里工作获取报酬。他继续攻读并取得芝加哥大学的数学学士学位和普林斯顿大学的博士学位。他分别在普林斯顿大学、叶史瓦大学、纽约市立大学莱曼学院和印第安纳大学任教。
他的教学理念有点令人困惑。“我的原则是教给学生尽可能多的东西,并尽可能少地要求他们”,他对2008年的《Mathematical People: Profiles and Interviews》一书的作者Donald Albers和Gerald Alexanderson如是说。
但是,他补充说,明显的宽容所造成的影响是许多学生在他的课程中比在任何其他课程更努力。
斯穆里安教授身后遗下了继子杰克·科蒂克(Jack Kotik)、六位继孙子女和16位继曾孙子女。他的妻子布兰奇,比利时出生的钢琴家和音乐教育家,2006年去世。他的第一次婚姻以离婚结束。
科蒂克先生回忆说,他和妻子在纽约Elka Park的斯穆里安的房子里,听了有关职业运动员高薪的广播报道。他的母亲布兰奇说,他们的薪水过多了。
斯穆里安教授说,拿这么高薪水是不公平的。
“我说,‘雷蒙德,你比大多数人更聪明,不是吗?’”科蒂克先生在接受电话采访时说。 “‘是的,’他说。所以我说,'我认为这是不公平的。我们应该把你的大脑分出一部分分发给可以使用它的人。’”
“他沉默了一分钟,最后他说,‘我无法给出任何理由,但我不会这样做。’”
谜题是斯穆里安先生的一个重要组成部分 —— 逻辑学家打招呼和考验他人的方式。
当他遇到他最近的编辑罗歇尔·克伦泽克(Rochelle Kronzek)时,他要求她解答一些问题。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

“一开始吓到我了,但我想出了创造性的答案,”世界科学出版社执行编辑克伦泽克女士在接受采访时说,“他不止一次地笑了,因为他喜欢我的思考方式。看到别人如何思考,他从中得到很大的乐趣。”
原文作者:Gary Ernest Davis
译文作者:我是崔小白,哆嗒数学网翻译组成员。
校对:333
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
在经济、政治科学和心理学等社会科学领域中,人们普遍认为R = 0.7在线性回归的结果中是值得庆贺的。
R2 反映了因变量的全部变化能通过回归关系被自变量充分解释的比例,然而对于R = 0.7,这个比例大约是50%。
在物理学中,因变量和自变量需要更高的线性拟合度,所以在物理学期刊中,如果R2的值如果小于0.95则认为研究结果是十分不可靠的。
如果我们线性回归中的r2 =0.99说明总体结果良好,对吗?我们可以确定一定以及肯定,因为在因变量的变化中只有1%不能由自变量的变化来解释的。
其实那可不一定,可以用如下简单的例子来解释。
支原体细菌有一个包含580076个核苷酸的基因组。在该基因组中,起始密码子ATG出现了9,020次,并且这些ATG密码子开始和结束的位置为214, 263, 355, 452, 467, 547, 568, 686, 734, 822, 831, 850, 930, 1023, … , 579349, 579358, 579437, 579508, 579579, 579717, 579804, 579846, 579889, 579892, 579927, 579961, 580026, 580042。我们可能会问的一个问题是:这些ATG密码子的位置是否均匀分布在基因组上?
解决这个问题的一个非常简单的方法是,在1到580,076的范围内,产生9020个均匀分布的随机整数,并以这些随机整数为自变量绘制出ATG密码子位置的散点图。换句话说,通过线性回归,我们来看ATG位置的变化有多少是可以由均匀随机整数变量的变化来解释的。
(熟悉线性回归的读者可能会认为这并不是一个好主意,因为这里的自变量是服从均匀分布的,而不是正态分布——这是线性回归的基本假设之一。)
下面这幅图描绘的是ATG密码子的位置比照从小到大排列的9020个均匀分布随机整数的散点图:
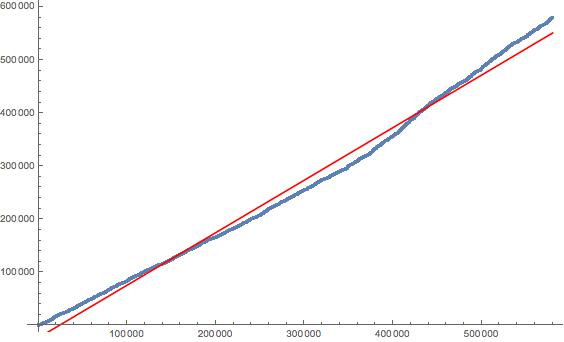
数据点的位置––ATG比照有序的随机整数–是蓝色的线表示,而回归线由红色的线表示。
对于这个回归得到r2 = 0.9912,这表明ATG密码子位置的变化只有小于1%的比例不能由自变量,即这里的随机整数的变化所反映。
然而,这幅图还告诉了我们一些别的东西:数据点先是在回归线的上方,然后落到回归线以下,接着又回到了回归线上方。
我们可以更清楚地了解数据点和回归线之间的差异–残差–通过观察残差图:
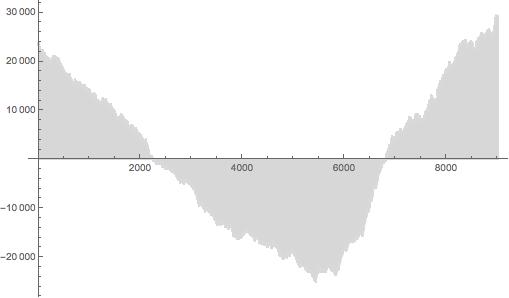
也许这只是一个从1到9020的特定随机选择的产物?
为了测试这个问题,我们可以多次重复我们的随机选择。当我们这样做的时候,发现这种模式仍然存在:在支原体基因组中,ATG密码子的位置和1至9020的有序随机整数之间存在很小但真实存在的差异。
基因组中的ATG密码子位置和随机位置是一个很小的但也可能很显著的差异。
作为一个生物学家,你不想深入研究一下吗?
警惕“高”的R2 值:仔细地观察回归中的残差图,并试图理解这个图背后的含义。
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文

微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
作者:王浩,牛津大学教育学硕士,香港城市大学英语博士,现于香港浸会大学从事英语教学工作。



| 分类 | 出现次数 |
| 数学论证 | 158 |
| 元数学论证 | 81 |
| 说明性结构 | 35 |
| 命题式展开 | 75 |
| 格式讨论 | 177 |
| 运营讨论 | 120 |
| 总数 | 646 |


微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
根据国际数学奥林匹克竞赛(IMO)官网最新消息(http://www.imo-official.org/),在巴西举办2017年第58届国际数学奥林匹克竞赛成绩揭晓。韩国队以170分的成绩获得团体第一,中国对159分夺得第二,越南155分获得第三。此前连续两年夺得第一,此次比赛志在三连冠的美国队,仅获得第四名。第五到第十名依次是,伊朗、日本、泰国、新加坡、中国台湾、英国、俄罗斯。

此次是韩国是第二次获得国际数学奥林匹克竞赛团体第一。2014年当韩国举办世界数学家大会(四年一届的数学界最高规格会议)时,第2012年韩国夺得的IMO团体第一被作为韩国当代的数学教育成绩被做入大会举办方的宣传视频。

此前,我们哆嗒数学网的小编介绍过此次比赛的一道题目(见这里)。从结果来看,这道和游戏有关的题目成为了此次比赛的最难的一道题目。来自111个国家的615名参赛选手,只有来自6个国家的7名选手有得分。其中,完全作对的只有来自俄罗斯和奥地利的两名选手。
近年来,国内在为“奥数”降温的同时,似乎部分舆论又在走向另外一个打压“奥数”的极端。相反,其他国家对“奥数”开始重视,比如美国的启动的集训模式,以及韩国的国家理科班模式。
尽管没有夺得第一名,第二名也是一个非常优异的成绩,我们向中国队表示祝贺!
微信、手机QQ搜索关注 哆嗒数学网 每获得更多数学趣文
