北京大学2019数学专业数学分析试题及参考答案
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa



















关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa




















关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
每年年底,美国数学会一如既往的在其网站上贴出过去一年的媒体热门事件。当然,这些事件是否热门,是从美国人视角看的。我们来看看,都有哪些吧。
以下内容改编至美国数学会的官网。
2018菲尔兹奖颁布
2018年,被人们视为数学最高荣誉的菲尔兹奖发布,四位数学界的顶级专家获得次殊荣,他们是:
贝尔卡, 英国剑桥大学。
费加里, 瑞士苏黎世联邦理工学院
舒尔茨, 德国波恩大学
文特卡什, 美国纽约大学

本届大会出现一个花絮,贝尔卡的菲尔兹奖牌在获奖后几分钟之内被盗,大会紧急重制了一个奖牌,并重新颁奖。贝尔卡自嘲道:“我是唯一一个两次获得菲尔兹奖牌的数学家。”
数学与选区划分
格里蝾螈(Gerrymandering)指专对特定某方利益设计并划分后的选区的手段。今年美国的中期选举引发了关于格里蝾螈的数学讨论。
甲壳虫乐队的歌是谁写的
喜欢摇滚的粉丝没有不知道甲壳虫的。甲壳虫乐队这地球上最成功的摇滚乐队之一。在某个夜晚,来自达尔豪斯大学的数学家詹森·布朗、哈佛大学的统计学家杰克·格里克曼前哈佛大学统计专业学生瑞安·宋,几位数学师生一起拆解了1963年到1966年甲壳虫乐队写的70多首歌——而且是用五种不同办法拆解。他们利用算法算出了,乐队成员约翰·列侬、保罗·麦卡特尼写出某些歌的概率。

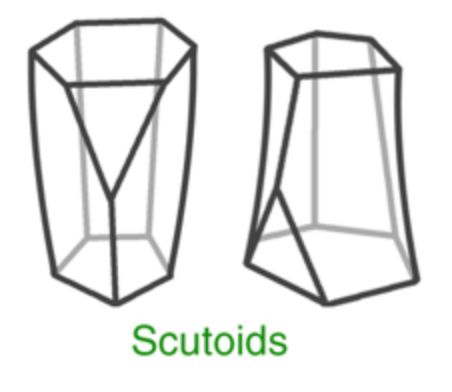
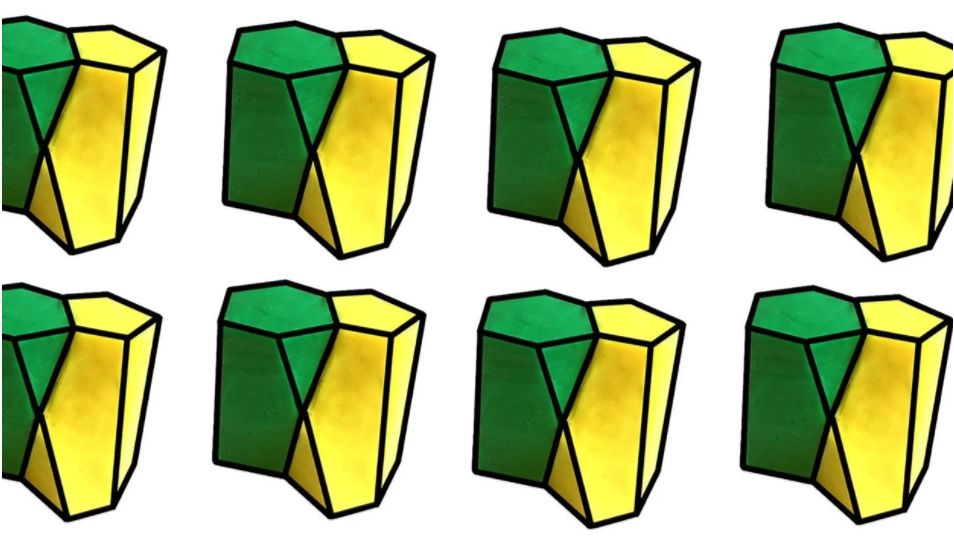
新的三维形状扭曲棱柱
发表在《自然通讯》(Nature Communications)上的一篇研究显示,科学家发现了一个此前在几何学中或尚未被定义过的三维形状,扭曲棱柱(scutoid)。利用此形状,可解释大自然如何有效地将细胞包装成三维结构。此消息被各个科技媒体广泛报道。
谷歌庆祝高斯的诞辰
传奇数学家高斯上了谷歌搜索引擎的首页,这回是为了纪念他241周年诞辰。记住是4月30日!
如何掰断一根干挂面条
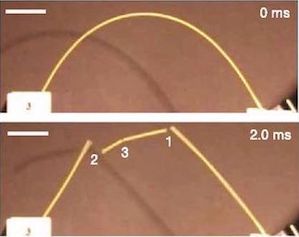
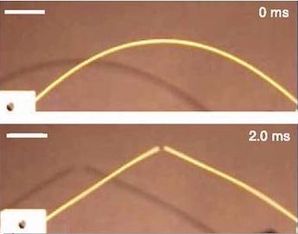
你有没有思考过这样一个问题。你拿着一根干的挂面条的两端,慢慢的掰弯它,直到掰断。这个面条为什么总是断成两截、三截,很少恰好是两截的。科学家们利用数学发现了如何确保断成两截的办法,并写成论文,发在四大名刊之一的《美国科学院院报》上(PNAS, Proceedings of the National Academy of Sciences)。
最大的素数
人类已知的最大素数的记录在2018年1月被刷新,这个素数有2300多万位,比上一记录多了100多万位。

数学家维拉尼的政治家生活
维拉尼是2010年菲尔兹奖得主。2017年,这位顶级数学家当选法国议员,开始了其政治家的生涯。我们哆嗒数学网的小编提醒你,2018年1月,法国总统访华的时候,维拉尼就如影随形,其夸张的装束,抢了不少镜头。

聚焦数学学科中的女性
今年,人们对女性在数学这一门学科的表现更加关注。在今年2018年国际数学家大会召开前,举办了第一届世界数学女性会议(World Meeting for Women in Mathematics,简称(WM)²)。
另外,不断有当代以及历史上的女性数学家的故事见诸媒体,其中有卡瑟琳·约翰逊、诺特、阿涅西、勒芙蕾丝伯爵夫人等。

如何将沙发搬上楼
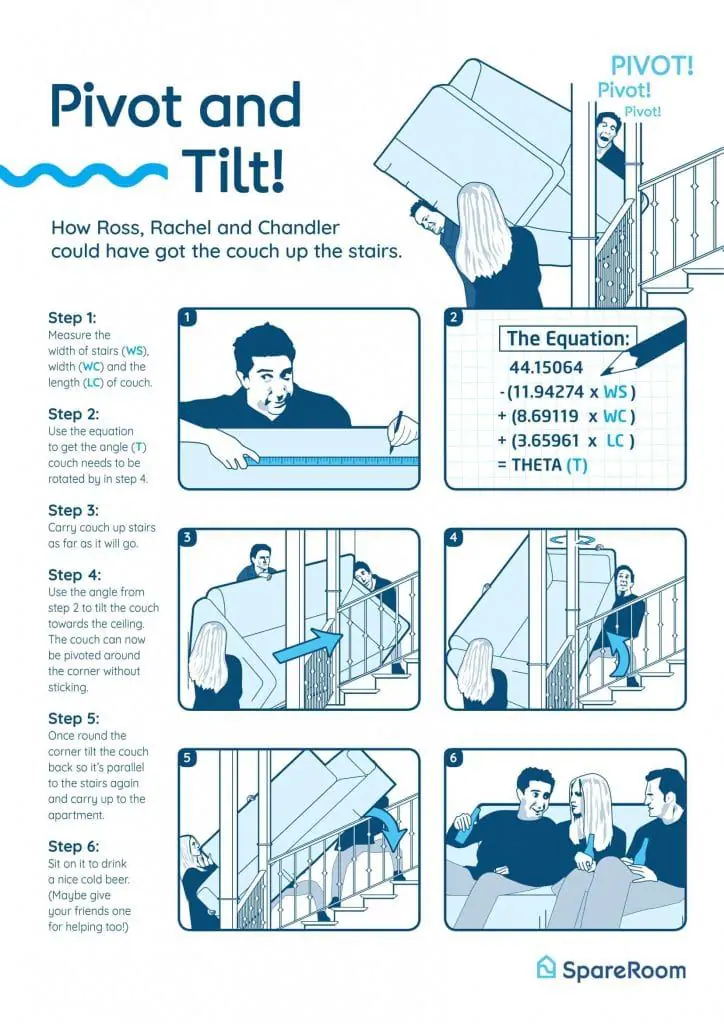
美国的一个情景喜剧系列表演了一个利用搬沙发引发的爆笑故事。于是,针对这个的讨论在网上开始了。搬沙发问题背后其实蕴藏着数学。每到毕业季,搬家旺季,是利用这科普数学的好机会!
数学继续助力前沿医学研究
用数学进行医学研究的现象已经越来越多。本年度,关于用数学对抗癌症,用数学解释疫苗的防病机制,用数学建模细菌相互作用等相关文章引起广泛讨论。
π和圆周率数学节
每年3月14日已经成为数学粉丝们的固定节日了。这一天,连必胜客、麦当劳都会在这一天开展专属活动庆祝π节。当然也受到了各个媒体的关注。

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
阿里巴巴全球数学竞赛已经结束,组委会要求题目的出题人对各自负责的题目进行了点评。很多点评非常精彩,哆嗒数学网与大家分享一下。当然,没有下面的张益唐教授的点评——张教授会出现在最后决赛选拔出的大师班里当导师。
温馨提示,点开图片看大图,清晰版本可缩放。

数论与代数方向命题人之一,Mihăilescu教授的点评:
(原文是英文,哆嗒数学网Math001翻译,Donkeycn校对)
1、 这些题目背后涉及了哪些经典的数学知识?试图考察考生哪些⽅⾯的能⼒?
如果来说我出的这几道题目,除了一道题目外全是数论题目。我之前没注意到,这份试题还包括代数。出题时,我遵循了以下这些标准。
第一,我意识到一道题目要成为好题目必须能激发答题者的思考,包括好的数感、思考方向以及通俗易懂的想法,不能仅仅只是基础的书本知识。由于这个原因,如果仅仅只是基于代数中的一些经典结构或者数论中的经典技巧,从而一眼就能看出解题方法的,我会尽量避免。
我同样注意到另外一件至关重要的事情,就是只有准确的审题和正确的解题思路并不意味着题目的解决。这和我们的现实生活一样,很多时候,没有思路想法,你什么都做不了。但极少时候,你拥有一个想法的同时问题就解决了。我们还必须正确和专业地完成一些技术性的具体操作:这些工作没有创新性,但需要你的专业性和专注力。比如,挑选了一道看上去像丢番图问题的题目,但如果答题者能很快看出背后蕴藏的数域,用一些基础概念甚至都不怎么计算就得到答案——这对于一个好问题的评判是一个减分项。
最后,这些标准必须符合足够竞赛性标准,就是说,预估一下思考解题思路时间,技术操作的时间,实际考试中大概至少最好的前20%的考生能很好地完成题目。除了个别难题外,其它题目一定不要太难,也不能计算量过大。平衡这些标准需要一些尝试——我没有受过出试题的培训,当然,我出的这些题目来自我的讲座。
回到我出的题目:其中一道题目需要知道p-分圆域的基本概念,这是数论基础课程中的关于数域的初等例子。需要利用一些熟练的计算以及一些好的思路来构造你想要的矛盾。另外一个题目需要知道更多数域概念和应用技巧,需要把代数数论的导引课程中的三个不同章节的知识串联起来来完成题目。第三个题目需要知道一些p进数分析的知识,这大概是我出的最难的题目。但总的来说,所有这些题目,优秀的本科生都应该能作出解答。如果一位本科生认真地上完基础课程,然后稍稍向课外扩展学习一部分,都应该能做出来。
2、 决赛的出题思路和其他类似的数学竞赛有什么不同?比如和普南特数学竞赛、国际大学生数学竞赛(IMC),丘成桐大学生数学竞赛等赛事有什么不同?
这个问题我回答不了,我就只是出了三道题目。其他的不了解,无法评价。
3、 阿里⼤师班希望从决赛中选拔出什么样的⼈才?
回答第一个问题的时候,我已经表达了——解决题目需要思路与具体操作相结合,在数学中那个两者都很重要,缺一不可。无论你做什么,你需要思路,也同样需要具体技术和熟练度来实现你的想法。在高级课程中当然会优先挑选这样的人才。
4、 每道题目你花多少时间来出题,出题的时候你怎么考虑的?这些题目和你日常研究有关系吗?你怎么想出这些题目的?
非常不一样。总体来说,讲真,题目创作我大致用了一周时间,寻找题目的解题思路,不断打磨题目,使他们成为一个合适的竞赛题目。然后,在某个晚上,我把答案写了出来。
是的,题目和我的日常研究多少有些关系。我对自己的要求是,这些题目不能是某些教材和论文上题目原题或变形,毫不夸张的说,这些题目是原创的,有些思路一些同事在讨论的时候还很惊奇,居然这样也行。关于科研是这样的,当你全情投入的时候,原本的问题会派生成大量的相关问题,这些问题的答案对你的工作没有直接用处,但对问题更好的理解很重要。考试的时候,当你思考到能解决试题的时候,这种行为就需要被打断了。必须记住,一个人必须能够在一个小时内完成解答——而且有三分之一到一半的时间是在得到思路。
5、 进入决赛名单中有六分之一的人是已经毕业参加⼯作并且不再学习数学的⼈,如何看待并评价这一现象?你有何想法?(他们能解答你出的问题吗?他们适合做这些题目吗?)
对于这个问题不想说太多——为什么这些考生要特殊看待?他们了解这个考试是什么水平的,他们是被数学吸引来的,否则他们不会来参加,所以这不是问题。我觉得他们不必是做数学科研的!这样说不定还有小优势.他们依旧得回去工作,只是这里有更好的机会。
6、 这些题目对我们的日常生活有用吗?或者对我们生活中做决策有帮助吗?(更宽泛的,你可以谈谈你想谈的。)
是的,这是一个老生常谈的问题:我们为什么做数学。一些数学家经常反问:“为什么我们需要音乐?”,这也是一个聪明的回答。最近的研究表明,音乐对健康有诸多好处。排开这些,除了兴趣爱好和带来愉悦,音乐还有别的用处吗?对于数学以及精确表述事物的能力,我们通过训练如何提问来培养人们精确表述问题的能力。这些能力在诸多场景下,都非常有价值。但不是直接的价值,就像心法,只是一种能力。
假设你现在在接受一位最优秀的滑雪教练的关于滑雪的身体素质训练(译者注:和组委会核对,原文sky是笔误,应该是ski)。你充满动力,而且很好的完成了训练任务。但是,你家离最近的滑雪场也有2000英里远,你既没有钱也没有时间去进行一次真正的滑雪。那么这些滑雪训练对于你的人生是有用的吗?因为可能无法验证,你无法知道答案。虽然,在某个合适的时机,这些训练会派上大用场——毕竟,是一位优秀的教练教的——但是,仅仅是训练和实际上场区别是很大的。人们会说,当你上场的时候,你的大脑和身体必须在实战环境中做反应,你需要把练习中得到的经验与技能与实战环境联系起来。这其实是另外一种能力,一些人能很轻松的把理论知识和模拟练习的要点和实际操作联系起来,能很快提升。而另一些人,即便在训练中很得心应手,进入实战的时候也不顺利。这的确是事实。我认为,之所以造成这样的结果,原因是一些人在练习时,太聚焦于练习本身,只学习了刚好能完成练习的最浅显的知识。而另外一部分人从来不忘初心,当他们做练习的时候,永远把自己的目的放在心中最重要的位置。做到后者的确更难,但是却能将知识与实践更好地结合。而前者那些人迟早会遇到阻碍,因为实际情况永远不会的和练习时模拟情况百分百的一致,当遇到和练习时不同的情形而需要调整技巧的时候,这些人就可能遇到无法逾越的障碍。如果一直牢记这种与现实的联系,才能在遇到特殊情况时,有效的运用自己之前学到的东西。
从这个意义来说,我认为,做练习对日常生活是大有用处的。
如果可以的话,我也有一个问题。询问一些题目出题过程的背景和目的是什么,我觉得对赛事本身的提高帮助不大啊。或者说,我这样问:我是不是误解或者曲解赛事的背景和目的?
数论与代数决赛题目:

几何与拓扑方向命题人之一,朱晨畅教授的点评:
1、 决赛试题的用通俗的语言体系来说,是一个什么样的水准,要用到什么阶段的数学知识;
决赛试题是需要大学一到四年级所修的专科数学知识的。然后需要有融会贯通,和较强的逻辑思维能力,以及一些创新的灵感。
2、 相比于初赛,选手答决赛阶段的题更需要用到什么样的能力和知识?
相比于初赛,选手答决赛阶段的题更需要一些近代的数学知识,例如群论,微分几何,拓扑,等等。这些都是近一两百年,甚至上个世纪develop的近代数学思想。
3、 这几道题目的含金量如何?能否具体解释下这些题目的含金量?命题组花了多长时间来出?
这些题目的含金量是相当高的,就几何拓扑这个方向而言,第一道题用到Hopf fibration, 三维球面的handle分解,以及三维球面与SO(3)的关系。第二道目也是用到拓扑里面相当经典的基础知识,像是Lefschetz duality, excision theorem, long exact sequence for relative homology, universal coefficients theorem。 将这样的经典几何或拓扑知识如此巧妙的结合起来,这两道题可谓处处是金点,但又特别自然。所以是两道又漂亮,又经典的好题。
整个出题的过程是,我们自己先分别出好题,原题往往是和我们自己的研究方向有关的。是我们在平时思考问题的一些积累。有的甚至还真的是我们平时研究的数学问题的一个小步骤呢。然后我们将原题送小组讨论,大家试着解对方的题,以考察难度系数。然后给对方一些建议或方向,怎么样提高或降低难度。而且实际上,我们是有更多的题目的,然后从中选出四道,也是横向和其他小组比较的结果。这前前后后,大概有一个月的时间。
4、网传聂子佩、王彬等大神来参与,他们具体牛在哪?有什么厉害之处?这次比赛大概吸引了多少这样的大神来参与?
我知道的还有国外的大神,比如说得到IMC特别一等奖,并之前三次参加IMO的一位欧洲选手(请保密,欧洲人对这种消息是很个人的看法的,如果要公开,我可以问问此人)。所以应该是高手云集吧。 打一个比方,这就好像是华山论剑,真正的高手是会忍不住去论一下的。据说习武之人,有一个比武/修行/传道的渐进过程。对数学感到强烈共鸣的人,也是一样。开始都有参赛解题的欲望,然后随之而来会有理论上的提升,以及之后的教书育人。不是所有IMO的金牌得主都会成为Fields奖获得者,但在Fields奖获得者中,很大比例的都曾经有不平凡的数学竞赛的经历。
以我个人在数学里的经历,每个人的灵性,直觉,反应的速度,解题的准确度,对问题的透视能力,都是不同的。那些大神们,比平常人这些能力会强,甚至强很多。这样的能力从参赛解题会很明确的反应出来,尤其是好的题目,漂亮的题目。这些能力,有一部分是天生的,然后个人的长期的努力和专注也是可以提高这些能力的。然后呢,解出一道题目的快感是很大的,然后横向的比较,或者在其他选手中讨论共同的题目的共鸣的快感也是很大的。这样的感觉甚至是超过文化和语言的。
以上也许就是这些大神牛的地方,也是为什么他们乐于参赛的原因吧。所以我觉得阿里的这个竞赛唤醒了,或者重新激发了这些对数学有共鸣的人。希望这样有天赋的同学们,可以进一步从竞赛到修行,有一个提升的过程。这也许就是阿里大师班的深刻用意了!
几何与拓扑方向命题人之一,某教授的点评。
问题:
这⼏道题背后涉及了哪些经典的数学知识?实际考察的是数学领域哪⽅⾯的能⼒?
决赛的出题思路和初赛以及其他数学⽐赛的有什么不同?
(决赛)⼤师班希望选拔出什么样的⼈才?
出题前后花了多长时间?是否有把⾃⼰平时研究的数学问题放到题⽬中?
初赛的⼊围名单中有六分之⼀是已经毕业参加⼯作的⼈,如何看待并评价这⼀现象?
决赛这些题⽬有可能怎样去指导我们的⽣活或者⼯作决策?
回答:
第一道题⽤用到Hopf fibration, 三维球⾯面的handle分解,以及三维球⾯面与SO(3)的关系。
第二道⽬目也是⽤用到拓拓扑⾥里里⾯面相当经典的基础知识,像是Lefschetz
duality, excision theorem, long exact sequence for relative homology, universal coefficients
theorem。 将这样的经典⼏几何或拓拓扑知识巧妙的结合起来,这是两道⼜又漂亮,⼜又经典的好题。
第三题,我们可以⽤用常微分⽅方程的知识放到manifold上来做⼀一些计算,相当于是⼏几何分析的⼊入⻔门功底。当然,也可以⽤用到⾟辛⼏几何中的Louville’s Theorem , 避开计算,直接得到结果。两种办法都是⾮常棒的。
第四题,看上去有⾮常浓厚的离散组合味道。后⾯还有⼀个⼩故事呢:出题委员会的⽼师刚刚出初版的时候啊,⼤家都很喜欢染⾊剖分的主意,觉得很新颖很漂亮很有数学竞赛的味道。开始给的答案需要⽤到relative simplicial approximation。于是⼤家就有了争论了。⼀部分⼈认为这个很⾃然,simplicial approximation⼤家都熟悉,那它relative的version应该可以想到也是对的,⾄少直觉上很快的。另⼀部分⼈认为是如果真的查⽂献呢,这个倒是⼀个冷门结
果,⼀般的拓扑书中倒是没有,⽽且考试也并⾮开卷,不能上⽹查⽂献。第⼀种情况更像是以做研究的⼼态去考察参赛者,⽽第⼆种考虑的确是更稳妥更周到⼀些。于是在⼤家的互相讨论互相解读中,慢慢修改,终于得到最后这⼀版,是可以⽤经典的拓扑知识逐步解决的。
整个出题的过程是,我们⾃⼰先分别出好题,原题往往是和我们⾃⼰的研究⽅向有关的。是我们在平时思考问题的⼀些积累。有的甚⾄还真的是我们平时研究的数学问题的⼀个⼩步骤呢。然后我们将原题送⼩组讨论,⼤家试着解对⽅的题,以考察难度系数。然后
给对⽅⼀些建议或⽅向,怎么样提⾼或降低难度。⽽且实际上,我们是有更多的题⽬的,然后从中选出四道,也是横向和其他⼩组⽐较的结果。这前前后后,⼤概有⼀个⽉的时间。整个合作的过程,我们感到还是很愉快的,同时也甚⾄进⼀步了解了⼩组成员的research。
最后,选出来的题⽬,考察了同学们的对经典⼏何拓扑知识的了解,以及融会贯通的能⼒。决赛的出题思路⽐起初赛,更加偏向于受过⼤学专业基础并有活跃创新意识的同学。这也是我们对⼤师班⼊选同学的期待吧。
当我们听说⼊围名单中有六分之⼀是已经毕业参加⼯作的朋友们,我们对此感到很⼗分感动的。想不到,有如此多的⼈们竟然对数学是如此热爱,即便是参加了于数学研究不直接相关的⼯作,仍然将这么多的时间和精⼒,投⼊数学。作为职业数学家,我们是知道只有⼀个⼈对数学有⼗分的热爱,才能够达到这份境界。因为这个基本上是与你的前途,提升,没什么直接关系的。决赛的题⽬呢,我们也于是希望做到,有⼤学知识就可以解出来,然后有⼀些相关的research经验的,可以看出其中的门道和含义来。
⾄于决赛的这些题⽬是怎么样有可能去指导我们的⽣活或⼯作决策吧,我们这个⼏何拓扑组的题⽬可能真的是没什么真的联系,可能第三题会帮助在现实⽣活中算⾯积的时候多⼀个思路,⽆论是在⼯程中还是物理⼒学中。但是我们敢肯定,能好好解出这些题⽬的⼊选者,⼀定有很强的逻辑思维能⼒,以及⼀定的灵性。这样的⼈才,⼀定不可多得!
几何与拓扑决赛题目:

应用与计算数学方向命题人之一,董彬教授的点评。
1、 决赛试题的用通俗的语言体系来说,是一个什么样的水准,要用到什么阶段的数学知识;
题目水平相当于美国top 20高校博士资格考的水平,需要用到高年级本科及低年级研究生课程的数学知识。
2、 相比于初赛,选手答决赛阶段的题更需要用到什么样的能力和知识?
决赛更多考验的是学生对数学知识的灵活掌握,弱化技巧,强调理解,对不同应用数学课程内容的融会贯通。
3、 这几道题目的含金量如何?能否具体解释下这些题目的含金量?命题组花了多长时间来出?(通俗的说,就是我们的题目出的好,好在哪里?)
前后我们经过近一周时间,思考和对试题进行讨论。我们的目标是考验学生是否能够跳出书本上的内容,会用所学到的数学知识来解释一些更偏应用的问题,真正体会数学的有用之处。这和目前所有同级别的数学竞赛都不一样。当然,这也给命题带来了很大难度和挑战。
4、 网传聂子佩、王彬等大神来参与,为什么我们能吸引到这些人参赛?
我想除了阿里巴巴的盛名以及高额的奖金,那就是试题的挑战吸引了众多大神来一决雌雄。
应用与计算数学决赛题目:



最后,附上分析与微分方程的题目。
分析与微分方程的决赛题目:

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa




关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
《世界奇妙物语》是日本的一部涵盖诸多元素的电视巨作。1990年开始播出,到今天都快30年了。在日本,一直有一群狂热的粉丝在追这部巨制。
除了正剧,《世界奇妙物语》还会拍摄特别篇。今天介绍的就是《世界奇妙物语》2018秋季特别篇之四——数学的傍晚!让我们感受一下,岛国娱乐圈是如何“吹”数学的奇妙的。
开头。
女主凛子是一位女学霸。一天,她骑车走在放学的路上。

突然,道路旁边窜出来一群不良少年,拦住了她,问她是不是学习好!受到惊吓的凛子只好承认!


不良少年们,终于暴露了他们的目的。他们拦截凛子的目的居然是,想知道什么是——同心圆。
……

于是,凛子只好就范,向他们解释同心圆是什么……


原来,这群不良少年有一段悲伤的过往故事……
这群不良少年本来是学校里的小混混。他们抽烟、酗酒、打架。而穿白衣的隆君就是他们的带头大哥。

他们感情深厚,情同手足。当然,作为学渣的他们,自然无法毕业,一直处于留级中……

但是,不知道怎么的,大哥隆君死了……

在悲痛之余,一个偶然的事情,让他们重燃的希望,他们见到一本记录能让人起死回生方法的黑魔法书。



但是,他们发现,根本看不懂,因为书上全是——数学!


于是,不良少年们请来凛子帮他解释书中内容。发现凛子还是懂不少的。

凛子向学渣们解释了什么是内接在圆内的五芒星……

然后,发现书中记录的居然是“鸡兔(猪)同笼”问题。



还有,浓度计算问题。


植树问题也出现了!


凛子发现要读懂这本魔法书,还需要微积分的知识。


凛子说,这超出自己的学力范围,也搞不定这本书。

搞不定的理由竟然是——自己是——文!科!生!(我们哆嗒数学网的小编不知道这样黑文科生好不好……)

没关系,不能放弃!
于是凛子向学渣们提出建议:“我们一起来学习吧!”

很快,他们知道了鸡兔同笼的数学本质。

解决了浓度计算问题后,他们懂得了为什么不要酗酒。




三角函数的知识让他们学会了走近路。他们更加理性,也不再打架。



当然,美好的爱情也如期而至!

连表白都用的数学!

他们的恋爱非常甜蜜,偶尔也会透着忧伤……



到了秋天,本来学渣的他们居然理解了微积分!

数学的学习让他们的命运也开始改变,原本根本不可能毕业的他们,居然被老师建议考大学!

但是,他们的初心一直没有改变——复活隆君。

他们成功了,隆君复活!

但是,复活后的隆君发现,世界不一样了!
他原来的好哥们儿不在抽烟,不再赌博……


——数学的力量真是神奇呢!
全剧不长,13分钟左右。
数学改变了男生们的心智,
数学改变了男生们的命运,
数学帮他找回了曾经被无度挥霍的青春,
数学还能给他们美美的爱情。
当隆君复活,复活的其实不是隆君本人,
而是当年的自己!
数学的熏陶,让他们彻底脱胎换骨!
他们毅然决然的抛弃了当年的自己,
从废柴成为顶天立地的好男人……
我们还有一个感受是:
原来我们的数学老师
一直对我们隐藏着天大的秘密!
多少年来,他们一直在传授我们黑魔法。
却一个字也不说……
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Kevin Hartnett,《量子》资深作者。
翻译作者,whymath,哆嗒数学网翻译组成员。
校对,333。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
背景
数学中大多数重要的发现要经过几十年或几个世纪的努力才能得到。如果你想要研究数学中最难的问题,就必须要掌握大量高专业性的知识,才能发表些新的看法。

数学家Richard Schwartz沉浸在他所发现的简单数学问题的奥秘中
而这些最难的问题没有引起理查德·施瓦茨(Richard Schwartz)的兴趣。他喜欢的那种可以今天读,明天着手解决的问题——简单的、有趣的、有些像游乐场游戏那种走一步看一步的问题。施瓦茨的这种性格在理论数学家中相当少见,他曾说:“我觉得自己对数学的态度是童真的”。
但这并不是说施瓦茨不是一个严肃和卓有成就的数学家。恰恰相反,他在近半个世纪来最重要的数学家之一——比尔·瑟斯顿(Bill Thurston)的指导下于普林斯顿大学获得了博士学位,现在他是布朗大学的终身教授,并在动力系统领域取得了他最重要的研究成果——研究迭代过程的长期表现,如一个台球在无摩擦桌面的跳动现象。2008年,他证明了每个内角都小于100度的三角形任意都包含至少一条台球路径——一个台球将在其上做周期性往返运动的路径(注: 想象在一个无摩擦的桌面击打一个台球,这样台球将不断碰到桌壁,然后反弹。假如过了几年再回来看,会发现什么?施瓦茨证明了这个台球将以行星绕太阳旋转般的方式在固定的轨道上做周期运动,而非不断产生新的路径)。
施瓦茨在其多数工作中都使用了计算机实验,可称得上是这方面的弄潮儿。正他说,计算机在好些方面对人类的数学思维形成了助力:计算机找到的模式给予了证明问题的启示,而这是很难单靠人脑想到的。
《量子》杂志对施瓦茨进行了访谈,访谈内容包括其本人对简单问题(他称之为“数学奇迹”)的喜好和他即将面世的关于无穷的儿童数学读物。以下是整理过的谈话内容。
您喜欢数学的什么?
我喜欢关于它的全部。当然了,我首要喜欢的是它有用。我喜欢它是流程化的这个事实,这让你总可以找到前进的方法。我喜欢它不像政治和宗教,在这些领域内的讨论多少年都不能改变对方的观点,而数学则可以探入到问题的最深处。
我还喜欢几何图形和数字,我对他们有着我所无法解释的原始的热爱。还有我也喜欢智力挑战,我喜欢解决问题,尤其是大家无法解决的那种——这有些像登山者的心理。最后,我还喜欢纯数学的美,就像有人喜欢艺术品一样。
您说您喜欢简单的问题,为什么?
我觉得如果一个简单的问题还没有被解决,那么这个问题一定还有隐藏的深度,即存在人们所意想不到的事情阻碍了问题的解决。
其次,我还喜欢做计算机实验,因此我时常感到我有在这种问题上取得进展的机会。现代计算机是一个新的工具,而这些简单问题也可以被视为数据(模式)搜索的渠道。比如,我正打算在计算机上编程并做一些实验,来发现那些隐藏的模式,以前这些模式没有被人发现,就是因为没有人做过这样的实验。
第三,我所喜欢的简单问题不需要太深的背景知识,可能听起来有些傻气,我喜欢那种我恰好可以介入的那种问题。我还很有耐心,如果听说一些流行数学领域的猜想,我不会予以理会,我不喜欢花上六个月的时间读文章,然后才能达到着手解决问题的地步。我喜欢接地气的,可以立刻开始的那种问题。
什么是简单问题?举个例字?
我非常感兴趣的问题之一就是三角台球问题。它是这样说的:观察一个三角形内的台球,是否存在一条周期性的台球路径,使得台球在这条路径上一遍又一遍的重复其运动轨迹?对锐角三角形来说答案是已知的,但对钝角三角形来说则不然。问题是:对于任意三角形来说,都存在这样的周期性台球路径么?我在这个问题上做了一些努力,证明了若三角形的内角均小于100度,则该路径存在。
可以请您再举一个例子么?
另一个我曾下了一些功夫才解决的是外台球问题。假设你有一个平面上的凸形,椭圆,正方形或五边形都可以。然后你就从凸形外一点,嗯,也许我该画个图来说明。
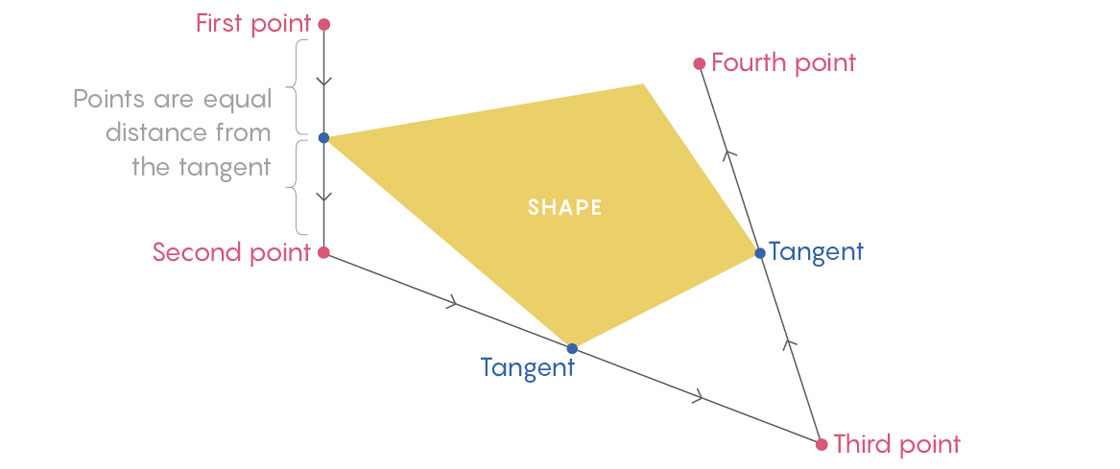
从凸形外的某个起始点(第一个点)开始,做凸形的一条切线(与凸形仅有一个交点的线),然后在离切点距离等于切点至起始点距离的地方停下来,这是第二个点。重复这个过程,最后由这些移动的点形成类似星体轨道的图形。
核心的问题就是:是否存在这样的凸形和起始点使得动点可任意的远离凸形?动点的运行轨道是否是无界的?我证明了对于某些特定的凸形,比如风筝,这种具有双侧对称性的四边形,动点将远离凸形。
请告诉我您是怎样在工作中使用计算机的,以及为什么您喜欢使用?
我首先要说的是,计算机是用来打草稿的利器。数学家,甚至伟大如高斯和欧拉,都曾致力于搜索实验证据。他们将在草稿纸上手算问题的特殊情况为自己提供关于结果的灵感。在某种意义上,你可以用电脑做很多类似的事,它让你搜索更多的关于可能的正确结果的实验证据。

朱利亚集可以显示为表示某个复杂函数行为的分形
计算机还是一种可视化的工具。它揭示了这样一件事:没有它的帮助你可能将无法得出正确的观点。一个真的要用到计算机的好例子是曼德布洛特集,不使用计算机,你当然可以徒手绘制出一系列的散点,而一旦使用计算机进行辅助,却能够揭示蕴含其中的丰富信息。没有大量的计算和绘图,曼德布洛特集,朱利亚集以及类似的事物将是不可能被看见的。
存在计算机解决不同本质的问题的方式么?
我只能说我个人认为,数学十分适用于高对称性的事物。从某种意义上说,数学几乎是奇迹。一个近期的大型的例子是玛丽娜·维娅佐夫斯卡(Maryna Viazovska)在八维空间给出的开普勒猜想(这个猜想就是球体最密堆积问题)的解。令人惊讶的是,开普勒猜想的解决在八维空间内要比在三维空间内容易得多。原因是这些神奇的球堆积在八维空间是极其、极其对称的,在八维空间内这样特殊的构造简直就是神迹,但若没有这些非同寻常的对称,从某种意义上说,问题就无从下手了。所以计算机在这里帮了大忙,因为它使你能够对所有的可能性进行遍历。
您说数学被有组织的用于寻找那些最对称或最美丽的事物,可以请您详细谈谈么?
这就像是数学行经这个世界时,毫不犹豫地拾起了最闪耀最美丽的宝石。譬如对数函数、零函数、指数函数,几何中则是线和面,最近的流形学中则是曲率空间和概型一类的奇怪的东西——我不大能理解这些东西。数学就是用在这些典型事物上的。你可以说这才是数学家们应该做的——寻找更多的类似的典型,更多的宝石。但回过头来说,这可能是那种初看起来十分难的不起眼的宝石。
那么计算机可以帮助找到这些不起眼的宝石吗?
当然能了,那是我从外台球问题得到的经验。一开始,外台球在一个风筝形的平面上产生的运动看起来完全是噪声,而且很难理解,我不断尝试使用不同的方式来表示数据,最后我想到了画出更高维度的数据表示,突然,我的眼前就出现了这个美丽的模式。我敢说,没有计算机的帮助,我永远都猜不到这个答案。
计算机可以搜集大量的信息,可以将事物图形化,可以作为你的外部存储空间,因此它可以帮助你识别那些太渺远以至于无法识别出来的基础模式。计算机是一条捷径,你可以在太多的地方用到它了。某种程度上,你甚至不需要花脑子想问题,至少一开始不用,然而你同样将得到计算机的反馈,然后你再根据这些反馈调整实验。并且假如你成功了,一定将发现单靠自身所无法找到的新知识。

Schwartz家中书房的分形时钟
您写了好几本儿童数学读物,您写作这些书籍的动力是什么?
原因有两个。我孩子还小的时候,我想要教他们数学。一开始,我为我的女儿露西写了一本薄的关于素数的书,但后来我沉迷于这件事无法自拔,写成了一本叫做《快来数怪兽》的完整的书。我的孩子是我莫大的动力,因为我总想要向他们解释这些整洁的东西。另一个原因是我喜欢画画,我画的不算太好,但我就是喜欢计算机绘图。嗯,就是这样。
数学之外,我喜欢的有创造性的东西,它们是我日常研究之外的小憩,我喜欢拥有大量的观众。像大多数数学家,我致力于研究的问题——即使这些问题被解决并且构成了另一个未解决问题的解——不太可能有好几百人愿意了解。而知道自己的图画书被好几千人阅读则是一件很值得高兴的事。
在数学上我投入了大量的脑力工作,我想知道,如果我在一些问题上工作地十分努力,而得到的成果只有很少的人将会看到,那么生命的意义何在?也许,撰写这些儿童读物会是我知道自己的研究成果正以正确的方式发挥作用的机会。
你正在写一本新的儿童读物《无穷农场上的生活》,你打算向孩子们传达关于无穷的什么呢?
在孩提时代,我曾想了很多关于无穷的事——如果我有无穷长的胳膊会怎样,如果桌子是无穷的又会怎样。我认为孩子们会喜欢的,无穷是一个有趣的概念。





Schwartz的第四本上市书籍《无穷农场》中的示例页面
关于无穷,有什么特别想要孩子们理解的东西吗?
第一件事就真的是对无穷的感觉了,无穷并不是一件东西。比如古典音乐,假如你从未听过古典音乐,你可能会想古典音乐就是音乐,但假如你有兴趣了解的话,你会知道音乐其实是巴洛克、古典、浪漫、现代——所有风格和乐器的组合。这个例子主要是为了让孩子们了解无穷的可能性,因为音乐是事物走向无穷的另一种方式。
还有另外一个实质性的部分,就是要让孩子们看到一些让人眼前一亮的真正激励他们的东西。孩子们在学校的学习通常枯燥无味,尤其在数学方面。知识通常没有被很好的传授,孩子们也经常被填鸭式地教育,那样的方式毫无生趣。所以我的想法是传达一些孩子们真正感兴趣的激励他们的东西。
你从事数学工作的30年来,对数学的理解有过改变么?
我不知道,某种意义上来说,我对于数学的态度并没有改变多少。我对高端的流行的数学从不感冒,比如朗兰兹计划或范畴论,这一点我从未改变。我认为我对数学的态度是童真的。我记得我在母校的时候还曾这样想:好像身处某个游乐场,你看到有很多不同的游戏,比如向可乐瓶子扔环套住它之类的,你似乎只需要做些游戏就能拿到你的博士学位。我一直没有什么大的研究项目,我仍然痴迷于这些奇怪的简单问题。
也许现在我越来越熟知的一件事就是人类的知识充满了漏洞。关于数学,年轻无畏的你认为万事尽在掌握,而我却感觉所知不过沧海一粟。人们如首尾相衔的蚁群般不断前行,所经过的轨迹窄小得可怜,轨迹外的世界就是未知的世界,这就是我越来越强烈的明悟。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Doug Lederman,《高等教育内幕》杂志创办人。
翻译作者,关小胖,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa


关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Natalie Wolchover,量子杂志资深作者。
翻译作者,柳北丁,哆嗒数学网翻译组成员。
校对,小米。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa


关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Enrico Degiuli。
翻译作者,溦之洸茫,哆嗒数学网翻译组成员。
校对,donkeycn。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

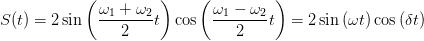
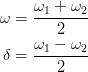
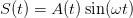
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa




作者,e^iπ+1=0
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa





关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
本来关于这个,在论文没有正式公布前,我们哆嗒数学网的小编本来什么都不想说,但不断有人“提醒”我们应该说一说——微信提醒、QQ提醒、各种私信提醒——于是我们还是说一说吧。
首先澄清,之前不在公众号发布这个消息,是因为这本来是别人小圈子的内部讨论班,该讨论班的参与和组织者并没有希望把此事在这个时候就变成公共事件。我们不报到也是因为不想影响当事人师生的正常教学授课秩序,与当事者的名气、国籍无关。这不,原定的的讨论班时间被一波莫名其妙的舆论搞得推迟了不是。
最新消息是,网传黎曼猜想的证明在10月13日由李忠教授在中科院数学所南楼某教室的讨论班上公布。这个消息被汤涛院士在他的微博“数学文化”上发布。我们也多方打探,这个讨论班的确存在过。


关于对定理猜想证明的态度,我们知道的有两种:
一是网传的郑忠国老师、彭立中老师两位北大数学教授对证明的肯定,认为李忠教授的确证明了黎曼猜想。
另外一种就说得比较婉转:“李教授和阿蒂亚爵士都是80多岁的人了,还在勇攀高峰,令人敬佩。他们的证明大家别讨论了,他们的健康才是我们最关心的。”
至于哆嗒数学网的小编们的态度?当然是“谨慎的不乐观”,之前对阿蒂亚是这样,现在对李忠教授也是一样。
等到论文出世,同行评议,确定结果的时候大家再“高潮”吧,现在真还不是时候。你看,我上面写了那么多文字,前面都要加个“网传”,你们现在在朋友圈兴奋啥呢?
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文来自AskAMathematician网站。
翻译作者,ALIMJAN,哆嗒数学网翻译组成员。
校对,小米。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa


关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Jeremy Kun,伊利诺伊大学数学博士,谷歌工程师。
翻译作者,donkeycn,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文来自Reddit论坛的帖子。
翻译作者,Humphrey Liu,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa




关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
终于,在中秋节,我们一起看了阿蒂亚关于世纪大猜想黎曼猜想的证明发布演讲。这个演讲更像是一个宣称“我证明了”声明的又一次发布会,细节仍然不明朗。
不得不说,从发布会的角度来说,这是一次非常成功的“产品发布会”。人们在发布会前兴致勃勃的讨论,等待那一天的到来,直到“发布会”开始时,各路“粉丝”挤爆了海德堡获奖者论坛的官网,直播频道瞬间崩溃。论坛的工作人员不得不手举着自己的手机,来一场类似“抖音”式的山寨直播,让人心疼。
证明过程的最粗的主干,每个高中生都能理解。用的反证法,假设黎曼猜想不成立,在临界带中找一个不在临界线上的零点b,然后利用他那神奇的Todd函数T(s)构造新的一个函数F(s)。得到F(2s)=2F(s),推出F是常值零函数。从而黎曼ζ函数是零函数,矛盾。
这个思路和宣讲开始前网上就披露的PDF论文一模一样,不过有的细节不同。比如论文中引出的矛盾点是F(s)=2F(s),而不是上一段的F(2s)=2F(s),我们暂且理解成笔误。关键是那个Todd函数具体是什么,仍然不明就里——即便网上有篇据说是阿蒂亚写的关于Todd函数的论文,里面的Todd函数的定义依旧不明确——至少从数学意义上来说是不明确的,它依赖于某个物理常数。
更有网友指出,阿蒂亚的这篇论证,引用了一个他自己的错误结论。而这个错误,在他一次学术演讲中,台下的听众当场指出了。
看来,这个是否是真的有一个惊天进展,只能继续等待了。
阿蒂亚结束演讲的时候,掌声是热烈的。但在数学里,再热烈的掌声都不及专家们苛刻的审稿意见来的权威。数学里,这些专家的从来都是挑剔的,无论你之前有多少成就,论文内容就是承认你工作的唯一指标。数学里,更为残酷的是,哪怕你有500页的论文,只需要一行的错误就可以否定你的全部。
未来的时间里,人们也许会催促、等待这个证明的更多细节,甚至,讨论班、答辩会纷至沓来,直到该领域的主要专家承认或者否定这个证明。——这是最好的发展轨迹,也有可能,作者永远不公布细节、不解释,从而石沉大海。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
近日,京都大学数理解析研究所(RIMS)贴出一篇10页的简短文章《为什么abc依旧是猜想》(Why abc is still a conjecture),现在文章能在京都大学数理解析研究所(RIMS)上找到(http://www.kurims.kyoto-u.ac.jp/~motizuki/SS2018-08.pdf)阐述了望月新一教授提供的ABC猜想的论文并不能证明ABC猜想(there is no proof)。文章由两人合写,一位作者是)2018年菲尔兹奖得主彼得·舒尔茨(Peter Scholze),另外一位作者是雅各布·斯蒂克斯(Jakob Stix)也是相关领域的顶级专家。

作者在文章开篇就明确指出,文章的论证有问题,而且认为通过小修小补并不能挽救整个证明过程。 文章指出的错误是关于关键的不等式(1.5)的证明。证明中关于j²系数的取舍有不可绕过的坎。当然,出于数学家的谨慎(或者是出于礼貌),文章中两次提到是个人观点(in our opinion)。

abc猜想是一个数论猜想,最先由乔瑟夫·奥斯达利及大卫·马瑟在1985年提出。数论中,很多问题,包括一些菲尔兹奖级别的问题,都仅仅是abc猜想的简单推论。如果abc猜想能被证明,将是数论这门学科的重大进步。
2012年8月,日本京都大学数学家望月新一在其个人主页公布了有关abc猜想的“证明过程”。长达500页的证明,用到很多他自创的概念和理论。文章艰深,让众多专家也无法理解。但望月新一也没像其他学者一样,在各地举办讨论班解释他的论文,而是希望其他人自行阅读,从论文挖出更多有价值的东西——历史上格罗滕迪克的理论也有相似路径。于是,论文的正确性一直没有得到确认,一些人相信望月新一是正确的,但一些专家再没有确认之前,也表示不能认同。望月新一也撰文抱怨,数学界轻视了他的文章。于是,坊间开始流传“顶级论文无人能懂”的传说。

这回,指出其错误的舒尔茨教授,是数学界最顶级专家之一。作为顶级专家,不仅读了论文,还指出了错误。文章中也提到,望月新一试图解释他们提出的问题不是问题。结果如何,还得再看!
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
菲尔兹奖和阿贝尔奖双料得主阿蒂亚爵士(Sir Atiyah)日前声明证明了久负盛名的黎曼猜想。并将在9月24日在海德堡获奖者论坛上发表这个演讲。从目前论坛官网披露的信息来看,证明方法是一个全新的方法,但并不复杂(simple proof)。这次的证明基于之前冯诺依曼、希策布鲁赫、狄拉克的工作。
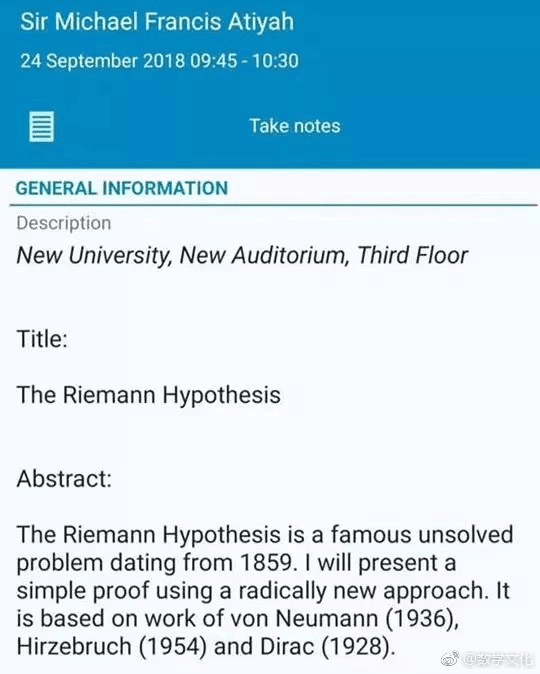
黎曼猜想是数学界最重要的猜想之一(有人说可以把“之一”两字去掉)。克雷数学研究所现在还悬赏100万美元征解。问题本身,只需要有过复变函数学习经历的人都能看懂。而它的一个等价变形,高中生都能看懂。

黎曼猜想原始版本
考虑下面一个函数项级数定义复变函数,
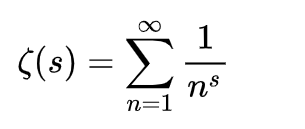
在实部Re(s)>1时,级数收敛,其余部分(s≠1)可以用解析延拓得到。解析延拓后的函数,叫做黎曼ζ函数。经过,一些简单的计算,对于负偶数,ζ(-2n)=0,那么负偶数就是黎曼ζ函数的平凡零点。而黎曼ζ函数还有别的零点,叫做非平凡零点。目前,发现的黎曼ζ函数的非平凡零点是的实部都是1/2。于是,黎曼猜想是说黎曼ζ函数的所有非平凡零点的实部都是1/2 。
高中生能看懂的版本
我们先来定义这样两个函数。
对于一个正整数n,我们把它所有的约数加起来,得到的正整数记为σ(n)。比如24的约数为1,2,3,4,6,8,12,24,那么σ(24) = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 = 60。
同样是正整数n,我们把不大于它的所有正整数的倒数加起来,记为H(n), 就是说H(n)=1 + 1/2 + 1/3 + ... + 1/n . 比如H(3)= 1 + 1/2 + 1/3 = 11/6 。
通过σ(n)和H(n),黎曼猜想等价于下面这个不等式成立:
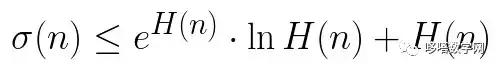
是否是“真”证明还得等待
不过,声明要得到确认,需要同行专家审稿通过。数学界内,之前也有声明证明某个大猜想,最后发现证明错误的情况。就阿蒂亚爵士本人,之前也有“劣迹”,2016年他声明证明了六维球面S6上无复结构但没有了后文。
至于这次是真是假,作为吃瓜群众只能等待了。我们哆嗒数学网小编发稿时,海德堡获奖者论坛已经崩溃。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者:John D Cook。
翻译作者,独行者,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
你将如何用公式描述一个蛋的形状呢?这里告诉你蛋的一个方程如下:
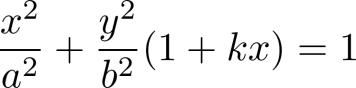
我们会发现,如果k=0,我们便会得到一个椭圆。k越大,越不对称于y轴。
我们在Mathematica上验证一遍:
代码
ContourPlot[
x^2/16 + y^2 (1 + 0.1 x)/4 == 1,
{x, -4, 4}, {y, -3, 3}
]
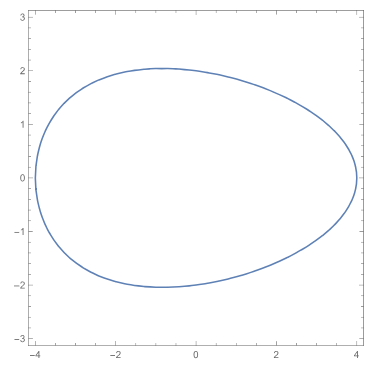
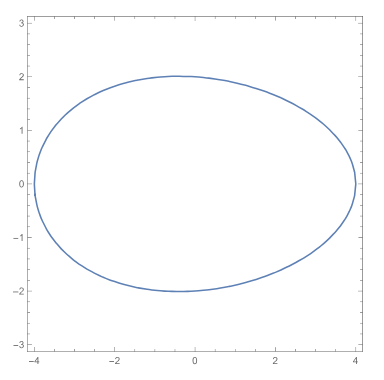
我们让k=0.05,这样看上去更像是一个椭圆。
对参数的研究
如果要对一个鸡蛋进行详尽的描述,你该如何确定a, b, k的值呢?
令y=0,则2a是鸡蛋的长度。令x=0,则2b是鸡蛋在中心的宽度。需要注意的是,这不是鸡蛋的最高位置,因为最高处在中心的左侧。(如果k是正数,则在左边。k可以为负数,这样最高处则会翻转到y轴的右边)。
我们通过确定最高处x的值来表示k。
我们有以下方程
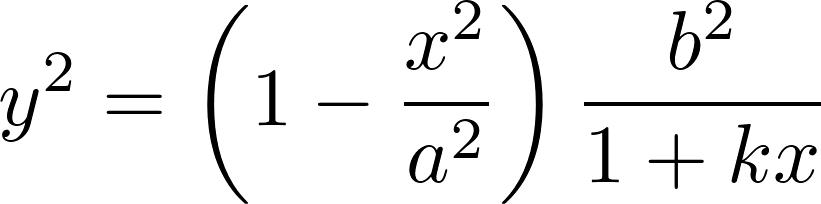
隐函数求导可知
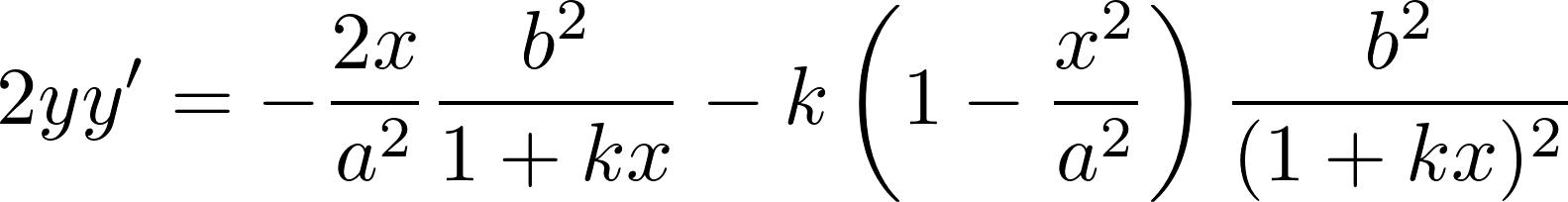
在最高处y的导数为0, 所以等式右边也应该为0。于是我们便知道了k的值。
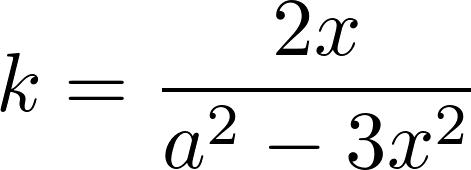
曲率
k值越大,鸡蛋便会在左边变的越平整,右边则会越尖。我们会对鸡蛋两端的变化进行量化分析。
由隐函数F(x,y)=0确定的曲线,曲率可以由以下式子算出
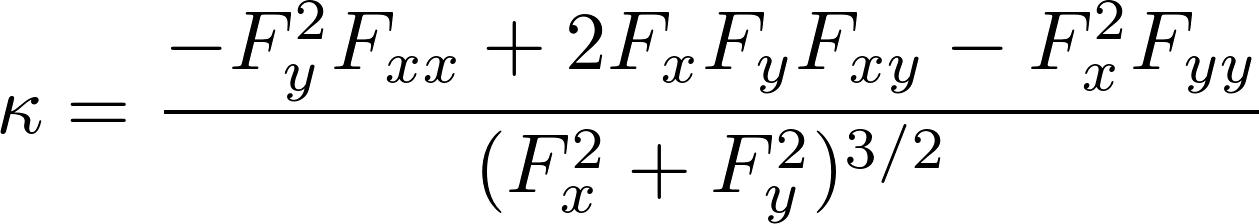
上面的等式在我们关注的(±a, 0)两个点上可以化简掉很多参数。
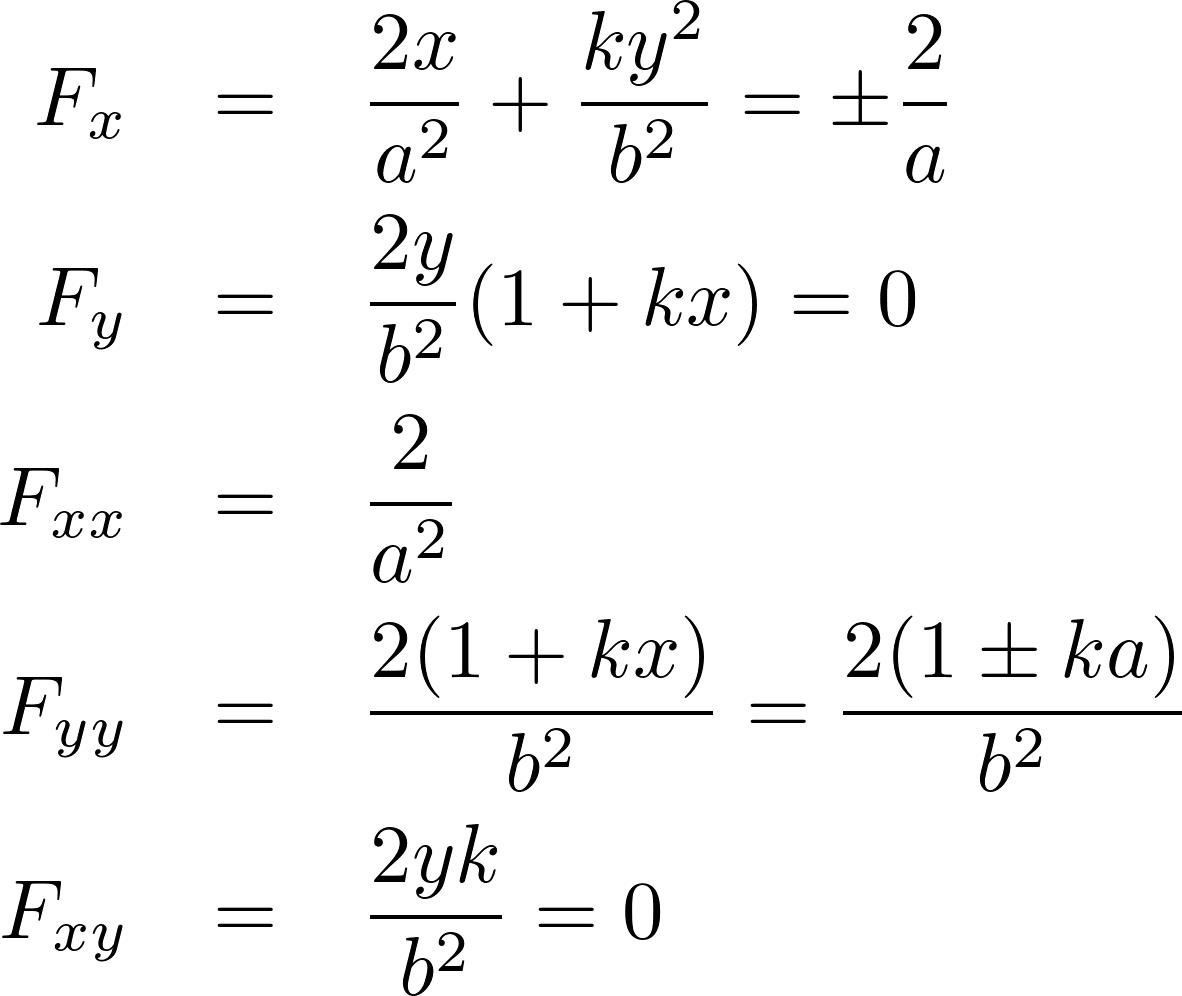
于是,曲率简化成:
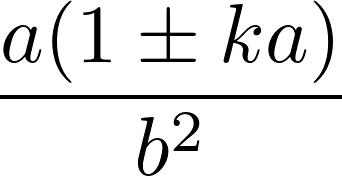
因此,在我们一开始给出的例子当中,当a=4,b=2和k=0.1时,左边的曲率为0.6,右侧的曲率为1.4。第二个例子,k=0.05,则左侧曲率为0.8,右侧曲率为1.2。
同样是这两个例子,那么如何计算鸡蛋的体积呢?

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

长久以来,“随机”的问题就令人着迷。从史前时代起,原始人就观察到了一系列不能够解释、不符合常理的现象,这些现象没有什么明显的原因,纯粹是来自大自然的“馈赠”。在最初,人们找不到什么更好的解释,于是他们归咎于神灵。日食、彩虹、地震、瘟疫、洪水或者彗星都被视为来自上天的神圣消息,只有那些能够与上天“对话”的“专业人士”才能解读。于是,这个任务往往被交给巫师、神使、祭司或者其他的萨满,这些人会在大众面前做一场全套的仪式(这就是他们谋生的手段),用来质问神灵,因为他们不再想等待让这些随机事件自己出现。换句话说,古代的人们已经开始想方设法地自己创造出“随机”效果。
“孛罗芒西”(La bélomancie),或者称之为“箭卜术”,就是非常古老的例子之一。对于想要问神的问题,将可能的各种答案写在箭身之上,然后把这些箭放在箭筒之中,摇晃箭筒并且随机抽取出一根:这就是神的回答。举例来说,公元前6世纪,古巴比伦国王尼布甲尼撒二世就是用这种方法选择他的敌人,进而发动战争。除了箭之外,人们用来抽签的物品简直多种多样:小石头、黏土片、小木棍或者彩色球。古罗马人给这些物品起了个名字叫“离者”(sors),法语中“抽签”(tirer au sort)一词的字面意思就是“抽出离者”。类似的还有“ 巫术”(sortilège)一词,这个词的原意有两个?质问神灵或者来自神灵的审判。
慢慢地,“抽签随机”的机制流传开来,在很多的应用中都能发现它们的身影。一些政治系统曾经使用过它们,比如在古代的雅典,人们用这种方法选出参加众议院五百人会议的市民,又比如,在几个世纪之后的威尼斯,人们把这种方法用在了总督任命的程序之中。“随机”同样也是游戏创作者们的重要灵感来源。人们利用它发明了猜硬币正反面游戏、带编号的色子(当然还借助了柏拉图立体的外形),甚至卡牌游戏。
正是这种能够“传递神的旨意”的随机游戏,最终吸引了一些数学家的注意力。这些数学家开始有了“玩儿转命运测量器”的奇怪想法,通过逻辑和运算,他们研究了未来将会发生的事情的概率。
所有这一切都始于17 世纪中叶巴黎科学会?博向所有与会者提出了一个他自己构思的问题。他说,试想一下,有两个玩家在玩儿随机游戏并且押了钱,先赢得3局者胜出,当玩儿到2∶1的时候,游戏被中断了,试问这两位玩家该如何分割赌桌上的赌注?
在当日与会的所有科学家中,有两个法国学者对这个问题产生了特别的兴趣,他们是皮埃尔·德·费马和布莱兹·帕斯卡。在几封书信往来之后,这两位学者最终得出的结论是,第一位玩家应该获得四分之三的赌注,第二位玩家应该获得四分之一的赌注。
为了得出这一结论,两位学者演绎了假设游戏没有被中断的、各种可能发生的场景,然后估算了玩家1和玩家2各自的获胜概率。于是,在假想的“下一轮”游戏中,玩家1有50%的概率获胜,而玩家2也有50%的概率获胜。在这种情况下,两位玩家就需要再来一轮,而这一轮当中,两位玩家的获胜概率依然是相等的,也就是说,两位玩家分别获胜的场景都有25%的概率会发生。所有关于这个游戏“未来”的可能走向,可以用下页的图表来表示。
总之,我们可以看到,在未来,玩家1有75%的概率获胜,而玩家2只有25%的概率获胜。于是,帕斯卡和费马一致认为,两者应该按照同样的比例分割赌注:玩家1拿75%,玩家2拿25%。
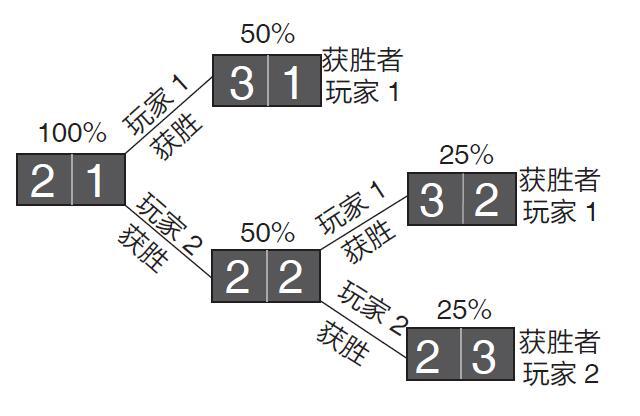
两位法国学者的推论过程可以说非常富有成效, 大部分博弈游戏( 概率游戏) 都能够用这种方法来检验。瑞士数学家雅各布· 伯努利是第一批紧跟帕斯卡和费马脚步的学者之一, 他在17 世纪尾声的时候撰写了《猜度术》(Ars Conjectandi )一书,这本书在1713 年伯努利死后出版。在这本书中,伯努利分析了经典博弈游戏,并且首度提出了概率论中的基本原则之一:大数定律。

这条定律确认了,在随机试验中,我们重复的次数越多,结果的平均值就越明显,并且趋近于一个极限值。换句话说,从长期来看,即使是最复杂的随机,最终都会产生一个平均行为,因此,所谓的“随机”也就不再存在了。
为了理解这个现象,我们倒是不必离题太远,只需要一个简单的“猜硬币正反面”游戏就能感受到大数定律的存在。假设我们投掷一枚硬币,正反面均匀,每一面都有50% 的概率朝上,可以用以下直方图来表示。

现在,假设你连续投掷硬币两次,并且记录正面和背面朝上的次数。有三种可能:两次都是反面,或者两次都是正面,或者一次正面一次反面。人们很容易认为这三种情况发生的概率是相同的,但事实却并非如此。实际上,出现一正一反的可能性为50%,而出现两次正面或者两次反面的概率都只有25%。
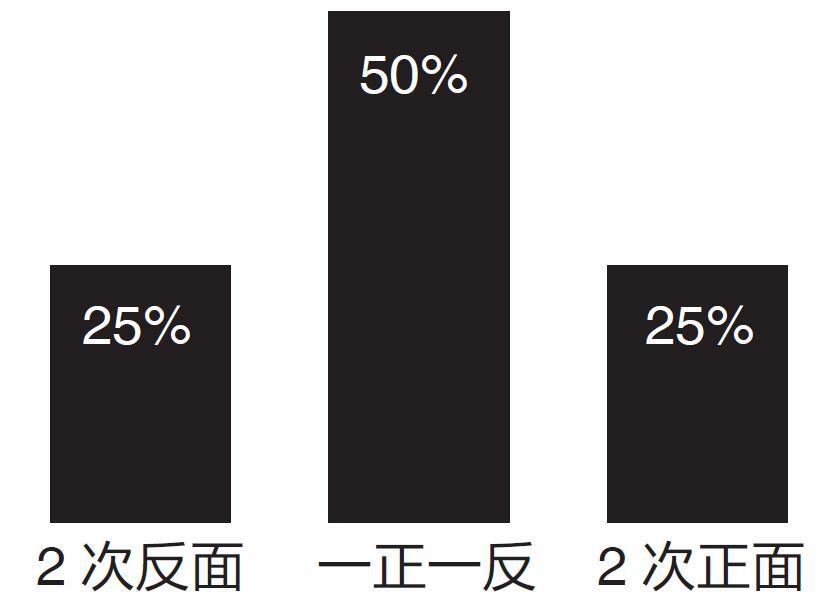
这种“不平衡”的结果,实际上是由于“两次不同的随机过程可能产生同样的最终结果”所导致的。当我们连续投掷两次硬币的时候,实际上会产生以下四种情况:反―反,反―正,正―反和正―正。反―正和正―反两种情况产生的是同一种结果,即一正一反,这就解释了为什么一正一反出现的概率是其他情况的两倍。类似地,玩家们都会知道,如果我们同时投掷两枚色子,它们的点数和等于7 的概率要远远高于等于12 的概率,因为等于7 的情况有很多种(1 + 6,2 + 5,3 + 4,4 + 3,5 + 2 和6 + 1),而等于12 的情况只有一种(6 + 6)。
我们投掷的次数越多,这个现象就越明显。最初出现机会均等的那些场景逐渐地产生区隔,一些成了极少数,一些成了普遍情况。如果你连续投掷10 次硬币, 会有大约66%的概率得到4 ~ 6 次反面;如果你连续投掷100 次硬币,有96% 的概率会得到40 ~ 60 次反面; 如果你连续投掷1000次硬币, 有99.999 999 98% 的概率会得到400 ~ 600 次反面。
如果我们分别画出投掷10 次、100 次和1000 次的直方图, 就可以看到,逐渐地,绝大多数“未来的可能”围绕着中心轴收紧,以至于那些对应着极端情况的矩形,我们的肉眼已经看不见了。
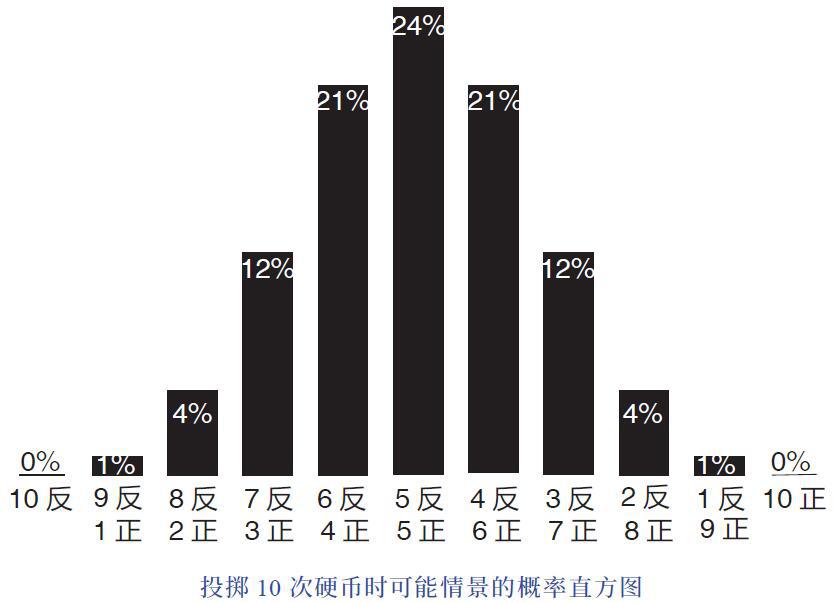
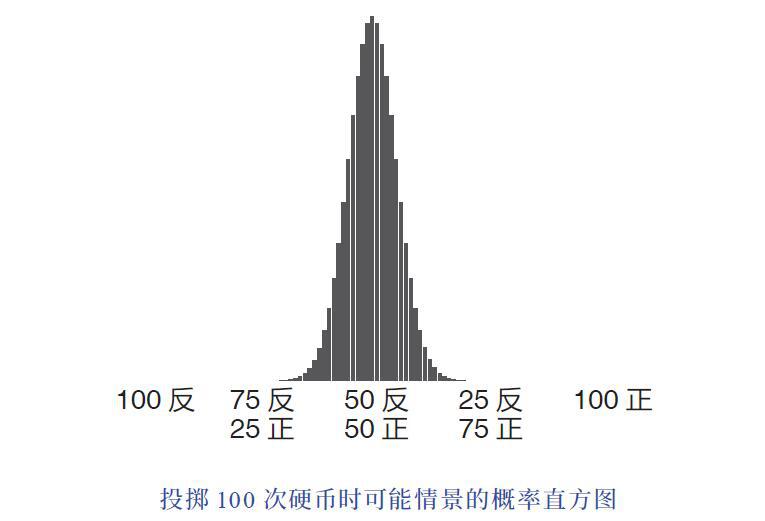
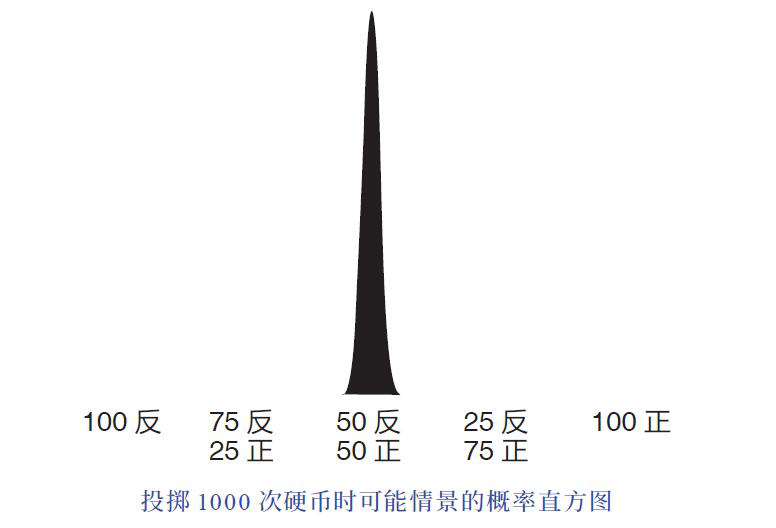
总之,正如大数定律所断言的那样:无限次地重复某个随机试验,最终的平均结果必然不再是随机的,而是无限接近一个极限值。
这一原则是测验调查和其他数据统计的操作基础。在某一人群中,选择1000 人,问他们更喜欢黑巧克力还是牛奶巧克力。如果600 人回答黑巧克力,400 人回答牛奶巧克力,则很有可能在整个群体中?哪怕这个群体总数有几百万人?比例仍然是一样的,60% 的人喜欢黑巧克力,40% 的人喜欢牛奶巧克力。调查某个随机抽取的人的口味可以被认为是一个和扔硬币猜正反面游戏相同的随机实验,只是我们的选项从正面和反面换成了黑巧克力和牛奶巧克力。
当然了,我们可能运气不好,正好抽到了1000 个人全都更喜欢黑巧克力,或者1000 个人全都更喜欢牛奶巧克力。但是这种极端情况发生的概率也是极端小的,因为大数定律向我们保证了,只要随机抽取的样本足够大,所获得的结果就有非常大的可能会接近整个人口的平均值。
进一步考察多种场景和它们在未来可能发生的概率,我们还可以建立一个置信区间,并且评估错误的风险。比如,我们可以说,有95%的可能会出现如下情况,即这个人群中喜欢黑巧克力的人数比例在57%~63%之间。实际上,任何缜密的调查研究都应该总是能获得这些可以显示其精确度和可靠性的数字。
原文作者:RHETT ALLAIN,东南路易斯安娜大学物理副教授。
翻译作者,radium,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
宛如来到一个不曾发现的海域,最妙的事情莫过于你可以通过一种新的方式找到圆周率的值,比如说,醉汉走路式的随机游走。那么问题来了,什么是随机游走?好问题!我现在就来告诉你。

你站在某个位置上开始走动。最简单的情况就是从x=0这个位置上开始。如同抛掷一枚硬币,正面?漂亮,我们向右移动一个单位。反面?也行,我们就向左移动一个单位。只要你开心,重复这个过程,那么恭喜你,你实现了一维上的随机游走。通常的,我倾向于画一个图来解释这个过程,但是今天我将用python中的随机游走代码来替代它。来看这个代码。
n=0
ball=sphere(pos=vector(0,0,0), radius=0.1, color=color.yellow)
attach_trail(ball)
start=sphere(pos=vector(0,0,0), radius=0.2, color=color.red)
while n<100:
rate(5)
temp=random()
if temp<0.5:
ball.pos.x=ball.pos.x+1
else:
ball.pos.x=ball.pos.x-1
n=n+1
ball.color=color.cyan
ball.radius=0.2
start.radius=0.2
练习代码将帮助你理解具体的过程,但我也将伪代码展现出来了。
从0到1中提取随机数
如果数字小于0.5,向x轴的正方向移动
如果数字大于0.5,向x轴的负方向移动
重复这个过程,直到你百无聊赖为止
但是随机游走一步就太没意思了,在次数较多的情况下又会发生什么情况呢?现在设置重复100步,当然,我一次性跑完,我将在-100到100之间的任何地方。但是如果我将这100步运行1000次,我就可以计算出平均情况下我会落在哪个地方。这个直方图展示了一维情况下,1000次100步的随机游走:
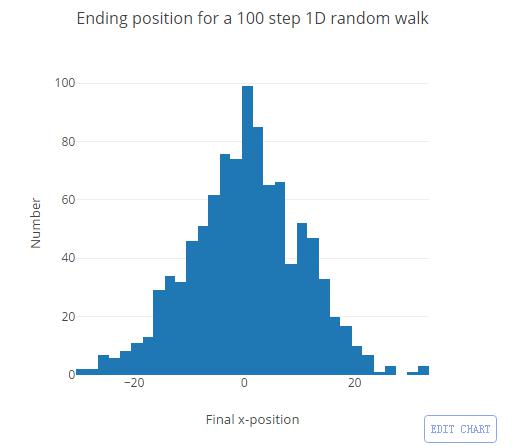
这样我就找到了一个点来描述平均位置,但为什么要这么麻烦呢?似乎很显然终点位置的平均值就在原点啊。可以理解,如果每一次我都是一相同的概率不是向左走就是向右走,很多次之后,那么我向左走的步数等于向右走的步数,好像也是,我会回到原点。
那么我们画一个从原点到终止点的总距离的图像又会怎样呢?x轴的值是取的是位移的绝对值,和从开始到结束的总距离一样。
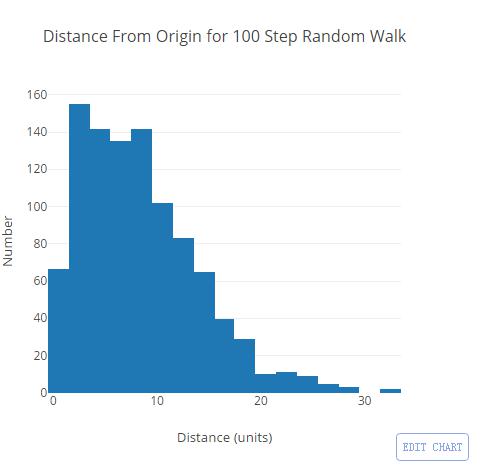
是的,事实上,这看起来很疯狂,平均的距离(不是位置)是7.848而不是0.但这也是合理的,如果你看第一个直方图,x的最终位置出现次数最多的是在x=0这个点上。但是x=-1和x=1的总次数超过了x=0上的值,而且也是取的正值,这两件事便导致了非零的平均位移。
好吧,为了不让你等太久,那我们就一起去寻找π。所以我将给你一些“派”因为我通常在π节吃派(开个玩笑,我经常在π节写π才是正道)。当然,你已经意识到随机游走的平均位移由步数所决定,恩,是这样的,但对吗?但是它将证明平均位移也由π决定。我们给出关系如下(祈求你不要叫我推导它):
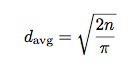
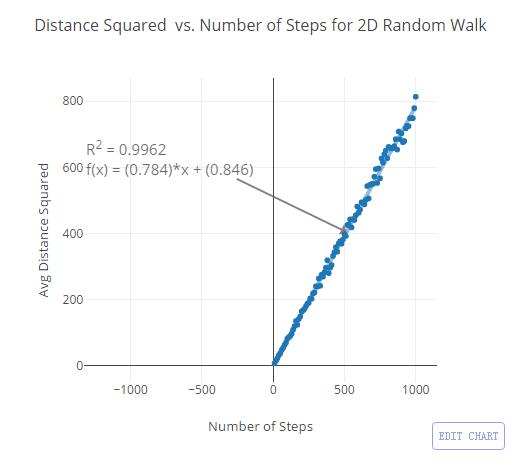
在这个表达式中,n是步数,从中,我们可以用随机游走去寻找pi的值。“A计划”如下:一次随机游走10步(做1000次,取平均值)。重复这个过程,再一次随机游走20步,30步,以及更多。如果你画一个平均位移平方关于步数的关系图,你可以得到一条斜率为2/π的直线:
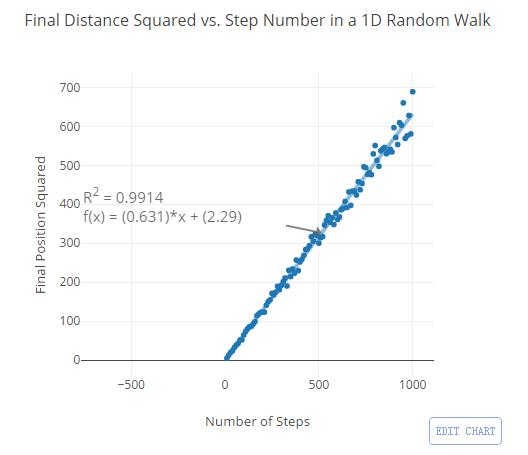
这里的斜率为0.631,因为它等于2/pi,所以我们可以得到pi值为3.1696.不太精确(π=3.1415....),但对我来说已经足够接近了。这意味着,你可以在那个区域内做一条直线去更好的估计pi。你可以通过改变每一次游走的步数去估计。当你在程序中输入更多的步数(例如1000步),嗯,我可能应该输入更多的步数,因为这样更精确。啊哦,好吧你可以去胡搞瞎搞一下。
二维的随机游走
也许这就是爱情吧,我被随机游走深深的迷住了。但总在我快要失去控制时,有人把我拉回来了。在这期间我也做了一个二维的随机游走。就像一维的随机游走一样,这时,我的每一步就有4种选择—+x, -x, +y, -y。对的,这仍然是一个离散的随机游走(一个格子状的随机游走),每一步都只有一个单位,因此我也只在坐标轴上的整数值位置。
这就是我可视化的二维随机游走100步的代码,只要你开心,你可以随意修改它。
n=0
ball=sphere(pos=vector(0,0,0), radius=0.1, color=color.yellow)
attach_trail(ball)
start=sphere(pos=vector(0,0,0), radius=0.3, color=color.red)
while n<100:
rate(25)
temp=random()
if temp<0.25:
ball.pos.x=ball.pos.x+1
elif (temp>=0.25 and temp<0.5):
ball.pos.x=ball.pos.x-1
elif (temp>=0.5 and temp<0.75):
ball.pos.y=ball.pos.y+1
else:
ball.pos.y=ball.pos.y-1
n=n+1
ball.color=color.cyan
ball.radius=0.5
start.radius=0.5
为了更“好看”,我改变了两个小球的大小和颜色,代表随机游走开始和结束的位置。看着“醉汉”在哪里乱窜,好吧,好玩吧!来,让我们来看一些有用的干货。我随机游走100步,重复1000次,平均位移会是多少呢?你期待的直方图如下:
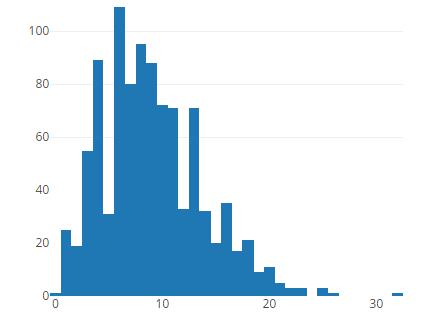
直方图告诉我们平均位移为8.820个单位。也许这不是太坏的结果,就像之前的一维随机游走一样,你可以找出平均位移和步数之间的关系:
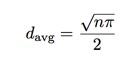
见证奇迹的时刻,我再一次绘出了平均位移的平方和步数之间在关系图,在这一个例子中,斜率为π除4.
从数据中的到的斜率,我们得到了π的值为3.136,哇哦,不太差。但这仍不是最好的方法,但很有趣哦~
让我们再随机游走一次
我保证这是最后一次随机游走了,至少在这篇帖子上是这样。这次游走仍然在二维,但有一点不同,哪有“醉汉”只在x轴或y轴方向上移动的啊?我们让每一步都成一个随机的角度进行游走。这就意味着我的走动不一定停在一个整数点上。
n=0
ball=sphere(pos=vector(0,0,0), radius=0.1, color=color.yellow)
attach_trail(ball)
start=sphere(pos=vector(0,0,0), radius=0.3, color=color.red)
while n<100:
rate(25)
temp=random()
theta=temp*2*pi
dr=vector(cos(theta), sin(theta),0)
ball.pos=ball.pos+dr
n=n+1
ball.color=color.cyan
ball.radius=0.5
start.radius=0.5
这对距离的寻找会出问题吗?我们依旧来看距离平方关于步数的图:
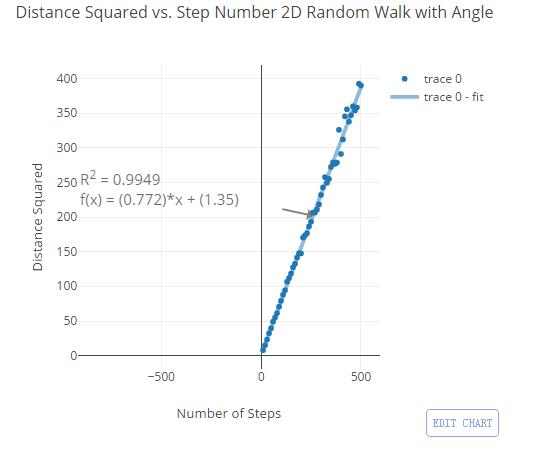
看吧,这就是我们想要的结果。这就是π,就像一位隐藏在现实世界背后的日本忍者,它会突然出现在你没料到的地方。
家庭作业
你不做点关于π的家庭作业吗?
看看是否会得到一个更好的距离平方关于步数的图。尝试多一点的步数,或许没那么多噪音。
如果你创立一个方向和每一步的大小都是随机的二维的随机游走过程,看看会发生什么?我承认这有点艰苦,因为你不能用均匀随机数(均匀分布的随机函数),除非你来决定每一步的范围。你可以限定每一步的范围从0到1,然后用高斯分布去决定每一步的大小。
尝试用三维的离散随机游走去寻找π。小技巧:你可以寻找三维中距离和步数。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者:Alucinor 。
翻译作者,风无名,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa












































关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

2018年国际数学家大会(ICM)在国际数学联盟主席森重文深思的语调中谢幕,他的发言激起了参与者对会议中最欣赏什么和学习了什么的思考.
本届大会将作为第一届在南半球举办的国际数学家大会载入史册,这是充满了激发灵感的对话、令人着迷和开天辟地的数学思想的两个星期.

来自114个国家的3018位数学家出席了这场全球数学大聚会,共计10506名与会者和416000次网上浏览. 大会的九天期间,社交网络汇集了236万人的关注.
以下是本次大会的一些高光时刻(温馨提示,视频更精彩):
悼念“闪耀之光”米尔扎哈尼

7月31日,安静而有序的人流走向报告厅参加(WM)²,史上第一届世界数学女性会议(World Meeting for Women in Mathematics,ICM2018晚上的卫星会议),见证了人们对第一位也是目前唯一一位女性菲尔兹奖得主(2014首尔ICM获得)的哀悼. 最近亡故的伊朗数学家米尔扎哈尼(Maryam Mirzakhani)为了诸如照明难题的数学方程倾其一生. 她在抽象数学方面杰出的贡献,解决了一个有关光线、台球、风和其他物体的反射与传播相关的悬而未决物理问题. 人们预言她的结论会在科学、体育和其他领域获得许多应用.
“2018菲尔兹奖得主面对面”和“为什么菲奖被誉为‘数学界诺贝尔奖’”

贝卡尔(Caucher Birkar), 费加里(Alessio Figalli),舒尔茨(Peter Scholze)和文卡特什(Akshay Venkatesh)因他们在学术领域的不同贡献,把数学界最有声望的奖项带回了家. 我们与历史学家巴拉尼(Michael J. Barany)对话,关于这惹眼的奖项,他告诉了我们一些它的历史,并消除了我们对它的一些讹传.
达斯卡拉基斯讲述深度学习与机器学习
纵贯本次数学家大会,脸书直播会采访一些具有独特个性的数学家。 “计算的诗人”、奈望林纳奖得主达斯卡拉基斯(Constantinos Daskalakis)讲述深度学习和机器学习.
贝卡尔: ”没有梦想的数学人不是数学家.“

贝卡尔以他独具创造性的数学方法和代数几何为人所知. 陈荣凯教授称他与他同事最近的工作是“双有理几何的巨大突破”. 陈荣凯叙说着贝卡尔蹒跚学步时在被战争撕裂的库尔德的生活经历,以及之后在英国寻找难民庇护的事. 陈荣凯说:“他的经历,尤其是对于那些在艰苦之地、处于困境的年轻人来说,是启发性的.”
254度灰 —— 多贝茜的美丽的逻辑财富

对于自己的工作在纯数学之外被应用,多贝茜(Ingrid Daubechies)显得很高兴. 她的突破性工作被应用于JPEG2000标准(一种电子图片的储存格式)的开发. 她独特的数学公式使得数据可以更有效地压缩和存储. 得益于她的研究,人们可以轻松地储存和发送自拍和旅拍照片了.
维拉尼举办“地球的年龄”公开讲座

在标志性的蓝色西服和绿色大领花的装束下,2010年菲尔兹奖得主维拉尼(Cédric Villani)举办了一场公开讲座,阐释了科学家们如何确定地球的真实年龄.
原文来自2018年国际数学家大会官网。
翻译作者,whymath,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
斯坦福大学的大卫·多诺霍(David Donoho)教授被授予2018年度高斯奖,以表彰其在数学领域之外获得了重要应用的杰出数学贡献。该消息由国际数学联盟(IMU)主席森重文在2018年8月1日国际数学家大会(ICM) 开幕式的上午宣布。

当日上午,里约热内卢里约会议中心内的国际数学家大会现场,官方称赞大卫·多诺霍“对数学做出的奠基性贡献”。
颁奖结果宣布后,多诺霍教授谈起了他的早年研究理论被应用到生活中时所他所体验到的乐趣。“几十年前我做了些事,当我看见它们的的确确发生在我们身边时,我感到无比的自豪。我们在改变世界这件事上拥有一种力量,这种力量让我对我所选择的事业十分满足”。
他说,所谓的数学事业并不仅限于纯数学或发表论文。“数学和世界的其它部分有极多的联系,随着时间过去,我们看到越来越多的这种联系。现代世界就是建立在数学之上的”。他随即举了智能手机的例子,其交织了大量的诸如素数分解的数学基础知识。
多诺霍教授于1957年出生在美国加利福尼亚州,他将自己的职业生涯奉献给了统计学,信息理论和应用数学的研究,并为理论和计算统计学以及信号处理和谐波分析做出了奠基性贡献。他的一些算法为理解最大熵原理,鲁棒过程的结构和稀疏数据描述做出了重要贡献。
大卫·多诺霍现任教于斯坦福大学,此前则执教于伯克利大学。他拥有普林斯顿大学的优等学位和哈佛大学的统计学博士学位。他曾在多个行业工作,包括石油勘探,信息技术和计量金融。 他曾获得麦克阿瑟奖学金(1991年),考普斯总统奖(1994年),维纳奖(2010年)和邵逸夫数学奖(2013年)。
高斯奖(Gauss Prize),是由国际数学联盟和德国数学协会联合颁发的纪念德国数学家卡尔·弗里德里希·高斯(1777-1855)的奖项,从2006年开始,在每一届国际数学家大会上颁布奖项。高斯教授在数论,统计学,数学分析,微分几何,地球物理学,天文学和光学学领域都做出了重大贡献。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文来自2018年国际数学家大会官网。
翻译作者,radium,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
在里约热内卢举办的2018年度国际数学家大会(ICM)的这个特殊仪式上,数百名朝气蓬勃的巴西中小学生收到了巴西奥数比赛的金牌---而18岁的卢卡·艾斯柯贝利就是其中的一员。卢卡来自南部里奥格兰德州立大学,他因杰出的数学能力,在富有革新精神的巴西公校奥林匹克数学竞赛(OBMEP,Brazilian Maths Olympiad for Public Schools——编者注,虽然名称是公校,其实私校现在亦可参赛了)中获得了六次金牌。而 OBMEP是世界上规模最大的中小学数学竞赛,会有超过8%巴西人口的学生参加此项竞赛考试,以测试数学水平。

去年,超过1800万青少年参加了初赛(超过智利人口!),这项竞赛由巴西基础数学和应用数学研究所(IMPA)和巴西数学会主办,覆盖了巴西全国99.6%的城市。
OBMEP协调员兼IMPA副主任克劳迪奥·拉得利姆解释说,每年都有6,500名奖牌获得者受邀请学习当地大学的课程,并从CNPq(Brazilian National Council for Scientific and Technological Development巴西国家科学技术发展委员会)获得每月100雷亚尔(约185人民币)的科学启动奖学金(PIC)。 “由大学的教授授课,教授他们在原本所在学校不能学到的学科以及讲解原本所在学校不能遇到的题目。 与此同时,我们试图激励他们继续在大学深造,“他说。
卢卡学习PIC的课程已经有好几年了,他说这些学习有助于他在目前就读的私立学校获得奖学金,并且希望在ITA航空学院学习计算机工程。 他感慨道,“因为学校里经常会有很多学生对数学不感兴趣,老师们不得不花很多时间督促他们。”PIC帮助他与一群志同道合的学生在一个课堂上,因此课程“感觉更好”(flow better——说唱音乐术语,喜欢rap的自然懂在说什么),他说。
PIC教学方法与传统的中小学课程不同,来自圣埃斯皮里图州的法比奥拉·洛特里奥(18岁)解释说,今年她和她的三胞胎姐妹一起获得了她的第三枚金牌。这三人现在在圣埃斯皮里图州联邦大学一起学习数学。 在她早期的PIC时代,法比奥拉发现很难适应不同的数学学习方式,“但是一旦习惯了它,我开始越来越喜欢数学。 之前在学校,总是专注于公式,而忽略了概念的理解。

巴西公校奥林匹克数学竞赛(OBMEP)于2005年开始举办,旨在发掘具有在数学上有一定能力的学生,目的是帮助这些青少年(从小学六年级到高中一年级) 激发他们在数学方面的潜力,重点是逻辑运用能力和创造能力,而不是传统的公式记忆。
自2005年开始举办以来,OBMEP已经对巴西所有公立中小学校的学生进行了测试,去年对私立中小学校也进行了测试。 今年13%的金牌奖给了私立教育机构的青少年。 (编者注:巴西人阿维拉(Avila)在2014年获得了数学最高荣誉菲尔兹奖)
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文来自2018年国际数学家大会官网。
翻译作者,萧瑟向来,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
康斯坦蒂诺斯·达斯卡拉基斯,现年37岁,是麻省理工学院的教授,也是2018年度奈望林纳奖的获得者。他在2018年于里约热内卢举办的国际数学家大会开幕式上被授予该奖项。

达斯卡拉基斯当前的工作专注于博弈论和机制设计。他研究出了用以理解人类博弈中策略性行为的算法和数学工具。
数学家康斯坦丁诺斯·达斯卡拉基斯的工作是他对希腊传统的终身致敬。
“希腊文学学(编者注:philology,文学学,不是文学)核心是人,” 达斯卡拉基斯说: “我的研究使用数学计算来研究人。 所以它的灵感来自于希腊观照人的传统。”
奈望林纳奖于1981年创办,用芬兰数学家罗尔夫·奈望林纳(1895-1980)的名字命名,他著有两部书,50篇文章,将数学概念介绍给非数学工作者。该奖项是理论计算机科学界最高荣誉之一。

“我喜欢质疑而不是把事情看作理所当然,” 达斯卡拉基斯在视频资料中说: “有时提出正确的问题已经向做出发现前进了一半。”
达斯卡拉基斯于1981年生于希腊雅典,以解决“纳什均衡”闻名。纳什均衡是全世界数学家已经花费六十多年试图解决的一个方程。在他关于纳什定理的博士论文中,达斯卡拉基斯追踪了阻碍纳什均衡适用性的计算障碍,并证明了需要新的,更现实的平衡概念。
“博弈论设定于已存在的、由其他人设计的复杂战略环境,而机制设计则考虑反方向的问题,即如何设计系统,以便人们彼此进行战略性交互。”
在其业余时间,达斯卡拉基斯探索希腊民俗文化。
“对希腊文化的了解越多,我的改变就越多,对希腊民族认同感就越多,”达斯卡拉基斯说。
有资格获得奈望林纳奖的数学家必须在获奖当年的1月1日不满40岁。
奈望林纳奖委员会由陳繁昌(Tony F. Chan, 中国)主持,由马尼德拉·阿格雷瓦尔(Manindra Agrawal , 印度),埃马纽埃尔·坎兹(Emmanuel Candès, 美国),沙菲·戈德瓦塞尔(Shafi Goldwasser, 以色列),尼克·欣汉姆(Nick Hingham, 英国)和乔恩·克莱因伯格( Jon Kleinberg, 美国)组成。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文来自2018年国际数学家大会官网。
翻译作者,Aria,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
京都大学的名誉教授柏原正树(Masaki Kashiwara)在2018国际数学家大会(ICM)上获得了陈省身奖. 大会开幕式早晨,国际数学联盟(IMU)主席森重文(Shigefumi Mori)颁布了这一奖项,森重文称赞了他"将近五十年工作生涯在代数分析和表示论做出的杰出和重要的工作".

柏原正树在其广泛的工作中解决了许多复杂的问题,例如Kazhdan-Lusztig猜想和量子群的晶体基理论. 在此之前他杰出的工作获得了弥永奖(1981), 朝日奖(1988),日本学士院奖(1988), 和京都数学奖(2018).
出生于1947年日本结城,柏原正树在东京大学完成了数学学士和硕士学位,并于1974年在代数分析创始人佐藤幹夫(Mikio Sato)的指导下在东京大学完成博士学位.
这位日本数学家从1984年起成为了京都大学数理所(RIMS)的高级研究员,1973成为RIMS副教授(1971年始为助理研究员). 1984年他也在名古屋大学获得副教授职位.
2010年,国际数学家大会(ICM)开始颁发陈省身奖,用于嘉奖在数学领域取得卓越成就的学者. 该奖项创立于2009年,由国际数学家联盟(IMU)和陈省身奖基金(纪念中国数学家陈省身,他毕生致力于数学研究和数学教育)合作创建. 除了24K金质奖章外,获奖者获得的50万美金将对半分给获奖者本人和他指名的机构,用于支持数学研究、教育和相关项目.
2018年陈省身奖的归属由如下成员组成的组委会裁定:主席Caroline Series (英国), Jordan Ellenberg (美国), Gerhard Huisken (德国), Michio Jimbo (日本), 和Benoit Perthame (法国).
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

哆嗒数学网成员 ALIMJAN、小米、小饕、radium 各自翻译了本文的一部分
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

贝卡尔:我飞了起来!

菲尔兹奖得主高雪·贝卡尔(Caucher Birkar)具有库尔德和英国的双重公民身份,而且还具有难民状态。“我非常高兴,同时非常兴奋。获得这个奖意味着我能继续数学研究和从事我钟爱的事业。”在2018年国际数学大会开幕式上获得菲尔兹这一权威奖项的贝尔卡满带笑容的说道。
1978年,贝尔卡出生在两伊之交库尔德地区的马里万省。现在他已经是剑桥大学的研究员了。几百年前,在这同样一片土地上,生活着伟大的数学先贤——比如,莪默·伽亚谟(1048——1131)、艾德丁·图西(1048——1131)。现在贝尔卡也追随他们来到了数学世界。“当一名库尔德人是艰辛的,”贝卡尔说到,“我们库尔德人有句俗话:‘除了大山,库尔德人没有朋友。’我希望我获奖的消息能带给4000万库尔德人哪怕一丝丝笑容。”贝卡尔生长在伊朗农村,他的哥哥在那时教了他数学。“我的父母都是农民,我应该是不可能在数学上有什么成绩的。”贝尔卡在官方的获奖视频中感谢了库尔德的传统文化,他说靠它才活了下来。
从德黑兰大学毕业后,他一直致力于解决现代数学中如极小模型,法诺簇和奇点问题等关键问题。过去8年里,贝卡尔已经为该领域做出了杰出贡献,并且已经获得了巴黎基础科学数学奖和美国数学协会摩尔奖。
对于这位年轻的数学家来说,他的职业有两个阶段。第一步是学习前人已经积累的知识。 “阅读优美的数学世界就像漫游在一个美丽的古镇。当你四处遨游时,你会发现那些华丽的建筑。第二阶段,就像突然间我有一双翅膀,我飞了起来,在城市上空鸟瞰我在地上看不到的景色。“
费加里:家庭生活还没有“最优”的最优传输专家

阿雷西奥·费加里(Alessio Figalli,)1984年出生于意大利的那不勒斯。他在最优传输理论中的贡献帮助他夺得了数学界的最高荣誉并名留数学史。
关于数学,他最喜爱的事情之一就是能够在世界上任何地方开展工作,但他的家庭生活却不像他的研究方向,远远没有达到“最优”。令人沮丧的是,他和老婆十天才能见一次面;不过他希望能很快解决这个问题。“在我的数学生涯中我已经解决了一些困难的问题,我也知道自己今后三四十年的研究方向。只有一个问题我真心希望能马上解决,那就是我能和我的老婆生活在同一个城市。”
阿雷西奥·费加里现在是苏黎士联邦理工的教授。他的工作建立了等周问题与最优传输问题之间的联系:前者在罗马神话中已有踪迹,而后者则探究运输给定质量的最优解。“他显然已经是当今全球数学界一股推动力,”路易斯·卡法莱利在一次介绍费加里工作的讲座上说道,“他的解决问题方法灵活、动态而有成效。他一定会成为这个时代最有影响力的数学家之一。”
当他还是孩子的时候,他从未意识到——或从未被告知——他对数学的兴趣将会成为一个职业。在发现了这种可能性之后,他便义无反顾地投入了这个领域并在其中展露锋芒。
文卡特什:曾经被视为神童

亚克西·文卡特什(Akshay Venkatesh),2018年菲尔兹奖得主,13岁时便开始了本科阶段的学习,并在20岁之前完成了普林斯顿大学的博士学位。“7岁左右的时候我有了这个螺旋图案的笔记本,然后开始写下这些二进制数。”他回忆道。
成为两个孩子的父亲改变了他的职业生涯和家庭生活。“在数学中,我们倾向于追求过分的完美。我觉得其实被别人强迫停止去干某件事情挺好的。孩子们就很擅长阻止你尝试去干其他事情。”他开玩笑说。
这位斯坦福教授目前在声望很高的普林斯顿高等研究院工作。这个研究院自从成立以来便“承包”着菲尔兹奖,超过半数的菲尔兹奖得主都曾在某段时间于这个研究院工作过。
作为一个在印度新德里出生,在澳大利亚长大的美国居民,文卡特什因其在数论方面的杰出贡献今天把这个数学界最有威望的奖项带回了家。他利用动力学中的想法来解决数论问题——一个上世纪70年代末密码学出现之前没有任何应用的抽象问题。
压力大的时候,文卡特什通过跑步来清理头脑和放松。如果跑的过程中还是可以思考的话,他解释道,那么他会跑得更快一些。“在你做数学的很多时候,你会卡壳。但你会觉得能够尝试去解决问题是一件很荣幸的事。你会进入一种超然的状态然后感觉自己成为了某些很有意义的东西的一份子。”他思考着说。
他的贡献在数学研究的好几个领域中都是奠基性的,他在研究中使用的探究式的富有创造性的方法也备受称赞。“多亏了他明智地创新地使用现代数学工具来研究数论,”彼得·撒纳克(Peter Sarnak)在文卡特什颁奖大会上说,“他在影响着从自守形式到表示论的很多领域。”
舒尔茨:数学中还有无穷多个问题等着我

年仅30岁的菲尔兹奖得主,彼得·舒尔茨(Peter Scholze),已经被科学界认为是世界上最有影响力的数学家之一。 然而,他是一个非常脚踏实地的人。
我经常对我想要理解的东西有一个模糊的概念,但又不知道如何用精确的语言描述它,”他说。 “直到我读了另一篇论文,突然间,我想我就可以表达了。
长长的头发以及超强看清模式之间联系的能力,他被称为“数学界中的莫扎特”。一些同时代的人不得不承认,舒尔茨的存在令他们敬畏。他是今年获得奖牌的热门人选,他获得该奖对于在该领域工作的人来说并不意外。
24岁时,他在仅5个学期完成本科课程和硕士学位后,成为德国波恩大学的正教授。
2010年,他将数论中的一个定理(哈里斯和泰勒合著的数学证明《The Geometry and Cohomology of Some Simple Shimura Varieties》)的证明从288页简化为37页,宣告了一个时代巨人的出现。
他在波恩的博导问迈克尔·拉波波特评论说,“非常荣幸能够将他从大学生时代带到最杰出的数学家之一。 他引起了算术几何学的革命,“拉波波特补充道。 “舒尔茨的作品令人瞩目的是他的创意的终极简洁性。 他定理的简洁具有深深的吸引力以及经典的荣耀。
舒尔茨获得顶级数学奖就跟玩一样: 欧洲数学学会奖(EMS),2016莱布尼兹奖(Leibniz),2015费马奖(Fermat),2015奥斯特洛斯基奖(Ostrowski),美国数学会Cole奖,2014克雷研究奖(Clay Research),2013拉马努金奖(SASTRA),Prix奖和Cours Peccot奖的前任获奖者。 现在,他用菲尔兹奖章将樱桃放在蛋糕上作为点缀。
他的工作重点是建立算术和几何之间的桥梁。 尽管已经取得如此大的成就,但他的潜力依然深不可测,而舒尔茨根本没有放缓的迹象。 “一旦你解决了一个问题,就会有10个问题随之而来,”他解释道。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
根据2018国际数学家大会(ICM)官方网站消息。2018年被视为国际数学最高奖项的菲尔兹数学奖已经揭晓他们是:
就职于剑桥大学的伊朗裔英国数学家 高雪·贝卡尔(Caucher Birkar)
For his proof of the boundedness of the Fano varieties and for contributions to the minimal model program.
表彰其证明法诺簇的有界性并对极小模型程序的贡献;

就职于苏黎世联邦理工学院的意大利数学家阿雷西奥·费加里(Alessio Figali)
表彰其最优传输理论及其在偏微分方程、度量几何和概率论方面的应用;
for his contributions to the theory of optimal transport and its applications in partial differential equations, metric geometry,and probability.

就职于波恩大学的德国数学家彼得·舒尔茨(Peter Scholze)
表彰其将p进制域上的算术代数几何转换成对拟状完备空间(perpectoid space)并将其应用在伽罗瓦表示论上,以及对上同调理论的发展做出的贡献;
For transforming arithmetic algebraic geometry over p-adic fields through his introduction of perpectoid spaceS, with application to Galoids representations and for the development of new chomology theories.

就职于普林斯顿大学印度裔澳大利亚数学家亚克西·文卡特什(Akshay Venkatesh)
表彰其综合解析数论,齐次动力系统,拓扑学和表示论的贡献;
For his synthesis of analytic number theory,homogeneous dynamics, topology,and representation theory

感谢 小饕、萧瑟向来、ALIMJAN、math001 第一时间的翻译
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信: DuoDaaMath 每天获得更多数学趣文
新浪微博: http://weibo.com/duodaa
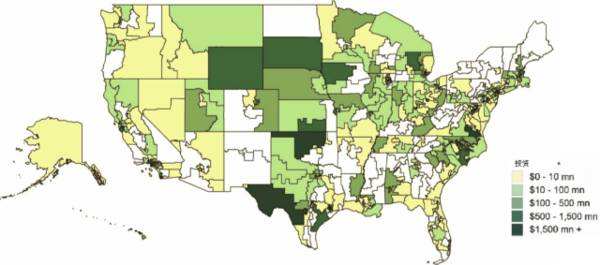
2018年世界大学学术排名,也就是俗称的上海交大版大学排名,日前公布一流学科排名,我们哆嗒数学网依然只是关注数学学科的排名。

数学学科排名方面,美国院一如既往的表现出色,占据前十名中的六个席位。而英国和法国分别占据两席。第一到第十分别是:普林斯顿大学(美国)、巴黎第十一大学(法国)、斯坦福大学(美国)、牛津大学(英国)、纽约大学(美国)、麻省理工学院(美国)、剑桥大学(英国)、加州大学洛杉矶分校(美国)、索邦大学(法国)、加州大学伯克利分校(美国)。
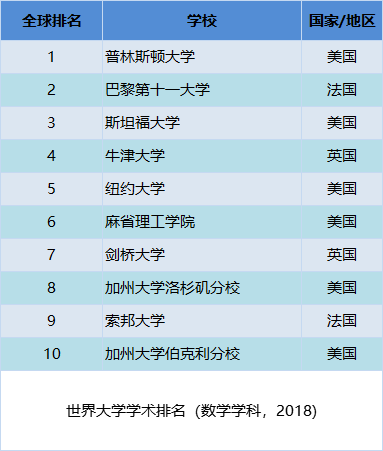
值得一提是数学榜单前十中的新面孔法国索邦大学。这个学校与2018年1月由巴黎第六大学(又名皮埃尔和玛丽居里大学)和巴黎第四大(又名巴黎索邦大学)学合并后组成。而索邦正好是之前四大的名称。合并之前,六大以理工科为主、四大以文科为主。2010年,法国政府启动“卓越大学计划 ”,希望通过重组实现学术资源的深层整合,从而吸引最优秀的教师、研究人员和学生进入法国顶尖大学,最终提高法国高校在国际上的学术知名度,同时提升法国科学成就的世界影响力。在此背景下两所强校合并,并沿用在欧洲有着悠久历史传统,被誉为"欧洲大学之母"的欧洲中世纪的索邦神学院的名称。——这是一个例子,说明类似中国“双一流”高校建设的政府计划,一些西方国家同样在实施。
亚洲方面,日本的京都大学排名第一,总排名17名。以色列的耶路撒冷希伯来大学排名第二,总排名第19。沙特阿拉伯的阿卜杜勒阿齐兹国王大学排名第三,总排名第29。来自中国的北京大学排名第四,总排名第40。下面的亚洲前十因为并列原因,其实有15所高校。
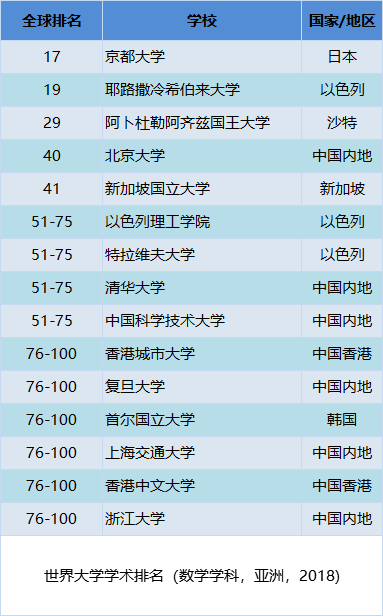
中国高校有74所大学进入榜单。在中国的高校的排名中,排名第一的是北京大学,世界排名第40名。是唯一一个进入前50名的中国高校。哆嗒数学网下面再为你奉上所有中国高校的排名。

关注微信:DuoDaaMath 每天获得更多数学趣文

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
足球世界杯刚结束,四年一度有着“数学界奥运会”之称的国际数学家大会即将在8月在巴西里约热内卢开幕。届时,大会将颁发数学界最高荣誉的菲尔兹奖。
谁将获得菲尔兹奖呢,国外有个投票网站做了一次投票,结果非常有趣。其实,在菲尔兹奖的评选上,也经常会有“大热必死”现象。因为获奖有40岁的年龄限制,所以有传言,评委会优先考虑最后一次机会获奖的人。另外,很少情况下,会将奖颁发给同一个国家或者同一个学校的人。所以下面的舒尔茨和布伦德也许在国籍上会有冲突。
我们将前10名和大家一起讨论。
第十名 胡戈·度米尼尔-柯平(Hugo Duminil-Copin) 法国

概率论、随机过程专家,现为日内瓦大学教授。
度米尼尔-柯平对伊辛模型的研究情有独钟,此模型在物理研究中有着特别的地位。度米尼尔-柯平对此模型的研究让他收获无数荣誉。
所获奖项:2013奥博沃尔法赫奖、2016欧洲数学会奖、2017科学突破新视野数学奖、2017雅克·埃尔布朗奖、2017勒夫奖
第九名 詹森·米勒(Jason Miller) 美国

概率论、随机过程专家,现为剑桥大学教授。
他与Sheffield一起关于高斯自由场的研究(GFF),奠定了他在随机游走、布朗运动研究方向上的学术地位。
所获奖项:2015戴维逊奖、2016怀德海奖、2017克雷研究奖
第八名 张伟(Wei Zhang) 中国

数论专家,现为麻省理工教授。
很高兴在这个列表中看到中国人。他在博士二年级的时候,他对库达拉(Kudla Conjecture)猜想的工作,让他在数论领域崭露头角。张伟的成名作是和恽之玮合作,对L函数为L函数的泰勒展开的高阶项提供几何解释。
所获奖项:2013拉马努金奖(SASTRA)、2016晨兴数学奖、2018科学突破新视野数学奖
第七名 西蒙·布伦德(Simon Brendle) 德国

微分几何、偏微分方程专家,现为哥伦比亚大学教授。
布伦德解决了共形几何中关于山辺英彦方程(Yamabe Equation)相关的一些主要问题。另外,他和Schoen合作证明了微分球面定理(differentiable sphere theorem),这是整体微分几何的基础问题。他还证明了向武义-劳森猜想(Hsiang–Lawson's conjecture)。
所获奖项:2012欧洲数学学会奖、2014博谢奖、2017费马奖
第六名 马丽娜·维娅佐夫斯卡(Maryna Viazovska) 乌克兰

离散几何专家,现为国立基辅大学教授。
维娅佐夫斯卡大学时期,获得了2次国际大学数学竞赛(IMC)的第一。维娅佐夫斯卡的成名作是解决了8维空间的球体堆积问题,她还和同事一起解决了24维的球体堆积问题。在此之前,人类只是解决了3维和3维以下的球体堆积问题。而3维情况的解决使用了大量的计算机计算,而维娅佐夫斯卡的8维和24维情况的证明,却被人形容为“简单的让人吃惊”。
所获奖项:2016年塞勒姆奖、2017克雷研究奖、2017拉马努金奖(SASTRA)、2017欧洲组合学奖、2018科学突破新视野数学奖
学生时代奖项:国际大学生数学竞赛两次第一
第五名 乔迪·威廉姆森(Geordie Williamson) 澳大利亚

群论几何表示论专家,现为悉尼大学教授。
威廉姆森是澳大利亚科学院史上最年轻的院士。威廉姆森对Kazhdan-Lusztig猜想用纯代数方法重写和简化了证明。在这个过程中,威廉姆森研究出了一种技术手段,在群论的诸多问题中,使用这个技术手段可以得到一些的重要成果。
所获奖项:2016年接连获得谢瓦莱奖、2016欧洲数学学会奖、2016克雷研究奖、2016科学突破新视野数学奖
第四名 齐普里安·马诺列斯库(Ciprian Manolescu) 罗马尼亚-美国

规范场论、低维拓扑专家,现为加州大学洛杉矶分校教授。
马诺列斯库在学生时代是数学竞赛的高手,连续三届以满分获得国际数学奥林匹克竞赛((IMO))金牌。进入学术生涯后专注于低维拓扑的研究。2013年在马诺列斯库发表了一篇论文,否定的解决了5维以及5维以上的流型中的三角形解剖猜想。
所获奖项:2012欧洲数学学会奖、2017费尔特里内利奖
学生时代奖项:国际数学奥林匹克3金、摩根奖
第三名 阿雷西奥·费加里(Alessio Figalli) 意大利

变分法、及偏微分方程专家,现为苏黎世联邦理工学院教授。
费加里在做运输优化理论的相关问题时,问题和蒙日-安培方程联系了起来,他和Philippis一起工作,得到了关于这个方程的一些重要结果。他擅长于一个技术手段,把本来看似是偏微分方程的问题转化为几何不等式的问题。以至于后来很多重要的方程,他的工作有所涉及,比如哈密顿-雅克比方程、薛定谔方程、伏拉索夫-泊松方程。
所获奖项:2012欧洲数学学会奖、2017费尔特里内利奖
第二名 费尔南多·马克斯(Fernando Marques) 巴西

几何、拓扑以及偏微分方程专家,现为普林斯顿大学教授。
马克斯的的成名作是和Neves一起解决了Willmore猜想。另外,去年他和Irie, Neves一起声明解决了某种一般情况下的丘成桐猜想,并把论文挂在了网上。
所获奖项:2013拉马努金奖(ICTP)、2016维布伦几何奖
第一名 彼得·舒尔茨(Peter Scholze) 德国

算术代数几何专家,现为波恩大学教授。
学生时代的舒尔茨多次参加国际数学奥林匹克竞赛(IMO)获得三金一银。24岁时,成为德国历史上最年轻的正教授。舒尔茨在博士论文中提出了状似完备空间(perfectoid space)的概念和与之配套的相关技术手段。利用该技术手段也可将霍奇理论中的法尔廷斯近纯定理(almost purity theorem)加以推广。此技术手段还能提供新角度展现其它问题,在志村簇或由拉坡坡特(Rapoport)和钦克(Zink)引入的空间中都可找到实例。
所获奖项:2013拉马努金奖(SASTRA)、2014克雷研究奖、2015费马奖、2015奥斯特洛斯基奖、2015柯尔代数奖、2016莱布尼兹奖、2016科学突破新视野数学奖(本人谢绝)、2016欧洲数学学会奖
学生时代奖项:国际数学奥林匹克3金1银
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
2018国际奥林匹克数学竞赛(IMO)刚刚公布。中国队连续四届与团体第一无缘,以199的总分获得第三名。第一名是美国,212分,第二名是俄罗斯,201分
此次比赛,团体第一的归属由关键是第6题决定。而这一题中国获得19分(满分42分),美国获得31分,俄罗斯获得23分。
另外,中国台湾179分,排名第6,中国香港,89分,排名第49。中国澳门61分,排名第65。
中国队从上世纪八十年代开始就是国际奥林匹克数学竞赛的霸主,他们1989年到2014年期间25次参赛,获得19次团体第一。而从2015年开始,因为美国、韩国等国家也开始效仿中国的数学竞赛集训模式,实力增强,在最近的四届竞赛中,美国获得三次第一,另外一次被韩国获得。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Dr. Dilts,俄勒冈大学数学博士。
翻译作者,风无名,哆嗒数学网翻译组成员。
校对,Math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
哥德尔的不完备定理是那种能把你脑浆敲出来的一个定理。

在上一篇博客,我们讨论了定理本身及其影响。简单说来,它们显示出了数学本身的内在局限性。
哥德尔第一定理与一致性、可证明性这两个概念有关。一个数学系统(由一些假设组成,这些假设被称作是“公理”)称为一致的,如果它们没有矛盾存在。换句话说,你不能证明一个既真又假的语句。
在任何逻辑系统内,都有很多语句,也就是那些你能说出的东西。比如,我像这样说“所有的素数都比十亿小”。它是一个错误的语句,但是我仍能说出它。

但是,仅仅因为我能说出一个语句,并不意味着我可以证明它为真或者假。大多数情况下,那个语句是难以证明的,所以你不知道如何证明它。可是,还有一种可能,存在既不能证明为真,也不能证明为假的语句。这种语句,我们称为不可证明的语句。任何拥有不可证明语句的逻辑系统(公理集)成为不完备的。
哥德尔第一不完备定理说了:如果你有一个一致的数学系统(也就是,一堆互不矛盾的公理),并且你可以做算数运算,那么,一定存在使用那些公理不能证明的语句。[原注1]
换句话说,数学是不完备的。证明所有的事情,是不可能的。(译者注: 笼统地说数学是不完备的,是不对的。此文作者这里提供的是一个不严谨的简单说法。)
哥德尔第一不完备定理的最基础的想法,就是这句话:“这句话是不可证明的”。
如果你能证明这句话是正确的,根据定义,它就是可证明的。但是这句话自己说了它是不可以证明的;同时由于它是真的,它也是不可以证明的。但是它不能既是可证明的又是不可证明的。因此,这句话必须只能是不可证明的。
虽然这就是我们将来采用的基础的想法,问题是,在数学里面,并不存在一个明显的形式化的方法来说“这句话是不可证明的”。你说的可证明是什么意思?“这句话”指什么?使用什么公理呢?
哥德尔的证明必须让所有的这些都完美的严格化。
第一步要证明的是:任何严格的数学语句都可以转化为一个数,反过来也可以。

这一步是精妙的,不过并不复杂。从某种意义上说,这就像一段代码,它把每一字母都转化成一个数。比如,我们可以这样做:a转换成1,b转换成2,等等。单词”math"将会转化成"13-1-20-8"。计算机也使用了类似的模式来把文本存储像成0和1的形式。
为了把数赋给严格的数学语句,哥德尔使用了类似的方法来进行编码。实现这种编码的方式并不唯一,不过我将要讲一种与哥德尔最初的方法比较接近的方法。

第一步,对于你的某个数学系统的每一个数学符号,给予一个数。[原注2]比如,也许”0"被存储为1, “=”被存为储2, "+"存储为3.
一条数学语句就是这些符号的一个列表。使用数对单个的符号进行编码,就可以等价地说,语句就是数的列表。例如 0=0等价于(1,2,1)。
为了把语句编码为唯一的数,我们让它的哥德尔数等于一部分素数的幂的乘积,幂的次数为数学符号在列表中的位置。因此,0=0的哥德尔数是2^1 · 3^2 · 5^1 = 90。
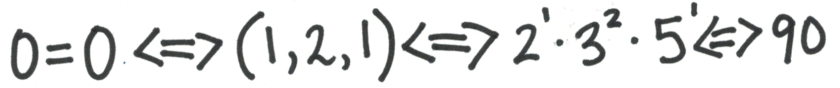
对于一个语句S,比如”0= 0”,我们使用记号G(S)来指代它的哥德尔数。因此,G(0=0) = 90。
正如你意识到的,即使是对中等长度的语句,哥德尔数也会很快变得非常大。不过,大小不是一个问题,我们不需要把它们写下来,你只需要知道这样的数存在就可以了。

关键的问题是:对于任一个数,我们可以返回来得到一条数学语句。
每一个数都可以唯一地分解为素数的乘积。如145530 = 2^1 · 3^3 · 5^1 · 7^2 · 11^1,所以145530代表了 0 + 0 = 0.
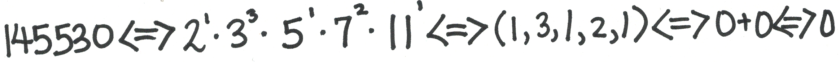
任一严格的数学语句都可以用这种方式翻译成一个数。乃至一个证明,也仅仅是一些捆绑在一起的语句而已。(“A” 蕴含“B”, 并且“B”蕴含“C”,所以“A”蕴含“C”)。那就意味着,我们展示了所有的数学都能够仅用数来写出来。[原注3]
类似地,存在一个算数的方法来检查一串使用哥德尔数来表示的语句,是否是另一串使用哥德尔数来表示的语句的证明。[原注4]
把数学语句翻译成数,看起来像是有趣的技巧,它是哥德尔不完备定理的证明的关键。
它如此重要的原因在于,它让我们把任何关于证明、可证明性的问题转化为关于数的算数问题。因此,为了证明任何(可证明的)语句,我们可以仅仅使用数以及数的性质。

例如,考虑这个被我称为Unprovavle(y)的语句。这个语句是:“y是某个语句的哥德尔数,并且不存在一个数x使得x是那个语句的证明的哥德尔数”。
因此,unprovable(y)本质上在说“y所代表的语句”是不可证明的。但是,它除了是一个关于证明与语句的问题以外,它还完全是一个关于数、数的算数关系的问题。
这个准确的算术关系是非常复杂的,不过的确可以被精确地定义。类似的,Prime(y),这个简单得多的语句语句“y是一个素数”, 存在一个算术关系Unprovable(y)。于是,Prime(y)断言了一个数如何,这个断言可以被一些相对而言比较简单的算术来判定。
现在,我们将来来带长途征程的最后一部分了。

哥德尔的证明的本源的想法是这句话:“这句话是不可证明的”。使用Unprovable(y)这句精确的数学语句,我们可以让这句不精确的语句完全精确。[原注5]
为了得到“这句话是不可证明的”的精确版本,我们将使用 “对角线引理”。(一条引理只是你用于证明其它定理的定理[原注6])。对角线引理表明了,就我们正在使用的数学系统而言,存在一个语句S它满足:S是真的,当且仅当Unprovable(G(S))是真的。(注意,unprovable(y)的输入是某个语句的哥德尔数。这个例子中,这个语句即S)
清楚一点说,对角线引理并没有证明S或者Unprovable(G(S))是真的,仅仅证明了它们或者同时为真或者同时为假。你开动脑筋,想想这到底啥意思?

对角线引理也表明了:一个未知的可能非常长的数学语句S,是真的,当且仅当 unprovable(G(S))是真的。但是unprovable(G(S))是真的,(根据unprovable(y)的定义)意味着S是不可证明的。
所以,如果我们能够证明“ 语句S是真的”,对角线引理表明我也能证明“unprovable(G(S))是真的”。但是,unprobable(G(S))说的是“S是不可证明的”!因此,S既是可证明的又是不可证明的,这就是一个矛盾。
因此,S必然是不可证明的。
语句S就是我们正在寻找的 “这句话是不可证明的” 这个语句的准确的版本。因此,不是每一个语句都是可以证明的。
可怜的数学,被人玩坏的数学……

[原注1] 关于数学系统,还有很多更加技术性的假定,比如,它必须是“有效的”,又叫做“可递归地枚举的”。对哥德尔的证明来说,这些假定是至关重要的。就我想向外行读者做介绍的这篇文章的主要部分来说,我觉得它们过于技术化了。我会在后面的脚注里面解释为什么那个系统需要是有效的。
[原注2] 算术的公理化也就是皮亚诺算术。皮亚诺并没有直白地提及所有的自然数。事实上,它仅提及了0.它拥有一个能否计算下一个数的“后继函数”S。因此,S(0)就是1的定义,S(S(0))是2的定义。所以,当把数学语句翻译成哥德尔数的时候,我们的编码仅需要给0、S赋值,而不需要给每一个数单独赋值。那意味着我们的编码仅需要考虑有限多个符号。
[原注3]这里指任何从我们的公理、选定的符号所生起的数学。
[原注4] 在上一篇文章中,我们忽略了很多重要的技术性的假设。其中之一,在这里说一下。那就是,你的数学系统(公理的集合)是有效的(effective)。在本质上,这意味着,存在一个这样的计算机程序:从理论上,能够列出你的数学系统的所有定理,而不列出任何不是定理的语句。对于不完备定理所考察的基本的数学系统——皮亚诺算术, 这一点是真的。对于标准集合论(ZFC),这一点也是真的。还存在一些不有效的系统,它们趋向于无用或无趣。比如有一个这样的系统:把算术中所有真的语句都作为公理。于是,任何真的东西都是公理,从而证明上是平凡的。为了让算术证明的校验(check)能工作,你的数学系统是有效的,这个假定是至关重要的。
[原注5] 哥德尔找到了一个直接说这个语句的方法。我们会采取一个略微不同的、更容易理解的途径, 不过哥德尔证明的主要动机是一样的。
[原注6] 引理一般是相对容易证明的,对角线引理也是这样。然后,它的证明是技术性的,并不是很有启发性。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
混迹娱乐圈和体育圈的人很多时候给大家的感觉是,前者头脑简单,后者四肢发达。而数学专业内的人给多数人的感觉是有着极高智商的“书呆子”。我相信,很少有人两者联系起来。而下面我们盘点的10位娱乐圈和体育圈的明星,他们曾红极一时,却是(或者曾经是)数学专业的。
第十名 约翰·尤索
如果你喜欢看美国橄榄球联盟NFL的球迷,你一定多少听过约翰·尤索这位球员。他曾经是巴尔的摩乌鸦的护锋。限于美式橄榄球运动在中国的爱好者并不多,所以尤索在中国并不出名。但是在美国的推特上,尤索可是红极一时的“网红”,出名的原因是他球员和数学家的双重身份——一位五大三粗的橄榄球球员做数学研究,这画面……好美!
尤索在球员时期还在撰写数学论文,并发表在专业杂志上。他还在训练比赛之余,去各个大学开数学讲座,分享数学成果。现在他从球员生涯退役了,去了麻省理工继续攻读数学博士,极有可能走向数学学术的道路。
第九名 格伦·约翰逊
如果你是英超的球迷,一定会对格伦·约翰逊影响深刻。约翰逊司职右后卫,在2009年到2012年,是这位球员的巅峰时期。在这段时间内,这位黑人球员站稳了利物浦和英格兰国家队主力位置。2010年,代表英格兰参加世界杯,止步16强。而16强英德大战中约翰逊就在场上。那场比赛兰帕德明显越过门线的吊射被判无效,加速催生后来足球运动的门线裁判、门线技术以及视频VAR裁判技术。

令人意外的事情是,格伦·约翰逊在他职业生涯的巅峰时期还利用业余时间在开放大学攻读数学学位。其实欧洲很多球员在很多时候都在同时考虑退役之后的事情,不少人也会去修个学位。小编觉得约翰逊修数学学位并不是想成为数学家,而是通过一种训练提升对数字的敏感,这对退役后的财务运作有所帮助。
第八名 奥特马尔·希斯菲尔德
如果你是德甲的老球迷,对这个名字绝对不会陌生。这个名字会让你想起巴斯勒、埃芬博格、卡恩的时代。希斯菲尔德在德甲是绝对功勋教练,长期职教过多特蒙德、拜仁慕尼黑两支球队。作为球队主教练,他总共获得过7次德甲冠军、2次欧冠冠军。

当他在瑞士巴塞尔踢球时,他用业余时间在附近的略拉赫学园(Lorrach College)修得了数学教师和体育教师的执照。而希斯菲尔德本人也提到过,数学的思维方式对他排兵布阵有所帮助。
第七名 泰瑞·海切尔
如果你喜欢看美剧,一定会知道这部曾经大红大紫的电视剧《绝望主妇》。而剧中让人又爱又恨的女主之一的苏珊的扮演者正是泰瑞·海切尔。

海切尔大学期间在加州丘珀蒂诺的德安扎学院(De Anza College)就读,专业是数学与工程。业余时间海切尔经常去旧金山的音乐戏剧学院学习表演。后来把握了一次试镜的机会,走向职业演员道路。
第六名 约翰尼·巴克兰
如果你喜欢英国的摇滚音乐,一定会知道酷玩乐队(Coldplay)。无论你是否喜欢他们,酷玩乐队在商业上获得了巨大的成功。2005年,发行的专辑《X&Y》年终销量830万张,成为国际唱片工业联合会年度全球销量冠军。2008年,发行的专辑《生命万岁》(Viva La Vida)年终销量660万张,获得格莱美奖最佳摇滚音乐专辑奖。

酷玩乐队的主吉他手是约翰尼·巴克兰,学生时代他在伦敦学院大学的专业是天文与数学。实际上酷玩乐队的很多歌曲都显示出对数学的偏爱,从曲名可见一斑:《X&Y》、《Twisted Logic》、
《Square One》,《Proof》,《Major Minus》等等。
第五名 大卫·罗宾逊
如果你是NBA的老球迷,一定知道这位拥有“海军上将”称呼的前马刺队中锋。这位1987年的状元秀在上世纪90年代和另外一位NBA的超级巨星蒂姆·邓肯组成了在全联盟叱咤风云的“双塔”,并在1999、2003年获得总冠军。而罗宾逊的个人荣誉也不少,拿过常规赛MVP、得分王,多次入选全明星阵容、最佳阵容、最佳防守阵容。

而鲜为人知的事情是,罗宾逊还是一位学霸。1983年,大卫·罗宾逊高中毕业,在SAT考试中取得了1320分(满分1600分)的优异成绩,他选择进入美国海军学院主修数学(这也是他绰号的由来)。
第四名 布莱恩·梅
喜欢摇滚的粉丝应该没人不知道皇后乐队(Queen)吧。皇后乐队是史上最成功的摇滚乐队之一,今年1月还刚刚获得第60届格莱美奖终身成就奖。就算你不知道乐队的名字、不知道他们是哪些人,但你一定听过他们的歌——《我们是冠军》(We Are The Champions)和《我们将震撼你》(We Will Rock You)。布莱恩·梅是这个乐队的吉他手。

布莱恩·梅在帝国理工学院上学的时候,攻读的是数学和物理专业。在音乐上成名后,2006年有返回学校,攻读天文学博士,并继续做天文学的学术研究。为表彰布莱恩·梅的贡献,2008年,一颗小行星还用他的名字命了名。
第三名 保罗·范霍文
《机械战警》这部电影在中国有万千粉丝,而这部经典科幻电影的导演就是保罗·范霍文。注意,这里《机械战警》说的是1987年的版本。范霍文的《机械战警》1300万美元成本,票房收入5300万美元,在30年前是绝对的神作。而范霍文1997年《星河战队》也被奉为经典。

范霍文学生时代在位于荷兰在欧洲久负盛名的莱顿大学读书,专业是数学和物理。虽然范霍文对数学并不十分感兴趣,但由于本人的天赋实在很好,也顺利的拿到了数学和物理的双博士学位。按范霍文的说法,他后来的职业生涯,他从来没用这个博士学位当过任何事务的敲门砖,而是全身心的投入到他的导演艺术创作中。
第二名 刘易斯·卡罗尔
《爱丽丝梦游仙境》又译《绿野仙踪》是畅销上百年的奇幻小说。在出版后的一百多年时间里,小说被改编成各种动画片、电视剧、电影等各种形式的艺术作品。作者刘易斯·卡罗尔其实是笔名,他的本名叫查尔斯·道奇森。

道奇森在数学上非常专业,因为他就是牛津大学的数学讲师,说是数学家也不为过。但是,数学界的道奇森与文艺界的卡罗尔相比,知名度可以忽略不计。卡罗尔不喜欢那个时代兴起的抽象代数,《爱丽丝梦游仙境》里也有对抽象代数的讽刺和调侃。其中那个著名的爱丽丝和疯帽子的茶会,据说就是对哈密顿四元数的嘲讽。百度“四元数派对”可以收到我们哆嗒数学网对此的专门介绍。
好,我们倒数三声,迎接第一名!
三!
二!
一!
第一名 迈克尔·乔丹
我相信你看这的时候一定会大吃一惊。迈克尔·乔丹被认为是史上最伟大的篮球球员。他的名字如此家喻户晓,已经超过了篮球运动本身。在这里介绍迈克尔·乔丹球员时代的成绩已经不合时宜,我相信看过、听过他战绩的人都能如数家珍地盘点出不少乔丹的“高光时刻”。乔丹无愧于“篮球之神”的称号。

你一定不知道,乔丹爱数学,甚至他曾经是数学专业的学生。高中毕业时,乔丹数学属于A档,就算靠成绩也能进北卡。乔丹刚进北卡的时候,选择的是数学专业,到大三的时候为了兼顾打球,才转了专业,到了课程负担没有那么大的文化地理专业。乔丹说过他一直喜欢数学。尤其退役后,他认为他的数学头脑能帮助他打理商务。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
本文是一位老师给他学生的公开信。老师的初衷是想让学生们多学一点,于是在暑期免费开了小平邦彦的《微积分入门》的讨论班。但刚开完一节,有人就顶不住了,纷纷请假。理由无外乎是要打工、旅游、家中事务等。这位老师为了让这个班能继续下去,写下了如下的话。
各位同学:
此时正进入到讲授小平邦彦的《解析入门I》的关键时刻,刚讲完第一节的序言,也就是衔接现有的知识和以后要学的知识的阶段,从1.2开始,严密性和分析性的要求远高于之前我们所学过的知识。一篇序言,我都写出了四篇讲义,那么你们应该想见,在以后的学习中,正文中还有多少知识要我们来思考和学习。而后面的问题,按照我的想法,写出来的讲义是有限的,最重要的是在于你们自己要熟读课文和反复思考。染和酿的效果是不同的,一个是从外到里,用久了会褪色;而另一个是从里到外,越陈越香,我和你们说过,只要你们认真把书读熟了,思考了,哪怕就是你们自己独立思考明白这个书上的一个问题,或者是至少你们知道这本书上有哪些是不明白的,我就能和你们讲清楚。我也告诉过你们,这本书我只会给你们讲前20面,那么就会有两种结果:第一,读明白了,那会有一种自信心爆棚的感觉,这本书我可以靠自己读懂了;第二就是中途学不明白了,那会像垮山一样的崩溃。只要你读明白了前20面,课本上的知识再也没有你学不懂的了,读明白第一章,数学分析能力可以横扫全校,再说远一点,如果能把第一卷读完,那你完全有能力去拿一条板凳,和你们自己的老师坐在同一张桌子上去谈经论道。我还和你们反复说过,真正的高手不是在于参加了多少补习班,也不是在于做了多少难题,而是在于只要把课本读懂,自己就能够把什么问题都想明白,题目可以拿在手里当把玩意。到那个时候,题目的作用不再停留在考验那些知识还没有掌握,而是在于看看哪些问题别人已经想到,而你没有想到。所以必须要你自己去主导题目,而不能让题目来主导你,那样的话,你就是题目的奴隶。

你们似乎很在意考试成绩。你们应该明白,考试是那帮命题人绞尽脑汁弄出来的一批试题,里面总有些题目是新的,那么遇到新的题目时,我们就必须有自己可行、可靠的思维方法去分析和解答它。我曾经说过,技巧不可靠,分析是王道,懒惰最可耻,后悔一辈子。但是我从未说技巧不重要,我说高手可以把题目拿在手里当玩意,但是我也从来没有说过不要做题。究其本意,在于,不管技巧有多花俏,必须以分析作为基础,也就是你必须保证你用了优美的技巧做出来的题,必须是正确的,而不是错误的,如果是错误的,你的技巧再优美,还是得分不到,这就必须以扎实的基础知识,还有清晰明白的分析过程来考察你的解题方法是否正确。然后,在达到高手那个层次之前,要通过做题来巩固知识,做题的过程中要思考,思考这个知识是这么用的同时,也要思考我在读书的时候要怎么展开想象,主动思考,在考题出现之前,就想到这个知识点在此处的应用,从而未雨绸缪。
要达到这个境界,以我现在的眼光来看,除了读小平邦彦的书之外,别无他法。你们听了我的课,看了我写的讲义,就会体会到,这是把课文熟读之后,再思考所获得的成果。那么学习和思考的过程和方法,不限于学习数学,物理、化学、生物,甚至是文科类的课程,依然有适用的空间。你们也许会思忖,同样是一本书,我可以给你们讲得如此深入,那么我肯定是参考了其他的教科书,或者是请教了其他的老师才达到这个样子的,对于这一点,我也不否认,但是你们应当知道,我去参考其他的教材,请教别的老师,这也是一个学习的过程,别人代替不了我,而且最重要的是,当我通过其他途径弄明白一些问题后,再回过头来看时,我发现其实小平邦彦大师已经在他的书上写得清清楚楚了,只是我当时没看明白,没仔细去想而已。这并不是对于小平邦彦的书有所过誉,而是他的书实际就有这么巨大的作用,我还是用极为保守的语言来形容的。
小平邦彦写的教材,从小学的《新算术》,到高中的《新订数学》,再到大学的《解析入门》、《复素解析》、《复素多样体论》,再到研究论文专题文献等,这里没有提到初中的教材,是因为我没有找到小平邦彦写的初中教材,日本曾经用过的初中数学教材是数学家弥永昌吉写的,不过这也不妨,弥永昌吉和小平邦彦在著书上也是一对黄金搭档,合作写过书。作为世界顶级的数学大师,小平邦彦如此倾力于初等数学教育,这是在他所在的层次绝无仅有的,从这个角度上来说,世界上没有人在数学教育的体系性和衔接性上做得比他更好了。
与之相似的还有一个20世纪伟大的苏联数学家,他叫柯尔莫哥洛夫(Kolmogorov),他经常在莫斯科大学主办的全苏数学冬令营中授课,但是你们要知道,莫斯科大学的数学,当年是可以和美国的普林斯顿大学分庭抗礼的,那是世界范围内数学教育和研究最顶尖级的两所名校,苏联学生素以基础扎实,能力强悍,数学物理都能胜任而闻名,他们设有类似于我国艺术专门学校之类的数理专门学校,里面竞争异常激烈,只能用残酷来形容,淘汰率极高。可以想见,能进莫斯科大学冬令营的学生有多强悍。中国在五十年代全面学习苏联,有不少学生到苏联去留学过,但是迄今为止,在莫斯科大学拿到数学博士学位的,仅有三人,一个是已故的著名数学家谷超豪,一个是中科院现任数学研究所所长周向宇,周向宇是八十年代后期,中苏关系缓和之后去苏联留学的。还有一个我不记得名字了,但他早已经不在国内了。那么,在数学基础教育的普及上,小平邦彦做出的贡献有多大,他的著作,是留给人类文明的一大笔宝贵的遗产。

读小平邦彦的书,只要具备最基础的简易逻辑和集合的知识,根本不用再去参考其他的资料,他的书自成体系,却又博大精深,里面的知识环环相扣,你在读书的过程当中,必须把前文的知识真正读明白,才能去学习后面的知识,文中仅有的几个超纲的名词,对于书里知识的理解都不起明显的阻碍作用了。那么,他写的书,都是在尽力让别人思考,而思考以后,都能学明白的。在教学中,小平大师要求学生对基础知识的领悟和应用达到极限的程度,他的书的第一章,实数,其实已经是实分析的基础理论了,实分析是大学数学专业高年级三大分析课之一,还有两门是专门研究复数的复分析和专门研究函数的泛函分析。而小平邦彦大师写的能让读完高一的学生就能看懂。我在很多面对的读者层次远高于《解析入门I》的数学书中看到过本书中所提到的知识点,其他的书当然应当写得比这本书中写得深奥和详细,但是从思想上来说,绝无可能比小平邦彦大师的著作更深邃了,同时也更无可能比小平邦彦大师的著作更精彩了。所以,这本书只要高一读完了,就可以读,本科生可以读,研究生亦可以读,学生应该读,老师更应该读。在读的过程当中,就能得到提高。所以,你不要认为你基础不好,也不要认为你数学思维能力不强,因为我们世人(一般的普通人)的数学基础和能力的差别,在以数学之神的形式而存在的小平邦彦大师的眼里,那就像我们看一只蚂蚁的体长是6.3毫米还是6.25毫米的差别一样,这个差别其实并无实质上的意义,而小平邦彦大师由此就为我们提供了一个适应口径最宽的学习数学的方法,那就是他在晚年,把他毕生所学倾注在一本高中生就可以看懂的解析教材上,我们只要按照正确的方法努力去读,就能读懂,而读懂之后,就会知道怎么去应用,别人能够想到的,你也能想到,甚至很多别人想不到的,你都能想到。从熟读到思考,从思考到应用,再从应用到领悟,这就是“分析是王道”这一句话在这首顺口溜,或者说打油诗中的含义,当你们真正明白这句话的含义时,你们可以感受到,存在于课本上知识,以肉眼可见的形式进入你的头脑里面,然后自动相互作用,相互结构,成体系的表示出来,一个知识点就能照亮它所适用的范围,再遇到所谓的难题,能够像千手观音一般,伸出解决这个问题最娴熟的那只手来轻松应付。
当你拿起这本书的时候,翻开大略浏览一下,也会觉得里面字也是字,纸也是纸,如果你真的深入去品读,越读深入,就越会发现这本书的内涵,当你发现自己在知识和能力上已经收获满满时,这本书还如一潭潇潇清泉,里面的宝藏依然取之不尽用之不竭。
小平邦彦大师已经作古多年,但是,他的思想依然鲜活的存在于他所著的每一本书中,只要认真去读,就能以这本书为窗口,超越时空,聆听这位远去的大师在字里行间对我们以睿智而朴实的方式讲授的知识,握住他那双温暖的大手,他在天国向每一位愿意学好数学的后辈投来期盼的目光,他其实从未远去。
《解析入门》国内翻译的名称是《微积分入门》,在翻译的评价上,我个人觉得略有矛盾,总的来说,语言平和通顺,大方向正确,但是符号的错误还是有一些的,经过仔细思考可以校正一些,我是托人从日本买来原版勘误的。此书曾得到武汉大学前校长,数学家齐民友教授的极力推崇,但是由于种种原因,2008年出版之后,没有再版,应该是知道的人不多,这本旷世经典没有得到应有的崇敬,也没有发挥出应有的价值。希望我写的这篇小文,能告知一些想学好数学的同行者,加入到和我一起呐喊呼吁的行列中来,期盼相关出版社能仔细校勘那些翻译和排版印刷的错误,并积极筹备再版。


在此怀念并感恩小平邦彦大师。
此致
祝大家学业有成。
爱你们的讨论班主讲人
2017.7.10
后记:《解析入门》在日本的出版商为岩波书店,这是一家有百余年历史的著名书店,在工具辞书,自然科学书籍和社会科学书籍的出版领域享有盛誉,这家出版社尊重中国的主权和领土完整,出版物中承认一个中国,台湾是中国的一个省。首任社长岩波茂雄先生曾致力于推动中日之间的文化交流,在日本侵华战争期间,尽力倡导反战运动,向中国赠书的计划也因战争而隔断,他的继任者于1947年开始继承他的遗志,向中国赠书并延续至今。除了促进中日的文化交流外,也打开了两国互赠图书的良好风气。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
高考完了要填志愿?有点动心想考数学专业,又担心这个专业不是自己的菜?担心这个专业太难,太枯燥,就业前景黯淡?你现在需要改变对数学系的“典型”成见,并重新建立对数学专业的认知。
误解1: 数学系的人都是不食人间烟火的神仙。
总是有一些人会不断向你强调,数学系的人就像《生活大爆炸》里的谢耳朵那样神一般的存在。但是,我要告诉你的是,大部分数学系的人都是普通人,他们只是对数学有偏爱而已。

不是所有数学系的人都戴眼镜,他们也不会走到哪里身上都揣着计算器,他们更不会只穿纯白T恤和格子衫。数学学科很容易和其他学科结合起来,这些学科包括艺术、科学、语言,甚至历史学习中都可以加入数学。所以,你得抛弃成见,并不是每一个数学系的人都是你想的那样,神仙一样的人。
误解2:如果你数学系毕业,你只能去当老师。
这完全就是胡说八道。数学系的毕业生是解决问题的好手,那意味着在诸多领域和几乎任何职位,数学系的毕业生都能胜任。是的,通过职业培训,你可以去数钱(成为会计,笑)。但是,你同样可以为保险公司工作,编写程序为某个保险产品的精算赔率。数学专业的就业有着真正的无限可能性,所以你不要在这种思想阴影下认为自己大学生涯里必须掌握教学方面的技能。

误解3: 所有的数学专业都一样的,因为他们只和数字打交道。
实际上,每个数学专业方向都不一样。有的方向和现实应用结合很紧,有的则只是和纯代数打交道。任何人在数学系里都能找到你感兴趣的课程,无论你只是对Excel和统计感兴趣,还是对工程应用或者玩游戏(博弈论,game theory,再笑)感兴趣。奥,数字只是我们日常使用的冰山一角。16进制数、希腊字母,还有大部分英文字母我们都在用,不仅仅是x和y。

误解4: 只有男生适合数学专业。
根据《卫报》的统计,42%的英国数学专业毕业生是妹子。在中国,一些学校数学专业的女生也比男生多,尤其一些师范类的数学专业。所以,在你选的课程之中,有相当比例的老师可能是美女老师。同样,你的数学系同学中也有不少女同学每天和数据分析和微分方程打交道。

误解5: 数学系的人都是心算大神!
一些人可能因为掌握了一些计算技巧在心算的时候可能真的很快。但我打赌,在你的周围朋友中,没几个能在10秒内心算出6432 ÷ 17的结果(结果是378.353……)。数学系的人也是普通人,也严重依赖计算器计算这些结果。他们不都是能背出30以内乘法表的神仙。

误解6:从数学系毕业,太难太难了。
如果到了毕业,你还只是会识数、简单统计、简单代数这种小学阶段的数学,那么你就不在我的讨论范围。毕竟,在任何专业 你想学到知识与技能都必须有足够多的付出,这样才能顺利毕业。但你不必担心数学专业的毕业问题。数学专业又不会咬死你。

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
今年8月,四年一届的国际数学家大会将再巴西里约热内卢举办。这次大会除了会组织最高级别的学术讨论,还会有很多公众级别的普及活动。
大会总结很多历史上数学家、科学家关于数学的名言。这些名言,我们哆嗒数学网的小编整理了一个150秒左右的视频,供大家欣赏。我们可以看看,在这些大咖眼里,数学到底是个什么样子。
lt is impossible to be a mathematician without being a poet in soul.
——Sofia Kovalevskaya
数学家的灵魂深处,必住着一位诗人。
——柯瓦列夫斯卡娅
A mathematician is a device for turing coffee into theorems.
——Paul Erdos
数学家就是把咖啡转化成定理的机器。
——埃尔德什
Mathematics is a game played according to certain simple rules with meaningless marks on pape.
——David Hilbert
数学是根据简明规则把玩纯粹符号的纸上游戏。
——希尔伯特

Remember to look up at the stars and not down at your feet.
——Stephen Hawking
要记得抬头仰望星空,而不是低头只看着你的脚下。
——霍金
In math, you're either right or you're wrong.
——Katherine Johnson
数学里,非对即错。
——凯瑟琳·约翰逊
Mathematics is the music of reason.
——James Joseph Sylvester
数学是推理的乐章。
——约瑟夫·西尔维斯特
Genius is patience.
——Isaac Newton
天才在于持之以恒。
——牛顿
Mathematics is not only real, but it is the only reality.
——Martin Gardner
数学不仅仅是真实的,还是唯一的实在。
——马丁·加德纳
Beauty is the first test:there is no permanent place in the world for ugly mathematics.
——Godfrey Harold Hardy
美是数学的第一重考验,丑陋的数学在这世界上没有永驻之地。
——哈代

Pure mathematics is, in its way, the poetry of logical ideas.
——Albert Einstein
纯数学,究其本质,是逻辑思想的诗篇。
——爱因斯坦
Mathematics is the most beautiful and most powerful creation of the human spirit.
——Stefan Banach
数学是人类精神中最美丽最强大的创造。
——巴拿赫
If only I had the theorems! Then I should find the proofs easily enough.
——Bernhard Riemann
要是我知道定理是什么就好了!这样证明过程就容易多了!
——黎曼
Number rules the universe.
——Pythagore
数统治者宇宙.
——毕达哥拉斯

Where there is matter, there is geometry.
——Johannes Kepler
有物质的地方,就有几何学!
——开普勒
The essence of mathematics lies in its freedom.
——Georg Cantor
数学的本质在于它的自由。
——康托
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,AskaMathematician网站。
翻译作者,radium,哆嗒数学网翻译组成员。
校对,Math001。
注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
最初的问题是:......让我感到困惑的是一些像巴拿赫-塔斯基悖论(又称“分球怪论”)以及其他在纯数学和理论物理中抽象的概念,都可以认为是已经“被证明”的。那岂不是违反了在真实/物理世界中只能通过实验来验证假设,从而证明某件事情的原则? 即使如此,说任何事情都可以毫无疑问地证明是不是有点不太合理?

物理学家:假设检验是科学探究的主力,用于决定假设成立可能性的大小。假设检验的结果不是承认,也不是否认的结果。是一个估计你会不小心看到给定结果的可能性。发生意外的可能性越小,它就越有可能成为真正的影响。 例如,我们还没有证明希格斯玻色子存在,只是因为CERN的数据偶然会产生一兆分之一的概率。 这不是一个证明。 即便如此,如果一个现象按照预测的方式运行,那么你也可以相信它是真实的。
事情“被证明”是确实可靠的,就像我们可以肯定地知道有人赢得了一场国际象棋比赛一样。 宇宙结构中没有任何东西可以决定棋子在棋盘上移动的方式(除了自然的变化)或谁赢了某场比赛,然而每个了解这些规则的人都可以成为胜利者。而数学,基本上就和国际象棋或其他游戏的规则差不多(虽然看似自己玩自己的,但它是最纯粹的科学,它以最简单的思想让我们摆脱对事物模糊的把控)。
一旦规则被建立,你就可以基于这些规则和一些逻辑证明一些事情(技术上讲,逻辑只是更多的规则)。例如,基于直接了当数学规则的合理简短列表,您可以首先定义素数是什么,然后证明它们的数量是无限的。
数学中的规则被称为“公理”而基于这些规则的结果被称为“定理”。例如,“你不能将一个点分成两半”这是一个公理,与此同时“有无限多的质数”是一个定理。当你第一次了解到数论和算法时,你会学到皮亚诺公理(Peano's axioms)以及基很多定义和基于这些定义的结论。就像下棋的规则一样,公理规定了在数学中你能做和不能做的事,从中人们可以自由地去探究他们可以或不可以得到的结论。数学没必要让得到的结论都来自于实际,因此它恰好包括了一些利用最有效的工具去理解它所构造的事物。
事实上,我们没有根据实际生活创造的数学似乎看起来没有价值,但结果常常是这些数学却变得相当的有用。例如,通过将几何学的规律从三角形,三维空间甚至距离概念中推广出来,数学家为爱因斯坦的广义相对论铺平了道路(它描述了在扭曲时空方面引力的性质)。基本上,他仅仅是把他关于时空的想法用数学上早就创造出的结论表达了出来。

巴拿赫塔尔斯基分球悖论在集合论中已经存在了一个世纪之久了。他说的是你可以(除了其他因素外)把一个球分成五个或更多的集合,旋转然后移动一些集合,然后重新组合它们可以得到和最初一样大小的两个球。这些集合不像块拼图碎片,更像雾中的水滴,几乎所有的这些集合都小于给定尺寸。值得注意的是,这些在现实生活中是完全不可能的。分球怪论托了数学的福,它不被现实的严格限制所主宰。
巴拿赫塔尔斯基分球悖论基于集合论中一般的公理,策梅罗-弗兰克尔(Zermelo–Fraenkel,简称ZF),但是需要增加一个具有争议的公理,即“选择公理”(ZFC)。在数学界,“具有争议”的是似乎有点用词不当;数学家们大多时候都在自顾自的写长篇论文,如果需要打断写作而交流,他们只会悻悻地相互打量一下。选择的公理对于数学,就像吃过路兵对于国际象棋一样,当它被需要时,它就出现了,但是你一般不需要它(设想你曾经在下国际象棋时被人吃了过路兵,但你并不知道具体它是什么)。
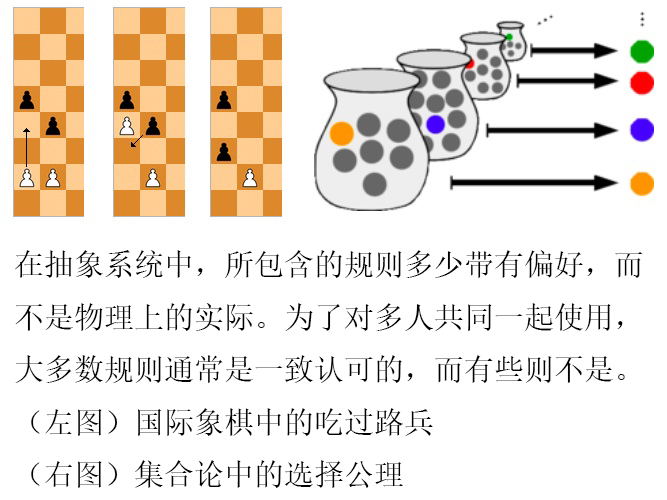
选择公理说的是你总是可以从无限多个集合中在每个集合里取出一个元素。如果集合只有有限个这是显然的(“放手去做就行了”),或者你可以提出一个合适的规则将这样的元素取出来(例如“每个集合中取最小的数”)。但是有时你会遇到无限个集合中的无限个元素。没有最大、最小甚至中间的元素。如果你想知道如何从这些集合中挑选一个唯一的元素,选择的公理说“大哥,稳,你可以的”。这是被提出来改变游戏规则的一个完整的陈述。这不是真的或假的问题,而是数学家与其他数学家之间一致统一以及和睦相处的问题。
物理学,尽管是科学的女王,我们凡人可以努力理解现实本质的手段,也不比数学好。在物理学中,你可以“证明”事物会发生或不会发生,但仅仅是基于已建立的规则:“物理定律”。例如牛顿万有引力定律说,两个相距为r,质量分别为M和m的物体间的吸引力为F=GMm/r²。不仅仅是一个事实的陈述,像这样的数学表达式允许我们精确地描述或预测事物的物理行为。根据这个定律(和其他一些)我们可以精确地证明轨道是椭圆的。注意到“精确”,但不一定是“真的”。
如果这些规则被实验证明是错误的,那么基于它们的证明不是真正的证明。这就是为什么物理学家如此小心地建立和验证他们的理论的每一个细节。他们花费了(似乎浪费了)几十年的时间来测试他们已经几乎100%确定的东西。因为任何基本定律的缺陷都会波及到基于它的每一个“被证明”的事物。
数学或物理学中的一些基本规则或假设被颠覆了。在数学中,这完全是由于逻辑,但是物理要求得更多。我们不能仅仅用逻辑来推测宇宙的规则。如果你只是用头脑空想,这个宇宙的本质将是对你一个真正的冲击。无论你有多聪明,你都需要实验和观察来了解关于世界的新事物。
很容易(是的.......很容易)写下一些物理规律,这些规律似乎描述了我们对宇宙的了解,但结果却是错误的。 如果没有大量精确的数据和数学来支撑它,就没有办法知道你知道的东西仅仅只是你的想法。牛顿定律是非常有用的,但最终被证明和现实也不是完全贴合的。他们根据我们当时的数据完美地描述了宇宙;当更准确(更难以获得)的数据产生“更真实”的物理理论时,我们开始意识到牛顿的物理学是仅仅只是非常好的近似值。
在爱因斯坦之前,我们已经习以为常地认为时间和空间是完全独立的。它采取了一些严肃的深奥的现象(例如,光速的不变性和水星轨道上的微小误差),表明时间和空间是相互关联的,它们是同一事物的不同方面。在贝尔之前,人们几乎完全笃信,无论我们是否知道这个状态是什么样的,认为一切都是在一个明确的状态下进行的,这个看似完全合理的假设就是“现实主义”。
同样,我们认为的宇宙和我们目前触及到的宇宙的差异(可能)是一组不可思议的深奥的、几乎不可察觉的效应(例如,放射性衰变和纠缠粒子的“不可能”统计数据的随机性)。这些效应花了很多精确的实验去验证(尽职检查,阐述,并多次验证)以及利用数学得出结论:不,一个如此基本的假设,我们称之为“现实主义”或“现实假设”实际上是错误的。量子物理学家已经超越了通常的理解,他们将这个性质定义为“单一状态”的“反事实确定性”(counterfactual definiteness)。这没什么好说的,但是如果你能看懂,你很厉害。很好。
在数学中,虽然你可以证明一些东西,但是最终就像棋局,你仅仅只是在棋盘上移动棋子。在逻辑领域里有很多东西需要理解和发现,但是数学,和所有人类的抽象思考一样,全都存在于我们的头脑中。
在物理学中,你不仅可以用物理定律来证明事物,而且那些物理定律是唯一真实的,因为它们总是在每一个场景中完美成立(我们可以测量和验证),就是说,你可以放心的相信他们。
注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
高盛集团作为金融巨头,每到世界杯开赛前就会给出一个世界杯赛过的预测。近日,在其网站上发表了一篇题为《世界杯与经济2018》的报告(The World Cup and Economics 2018)的文章,文章中对2018的世界杯的比赛进行了预测。
高盛的研究员构造了一个统计模型用来模拟生成2018世界杯的所有比赛结果。相比于2014年用主要回归分析的办法,这次而用于预测的方法,用了更多的机器学习的技术。按高盛文章的说法,从解释效力来说,新的预测模型是之前基于泊松过程理论基础预测模型的精度的五倍。
高盛的模型中的变量:
1、队伍水平评分,量化队伍的能力,主要依据历史战绩。占40%
2、队员水平评分,量化队伍中队员的个人了,主要依据俱乐部的成绩和表现。占25%
3、最近比赛的成绩。占10%。
4、最近重要比赛的成绩。占10%。
5、最近比赛的得失球情况。占5%。
64场比赛的比赛情况的模拟,用暴力的蒙特卡罗方法,模拟了10万次。
高盛的一些主要结果:
1、 巴西将再7月15号的决赛中战胜德国,第6次捧起大力神杯。

2、 法国的夺冠概率高于德国,但不幸的事情是,他们将与巴西提前在半决赛相遇。这意味着半决赛是“提前的决赛”。
3、 16强中有10只欧洲队、4只南美球队、1支中北美球队、1只亚洲球队。这只亚洲队是沙特阿拉伯。
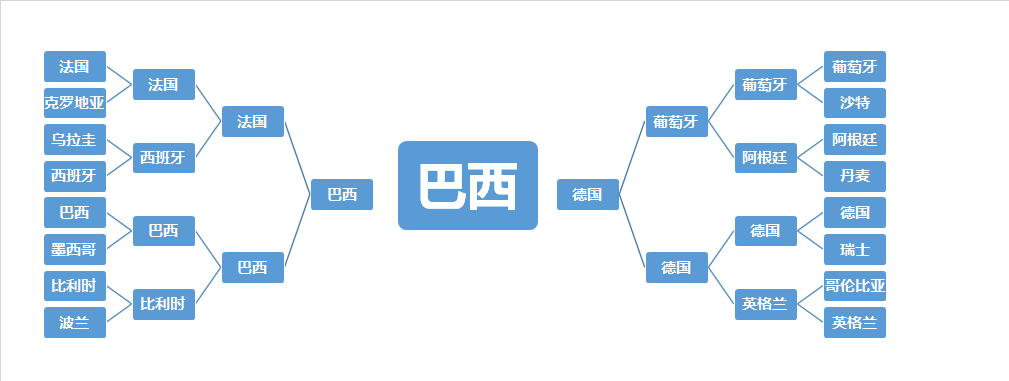
4、 巴西、德国、法国、葡萄牙成为最终的四强。
5、 英德大战会在7月7日的八强战举行,德国是胜利者。
6、 梅西领衔阿根廷队止步八强,梅西世界杯之梦渺茫。
7、 东道主俄罗斯虽有主场之利,但16强都进不了。
不过,高盛没有把所有的预测认为必然的,他同时给出了事件发生的概率。
比如,即便认为巴西会夺冠,但预测模型中,巴西夺冠的概率为18.5%,不到两成,第二名法国11.3%,第三名德国10.7%。而亚洲球队中,虽然沙特阿拉伯出现在了16强对阵表中,但模型给出的沙特阿拉伯进入16强的概率36.5%,低于澳大利亚的的49.8%。
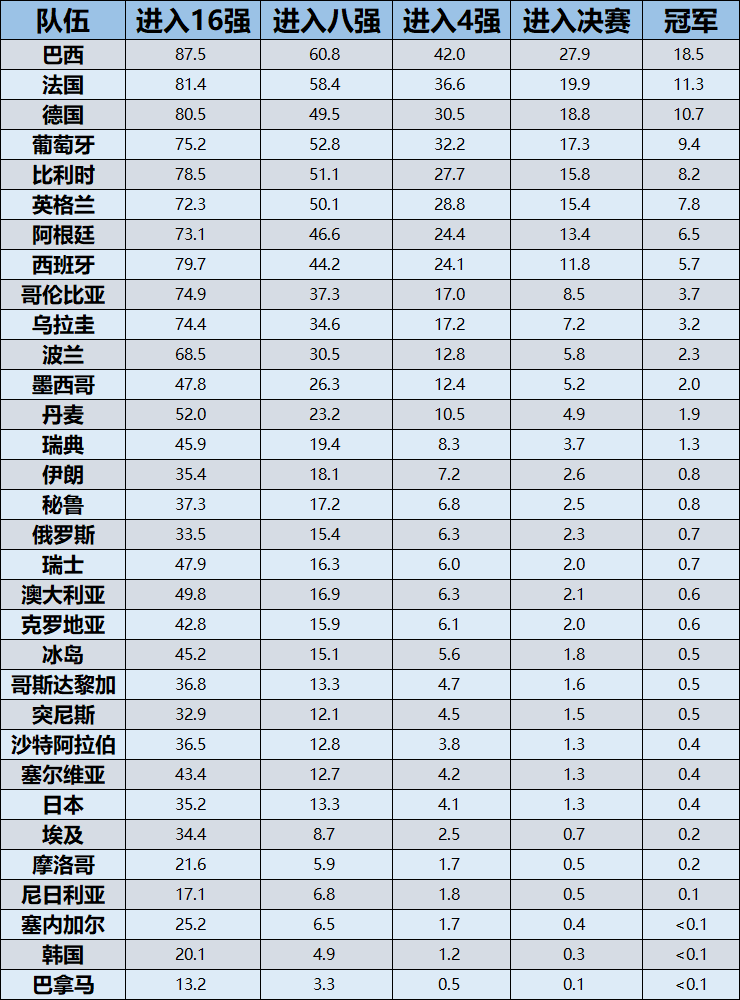
另外,有的预测结果非常诡异。比如A组比赛的结果是,乌拉圭两胜一平积7分,那个平局是和沙特,然后剩下比赛全部平局,于是沙特3分,俄罗斯和埃及都2分,沙特出线。
注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
原文作者,Mark Oliver。
翻译作者,math我想想,哆嗒数学网翻译组成员。
校对,小米。
毕达哥拉斯,这个毕达哥拉斯定理背后的人不仅仅是一个数学家。毕达哥拉斯的追随者们认为他是上天派下来的,并且尊其为精神领袖。对毕达哥拉斯学派来说,数学是一种宗教体验,而有些方程式是神圣的秘密,不宜为普通人所知道。
当你的中学老师教你如何求出直角三角形的斜边长时,你可能不会跪下来把他当作神来崇拜。但是,当它第一次在古希腊发生时,这却是很多人的反应。
在这个想出如何计算三角形边长的男人背后是一个完整的教派而且正如你所想象的那样,他们有一些非常奇怪的信仰。
10.毕达哥拉斯派崇拜数字
.
毕达哥拉斯有很多追随者。 一大批数学家报名成为他的学生,学习他所知道的一切,帮助他解决宇宙的伟大奥秘。这不仅仅是一群喜欢数学的人,他们成为了一个完整的教派。
毕达哥拉斯相信,数是万物的本质。他教导他的追随者说,世界由数的和谐所控,它们构成了现实的每一部分。不仅如此,他还认为这些数字几乎像神一样非常神圣。
毕达哥拉斯学派中有几个神圣的数字。7代表智慧,8代表正义,10是所有数字中最神圣的。数学的方方面都是神圣的。每当他们解决了一个新的数学定理,他们就会杀一头牛来表示对神的感谢。
希腊人认为这有点怪异。 他们不把它称为哲学或宗教,而认为这是一种邪教,一种危险的东西。毕达哥拉斯吓坏了人们。为此,人们甚至烧毁了他的房子,把他赶出城市,担心他对神圣数字的神秘控制。
9.毕达哥拉斯学派向数字10祈祷
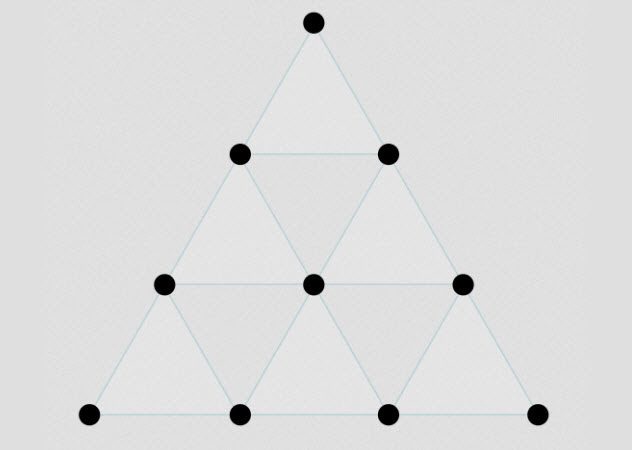
毕达哥拉斯学派有一个神圣的图形标志,被称为圣十(Tetractys)。这是一个三角形,横跨四行十个点,象征着空间和宇宙的组织。他们认为10是具有最高秩序的数字,其中包含所有凡间事物的过程。他们是真正的崇拜它。
毕达哥拉斯的追随者们有一套专门用来崇奉数字10的祷文——“祝福我们,神圣的数字,你们产生了神和人!因为神圣的数字始于深奥而纯粹的统一,直到到达神圣的4。之后它就会成为万物之母,包括所有人,所有土地,最初产生、永不改变的、永远不会疲倦的神圣的数字10,一切事物的拥有者。”
如果想加入毕达哥拉斯派系,每个人都必须对圣三角宣誓。他们会以“纯粹的,圣洁的,四字的名字”的名义宣誓他们的忠诚,也就是圣十。然后他们必须支持毕达哥拉斯,他像是数学界的普罗米修斯,给人类带来了圣十。
8.毕达哥拉斯被当作神

毕达哥拉斯的追随者认为毕达哥拉斯是半神半人,因此称他为“圣人毕达哥拉斯”,并且告诉人们他是神的儿子——通常是赫尔墨斯或阿波罗,这取决于你向谁发出指令。
他们甚至有赞美诗来歌颂毕达哥拉斯的神性。一首歌这样唱到:“皮塞斯,萨米安部落最美丽的母亲,太阳神阿波罗怀抱着她。于是,光芒万丈的毕达哥拉斯来到世上——他是宙斯最亲近的人!”
他们甚至还认为毕达哥拉斯有超自然的力量。他的追随者们说,他可以通过抚摸鹰和熊来驯服它们。他只需要用声音用可以控制任何动物,并且他有能力在月亮上写字。
关于毕达哥拉斯最大的传说之一莫过于他黄金大腿。当有人对他的神性产生怀疑的时候,据说他就会给对方看自己黄金大腿,随后立马会得到对方的敬仰。在一个故事中,他向阿波罗的大祭司展示了自己的黄金大腿,作为奖励,他得到了一个富有神力的金箭,让他可以飞越山脉,驱赶疾病,平息风暴。
7.他告诉人们他可以在死后不断转世

人们开始编造一些关于毕达哥拉斯 的故事,不仅仅是因为斜边长定理的发现激起了人们对他的崇拜风潮,同时因为毕达哥拉斯本身也鼓励别人去这么做。他直接告诉人们,他是神的儿子,经多次转世,直到他现在的样子。
毕达哥拉斯宣称,在过去的生活中,他是赫耳墨斯的儿子,除了不朽之外赫尔墨斯还给毕达哥拉斯提供了他想要的一切天赋。毕达哥拉斯要求保留他每一段人生的记忆,现在可以记住他曾经的每一世。他曾经在特洛伊战争中与阿喀琉斯进行过战斗。他曾经当过卑微的渔夫。他甚至曾经是一个和权贵上床的名妓。
不仅如此,毕达哥拉斯还声称他可以用新的身体来感知旧灵魂。传说他曾经看到一条狗在街上遭到殴打,赶紧跑来阻止。“住手!别打它!”毕达哥拉斯大叫 “这是我朋友的灵魂。”他在狗的吠叫中认出了朋友的声音。
6.他是最早的也是最懒惰的素食主义者之一

在西方历史中,最初有一批人因为道德的原因开始吃素,毕达哥拉斯便是其中之一。他告诉他的追随者们吃死去的肉食会污染自己的身体,他们也因此不会杀生。
不过,他的原则有点奇怪。你可能记得我们之前提到过他会杀牛,同时也是素食主义者。就像一个吃鱼肉和鸡肉的素食主义者,毕达哥拉斯的素食主义不是特别的严格。
希腊作家第欧根尼在毕达哥拉斯的传记中写道:“他所做的祭品总是无生命的。”接着,提奥奇尼斯澄清道:“尽管有人说他会提供公鸡,还在吃奶的小山羊和猪。”不过,毕达哥拉斯还是有清楚的底线。“但是羊羔,”第欧根尼解释说,“从来没有!”
在希腊人看来,希腊人对毕达哥拉斯的原则和我们对希腊人的感觉一样怪异。在他的时代,希腊人散布了一个关于一个坚持说从来不吃任何活物的毕达哥拉斯人的笑话。但在被抓到吃狗肉后,这个人说:“我是吃了,但是我先杀了它们,所以它们不再是活物了。”
5.他的教条涉及方方面面

毕达哥拉斯学派的人可能在食肉问题上不太严谨,可是这并不意味着他们可以做任何他们想做的事情。他们在任何事情上都有近乎难以置信的严格的特殊的教条——例如规定了必须先穿哪一只鞋子。
“必须要先穿右脚的鞋子”,他告诉自己的追随者们。一旦你穿上了鞋子,他会继续说:“你不能在公共的道路上走路。”不过,他的规矩不仅限于鞋子。在关于掉在地上的食物的五秒原则问题上,他告诉他的追随者们永远不要去吃在掉下饭桌的食物。
他对性行为也有特别严格的规定。毕达哥拉斯认为,体液是男人灵魂的一部分。当男人失去一些体液,就仿佛是放弃了他们的一些力量。毕达哥拉斯的追随者们被教导尽可能避免性行为。但是如果他们控制不住,毕达哥拉斯告诉他们:“在冬天可以享受性行为带来的乐趣,但夏天,必须戒除。”
4.新入教的人五年不能说话

毕达哥拉斯认为保持沉默十分重要,保持安静是一个学习自我控制的方法,所以他确保每个想加入他的教派的人都要这样做。任何报名加入的人都必须连续保持五年不说话。
这部分是为了帮助人们保持纯洁,但是,有很多理由让我们相信,这与确保他们保守秘密有关。即使在古希腊,把自己称为神的儿子并让人们崇拜数字的人,不是一个标准的模范公民。
毕达哥拉斯教派的人尽力保持生活安静。所以,除非这个人可以证明自己可以保持沉默,否则他们不会让任何人进入他们教派。
然而,大多数希腊人并不了解这些沉默的侍从的深层含义。 希腊人只是很高兴成为毕达哥拉斯追随者后,因这个改变而不用谈论数字。一般来说,安静的人比话多的人更加令人印象深刻。
3.他可能淹死了一个发现无理数的人

西帕索斯是毕达哥拉斯最有名的追随者之一,传说他是第一个发现无理数的人,而且他可能因此而死。
西帕索斯给出了二是一个无限不循环的无理数的证明。这不仅仅是一个重大的发现,更是一个公开的反叛。毕达哥拉斯曾经教导说,所有的数字都可以表示为整数与整数的比例,而西帕索斯已经证明他的神圣的教主是错误的。
根据传说,当时他俩在一条船上,西帕索斯给毕达哥拉斯看了他的证明,然而,毕达哥拉斯抓住了西帕索斯,并把他摔到船边,把他的头按到水里,直到他不能动弹。然后毕达哥拉斯把尸体扔到船上,转向船上的其他人,并警告他们永远不要告诉别人发生了什么事。
这个故事可能不是事实,它更像是一个毕达哥拉斯寓言故事的扭曲版本,说西帕索斯被神淹死,作为向世界揭露无理数的秘密的惩罚。
但是这个故事仍然揭露了毕达哥拉斯派的一些令人胆寒的事情。他们把这个故事作为一个寓言传播给人们,告诉他的追随者们,如果他们与世界分享教派的秘密,等待他们的可能就是一个浸水的坟墓。
2.毕达哥拉斯演讲时总待在一个帘子后面

毕达哥拉斯派中有两种人:数学家和声闻家。数学家是毕达哥拉斯最亲密也是最值得信赖的追随者。他会亲自见面,并详细向他们解释他的定理。他们被允许知道隐藏在世界其他地方的先进数学的秘密。
当然他们不得不为这个特权付出沉重的代价。要成为一个数学家,一个人不得不放弃肉类,女性和所有的私人财产。从此以后,他们唯一的忠诚就是毕达哥拉斯了。
其余的人被允许成为声闻家,他们从未被允许看见毕达哥拉斯的脸。当他对他们说话时,毕达哥拉斯将隐藏一个面纱背后,像是奥兹国的法师一样。他不会向声闻家仔细地解释问题,他们只被要求遵循他的仪式。高端数学的危险秘密是不会告诉他们的。
1.他为了不伤害豆子而付出了生命的代价

毕达哥拉斯最奇怪的教规之一是他的追随者们永远不能触碰豆子。他教导说豆子会带走一部分灵魂。他解释说“它们会导致胀气,当气体出来时,会带走人的大部分灵气。”
不仅仅如此。据说他相信豆类包含了死者的灵魂,并告诉他的追随者,“吃豆子等同于啃食父母的人头。”
豆子对毕达哥拉斯派是如此神圣,以至于毕达哥拉斯愿意用生命去保护它们。 据说,一个人因为看不见毕达哥拉斯感到愤怒,就把毕达哥拉斯的房子烧掉了,这时毕达哥拉斯已经危在旦夕。
他为了活下去,他只能不停的逃跑,却在一块豆子田之前停了下来。他宣称,他宁可死,也不愿踩一颗豆子。 最后他让那个人割了自己喉咙这样豆子就能够活下去。
当然,这只是关于他死亡的许多故事之一。 但几乎所有的故事都是毕达哥拉斯死于保护豆田。在一些故事中,他因为试图推翻政府而受到攻击。而在另一些故事里,他被烧死了。但几乎在每一个故事中,毕达哥拉斯都是为了不践踏豆子而付出了自己的生命。
注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 【大结局】数学上下三万年(八):二十世纪下半叶的数学
二战结束,和平与发展成为世界主题。计算机的广泛使用让世界逐步进入信息时代。
本期出场人物有:塞尔、霍奇、柯尔莫哥洛夫、米尔诺、斯梅尔、索伯列夫、邦别里、科恩、格罗腾迪克、阿蒂亚、森重文、康威、瑟斯顿、曼德博、唐纳森、孔涅、怀尔斯、威腾、朗兰兹等。
中国人或华人也有陈景润、丘成桐、王秋冬登场。
本系列下面是往期内容:
1950年
卡尔纳普(Carnap)出版了《概率的逻辑基础》(Logical Foundations of Probability)。
1950年
汉明(Hamming)发表了关于误差检测与误差校正编码的基础论文。
1950年
霍奇(Hodge)提出了关于射影代数簇的“霍奇猜想”。
1951年
塞尔(Serre)利用谱序列来研究纤维丛的纤维、全空间和底空间的同调群的关系。这使得他发现了空间的同调群与同伦群之间的基本关联,并证明了球面同伦群的重要结果。
1952年
霍尔曼德尔(Hörmander)开始了偏微分方程理论的工作。十年后他因为这项工作获得菲尔兹奖。
1954年
塞尔(Serre)由于他的谱序列的工作以及层的复变理论的工作获得了菲尔兹奖。
1954年
柯尔莫哥洛夫发表了关于动力系统的第二篇论文。这标志着KAM-理论的开始,这个理论的名字来源于柯尔莫哥洛夫(Kolmogorov)、阿诺尔德(Arnold)与莫泽(Moser)。
1955年
嘉当(Cartan)与艾伦伯格(Eilenberg)发展了同调代数,将强大的代数方法与拓扑方法关联起来。
1955年
诺维科夫(Novikov)证明了群的字问题不可解。
1955年
谷山丰(Taniyama)提出了关于椭圆曲线的猜想,将在费马大定理的证明中起到重要作用。
1956年
米尔诺(Milnor)出版了《论同胚于7维球面的流形》(On manifolds homeomorphic to the 7-sphere),打开了微分拓扑的新领域。
1957年
柯尔莫哥洛夫解决了“希尔伯特第13问题”,它是关于某些3变量连续函数不能被表为2变量连续函数的问题。
1958年
托姆(Thom)由于拓扑学的工作获得菲尔兹奖,特别是有关示性类、配边理论和”托姆横截理论”。
1959年
布恩(Boone)证明了群的许多判定问题不可解。
1959年
马歇尔·赫尔(Marshall Hall)出版了他的著名教科书《群论》(Theory of Groups)。
1960年
铃木通夫(Michio Suzuki)发现了有限单群的新的无穷族。
1961年
爱德华·洛仑兹(Edward Lorenz)发现了一个具有混沌现象的简单数学系统。它导致了被广泛应用的混沌理论的新数学。
1961年
斯梅尔(Smale)证明了n > 4的高维庞加莱猜想,即同伦等价于n维球面的n维闭流形必定是n维球面。
1962年
雅各布森(Jacobson)出版了他的经典教科书《李代数》(Lie algebras)。
1962年
索伯列夫(Sobolev)出版了《泛函分析在数学物理的应用》(Applications of Functional Analysis in Mathematical Physics)。
1963年
约翰·汤普森(John Thompson)与费特(Feit)发表了《奇数阶群的可解性》(Solvability of Groups of Odd Order),证明了所有非阿贝尔有限单群都是偶数阶群。他们的论文用了250页来证明这个定理。
1963年
科恩(Cohen)证明了选择公理与连续统假设的独立性。
1964年
广中平佑(Hironaka)解决了代数簇上有关奇点消解的一个重要问题。
1965年
谢尔盖·彼得罗维奇·诺维科夫(Sergi Novikov)关于微分拓扑的工作,特别是计算稳定同伦群与分类光滑单连通流形,导致他作出“诺维科夫猜想”。
1965年
邦别里(Bombieri)利用他改进的大筛法证明了关于算术级数的素数分布的“邦别里中值定理”。
1965年
杜奇(Tukey)与库利(Cooley)发表了一篇论文,介绍了快速傅立叶变换算法。
1965年
塞尔顿(Selten)发表了区分在预测博弈结果时的合理决策与不合理决策的重要工作。它导致了1994年的诺贝尔奖。
1966年
格罗腾迪克(Grothendieck)由于他在几何、数论、拓扑与复分析的工作厄尔获得了菲尔兹奖。他的概型理论使得韦伊的几个数论猜想得以解决。他的拓子理论与数理逻辑高度相关,他给出了黎曼-罗赫定理的代数证明,并给出了曲线基本群的代数定义。

1966年
兰德尔(Lander)与帕金(Parkin)利用计算机寻找欧拉猜想的反例。他们找到了27^5 + 84^5 + 110^5 + 133^5 = 144^5。
1966年
艾伦·贝克(Alan Baker)证明了“格尔丰德猜想”,它是关于有理数域上代数数的线性独立性。
1967年
阿蒂亚(Atiyah)发表了《K理论》(K-theory),详述了他关于K理论的工作和指标定理,而之前此工作让他获得了1966年的菲尔兹奖。
1968年
诺维科夫(Novikov)与阿迪安(Adian)联合发表了一个证明,证明了对于d > 1与n > 4380,伯恩赛德群B(d, n)是无限的。
1969年
康威(Conway)发表了他的新的零散有限单群的发现。
1970年
艾伦·贝克(Alan Baker)由于他在丢番图方程的工作获得菲尔兹奖。
1970年
马季亚谢维奇(Matiyasevich)证明了“希尔伯特第10问题”不可解,即没有通用方法判定一个多项式方程是否有整数解。
1971年
史蒂芬·库克(Stephen Cook)提出了有关多项式时间算法的P vs NP问题。
1972年
托姆(Thom)发表了《结构稳定性与形态发生学》(Structural Stability and Morphogenesis),解释了突变理论。这个理论研究了渐变力导致突变的情况,在光学与生物学有重要应用。
1972年
奎伦(Quillen)阐述了高阶代数K理论,它是一个新工具,使用几何与拓扑的方法与思想来描述与解决代数中的重要问题,特别是环论与模论。
1973年
德林(Deligne)证明了三个“韦伊猜想”。
1973年
陈景润证明了每个充分大的偶数可表为一个素数与一个不超过两个素数的乘积之和。它是对哥德巴赫猜想的重要贡献。

1974年
芒福德(Mumford)由于代数簇的工作获得菲尔兹奖。
1975年
费根鲍姆(Feigenbaum)发现了一个新的常数,约等于4.669201609102...,它涉及倍周期分岔,在混沌理论中起着重要作用。
1975年
曼德博(Mandelbrot)出版了《分形学:形态,概率和维度》(Les objets fractals, forme, hasard et dimension),描述了分形理论。
1976年,拉卡托什(Lakatos)的著作《证明与反驳》(Proofs and Refutations)在他去世两年后发表。首次在1963-64年分4部分发表,这部著作给出了拉卡托什关于数学如何发展的阐述。
1976年
瑟斯顿(Thurston)由于他在叶状结构(Foliations)的工作获得美国数学会韦伯伦几何学奖。
1976年
阿佩尔(Appel)与哈肯(Haken)使用1200小时的计算机时间检验了大约1500个构型证明了四色定理为真。
1977年
阿德曼(Adleman)、李维斯特(Rivest)和萨莫尔(Shamir)引入了公钥编码,它是一个用于传递秘密消息的系统,使用大素数和一个公开密钥。
1978年
费夫曼(Fefferman)由于他在偏微分方程、傅立叶分析,特别是收敛性、乘数算子、发散性、奇异积分与“哈代空间”的工作获得菲尔兹奖。
1978年
森重文(Mori)证明了“哈茨霍恩猜想”,即射影空间是具有丰富切丛的唯一光滑完备代数簇。
1979年
孔涅(Connes)出版了关于非交换积分理论的著作。
1980年
有限单群的分类完成。
1982年
曼德博(Mandelbrot)出版了《自然的分形几何》(The fractal geometry of nature),比1975年的工作更完整地发展了他的分形几何理论。
1982年
弗里德曼(Freedman)证明了同伦等价于4维球面的4维闭流形必定是4维球面。这是在1961年斯梅尔的工作之后证明了高维庞加莱猜想的进一步情形。
1982年
丘成桐(Shing-Tung Yau)由于他对偏微分方程、代数几何中的卡拉比猜想、广义相对论的正质量猜想以及实与复蒙日-安培方程的贡献获得菲尔兹奖。

1983年
唐纳森(Donaldson)出版了《自对偶连接与光滑4维流形的拓扑》(Self-dual connections and the topology of smooth 4-manifolds),导致了关于4维流形几何的全新思想。
1983年
法尔廷斯(Faltings)证明了“莫德尔猜想”。他证明了对任意充分大的n,最多有有限组互素的x,y,z满足x^n + y^n = z^n ,这对费马大定理作出重要贡献。
1984年
布兰吉(Louis de Brange)解决了比贝伯猜想。
1984年
沃恩·琼斯(Vaughan Jones)发现了3维球面中纽结和链的一个新多项式不变量。
1984年
威腾(Witten)出版了《超对称与莫尔斯理论》(Supersymmetry and Morse theory),包含了在微分几何研究中具有核心重要性的思想。
1986年
马古利斯(Margulis)证明了关于不定无理二次型在整点的值的“奥本海默猜想”。
1987年
泽尔曼诺夫(Zelmanov)证明了关于一个无穷维李代数何时为幂零的重要猜想。
1988年
朗兰兹(Langlands)是第一个获得美国国家科学院数学奖的人。他获奖是由于“将群表示论带入到与自守形式理论和数论的革命性新关系的非凡远见”。
1988年
艾尔基斯(Elkies)找到了欧拉猜想在n=4的一个反例,即2682440^4 + 15365639^4 + 18796760^4 = 20615673^4.。其后同年弗莱斯(Frye)找到了一个最小反例:95800^4 + 217519^4 + 414560^4 = 422481^4。
1989年
布尔甘(Bourgain)使用分析与概率方法解决了L(p)问题,这是在巴拿赫空间理论与调和分析中为时已久的问题。
1990年
德林菲尔德(Drinfeld)由于在量子群以及数论的工作在日本京都的国际数学家大会获得了菲尔兹奖。
1991年
泽尔曼诺夫(Zelmanov)解决了群论的有限制的伯恩赛德问题。
1991年
王秋冬(Quidong Wang)找到了n体问题的无穷级数解(除了少量例外)。
1993年
梅纳斯科(Menasco)与斯莱维(Thistlethwaite)证明了纽结理论的猜想“泰特第二猜想”,即同一个素纽结的两个约化交错图由一个扭转序列关联。
1994年
怀尔斯(Wiles)证明了费马大定理。
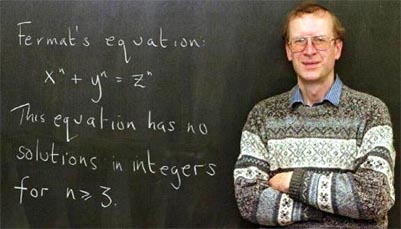
1994年
孔涅(Connes)出版了关于非交换几何的重要教科书。
1994年
利翁(Lions)由于他在非线性偏微分方程的工作获得菲尔兹奖。
1994年
约克斯(Yoccoz)由于他在动力系统的工作获得菲尔兹奖。
1994年
克里斯蒂娜·古皮尔堡(Krystyna Kuperberg)解决了关于动力系统拓扑的“塞夫特猜想”。
1995年
银行家安德鲁·比尔提供大奖悬赏求解比尔猜想:对p, q, r > 2以及互素整数x, y, z,方程x^p + y^q = z^r 无解。
1997年
怀尔斯由于解决了费马大定理获得沃尔夫斯凯尔奖。
1998年
博赫兹(Borcherds)由于在自守形式与数学物理的工作获得菲尔兹奖;高尔斯(Gowers)由于泛函分析与组合数学的工作获奖;孔采维奇(Kontsevich)由于代数几何、代数拓扑与数学物理的工作获奖;麦克马伦(McMullen)由于全纯动力系统与3维流形几何的工作获奖。
1998年
托马斯·黑尔斯(Thomas Hales)证明了关于最密堆积的开普勒问题。
1999年
互联网梅森素数大搜索项目(GIMPS)找到第38个梅森素数:2^6972593 -1。
1999年
康拉德(Conrad)与泰勒(Taylor)证明了“谷山-志村猜想”。怀尔斯在1993年解决费马大定理的途中证明了其中一个特殊情形。
2000年
在洛杉矶举行的美国数学会的一个会议上提出了“21世纪的数学挑战”。不同于100年前的“希尔伯特问题”,这次的问题由30位数学家的团队给出,其中8位是菲尔兹奖得主。
2000年
一个700万美元的大奖被设立来求解七个著名数学难题。称为千禧年大奖难题:P vs NP;霍奇猜想;庞家莱猜想;黎曼假设;杨-米尔斯规范场的存在性与质量缺口;纳维-斯托克斯方程解的存在性与光滑性;贝赫和斯维纳通-戴尔猜想。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Jamie Condliffe。
翻译作者,ALIMJAN,哆嗒数学网翻译组成员。
校对,donkeycn。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
这就是傅里叶变换。你得感激它,因为帮你每天从网上下载音乐的、把图片压缩成很小的JPG文件的、甚至提高耳机消除噪声能力的都是它。下面介绍一下它的原理。
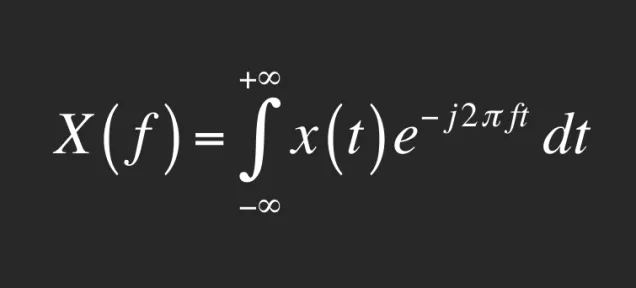
此公式的威力在于它能够使数学家快速掌握任何一种信号的频谱。这一点是相当牛的。但别以为只有我是这么认为的,早在1867年,物理学家开尔文勋爵也表达过自己对傅里叶分析爱慕至极。他写道:“傅里叶定理不仅是现代分析学里的最美的结论之一,而且也许可以说它充当了几乎破解任何晦涩的物理奥秘的必不可少的工具。”而且,至今仍是如此。
数学会将把我们分解
毫无疑问,傅里叶变换是数学家让·巴普蒂斯·约瑟夫·傅里叶男爵(Baron Jean Baptiste Joseph Fourier,1768-1830)创立的,并发表于他1822年出版的《热的解析理论》一书中。他对热如何在物体内部及其附近流动感兴趣,并在研究此现象的过程中推导出了傅里叶变换。当初,他自己并没意识到他的发现是何等重要的贡献——傅里叶变换不仅在数学和物理领域,而且在整个科学,工程和技术领域都是重要的发现。
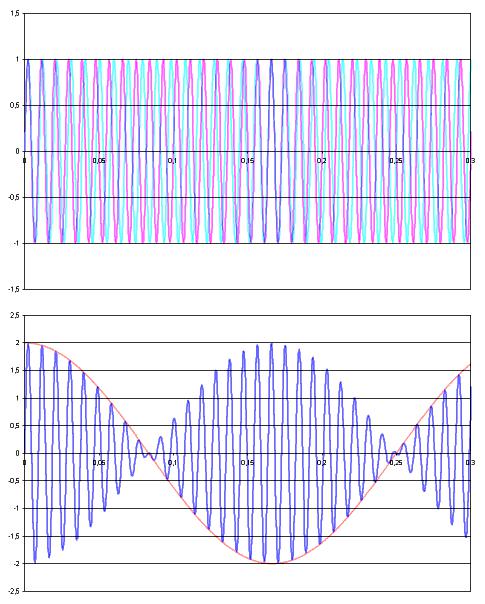
他的主要突破性结果在于他意识到复杂的信号可以简单地表示为一系列简单得多的信号的叠加。他选择用来叠加的正是你在高中学到的、在最大值与最小值之间来回震荡的、规律可预测的正弦曲线。比如,当你同时按下钢琴的三个键时,你会产生三种不同的音符,其中每个都有确定的频率——我们在谈声音的时候指的是音高——这恰似标准的正弦波:
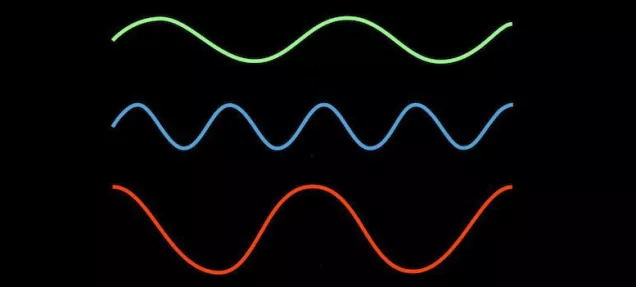
然而,一旦把它们叠加起来以后,原来那悦耳的和弦音听起来就比较杂乱,就像这个:
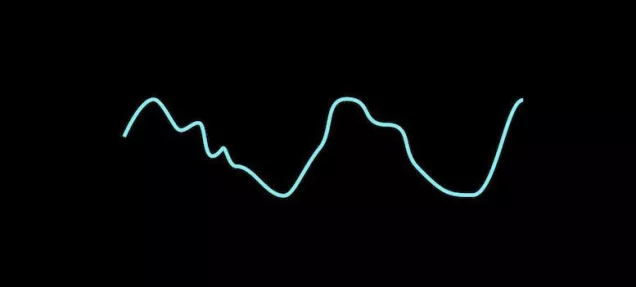
它看起来很复杂,但是我们知道本质上它只是同时把三个普通的正弦波叠加在一起。傅里叶的灵感在于他发现:无论一种波的最终形式有多么复杂,都可以用正弦波的组合叠加来描述——哪怕这意味着这可能需要使用无穷多个正弦波。我觉得这个发现的真正高明之处在于:若你知道为了得到最终的波形来代表信号,你需要知道叠加哪些正弦波,那么你也就可以精确地知道你需要叠加哪些频率的波以及每个波相应的特性。凭借这些知识,你就能精确地知道你叠加出来的最终的信号的频谱。
这些是本篇刚开始介绍的那个公式一下子就能做的事情。x(t) 这一项代表你想通过简单的信号的叠加来表示的那个最初的棘手复杂的信号,e^j2πft这一项看起来有点吓人,但是它只是数学家们用来代表我们以上说的正弦曲线的一个简略表达方式。绝妙的是,把这两项相乘然后整体扔进一个积分运算——前面的那个弯曲的符号以及后面的dt——这个运算能算出每一个参与组成最终信号必需的所有正弦曲线的频率。因此,公式的值X(f),可以得出每一个需要参与叠加的简单分信号的强度和延迟。
这就是傅里叶变换:它的作用是能精确地揭示原始信号包含着哪些频率。这也许听起来微不足道,然而并不是。
传输
如果你要把你录制的歌放在网上,你可以只是按本来录制的原始大小的文件放上去,但那样的话,文件实在是太大了。这是因为,录制过程是个全程无损的:每一个频率在录制、混音至最后完成都会被保留。然而,如果拿一小段音频用傅里叶变换,你就会发现其中某些频率是很显著的而某些频率几乎不存在。
MP3格式的文件就是运用这个原理,只是它通过抛弃那些我们难以察觉的、或者是超出我们听觉范围上限的频率成分来节约空间,因为我们终归还是无法辨别出它们。整个过程都是如此,即把一首歌分割成上百万个小段,分离出重要的而抛弃那些无关紧要的频率。最终剩下的都是能够给在耳朵精准的播放出原音频效果的那些最重要的频率或音符。当然了,其文件大小要小于原来的十分之一。
这也跟Spotify的桌面客户端采用的Ogg Vorbis 格式的工作原理非常相似。(实际上,Vorbis采用的是傅里叶变换的快速计算版本:离散余弦变换,但其本质大略相同。)顺便说一下,Shazam也是运用类似的原理,它有着一个拥有不同歌曲频谱的数据库用于与你正在播放的歌曲的频谱比对,因为这要比直接比对两首歌曲要更可靠。就音频而言,你所戴的降噪耳机同样也是依靠傅里叶变换:有一个麦克风会记录你周围的噪音,得出其全部频谱,然后叠加与这些噪音相同频率、但位相相反的波到你的音乐中从而将类似于婴儿哭声或马路噪声之类的噪音清除。
当然傅里叶公式并非只有这一个技能。我们目前只谈到音频这种时间信号,当初傅里叶创立它是为了解决物体之间的热流问题。这表明,傅里叶公式也可以用来处理关于空间的问题。对于傅里叶而言,这意味着在二维平面内通过叠加一些简单的热流来表示复杂得多的热流。以十分相似的方式,傅里叶变换也可以比一个像素一个像素的处理方式更有效地来创建数字图像。
无损的彩色图像文件的每一个像素都有它独特的颜色。当你以JPG格式存一个图片时,整个图片被分割成许多小块,并且在每个小块都进行二维傅里叶变换。它提供了在每一小块上颜色和亮度如何变化的空间频率的描述。类似于处理MP3格式的文件那样,JPG抛弃了一些能使图像画质更高的高频的成分。然而,对于大部分人来说,人眼毕竟区分不出相近的颜色之间的一些微妙差异,因此抛弃那些高频部分后所导致的一个像素一个像素的变化,人眼几乎是看不出来的。显然,你如果继续压缩,开始抛弃越来越低频的成分时,图片会出现块效应,即在块与块的边界处颜色的变化会很明显。
除了那些拥有最训练有素的眼睛、耳朵的那些人,在多数情况下,类似MP3,JPG等的压缩文件是几乎不可察觉出和压缩前有何区别的。它们看起来、听起来都特别逼真而且占用空间比它们那些无损的版本来说是微不足道的。换言之,压缩让数字音乐和数字图像变得可行,使得我们更容易地分享。这一切都是一个公式的绝对惊人的妙处。毋庸置疑,写了热流理论书的傅里叶会赞成的。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
根据邵逸夫奖5月14日官网消息,2018年度邵逸夫数学奖已经公布。美国数学家,来自美国德克萨斯大学奥斯汀分校数学教授路易·卡法雷 (Luis A Caffarelli)获得此奖项。"以表彰他在偏微分方程上的突破性工作,包括创立一套正则理论,适用于如 蒙日−安培方程等非线性方程,及如障碍问题等的自由边界问题,这些工作影响了该领域整个世代的研究。"

路易·卡法雷在数学界被视为自由边界问题和非线性偏微分方程方面的顶级专家。在2012年,卡法雷还得到过另外一个重要的数学奖项——沃尔夫数学奖。
此次邵逸夫奖的颁奖典礼将于2018年9月26日(星期三)于香港举行。

“邵逸夫奖”是按邵逸夫先生的意愿在2002年成立,以表彰在学术及科学研究或应用上在近期获得突破性的成果,和该成果对人类生活产生深远影响的科学家,原则是不论得奖者的种族、国籍、性别和宗教信仰。
“邵逸夫奖”有三个奖项,分别为:天文学、生命科学与医学、数学科学。每年颁奖一次,每项奖金一百二十万美元。
“邵逸夫奖”被不少人誉为“东方诺贝尔奖”。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
世界数学家大会(International Congress of Mathematicians,简称ICM)是世界上最重要的数学会议。因为这个大会每四年举办一届,所以有着“数学界的奥运会”的别称。这个会议会讨论世界上最前沿的数学学术问题,也会有各种普及讲座推广数学。另外,被认为数学最高荣誉,有着“数学界的诺贝尔奖”的菲尔兹奖,也是在这个会议上办法的。

2018年又是世界数学家大会的举办年份。此次世界数学家大会将在巴西最大的港口城市里约热内卢召开。大会组织方精心录制了一个大约3分钟左右宣传视频,欢迎大家来参会。
视频虽然短小,但内容丰富。大致介绍了城市的概况和发展、城市的活动组织经验(奥运会、世界杯)、巴西组织的数学活动(数学文化节、奥数竞赛)、会场准备情况、会场周边配套和交通状况以及大会的会议内容。
欢迎欣赏。enjoy!
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

“在我看来,在传统的人类审查与计算机验证之间的选择,就像科学上在日晷与原子钟之间的选择一样。”——汤姆·海耶斯(Tom Hales, 参见 [4])

“由于计算机与人是非常不同的,计算机的快速进展促使这点发生了戏剧性的变化。例如,阿佩尔(Appel) 与哈肯(Haken)使用了巨量的自动运算完成了四色定理的证明,引起了大量的争论。在我看来,这些争论几乎不涉及到人们对定理的真实性或者证明的正确性。这反映出了,除了对‘定理是正确的’这种知识以外,人类还想要理解定理,这是一种持续的欲望。” ——比尔·瑟斯顿( Bill Thurston,参见[6])
一个机器检验的证明(machine-checked proof)是在叫做“证明助手”(proof assistant)的软件中撰写的证明。这个证明助手保证了撰写的明证之于“数学公理”与“逻辑规则”是可以编译的。在定理证明中使用计算机的影响是两极化的。关于这个话题,上面的引用代表了涉及到这个主题的一些观点。
1.到底什么是计算机辅助证明?
2.使用计算机来证明定理有什么长处与缺点?
3.对证明助手的学习使用有兴趣的人,应该如何起步呢?
动机的问题
计算机辅助的证明是一门技术。当时使用旧技术不能解决一些问题的时候,数学家就会关心新技术。这就是我们的动机的问题:

我们来看两个已经解决了的问题。第一个是魔方。第二个是安德鲁·怀尔斯(Andrew Wiles)作出的费马大定理的证明。
证明丢番图方程与解魔方之间有一个很大的差别:当一个人解决了魔方的问题,他立即知道问题解决了,然而怀尔斯的证明花费了几个月的时间来进行正式的审查。
随着我们数学教育阶段的提升。我们检查答案的能力在下降。比如,我的启蒙数学课是我母亲教我的数数。就比较小的加法来说,我可以使用数手指的办法来检查我的答案。从一到十的基本数字以及用手指验证答案都是母亲教会我的。一个人学会了解代数方程,也就学会了使用变量代换来检查答案。检查微积分就更加的棘手了,我们尚可以对Wolfram Alpha报以比较大的信心(译者注,Wolfram Alpha是一个数学软件,可以做符号运算。具有计算积分的功能,还能告诉你得到答案的步骤)。至于实分析与抽象代数,学生们最终是把作业交给老师,看看教授们是否相信他们的论证,这样来检查他们的作业正确与否的。
什么是证明助手?
一个计算机证明助手可以对数学论证做更加系统化的检查。用户使用半形式化的语言(既不像形式逻辑那么形式化,也不像日常数学那么非形式化)来撰写他们的证明。证明助手基于某些数学基础来检查证明。正常情况下,我们想起数学基础,我们想到的是集合论。然后由于技术的原因,证明助手是就“类型论”的基础来实现的。在提出ZFC集合论的大致同时,罗素与怀特海提出了类型论作为另一个数学基础。有不同的数学基础,这在哲学上产生了不同的影响。对于我们来说,这是有争议的,我们在这个问题上就此打住。
下图展示了证明助手Lean中的一个正确的证明与一个不正确的证明:

红色错误信息已经很清楚地显示了上面的证明是错误的。下面的证明,由于没有错误,可以迅速看出是正确的。就像魔方一样,一个证明是否正确可以很清楚的看出来。
这看起来有点复杂。这是必须的吗?可能是。比如,海耶斯的开普勒定理的证明由于太复杂而不能让期刊编辑来检查。那个证明最终是用证明助手HOL-light来检查的。那个形式化地验证开普勒猜想的计划叫做Flyspeck计划。Flyspeck花费了几年数年时间与微软Azure Cloud 五千个处理器小时才完成。一些人期望一个不那么重度依赖于计算机的证明,以便数学家可以阅读那个证明。
乔治·贡蒂尔(Georges Gonthier)及其微软研究院的同事作出了第一个经过形式验证的四色定理的证明。这个不同于那个最开始的基于计算机的四色定理的证明。本质上,那个原始的证明是拥有非常大量的计算机计算的标准数学论证。贡蒂尔的工作审查了这一点:支撑四色定理证明的算法,事实上,做了我们相信它做的。
费特-汤普森奇阶定理(Feit-Thompson odd order theorem),是有限单群分类的基石。贡蒂尔的团队使用证明助手Coq形式证明了它。费特-汤普森奇阶定理的原始论文有255页。这个团队其它被高关注度的项目还包括素数定理、哥德尔不完全定理以及中心极限定理的形式证明。
如何起步?
这些工具并不是只能用于那种耗费数年的大规模的证明。也存在一些库包含了如下学科的定理与定义:实分析、一般拓扑学、表示论与抽象代数。在工业界,证明助手也用于验证软件与算法。这是非常强大的。一旦一个人可以用数学上严格的方式来宣称“这个程序P没有缺陷(bug)”,他就能证明这件事。利用形式证明软件,程序员可以确信他们的程序是没有错误的。
市面上有很多证明助手软件供人使用。它们都是免费的。
Isabelle-HOL是劳伦斯·保尔森(Lawrence Paulson)编写的一个证明助手。它基于高阶逻辑。Isabelle 拥有大量可以使用的库以及一些强大的"自动化技术"。这里自动化技术指的是证明助手能为你自动找出一些比较短的证明。HOL-Light是约翰·哈里森(John Harrison)所写、拥有更小的内核的类似程序。
Coq 与Lean都基于依赖类型论。开发它们的团队分别被蒂埃里·科康(Thierry Coquand) 与 里奥·德·莫拉(Leo de Moura)所带领。依赖类型论意味着数据类型可以依赖于其它数据类型——这正是我们所希望的。例如,对于任意的k, 我们希望有这么一个类型Fin(k),它是成员基数为k的有限集合。这些证明助手,即使是近期发布的,自动化能力也较弱;由于技术原因,在依赖类型论中实现自动化,是更困难的办法(至少目前是这样)。
上面提到的证明助手都有在线手册。Lean 2有一个交互式的网页版教程(https://leanprover.github.io/tutorial/)。Lean的当前版本号是3,不过笔者发现阅读这个教程是总体上品味证明助手思想的好方式。
问题与展望
对于一线数学家来说,证明助手当前还没有好到可以让他们自如的使用的地步。海耶斯确实在他的开普勒问题的工作中使用了HOL-light,不过,除非数学家迫不得已,他们是不愿意做这样类似的事情的。当前的库,还没有足够大到包括关于日常定理的日常论证。例如,我们本来想证明一个关于紧李群的标准结论,发现哈尔定理(Haar’s theorem,证明哈尔测度存在性的)不在我们的库里。这个定理经常被引用,它的证明冗长,而且,就当前的技术来说,得到我们希望的那种形式证明还需要花费数年时间。
还有另一个更加本源的反对理由。用瑟斯顿的语言来说,数学,最终是关于数学对象的理解,防止我们的理解走入迷途的证明仅仅是第二位的。用伟大的组合学家罗塔(G.-C. Rota)的话说,“说一个数学家‘证明了定理’就像是说一个作家‘写了一串单词’一样”。他的意思是,算法化的“证明搜索”那种形式的论证不是我们所想要的。
不过,并没有什么证据表明,一个人理解数学对象与使用计算机证明助手是相冲突的。机器检验并不是证明搜索的同义词。当前,期刊有人类审查员来检查细节的技术性的论证。如果能够使用计算机来检查这些,我们损失任何东西,反而得到了更多的可核查性。
史蒂芬·沃尔弗拉姆(Steven Wolfram)最近对形式证明产生了兴趣。沃尔弗拉姆的团队已经在努力工作以使Mathematica与形式证明合作[1]。相关的语言学家、计算机科学家以及数学家时常在考虑那些让计算机代码看起来更像日常数学的方法。最终目标是提高审查过程的效率。
所有的期刊都要求我们使用LaTeX来写论文——虽然并不一直如此。也许在未来,一些期刊将会为了计算机检查而要求半形式化语言的证明。那样,期刊编辑将把更多注意力放在清晰性以及数学文章的总体展示上面——这就是加深了人类对数学的理解。
致谢
我对卡耐基梅隆大学的杰里米·阿维加德(Jeremy Avigad)和匹斯堡大学的汤姆·海耶斯(Tom Hales)致以最大的感激,是他们教会我我所知道的关于证明助手的知识。 我同样对约翰霍普金斯大学的艾米利·里尔(Emily Riehl)表示感谢,是他让我知道了比尔·瑟斯顿(Bill Thurston)的《论证明与数学的进展》(On Proof and Progress in Mathematics)。这篇杰出的文章,我在本文中引用了多次。最后,我把这个笔记献给晚年的弗拉基米尔·沃沃斯基(Vladimir Voevodsky)。我个人从未见过他,不过,他给我的多位老师的影响,他的论文,他的讲稿记录,都是我的本科教育中最重要的东西。
原参考文献
[1] Geuvers, H., England, M., Hasan, O., Rabe, F., Teschke, O. Intelligent Computer Mathematics, 10th International Conference, CICM 2017, Edinburgh, UK, July 17-21, 2017, Proceedings.
[2] Gonthier, G.: Formal proof—the Four Color Theorem. Notices of the AMS 55(11), 1382–1393 (2008)
[3] Georges Gonthier, Andrea Asperti, Jeremy Avigad, Yves Bertot, Cyril Cohen, Fran¸cois Garillot, Stéphane Le Roux, Assia Mahboubi, Russell O’Connor, Sidi Ould Biha, Ioana Pasca, Laurence Rideau, Alexey Solovyev, Enrico Tassi, and Laurent Théry, A machine-checked proof of the odd order theorem, Interactive Theorem Proving – 4th International Conference, ITP 2013, Rennes, France, July 22-26, 2013. Proceedings (Sandrine Blazy, Christine Paulin-Mohring, and David Pichardie, eds.), Lecture Notes in Computer Science, vol. 7998, Springer, 2013, pp. 163–179.
[4] Hales, T., & Hales, T. C. (2012). Dense sphere packings: a blueprint for formal proofs (Vol. 400). Cambridge University Press.
[5] Hales, T.C. Introduction to the Flyspeck project. In Thierry Coquand, Henri Lombardi, and Marie-Franc¸oise Roy, editors, Mathematics, Algorithms, Proofs, number 05021 in Dagstuhl Seminar Proceedings, Dagstuhl, Germany, 2006. Internationales Begegnungs- und Forschungszentrum f¨ur Informatik (IBFI), Schloss Dagstuhl, Germany. http://drops.dagstuhl.de/opus/volltexte/2006/432.
[6] Thurston, W.: 1994, ‘On Proof and Progress in Mathematics’, Bulletin of the American Mathematical Society 30(2), 161–177.
原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 数学上下三万年(六):十九世纪下半叶的数学
人类历史上第一次世界大战和第二次世界大战在这一时期发生,战争催生了科技进步,同时数学也向两个完全不同的方向发展——与现实需求结合的应用数学,以及更加理论化抽象化的基础数学。这段时间数学界大师辈出,重要的历史节点不断。而中国进入民国时期,现代大学制度开始确立。知识界开始宣扬引进“德先生”和“赛先生”。这个时期,中国也催生不少大师。
本期出场人物有:希尔伯特、罗素、普朗克、勒贝格、哈代、爱因斯坦、庞加莱、外尔、凯恩斯、巴拿赫、谢尔宾斯基、塔尔斯基、科尔莫戈诺夫、布劳威尔、豪斯道夫、怀特海、诺特、阿廷、冯诺依曼、图灵、哥德尔、香农、丘奇、韦伊、维纳。
本系列下面是往期内容:
1900年
希尔伯特在巴黎的第二届国际数学家大会上提出了23个问题作为20世纪的挑战。这些问题包括连续统假设、实数的良序化、哥德巴赫猜想、代数数的幂的超越性、黎曼猜想、“狄利克雷原理”的扩展等等。大部分问题在20世纪得到解决,每一个问题的解决都是数学界的一个重要事件。

1900年
古尔萨(Goursat)出版《数学分析教程》(Cours d'analyse mathematique),引入了许多新的分析概念。
1900年
弗雷德霍姆(Fredholm)在《求解狄利克雷问题的新方法》(Sur une nouvelle méthode pour la résolution du problème de Dirichlet)中发展了他的积分方程理论。
1900年
费耶(Fejér)发表了傅立叶级数的一个基本求和定理。
1900年
列维-齐维塔(Levi-Civita)和里奇-库尔巴斯托罗(Ricci-Curbastro)出版了《绝对微积分方法及其应用》(Méthodes de calcul differential absolu et leures applications),其中他们建立了张量理论,15年后在广义相对论中用到。
1901年
罗素(Russell)发现了“罗素悖论”,用一种简单的方式说明了朴素集合论固有的问题。
1901年
普朗克(Planck)提出了量子理论。
1901年
求常微分方程数值解的龙格库塔法(Runge-Kutta method)被提出。
1901年
勒贝格(Lebesgue)阐述了测度论。
1901年
迪克逊(Dickson)出版了《线性群并述伽罗瓦理论》(Linear groups with an exposition of the Galois field theory)。
1902年
勒贝格给出了“勒贝格积分”的定义。
1902年
巴普·利维(Beppo Levi)第一次提出了选择公里。
1902年
吉布斯(Gibbs)出版了《统计力学基本原理》(Elementary Principles of Statistical Mechanics),这份漂亮的描述将统计力学建立在坚实的基础上。
1903年
卡斯泰尔诺沃(Castelnuovo)出版了《解析与射影几何》(Geometria analitica e proiettiva),这是他在代数几何的最重要的著作。
1904年
策梅洛(Zermelo)利用选择公理证明每个集合可以被良序化。
1904年
洛仑兹(Lorentz)引入了“洛仑兹变换”。
1904年
庞加莱提出庞加莱猜想:每个同伦等价于3维球面的3维闭流形必定是3维球面。
1904年
庞加莱在一个讲座中提出一种相对性理论来解释迈克尔逊-莫雷实验。
1905年
爱因斯坦(Einstein)发表了狭义相对论。
1905年
拉斯克(Lasker)证明了多项式环理想分解为准素理想的分解定理。
1906年
弗雷歇(Fréchet)在他的博士论文研究了度量空间的泛函,描述了紧致性的抽象概念。
1906年
马尔可夫(Markov)研究了随机过程,后被称为“马尔可夫链”。
1906年
贝特曼(Bateman)将拉普拉斯变换应用于积分方程。
1906年
科赫(Koch)发表了《平面曲线理论若干问题研究的初等方法》(Une methode geometrique elementaire pour l'etude de certaines questions de la theorie des courbes plane),其中包含了“科赫曲线”。它是一条具有无穷长度且处处不可微的连续曲线。
1907年
弗雷歇(Fréchet)发现了关于“平方勒贝格可积函数”空间上的泛函的积分表示定理。里斯(Riesz)独立地发现了相似的结果。
1907年
爱因斯坦发表了他的等效原理,即重力加速度与机械力的加速度是无区别的。它是广义相对论的关键组成部分。
1907年
希加德(Heegaard)和德恩(Dehn)出版了《位置分析》(Analysis Situs),标志了组合拓扑学的开端。
1907年
布劳威尔(Brouwer)关于数学基础的博士论文对数学的逻辑基础提出了挑战,标志了直觉主义流派的开端。
1907年
德恩(Dehn)对于群表示提出了字问题和同构问题。
1907年
里斯(Riesz)证明了关于希尔伯特空间上傅立叶分析的“里斯-费舍尔定理”。
1908年
戈塞(Gosset)引入“学生t检验”来处理小样本。
1908年
哈代(Hardy)和温伯格(Weinberg)提出了一个定律来描述显性遗传特征和隐性遗传特征在一个群体中如何传播。奠定了群体遗传学的数学基础。
1908年
策梅洛(Zermelo)出版了《论集合论基础》(Untersuchungen über die Grundlagen der Mengenlehre)。他把集合论建立在七个公理上:外延公理,基本集合公理,分离公理,幂集公理,并集公理,选择公理和无穷公理。旨在克服康托尔遇到的集合论困难。
1908年
庞加莱出版了《科学与方法》(Science et méthode),这也许是他最著名的大众读物。
1909年
卡迈克尔(Carmichael)研究伪素数。
1909年
爱德蒙·兰道(Edmund Landau)给出了解析数论的第一个系统介绍。
1910年
罗素(Russell)和怀特海(Whitehead)出版了《数学原理》(Principia Mathematica)的第一卷。他们试图将整个数学建立在逻辑基础上。他们能够提供集合论、有限和超限算术、和基本测度论主要定理的详细推导。最后第三卷在三年后出版,而计划中关于几何的第四卷没有完成。
1910年
斯坦尼茨(Steinitz)在《域的代数理论》(Algebraische Theorie der Körper)给出了域的第一个抽象定义。
1911年
谢尔盖·伯恩斯坦(Sergi Bernstein)在对魏尔斯特拉斯1885年一个定理的构造性证明中引入了“伯恩斯坦多项式”。
1912年
当儒瓦(Denjoy)引入了“当儒瓦积分”。
1913年
哈代(Hardy)收到了拉玛努金(Ramanujan)的信。他把拉玛努金带到剑桥,他们共同写了5篇卓越的数论论文。

1913年
外尔(Weyl)出版了《黎曼曲面概念》(Die Idee der Riemannschen Flache),把分析、几何与拓扑连接在一起。
1914年
豪斯道夫(Hausdorff)出版了《集合论的要点》(Grundzüge der Mengenlehre),其中他创建了一种拓扑度量空间的理论。
1914年
比伯巴哈(Bieberbach)引入了“比伯巴哈多项式”,用于逼近将给定单连通区域共形映射到圆盘的函数。
1914年
哈那德·玻尔(Harald Bohr)与爱德蒙·兰道(Edmund Landau)证明了关于ζ函数的零点分布的定理。
1915年
爱因斯坦提交了一篇论文,给出了广义相对论的定稿。
1916年
比伯巴哈(Bieberbach)提出了比伯巴哈猜想。
1916年
麦考利(Macaulay)出版了《模系统的代数理论》(The algebraic theory of modular systems),研究了多项式环的理想。它包含了很多出现在“Grobner基”理论中的思想。
1916年
谢尔宾斯基(Sierpinski)给出了第一个绝对正规数的例子,这种数在任何基底下每个数字出现机会均等。
1917年
挂谷宗一(Kakeya)提出了关于最小面积的问题。
1919年
罗素(Russell)出版了《数学哲学引论》(Introduction to Mathematical Philosophy),大部分在罗素因反战活动入狱时在狱中写成。
1919年
豪斯道夫(Hausdorff)引入了“豪斯道夫维数”的概念,它是一个物体的拓扑维数与3之间的一个实数。它被用于研究例如科赫曲线这样的对象。
1920年
高木贞治(Takagi)发表了关于类域论的基础性论文。
1920年
哈塞(Hasse)发现了“局部-整体”原理。
1920年
西格尔(Siegel)的论文在丢番图逼近理论上有重要地位。
1920年
谢尔宾斯基(Sierpinski)和马祖尔克维奇(Mazurkiewicz)创立了《数学基础》(Fundamenta Mathematicae)。
1921年
凯恩斯发表了他的《论概率》(Treatise on Probability),他认为概率是一个逻辑关系,因此是客观的。涉及概率关系的命题具有独立于人们意见的真值。这对统计和经济都有深远的影响。
1921年
费希尔(Fisher)将似然性概念引入到统计学。
1921年
博雷尔(Borel)发表了一系列关于博弈论的论文,他成为第一个定义策略博弈的人。
1921年
埃米·诺特(Emmy Noether)出版了《环中的理想论》(Idealtheorie in Ringbereichen),这在现代抽象代数学有根本重要性。
1922年
理查森(Richardson)出版了《通过数值过程预报天气》(Weather Prediction by Numerical Process)。他是第一个将数学方法,特别是有限差分法,用于预测天气的人。手算的计算让人望而却步,只有计算机的发展让他的想法得以实现。
1922年
巴拿赫(Banach)由于一篇关于测度论的论文而获得讲师资格。他开始了关于赋范向量空间的工作。
1922年
弗兰克尔(Fraenkel)试图将集合论建立在公理化基础上。
1922年
切博塔廖夫(Chebotaryov)证明了关于算术级数中素数密度的定理。
1922年
费耶(Fejér)和里斯(Riesz)发表了关于共形映射的重要工作。
1922年
柯尔莫哥洛夫(Kolmogorov)构造了一个几乎处处发散的可和函数。
1923年
斯达迪(Study)发表了关于低维实与复代数的重要工作。
1924年
亚历山大(Alexander)引入了著名的“亚历山大带角球”。
1925年,费希尔(Fisher)出版了《研究工作者的统计方法》(Statistical Methods for Research Workers)。他给出用于生物学的实验方法和统计方法。
1925年
怀特海(Whitehead)出版了《科学与当代世界》(Science and the Modern World)。它来源于在美国的一系列讲座,成为他后来的形而上学的导论。他考虑了“科学唯物主义”(自然界只有物质和能量)的成长、成功与影响。
1925年
贝西科维奇(Besicovitvch)解决了关于最小面积的“挂谷问题”。
1925年
克鲁尔(Krull)证明了关于分解阿贝尔算子群的“克鲁尔-斯密特定理”。
1926年
瑞德迈斯特(Reidemeister)出版了关于纽结理论的重要著作《节点和群》(Knoten und gruppen)。
1926年
阿廷(Artin)与施雷尔(Schreier)发表了关于有序化形式实域与实闭域的论文。
1926年
巴拿赫(Banach)与塔斯基(Tarski)在《数学基础》(Fundamenta Mathematicae)上联合发表一篇论文《分解点集为相同的两部分》(Sur la decomposition des ensembles de points en parties respectivement congruentes)发表了“巴拿赫-塔斯基悖论”
1927年
埃米·诺特(Emmy Noether),赫尔姆特·哈塞(Helmut Hasse)和理查·布劳尔(Richard Brauer)开展关于非交换代数的工作。
1927年
阿廷(Artin)在《一般性互反律的证明》(Beweis des allgemeinen Reziprozitätsgesetzes)发表了他的互反律。
1928年
冯·米塞斯(Von Mises)出版了《概率,统计与真相》(Probability, Statistics and Truth)。
1928年
冯·诺依曼(Von Neumann)证明了博弈论的极小极大定理。
1928年
霍普夫(Hopf)引入了同调群。
1929年
格尔丰德(Gelfond)给出了关于有理数域上的代数数的线性独立性的猜想。
1930年
范德瓦尔登(Van der Waerden)出版了重要著作《现代代数学》(Modern Algebra)。这部两卷本著作展示了由诺特、希尔伯特、戴德金和阿廷发展的代数学。
1930年
胡尔维茨(Hurewicz)证明了关于可分度量空间到紧致空间的嵌入定理。
1930年
库拉托斯基(Kuratowski)证明了关于平面图的定理。
1931年
乔治·戴维·伯克霍夫(G D Birkhoff)证明了一般遍历定理。通过使用勒贝格测度,将麦克斯韦-玻尔兹曼气体分子运动理论转变为严格的原理。
1931年
哥德尔(Gödel)发表了《在数学以及相关系统中的形式不可判定命题》(Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme)。他证明了关于公理系统的基础性结果,表明在任何包含算术系统的公理化数学系统中存在不能在公理系统内被证明或证伪的命题。特别地公理的相容性不能被证明。

1931年
冯·米塞斯(Von Mises)将样本空间的思想引入到概率论。
1931年
博苏克(Borsuk)发表了度量微分几何的收缩理论。
1932年
哈尔(Haar)引入了群的“哈尔测度”。
1932年
赫尔(Hall)出版了《具有素数幂阶的群理论的贡献》(A contribution to the theory of groups of prime power order)。
1932年
马格努斯(Magnus)证明了对于单关系群,字问题为真。
1932年
冯·诺依曼(Von Neumann)出版了关于量子力学的《量子力学的数学基础》
1933年
柯尔莫哥洛夫(Kolmogorov)出版了《概率论基础》(Foundations of the Theory of Probability),展示了概率的公理化处理。
1934年
格尔丰德(Gelfond)与施奈德(Schneider)分别独立地证明了和希尔伯特第七问题有关的命题。他们证明了当a是代数数(不等于0和1)且q为无理代数数,a^q为超越数。
1934年
勒雷(Leray)证明纳维-斯托克斯方程弱解的存在性。
1934年
佐恩提出了“佐恩引理”,该引理可能由杜奇(Tukey)命名。它等价于选择公理。
1935年
邱奇(Church)发明了“λ演算”,对于今天的计算机科学家是一件无价的工具。
1936年
图灵(Turing)发表了《论可计算数及其在判定问题上的应用》(On Computable Numbers, with an application to the Entscheidungsproblem),其中描述了一种理论上的机器,现在称为“图灵机”。它成为可计算性理论的重要组成部分。
1936年,邱奇(Church)出版了《初等数论中的一个未解决问题》(An unsolvable problem in elementary number theory)。其中包含了邱奇定理,它表明算术没有判定程序。
1937年,维诺格拉多夫(Vinogradov)出版了《关于素数理论的一些定理》(Some theorems concerning the theory of prime numbers),其中他证明了每个充分大的奇整数可以表为三个素数之和。这是对解答哥德巴赫猜想的重要贡献。
1938年
柯尔莫哥洛夫(Kolmogorov)出版了《概率论中的解析方法》(Analytic Methods in Probability Theory),它为马尔可夫随机过程理论奠定了基础。
1939年
道格拉斯(Douglas)给出了普拉托问题的完整解答,证明了给定一个边界存在一个极小曲面以它为边界。
1939年,亚伯拉罕·艾伯特(Abraham Albert)出版了《代数的结构》(Structure of Algebras)。
1940年
贝尔(Baer)引入了内射模的概念,开始研究几何中的群作用。
1940年
亚历山德罗夫(Aleksandrov)引入正合序列。
1941年
林尼克(Linnik)在数论中引入大筛法。
1941年
亚伯拉罕·艾伯特(Abraham Albert)开始关于非结合代数的工作。
1942年
斯廷罗德(Steenrod)发表了一篇论文,其中首次引入了“斯廷罗德平方”。
1942年
艾伦伯格(Eilenberg)和麦克兰恩(Mac Lane)发表了一篇论文,首次引入了“Hom”与“Ext”。
1943年
马歇尔·赫尔(Marshall Hall)发表了关于射影平面的工作。
1943年
纳依玛克(Naimark)证明了关于希尔伯特空间中算子的自伴代数的“盖尔芳德-纳依玛克定理”。
1944年
冯· 诺伊曼(Von Neumann)和摩根斯坦(Morgenstern)出版了《博弈论与经济行为》(Theory of Games and Economic Behaviour)。博弈论被用于研究经济学。
1944年
阿廷(Artin)研究了满足最小条件的环,现在称为“阿廷环”。
1945年
艾伦伯格(Eilenberg)和麦克兰恩(Mac Lane)引入术语“范畴”和“自然变换”。
1946年
韦伊(Weil)出版了《代数几何基础》(Foundations of Algebraic Geometry)。
1947年
乔治·伯纳德·丹齐格(George Dantzig)引入了最优化问题的单纯形法。
1948年
诺伯特·维纳(Norbert Wiener)出版了《控制论:或关于在动物和机器中控制和通信的科学》(Cybernetics: or, Control and Communication in the Animal and the Machine)。“控制论(cybernetics)”一词来源于维纳。该书详述了关于信息控制理论的工作,特别是应用于计算机。
1948年
香农(Shannon)发明了信息论,并应用数学方法来研究信息传输的误差。这在计算机科学与通信是至关重要的。
1948年
施瓦茨(Schwartz)出版了《函数、微商、傅里叶变换概念的推广及其在数学物理中的应用》(Généralisation de la notion de fonction, de dérivation, de transformation de Fourier et applications mathématiques et physiques),这是他关于广义函数论的第一篇重要出版物。
1949年
莫奇莱(Mauchly)和爱克特(John Eckert)建造了二进制自动计算机(BINAC)。这台机器的一个重要进步是将数据存储在磁带上而不是穿孔卡片。
1949年
塞尔伯格(Selberg)和埃尔德什(Erdös)找到了素数定理的一个不使用复变函数论的初等证明。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,Michael Alba。
翻译作者,donkeycn,哆嗒数学网翻译组成员。
校对,小米。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
许多人会对晦涩的符号以及严格的数学规则望而生畏,一旦看到一个问题中既有数字又有字母,就会很容易放弃。然而,虽然数学有时可能是困难且难以理解的,但它可以证明的结果有时却可以是美丽的、令人难以置信的,或仅仅只是出人意料的。就比如如下这些结果:
10、 四色定理
四色定理最先是由一个叫Francis Guthrie的人在1852年发现的。当时他试图给一幅画有英国所有郡的地图着色(这是在互联网发明之前,根本没有什么工具可以使用)。他发现了一些有趣的东西:只需最多四种颜色,他就能确保任何两个有公共边界的郡都着不同的颜色。Guthrie想知道这个结论是否对所有的地图成立,这个问题成了多年来一直没有解决的数学趣题。
直到1976年(经历了一个多世纪),这个问题终于被Kenneth Appel和Wolfgang Haken解决了。他们的证明相当复杂并且需依赖于计算机。它指出,在任何政区图中(比如说,画有多个国家的地图),对每个国家进行着色,使得着相同颜色的国家不相邻,只需要四种颜色就足够了。
9、 布劳威尔不动点定理

这个定理来自于一个被称为拓扑学的数学分支,是鲁伊兹·布劳威尔发现的。虽然它的专业表述很抽象,但它在现实世界中有许多令人着迷的应用。现在假设我们有一张图片(例如,蒙娜丽莎),然后我们拿来它的一个副本。我们可以对这个副本做任何我们想做的,放大它,缩小它,旋转它,把它揉作一团,等等。布劳威尔不动点定理说,无论我们对那个副本做了什么,只要我们把它放在原始的图片正上方(且副本在原始的图片上的投影不超出原始的图片的范围),副本上必然存在至少一点,使得该点恰好在它所对应的原始图片上的相应点的正上方。这个点可能是蒙娜丽莎的眼睛,耳朵,或微笑的一部分,虽然不知道它究竟是哪个点,但它确实是存在的。
这在三维空间中也是成立的:现在想象我们有一杯静置的水,然后拿起勺子,想怎么搅拌就怎么搅拌,然后再等它完全静止。由布劳威尔不动点定理,将有至少一个水分子,它会恰好位于搅拌前所处于的位置。(哆嗒小编注:意思是这个意思,单用分子举例子,数学角度看,并不严谨。)
8、 罗素悖论

在19、20世纪的世纪之交,很多人着迷于一个被称为集合论(我们将在后面稍加讨论)的新数学分支。简单地说,集合就是放在一起的一堆东西。当时的观点是,任何东西都可以构成一个集合:所有种类的水果构成的集合、所有美国总统构成的集合,这些都是完全有效的。另外,有一点很重要,集合可以包含其它集合(如前面句子:所有集合的集合也是集合)。在1901年,著名数学家伯特兰·罗素意识到这种观点有一个致命缺陷(并因此导致了第三次数学危机),即:并非任何东西都能构成一个集合。
罗素决定对此进行深入研究,并构造了一个集合,其元素为所有的不以自己作为元素的集合。因为所有的水果构成的集合不包含自己作为元素(估且不论西红柿算不算水果),所以它属于罗素构造的那个集合,当然还有许多其它符合该条件的集合。但是罗素构造的那个集合本身又如何呢?如果它不包含自己作为元素,那么按照它的定义,它就应该包含自己。但是等等……现在它确实包含了它自己,所以按照它的定义,我们自然又得把它拿出来。然后,还是按照它的定义,我们现在又必须把它放回去……等等。这一逻辑悖论导致了集合论(它是当今数学最重要的分支之一)的彻底变革。
7、 费马大定理

还记得在学校里学过的毕达哥拉斯定理吗?它是有关于直角三角形的,说的是:直角三角形中,两个较短边的平方和等于最长边的平方(x² + y² = z²)。皮埃尔·德·费马最著名的定理是:如果你将上述方程中的指数2换成任何一个大于2的正整数,那么这一方程就没有正整数解了(例如,x³ + y³ = z³ 没有正整数解)。
正如费马本人所写的:“我发现了一个绝妙的证明,但书旁边的空白太窄了,写不下。”那真是太糟糕了,因为费马早在1637年就提出这个问题,但它在相当长的一段时间内没有被证明。在经历了很长一段时间后,我的意思是,它终于在1995年(在问题被提出了358年之后)由安德鲁·怀尔斯所证明。
6、 末日论

此处可以合理地假设这篇文章的大部分读者都是人类。作为人类,本条目将特别发人深省:数学可以用来推断我们这个物种可能会在什么时候灭绝。无论如何,我们得用上概率。
这个论点(已经存在了大约30年,并且已经被发现或重新发现了好几次)基本上都是在说人类的时间就快到了。一个版本的说法(归功于天体物理学家J. Richard Gott)出奇地简单:如果把人类这一物种完整的存续时间看成是一条人类从出现到灭绝的时间线,那么我们可以来推断我们现在位于该时间线的何处。
因为“现在”这一时刻只不过是我们作为一个物种、在我们存续时间内的一个随机的时刻,因此我们可以认为,我们有95%的概率处于该时间线的中间95%的某处。如果我们现在恰好位于该时间线的前2.5%分位点处,那留给我们人类的时间最长。如果我们现在恰好位于该时间线的前97.5%分位点处,那留给我们人类的时间最短。这就让我们能够给出人类还能存续多久的一个范围估计。Gott认为,有95%的概率,人类将会在从现在开始的5100年后到780万年后之间的某个时刻灭亡。所以,人类啊,该干嘛干嘛去吧,最好是赶紧去看看你的人生目标清单上还剩下些什么。
5、 非欧几何
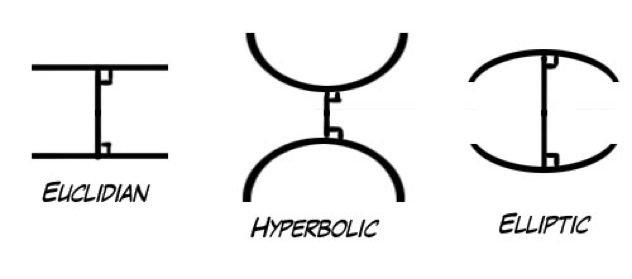
你在学校里学过的、也许还记得的一点点数学大概就是几何了,甚至也就仅仅是你在笔记里随手涂鸦的那些东西。我们大多数人熟悉的几何叫做欧几里得几何,它基于五条相当简单的、不言自明的关于点和线的公理。这些关于点和线的公理很容易在黑板上表示出来,而且很长一段时间,它被认为是几何唯一可行的方法。
然而,问题在于,欧几里得在2000年前提出这些的看似不言自明的真理,并不是在每个人看来都是不言自明的。有一条公理(被称为平行公设)在数学家们看来有点不一样,几个世纪以来许多人试图用其它公理来推导出它。在18世纪初,人们尝试了一种大胆的新方法:于是第五公设(即:平行公设)被简单地替换掉了。然而整个几何体系并没有因此崩溃,反而是产生了一种新的、现在被称为双曲几何(或鲍耶—罗巴切夫斯基几何)的几何。这导致了科学界彻底的范式转变,也为许多不同类型的非欧几何打开了大门。其中比较突出的一个就是黎曼几何,它被用于描述爱因斯坦的相对论(有趣吧,我们的宇宙居然是不遵循欧几里得几何的!)。
4、 欧拉公式
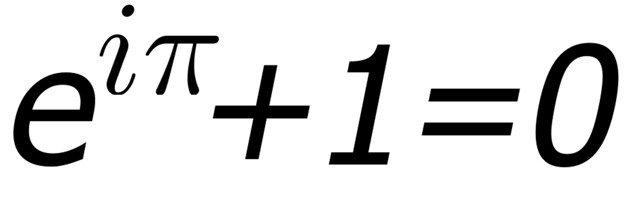
欧拉公式是这篇文章中最强大的结论之一。它归功于史上最多产的数学家之一:莱昂哈德·欧拉。欧拉一生发表了800多篇论文,其中很多是他失明之后发表的。
这个结果乍看起来很简单:e^iπ+1=0。其中e和π都是数学常数,它们经常会出现在各种意想不到的地方,i是虚数单位,它等于-1的平方根。欧拉公式的非凡之处在于:它把数学中最重要的五个数(e,i,π,0和1)组合成了这样一个优美的等式。物理学家理查德·费曼称之为“数学中最神奇的公式”,其重要性在于:它把数学的多个方向统一了起来。
3、 通用图灵机

我们生活在一个由计算机主宰的世界里。也许你现在也恰好是在计算机上读这篇文章!说计算机是二十世纪最重要的发明之一估计也没什么人会反对,然而你可能会惊奇地发现,计算机起源于理论数学的领域。
数学家(同时也是二战时的密码破译者)艾伦·图灵发明了一种被称为图灵机的理论机器。图灵机就像一台非常简单的计算机:它使用无限长的纸带以及3种符号(不妨设为0, 1和空白),然后根据一组指令进行运算。指令可以是:将“0”改为“1”并向左移动一格,或者输入“空白”并向右移动一格(以上只是举例子)。这样,图灵机就可以用来执行任何定义良好的函数运算。
图灵接着描述了什么是通用图灵机,它是一个能够模拟其它所有图灵机的图灵机且能读入任意的输入。这基本上就是存储程序计算机的概念了。图灵仅仅只是用了数学和逻辑,就在技术水平发展到可以设计出真正的计算机之前,创立了计算科学领域。
2、 不同层次的无穷

无穷本身已近是个很难掌握的概念了。人类生就也是很难理解像“无限”这样的概念的。因此,数学家对待无穷一向是谨小慎微的。直到十九世纪下半页,格奥尔格·康托尔才建立了名为集合论(还记不记得我们在罗素悖论那部分曾提到过它?)的数学分支,有了这一理论才能使康托尔能够思索无穷的真正本质。康托尔对无穷的研究成果真是令人叹为观止。
事实证明,对任何一个我们能想象到的无穷,总会存在另一个比我们想象到的那个无穷还要大的无穷。最低层次的那个无穷就是所有正整数(1,2,3…)的个数,这个是可数无穷。随着一些非常优雅的推理,康托尔确认了存在另一个层次的无穷:所有实数(1,1.001,4.1516,…… 包括了你能想到的任何数)的个数。这种类型的无穷是不可数无穷,这意味着即使你拥有宇宙中所有的时间,你也不可能在不漏掉某些实数的情况下按某个顺序列出所有的实数。但是请等一下,按照康托尔的理论,在那个无穷之后还有更多的不可数无穷。那么到底有多少呢?当然是有无穷多个了。
1、 哥德尔不完备定理

在1931年,奥地利数学家库尔特·哥德尔证明的两个定理撼动了整个数学界的核心,因为这两个定理结合在一起给出了让整个数学界沮丧的结论:数学是不完备的,而且永远也不会完备。
技术细节就不赘述了。哥德尔第一不完备定理说的是:对任何形式系统(需包含自然数的系统),总存在该形式系统中的真命题,且该命题在该形式系统内是无法被证明的。然后更本质地,哥德尔第二不完全定理说的是:任何公理体系的无矛盾性都不可能在该公理体系内被证明。永远不会有一个能包含所有数学理论的封闭的系统,因为我们不可能让数学体系完备,所以数学体系只能越来越庞大。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa

原文作者,圣安德鲁斯大学数学与统计学院。
翻译作者,mathyrl,哆嗒数学网翻译组成员。
校对,math001。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
从今天起,我们将连载这部数学编年史。本文是翻译版本,因为工作量巨大,必有疏漏(包括原文也会有错误),欢迎指正。
这应该是网上最全的数学编年史,从公元前30000年到公元2000年,哆嗒数学网为你奉献。
这里是 数学上下三万年(六):十九世纪下半叶的数学
这个时期发生了一些著名的战争或者变革,比如普法战争、美国南北战争、日本明治维新。中国的“师夷制夷” 、“中体西用”的洋务运动也在这个时期内开展。各种科学学科已经很接近于现代,从书写习惯来讲,大部分现代课堂上学到的数学,基本始于这个时代。
本期出场人物有:切比雪夫、波尔查诺、刘维尔、黎曼、哈密顿、布尔、魏尔斯特拉斯、莫比乌斯、戴德金、西罗、吉布斯、埃尔米特、康托、庞加莱、博雷尔、希尔伯特、阿达玛等。
本系列下面是往期内容:
1850年
切比雪夫(Chebyshev)出版了《论素数》(On Primary Numbers),其中他证明了素数理论的新结果。他证明了伯特兰猜想:对于n>1,在n和2n之间至少存在一个素数。
1850年
西尔维斯特(Sylvester)在他的论文《关于一类新的定理》(On a New Class of Theorems)中首次使用了“矩阵”一词。
1851年
波尔查诺的书《无穷的悖论》(Paradoxien des Undendlichen)在他去世三年后出版。该书引入了他的关于无穷集合的想法。
1851年
刘维尔出版了关于特定超越数的存在性的第二本书,这种超越数被称为“刘维尔数”。特别地他给出了一个例子:0.1100010000000000000000010000...,其中在第n! 位为1,其他位为0.
1851年
黎曼(Riemann)的博士论文包含了极其重要的思想,例如“黎曼曲面”及其性质。

1852年
西尔维斯特建立了代数不变量理论。
1852年
古德里(Francis Guthrie)向德摩根提出了四色猜想。
1852年
沙勒(Chasles)出版了《高等几何》(Traité de géométrie),其中讨论了交比、线束(pencils)、对合,这些概念都是他引入的。
1853年
哈密顿出版《四元数讲义》(Lectures on Quaternions)。
1853年
谢克斯(Shanks)计算π到小数点后707位(在1944年人们发现谢克斯从第528位开始算错了)。
1854年
黎曼完成了特许任教资格(Habilitation)。在他的专题论文中他研究了函数用三角级数的可表性。他给出函数可积的条件,被称为“黎曼可积性”。在1854年6月10日发表的演讲《论作为几何基础的假设》(Über die Hypothesen welche der Geometrie zu Grunde liegen)中,他定义了一种n维空间,今天被称为“黎曼空间”。
1854年
布尔初版了《思维规律的研究》(An Investigation of The Laws of Thought on Which are founded the Mathematical Theories of Logic and Probabilities)。他将逻辑归约为代数,被称为布尔代数。
1854年
凯莱第一次尝试定义一个抽象群,虽然没有完全取得成功,但是取得了重要进展。
1855年
麦克斯韦发表了《论法拉第力线》(On Faraday's lines of force),证明只需用几个相对简单的数学方程就可以表示电磁场的行为以及其相互关系。
1856年,魏尔斯特拉斯(Weierstrass)在克雷勒期刊的《阿贝尔函数理论》(Theorie der Abelschen Functionen)中发表了超椭圆积分的反演理论。
1857年,黎曼出版了《阿贝尔函数理论》(Theory of abelian functions)。它进一步发展了黎曼面的思想及其拓扑性质,将多值函数作为一个特殊“黎曼曲面”上的单值函数来研究,并解决了一般的反演问题,这些问题的特殊情形已被阿贝尔和雅可比解决。
1858年
凯莱给出了由西尔维斯特在1850年引入的术语“矩阵”的抽象定义,并在《矩阵理论笔记》(A Memoir on the Theory of Matrices)研究了矩阵的性质。
1858年
莫比乌斯描述了一条只有一个面和一条边的纸带。现在被称为“莫比乌斯带”,它有一个令人惊奇的性质:从中间剪开依然保持完整的一块。利斯廷(Listing)在同一年做出了同样的发现。
1858年
戴德金(Dedekind)发现了一种严格的方法用“戴德金分割”来定义无理数。这个想法是他在思考如何教微积分的时候想到的。
1859年
曼海姆(Mannheim)发明了第一个带有“游标”的现代计算尺。
1859年
黎曼给出了一个有关素数的ζ函数的猜想。尽管在数以百万计的情形下它已被验证是正确的,然而在一般情形下黎曼猜想的正确性仍然未知。它或许是21世纪数学界最著名的未解决问题。
1860年
德劳内(Delaunay)出版了《月球运动理论》(La Théorie du mouvement de la lune)的第一卷,这是他20年的工作成果。他通过给出经度、纬度和月球视差的无穷级数来解决三体问题。
1861年
魏尔斯特拉斯发现了一条处处不可微的连续曲线。
1862年
麦克斯韦提出光是电磁现象。
1862年
杰文斯(Jevons)向英国科学协会讲了《政治经济的一般数学理论》(General Mathematical Theory of Political Economy)。
1862年
利斯廷(Listing)出版了《对欧拉多面体定理推广后的空间几何体研究》(Der Census raumlicher Complexe oder Verallgemeinerung des Euler'schen Satzes von den Polyedern),其中讨论了“欧拉公式”的扩展。
1863年
魏尔斯特拉斯在他的讲座中给出了一个证明:复数是实数的唯一交换代数扩张。
1864年
伯特兰(Bertrand)出版了《论微积分》(Treatise on Differential and Integral Calculus)。
1864年
伦敦数学协会成立。
1864年
本杰明·皮尔斯(Benjamin Peirce)向美国科学会展示了他关于线性结合代数的工作。它利用现代熟知的幂等元和幂零元工具对小于7维的所有复结合代数进行了分类。
1865年
普吕克在几何上做出重要进展,他定义了一种4维空间,其中的基本元素是直线而不是点。
1866年,哈密顿的《四元数原理》(Elements of Quaternions)在他去世后尚未完成,花了7年时间写成的800页手稿在他去世后由他儿子出版。
1867年
莫斯科数学协会成立。
1868年
贝尔特拉米(Beltrami)出版了《非欧几何的一种解释》(Essay on an Interpretation of Non-Euclidean Geometry),其中对罗巴切夫斯基和鲍耶的非欧几何给出了一个具体模型。
1869年
吕罗特(Lueroth)发现了“吕罗特四次曲线”。
1870年
本杰明·皮尔斯(Benjamin Peirce)自费出版了《线性结合代数》(Linear Associative Algebras)。
1871年
贝蒂(Betti)发表了一份拓扑学笔记,其中包含了“贝蒂数”。
1872年
戴德金发表了他对实数的形式构造,并给出整数的一种严格定义。
1872年
海涅(Heine)发表了一篇论文,其中包含了被称为“海涅-博雷尔定理”的定理。
1872年
法国数学协会成立。
1872年
梅雷(Méray)出版了《新无穷小分析》(Nouveau précis d'analyse infinitésimale),致力于通过幂级数展示单复变函数的理论。
1872年
西罗(Sylow)出版了《关于置换群的定理》(Théorèmes sur les groupes de substitutions),其中包含了著名的三个关于有限群的“西罗定理”。他对于置换群证明了这些定理。
1872年
克莱因(Klein)在爱尔兰根发表了就职演讲。他将几何定义为研究一个空间在一个变换群作用下的不变性质。这被称为“爱尔兰根纲领”,深刻地影响了数学发展。
1873年
麦克斯韦出版了《电磁通论》(Electricity and Magnetism)。该书包含了四个偏微分方程,被称为“麦克斯韦方程”。
1873年
埃尔米特(Hermite)出版了《论指数函数》(Sur la fonction exponentielle),其中他证明了e是超越数。
1873年
吉布斯(Gibbs)发表了两篇关于热力学图的重要论文。
1873年
布罗卡尔(Brocard)做出了他的关于三角形的工作。
1874年
康(Cantor)发表了他的第一篇关于集合论的论文。他严格描述了无穷的概念。他证明了无穷有不同的大小。他还证明了一个引起争议的结果:几乎所有的数都是超越数。
1876年
吉布斯(Gibbs)出版了《关于多相物质平衡》(On the Equilibrium of Heterogeneous Substances),它代表了数学在化学中的主要应用。
1877年
康托发现了一个惊奇的事实:区间[0, 1]的点与一个正方形内的点存在一一对应。
1878年
西尔维斯特(Sylvester)成立了《美国数学杂志》。
1879年
肯培(Kempe)发表了他对四色定理的错误证明。
1879年
雷克西斯(Lexis)出版了《统计序列的稳定性理论》(On the theory of the stability of statistical series),开始了时间序列的研究。
1879年
哈尔科夫数学协会成立。
1880年
庞加莱(Poincaré)发表了关于自守函数的重要结果。

1881年
韦恩(Venn)引入了“韦恩图”,它成为集合论的有用工具。
1881年
吉布斯(Gibbs)在为他学生写的小册子中发展了向量分析。这种分析方法在麦克斯韦对电磁波的数学分析中有重要作用。
1882年
林德曼(Lindemann)证明了π是超越数。这就证明了用尺规不可能作出一个正方形使得与给定的圆有相同面积。化圆为方这个古典问题可以追溯到古希腊时期,多个世纪以来成为数学思想发展的驱动力。
1882年
米塔-列夫勒(Mittag-Leffler)建立了《数学学报》(Acta Mathematica)。
1883年
雷诺(Reynolds)出版了《决定水流为直线或曲线运动的条件以及在平行水槽中的阻力定律的探讨》(An experimental investigation of the circumstances which determine whether the motion of water in parallel channels shall be direct or sinuous and of the law of resistance in parallel channels)。书中出现了用于流体力学建模的“雷诺数”。
1883年
庞加莱发表了一篇论文,开启了多复变解析函数理论的研究。
1883年
爱丁堡数学学会成立。
1884年
沃尔泰拉(Volterra)开始了积分方程的研究。
1884年,弗雷格(Frege)出版了《算术基础》(The Foundations of Arithmetic)。
1884年
赫尔德(Hölder)发现了“赫尔德不等式”。
1884年
米塔-列夫勒(Mittag-Leffler)出版了《单变量函数的解析表示》(Sur la représentation analytique fes fonctions monogènes uniformes d'une variable indépendante),给出了他关于指定极点和奇异部分的亚纯函数构造的理论。
1884年
弗罗贝尼乌斯(Frobenius)对于抽象群证明了西罗定理。
1884年
里奇-库尔巴斯托罗(Ricci-Curbastro)开始了关于绝对微积分(absolute differential calculus)的工作。
1884年
巴勒莫数学会(Circolo Matematico di Palermo)成立。
1885年
魏尔斯特拉斯证明实数轴的有限闭区间上的连续函数可以用多项式任意一致逼近。
1885年
埃奇沃斯(Edgeworth)出版了《统计方法》(Methods of Statistics),其中阐述了对于均值比较的显著性检验的应用和解释。
1886年
雷诺阐述了润滑的理论(雷诺润滑方程)。
1886年
皮亚诺(Peano)证明了如果f(x, y)连续,那么一阶微分方程dy/dx = f(x, y)有解。
1887年
列维-齐维塔(Levi-Civita)发表了一篇论文,发展了张量微积分。
1888年
戴德金出版了《数的本质和意义》(Was sind und was sollen die Zahlen)。他将算术建立在严格的基础上,这个基础被称为“皮亚诺公理”。
1888年
高尔顿(Galton)引入了相关系数的概念。
1888年,恩格尔(Engel)和李(Lie)出版了三卷本《变换群理论》(Theorie der Transformationsgruppen)的第一卷,它是关于连续变换群的重要著作。
1889年,皮亚诺(Peano)出版了《算术原理》(Arithmetices principia, nova methodo exposita),通过集合来定义自然数的方式给出了皮亚诺公理,。
1889年
菲茨杰惹(FitzGerald)提出了洛伦兹-斐兹杰惹收缩来解释“迈克耳孙-莫利实验”。
1890年
皮亚诺发现了空间填充曲线。
1890年
圣彼得堡数学学会成立。
1890年
希伍德(Heawood)出版了《地图颜色定理》(Map colour theorems),他指出了肯普(Kempe)对四色定理的证明的错误。他证明了五种颜色是足够的。
1891年
费多洛夫(Fedorov)和申费里斯(Schönflies)独立地对晶体学空间群进行了分类,证明了一共有230 种类。
1892年,庞加莱出版了三卷本《天体力学的新方法》(Les Méthodes nouvelles de la mécanique céleste)的第一卷。他旨在完全刻画机械系统的所有运动,援引流体流动的类比。他还证明,以前例如德劳内(Delaunay)用于研究三体问题的级数展开是收敛的,但一般不是一致收敛。这使人怀疑拉格朗日和拉普拉斯给出的关于太阳系稳定性的证明。
1893年
皮尔逊(Pearson)发表了一系列论文中的第一篇,在此后18年共发表了18篇论文,引入了大量基本概念来研究统计学。这些论文包含了对回归分析和相关系数的贡献,以及对统计显著性的卡方检验。
1894年
庞加莱开始了代数拓扑的工作。
1894年
博雷尔(Borel)引入了“博雷尔测度”。
1894年
嘉当(Cartan)在他的博士论文中对复数域上所有有限维单李代数进行了分类。
1895年
庞加莱出版了《位置分析》(Analysis situs),这是他的第一本拓扑学著作,给出了这个专题的较早的系统性处理。他是代数拓扑的创始人,发表了这个专题的6篇论文。他引入了基本群。
1895年
康托(Cantor)发表了关于超穷算术的两篇重要论文的第一篇。
1895年
安里西·韦伯(Heinrich Weber)出版了他的著名教科书《代数讲义》(Lehrbuch der Algebra)。
1896年
素数定理分别由阿达玛(Hadamard)和法勒布赛(de la Vallée-Poussin)独立地证明。这个定理给出了不超过一个给定数的素数个数的估计,证明了当n趋于无穷时,不超过n的素数个数趋向于n/log n。
1896年
切萨罗(Cesàro)出版了《内蕴几何学教程》(Lezione di geometria intrinseca),其中他阐述了内蕴几何。
1896年
弗罗贝尼乌斯(Frobenius)引入了群特征标。
1897年
亨泽尔(Hensel)发明了p进数(p-adic numbers)。
1897年
布拉利-福尔蒂(Burali-Forti)是第一个发现集合论悖论的人。
1897年
伯恩赛德(Burnside)出版了《有限阶群理论》(The Theory of Groups of Finite Order)。
1897年
弗罗贝尼乌斯开始研究群表示论。
1898年
弗罗贝尼乌斯引入诱导表示的概念以及“弗罗贝尼乌斯互反定理”。
1898年
阿达玛关于负曲率曲面上的测地线的工作为符号动力学奠定基础。
1899年
希尔伯特(Hilbert)出版了《几何基础》(Grundlagen der Geometrie),将几何建立在形式公理之上。

1899年
李亚普诺夫(Lyapunov)提出了方法来决定常微分方程系统的稳定性。
关注微信:哆嗒数学网 每天获得更多数学趣文
新浪微博:http://weibo.com/duodaa
